给定控制数的树的代数连通度

管婷婷

(安庆师范学院 音乐学院，安徽 安庆 246133)



给定控制数的树的代数连通度

管婷婷

(安庆师范学院 音乐学院，安徽 安庆 246133)

摘要：一个图G(V,E)的控制数γ(G)是V的这样一个子集S的最小基数，使得G中每一个顶点或者在S中或者和S中的一些顶点邻接.讨论给定控制数的树的代数连通度,得出树T*=K1，y-1∘K1具有最大的代数连通度；同时利用移接变形刻画出给定控制数2的树中具有最小代数连通度的极图,得出树T=T3(s3,t3)具有最小的代数连通度.

关键词：控制数；树；代数连通度

目前已经有许多文章研究树的拉普拉斯谱半径与图的一些不变量之间的关系.例如:Hong和Zhang[1]研究了给定悬挂点数的树的拉普拉斯谱半径并确定了其中具有最大谱半径的极图;Guo[2]研究了树的拉普拉斯谱半径和直径的关系;冯立华[3]研究了给定控制数的树的拉普拉斯谱半径并且确定了该类树中具有最小谱半径的极图;Guo[4]研究了给定边独立数的树的拉普拉斯谱半径的上界,并刻画出极图.本文将讨论给定控制数的树的代数连通度,刻画出具有最小代数连通度的极图.

1引理

引理2[6]对于树T，有α(T)1,等号成立当且仅当T≅K1,n-1.

引理4[8-9]令e=uv是连通图G的一条割边且G-uv=G1∪G2,|V(Gi)|≥2,(i=1,2),u∈V(G1),v∈V(G2).在G中分离边uv得到图G′,则α(G)α(G′).并且当X(ue)≠0或X(ve)≠0时不等号严格成立,其中X是G′的对应于α(G′)的Fiedler向量.

2主要结论

定理1具有n个顶点,控制数γ=1的树T,代数连通度α(T)=1.

证明若γ=1,此时只有一个图,就是星图K1,n-1.因为星图的拉普拉斯特征多项式为Φ(L(K1,n-1))=μ(μ-n)(μ-1)n-2,所以α(T)=μn-1(K1,n-1)=1.

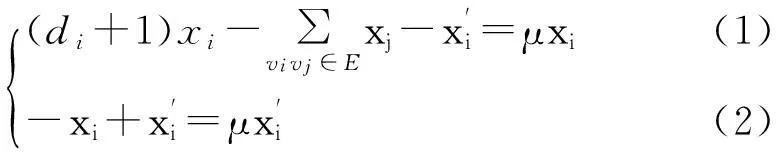
2.2控制数为γ=2的树.

对于任意的n阶树,要使它满足控制数γ=2,可以构造出下面三类树:(I)取一条具有4个顶点的路,在它的第2和第3个顶点处分别粘贴s1和t1条悬挂边,得到的图记为T1(s1,t1),γ=2s1+t1+4=n;(Ⅱ)取一条具有5个顶点的路,在它的第2和第4个顶点处分别粘贴s2和t2条悬挂边,得到的图记为T2(s2,t2),s2+t2+5=n;(Ⅲ)取一条具有6个顶点的路,在它的第2和第5个顶点处分别粘贴s3和t3条悬挂边,得到的图记为T3(s3,t3),s3+t3+6=n.如图1所示.

图1　控制数γ=2的三类树

定理4所有具有n个顶点,控制数γ=2的树中,树T=T3(s3,t3)具有最小的代数连通度.

证明因为dT2(v1)≥2,dT2(vw)=2,v1w是树T2(s2,t2)的割边,所以对T2(s2,t2)分离边v1w得到T1(s2+1,t2),由引理4可知,α(T2(s2,t2))α(T1(s2+1,t2)).而T1(s2+1,t2)≅T1(s1,t1),因此α(T2(s2,t2))α(T1(s1,t1)).

因为dT3(v1)≥2,dT3(vu)=2,v1u是树T3(s3,t3)的割边,所以对T3(s3,t3)分离边v1u得到T2(s3+1,t3),由引理4可知,α(T3(s3,t3))α(T2(s3+1,t3)).而T2(s3+1,t3)≅T2(s2,t2),因此α(T3(s3,t3))α(T2(s2,t2)).

所以,α(T3(s3,t3))α(T2(s2,t2))α(T1(s1,t1)).

[参考文献]

[1]HONG Y,ZHANG X D.Sharp upper and lower bounds for largest eigenvalue of the Laplacian matrix of trees[J].Discrete Math.,2005(296):187-197.

[2]GUO J M.On the Laplacian spectral radius of trees with fixed diameter[J].Linear Algebra Appl.,2006(419)：618-619.

[3]FENG L H,YU G H,LI Q.Minimizing the Laplacian eigenvalues for trees with given domination number[J].Linear Algebra Appl.,2006(419)：648-655.

[4]GUO J M.On the Laplacian spectral radius of a tree[J].Linear Algebra Appl.,2003(368)：379-387.

[5]FINK J F,JACOBSON M S,KINCH L F,et al. On graphs having domination number half their order[J].Period.Math.Hungar,1985(16):287-293.

[6]KIRKLAND S.A bound on the algebraic connectivity of a graph in terms of the number of cutpoints[J].Linear and Multilinear Algebra,2000(47)：93-103.

[7]FIEDLER M,PRAHA.Algebraic connectivity of graph[J].Czechoslovak Math.,1973(23):298-305.

[8]GUO J M.On the second largest Laplacian eigenvalue of trees[J].Linear Algebra Appl,2005(404):251-261.

[9]GUTMAN I.The star is the tree with greatest greatest Laplacian eigenvalue[J].Kragujevac J Math.,2002(24):61.

[责任编辑王新奇]

AlgebraicConnectivityofTreeswithGivenDominationNumber

GUAN Ting-ting

( School of Music, Anqing Normal University, Anqing 246133, China )

Abstract：The domination number γ(G) of a graph G(V,E) is the minimum cardinality of a subset of V, and it makes every vertex is either in the set S or adjacent to some vertices in the set S. In this paper, the algebraic connectivity of the tree T*=K1，∘K1with given domination number 1, was discussed, and the conclusion of the tree has the largest algebraic connectivity was got. At the same time, the polar graph with the smallest algebraic connectivity among trees in a given domination number 2 was depicted by using of shift in deformation, and the conclusion of the tree T=T3(s3,t3) has the smallest algebraic connectivity was got.

Key words：domination number; trees; algebraic connectivity

中图分类号：O157.5

文献标志码：A

作者简介：管婷婷(1984—)，女，安徽安庆人，安庆师范学院音乐学院助教，硕士，主要从事图论与网络优化研究.

收稿日期：2015-10-25

文章编号：1008-5564(2016)01-0005-03