捷联惯导系统的一种系统级标定方法

董春梅，陈希军，任顺清

(哈尔滨工业大学 空间控制与惯性技术中心，哈尔滨 150080)

捷联惯导系统的一种系统级标定方法

董春梅，陈希军，任顺清

(哈尔滨工业大学 空间控制与惯性技术中心，哈尔滨 150080)

针对三轴转台定位精度高的特点，设计了一种基于速度误差和姿态误差角作为观测量的系统级标定方法。在捷联惯性测量组合(SIMU)的导航误差方程和惯性器件误差参数模型的基础上，推导了导航速度误差和姿态误差角与IMU的误差参数所呈现的关系，依此给出了最简单的位置编排准则。通过观测不同位置下捷联惯导系统的速度误差变化率和姿态误差角,辨识IMU的误差模型系数，进而达到高精度捷联惯导系统标定目的。

捷联惯导；误差模型；系统级标定；翻滚试验

0 引言

IMU标定是一个确定IMU误差模型系数的过程，通过改变惯性仪表的原始输出到感兴趣的量，标定方法一般分为分立式标定和系统级标定[1-6]。

系统级标定滤波法的研究较多[7-11]，根据不同的应用场合，学者们设计了不同的滤波方案，但采用卡尔曼滤波算法，计算量大，可观测性分析复杂，标定时间长。文献[12]设计了一套转动激励编排方式，观测导航速度变化率拟合估计参数误差。文献[13]提出了一种利用低精度双轴转台对捷联惯导进行系统级标定的10位置标定方法，全面辨识出包括加速度计标度因数非线性项的24个系统误差系数。目前对于系统级标定文献的最大差异在于编排设计，但这些文献都没有给出标定位置编排的原因。

本文根据三轴转台可提供精确姿态的特点，将系统解算的姿态和转台的姿态作差，将姿态误差角作为观测量。提出了一种基于速度误差和姿态角误差作为观测量的系统级标定方法，从导航误差方程的原理出发，给出了最少且简便的位置编排准则，依据这个准则给定出具体的位置编排，大大缩短了标定时间并且该方法在低精度的转台上就可以实现。

1 惯导系统误差方程

本文选取I系为地心惯性坐标系，e系为地球坐标系，n系为导航坐标系(东北天坐标系)，b系为载体坐标系，a系为加速度计敏感轴系，g系为陀螺敏感轴系。捷联惯导系统由3只加速度计和3只陀螺组成。由于惯性仪表存在安装误差，为方便标定，一般定义载体系b系为[14-15]：xb轴与加速度计敏感轴单位矢量xa重合，yb轴在xaya平面内且与xb垂直，zb轴与xbyb一起构成右手直角坐标系。

根据定义，在载体系b中加速度计的误差模型为

(1)

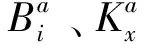
在载体系b中SIMU中陀螺的误差模型为

(2)

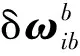
捷联惯性系统由3只陀螺和3只加速度计组成，因此捷联惯性导航的误差参数由加速度计和陀螺的误差参数如下21项组成：

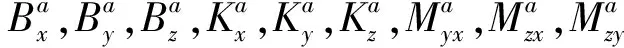
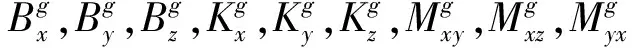
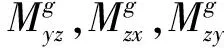
静基座条件下，忽略二阶小量后，捷联惯导系统导航误差方程可化简为[10]:

(3)

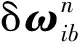
式(3)建立了IMU各误差参数和导航误差之间的关系，即速度误差δVn和姿态误差角Φ是关于IMU各误差参数的函数。如何通过捷联惯导系统不同的运动，利用速度误差δVn和姿态误差角Φ作为观测量，来辨识IMU的21项误差参数，是下面重点介绍的内容。

通过对系统翻滚前后的速度增量与姿态角误差变化，充分激励出IMU的各误差参数加以标定。捷联惯导系统在位置翻滚过程中，从t=t0的初始位置转动到t=T的最终位置引起的姿态误差角为

(4)

从t=t0的初始位置转动到t=T的最终位置，在x、y方向上的两个水平速度误差变化率的差分量表现为：

(5)

(6)

而从t=t0的初始位置转动到t=T的最终位置，在z方向的向上速度误差变化率的差与和分量表现为：

(7)

(8)

2 标定原理与标定编排设计

当系统处于不同的位置时，IMU的各误差参数对速度误差δVn和姿态误差角Φ的贡献不同。结合IMU误差参数模型式(1)、式(2)和式(4)～式(8)之间的关系可以估计式(1)、式(2)中的误差模型系数。

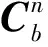
定理1(充分条件)若要充分激励出加速度计的各项误差参数，至少需要7个位置即可。位置编排需满足以下条件：

C13T+C13t0≠0 orC23T+C23t0≠0;

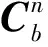
(9)

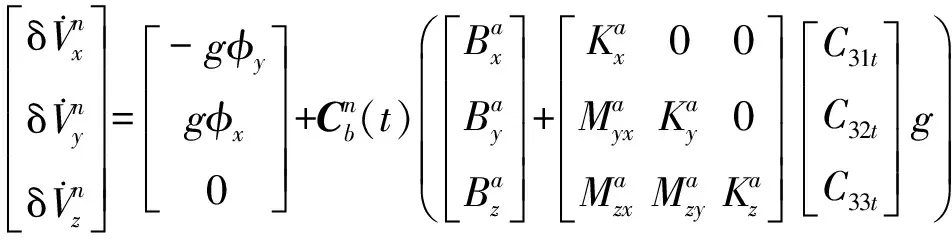
(10)

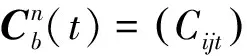
C31t=±1orC32t=±1orC33t=±1

(11)

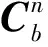
(12)

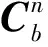
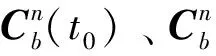
(13)

(14)

(15)

(16)

C3jt0=1,C3jT=-1or

C3jt0=-1,C3jT=1(j=1,2,3)

(17)

以x加速度计位于天地方向为例，若t0时刻位置x加速度计朝天，T时刻位置x加速度计朝地，即C31t0=1,C31T=-1。根据式(15)、式(16)可求得：

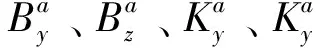
(18)

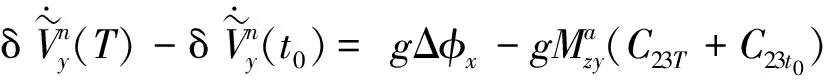
(19)

C13T+C13t0≠0 orC23T+C23t0≠0

证得条件2)。

(20)

(21)

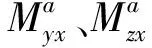
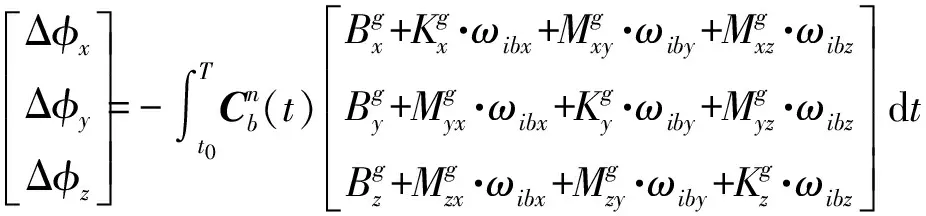
(22)

为了辨识式(22)中陀螺的各误差模型系数，实质上就是对式(22)积分后，求解其中的12个误差参数。若要对12个未知的误差参数进行求解，至少需要4次转动角速率才能通过式(22)得到12个观测方程。

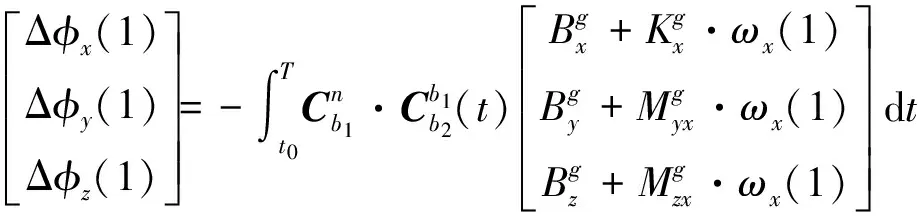
(23)

式中，Δφi(j)、ωi(j)分别为第i方向陀螺的j次转动的姿态误差角观测量与角速率(i=x、y、z，j=1、2、3、4)。

同理，第2、3次转动分别为y、z方向的陀螺，依据式，忽略二阶小量后可得：

(24)

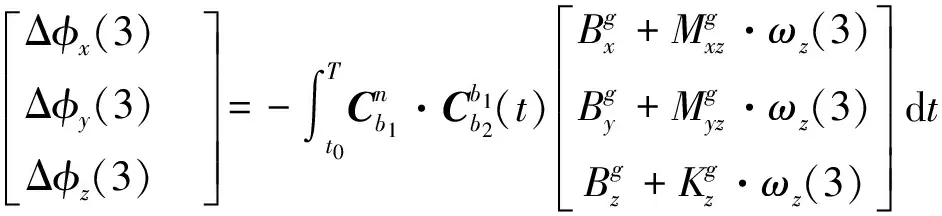
(25)

假设在第4次转动中选取x方向的陀螺，同理依据式，忽略二阶小量后也有

(26)

将式(23)～式(26)积分后，可分别化成下列方程：

(27)

式中，ap(j)是通过对式(23)～式(26)积分后，姿态误差角Δφi(j)的代数组合(p=1、2、3，j=1、2、3、4)。

式(27)将陀螺误差模型中辨识12项误差参数的问题，转化为方程组的求解问题。下面以式中4个方程组的第一个方程为例进行分析：

(28)

(29)

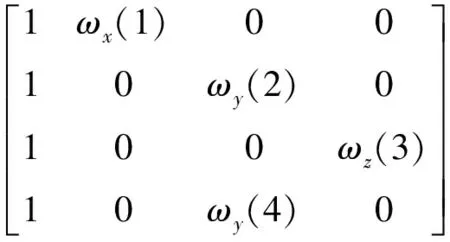
上述定理1和定理2给出了辨识IMU各误差系数的充分条件，以此为参考准则来设计位置编排。

记第i组旋转前t0=0时刻的位置为j-1，旋转后T时刻的位置为j-2(j=1、2、3、4)。表1所示为一组可行的位置编排。

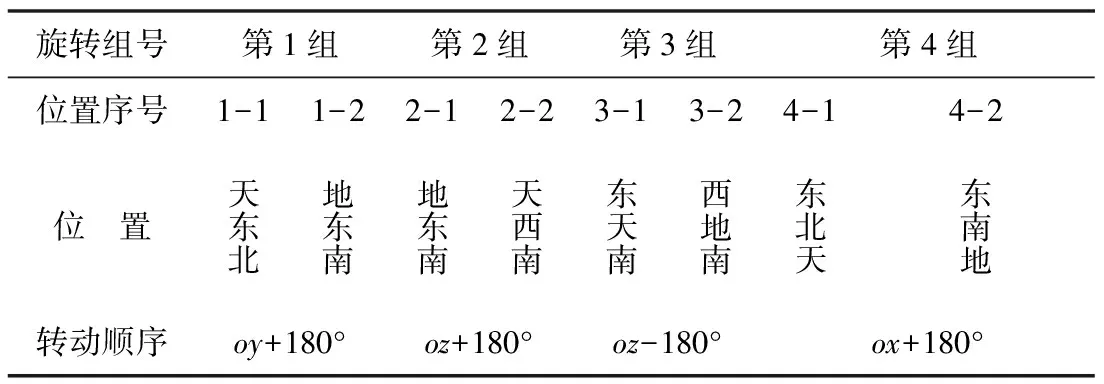
表1 位置编排旋转

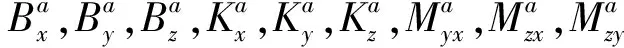
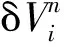
1)标定零偏和刻度因子误差。依据x、y、z加速度计分别朝天、朝地方向的位置(表1中的7个位置)和式(15)、式(16)可得：

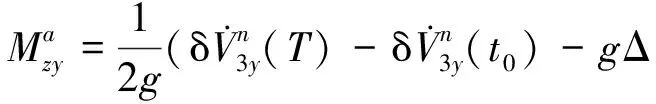
其次，惯导系统在进行标定编排旋转之后，将姿态角误差作为观测量可对陀螺的误差参数进行标定。

设第j组编排旋转得到的姿态误差角观测量为ΔΦj。下面以第1组标定编排旋转为例，根据姿态误差式(4)有

(30)

(31)

(32)

式中，ap(j)为第p个方程的j次转动得到的观测值(p=1、2、3，j=1、2、3、4)。

同理，在第2组标定编排旋转下，依据导航姿态误差方程有：

(33)

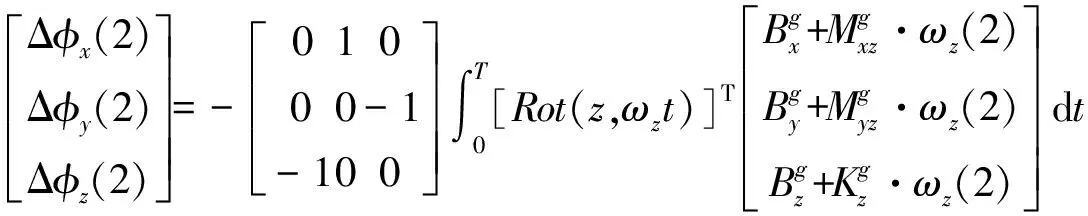
(34)

对式(34)计算后，可得：

(35)

第3组标定编排旋转下，依据导航姿态误差方程有：

(36)

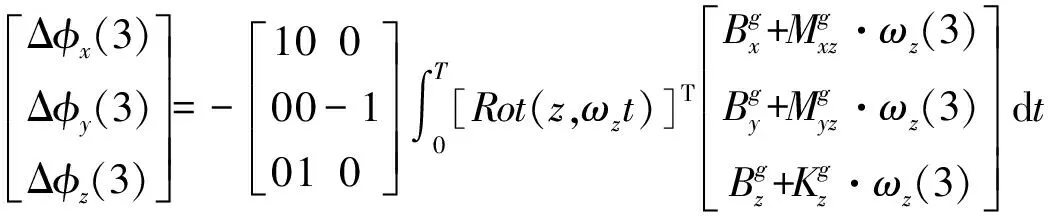
(37)

(38)

在第4组标定编排旋转下有：

(39)

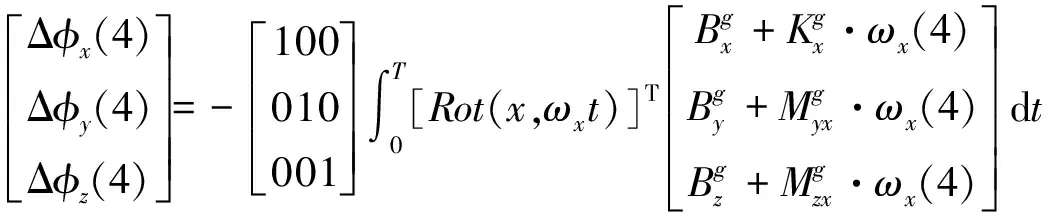
(40)

对式(40)计算后，可得：

(41)

将式(32)、式(35)、式(38)、式(41)中的各方程写成式(27)的形式后，又由于表1位置编排中第2组和第3组的标定转动角速率ωz(2)=-ωz(3)，满足定理2的条件，于是容易求解出陀螺的12项误差参数。求解过程简单，限于篇幅此处不再赘述。

3 仿真验证

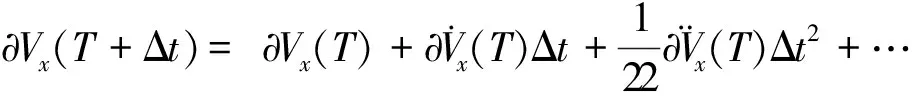
(42)

当时间间隔Δt为小量时，忽略二阶小量后，由式(42)可得

(43)

仿真条件设置为：假设当地纬度为北纬45°，加速度计和陀螺测量噪声为10-5g(1σ)和0.01(°)/h(1σ)，第1、2、4组的转速设为10(°)/s，第3组的转速设为20(°)/s，不考虑其他误差；捷联惯导系统中3只加速度计和3只陀螺的仿真标定结果如表2所示。

表2 陀螺和加速度计的误差参数估计结果

从表2可以看出，陀螺和加速度计的各误差参数都有很好的估计，陀螺和加速度计的零偏标定误差均小于0.005(°)/h和0.005mg，安装误差角的标定误差均小于2，标度因子误差的标定误差小于10-6。同时，对编排的仿真结果验证了本文设计的系统级标定方法的正确性，在所提出的方案设计中，编排的位置都为正交位置，系统的标定精度不受转台精度的限制，便于现场标定，进一步为高精度捷联惯组系统的标定设计提供了理论依据。

4 结论

本文研究了一种基于速度误差和姿态角误差的系统级标定方法，建立了IMU各误差参数和导航误差方程的关系。通过捷联惯组系统翻滚前后姿态角误差的变化量与速度增量，充分激励出IMU的各误差参数加以标定。从导航误差方程的原理出发，设计出最简的位置编排准则，缩短了更多的标定时间。通过理论分析和仿真研究表明，给出的标定原理与标定编排的设计正确，能准确估计出IMU各误差参数。位置编排简单，标定时间短，具有较强的工程应用价值。

[1] 党建军, 罗建军, 万彦辉. 基于单轴速率转台的捷联惯测组合标定方法[J].航空学报，2010，31 (4):806-811.

[2] Yang J, Tao H. Research of micro-mechanical gyro measurement methods[C]// Proceedings of the International Symposium on Test and Measurement, 2009: 45-48．

[3] Xu B, Hao Y L. Error analysis of the attitude updating algorithm for submarine in the dynamic environment [C] //Proceedings of the IEEE International Conference on Mechatronics and Automation, 2011: 2183-2188.

[4] Yuan B, Liao D, Han S. Error compensation of an optical gyro INS by multi-axis rotation [J].Measurement Science and Technology, 2012, 23 (2):1-9.

[5] Zheng Z, Gao Y , He K . Systematic calibration method for FOG inertial measurement units [J]. Advanced Materials Research, 2013(662): 717-720.

[6] Babichenko A V, Shkred V K. Main errors of inertial navigation systems [J]. Engineering Physics, 2011, 11(3): 34-53.

[7] 杨晓霞, 孟浩然,王帅.激光捷联惯导系统的外场动态标定方法[J].中国惯性技术学报, 2011, 19(4): 393-398.

[8] Grewal M S, Henderson V D, Miyasako R S. Application of Kalman filtering to the calibration and alignment of inertial navigation systems [J].Automatic Control, IEEE Transactions on, 1991, 36(1): 3-13.

[9] 胡倩倩,曾庆化,宋国安, 陈维娜.一种数据融合车载捷联惯导系统在线标定方法[J].计算机仿真, 2012, 29(8): 336-339.

[10] 盛宏媛.光纤陀螺捷联惯导系统级标定方法的研究[D].哈尔滨工程大学,2012.

[11] 蔚国强,杨建业,张合新.改进的TSKF算法及其在惯组系统级标定中的应用[J].电光与控制,2011, 18(6): 45-49,97.

[12] Lee T G , Sung C K . Estimation technique of fixed sensor errors for SDINS calibration[J] . International Journal of Control, Automation, and Systems , 2004 , 2(4): 536-541.

[13] 周章华, 邱宏波, 李延. 用低精度双轴转台对捷联惯导进行系统级标定的方法[J].中国惯性技术学报, 2010, 18(4): 503-507.

[14] Zhang H, Wu Y, Wu W. Improved multi-position calibration for Inertial measurement units [J] . Measurement Science and Technology, 2010, 21(1): 209-213.

[15] 谢波，秦永元，万彦辉. 激光陀螺捷联惯导系统多位置标定方法[J]. 中国惯性技术学报，2011，19(2)：157-162.

Systematic Calibration Method for Strapdown Inertial Navigation System

DONG Chun-mei, CHEN Xi-jun, REN Shun-qing

(Space Control and Inertial Technology Research Center, Harbin Institute of Technology, Harbin 150080, China)

Aiming at high precision positioning feature of the three-axis turntable，a new kind of systematic calibration method is presented based on observing velocity error and attitude angle error. Based on the navigation error equation of laser strapdown inertial navigation system and error model of inertial measurement unit, the relationship between velocity error and IMU error is deduced, and then the simplest location layout principles is given. By observing velocity error and attitude angle error of navigation system in every position, the IMU error model coefficients is identified, so the goal to calibrate high precision strapdown inertial navigation system is achieved.

Strapdown inertial navigation system;Error model;Systematic calibration;Tumble test

10.19306/j.cnki.2095-8110.2016.04.014

2014-07-08；

2014-09-11。

十二五预研项目(51309050202)

董春梅(1986-)，女，博士，从事惯性组合测试方法研究。E-mail：dcmjob@126.com

U666.1

A

2095-8110(2016)04-0074-07