标准轨迹制导中准平衡滑翔条件优化研究

熊子豪，任 章，江若冲，陈 建

(1.北京航空航天大学 自动化科学与电气工程学院, 北京 100191； 2.北京航空航天大学 飞行器控制一体化技术国防科技重点实验室, 北京 100191； 3.中国人民解放军军械工程学院 弹药工程系, 石家庄 050001)

标准轨迹制导中准平衡滑翔条件优化研究

熊子豪1,2，任 章1,2，江若冲3，陈 建1,2

(1.北京航空航天大学 自动化科学与电气工程学院, 北京 100191； 2.北京航空航天大学 飞行器控制一体化技术国防科技重点实验室, 北京 100191； 3.中国人民解放军军械工程学院 弹药工程系, 石家庄 050001)

对于可重复使用运载器标准轨迹再入制导，准平衡滑翔条件可以将高度-速度平面内各项再入约束形成的飞行走廊，转换为倾侧角-速度空间内的倾侧角走廊。通过在倾侧角走廊内设计倾侧角曲线，可以生成满足飞行走廊的标准轨迹。通过论证标准轨迹再入制导过程中的准平衡滑翔条件及其物理意义，说明了由倾侧角走廊内的倾侧角曲线生成的标准轨迹，存在突破再入飞行走廊边界的可能性。通过对倾侧角走廊边界设置余度，极大地降低了标准轨迹突破再入飞行走廊边界的可能性，提高了标准轨迹的设计成功率。

可重复使用运载器；再入制导；轨迹规划；准平衡滑翔条件；再入走廊

0 引言

再入段是可重复使用运载器从太空返回地面的重要飞行阶段[1]。再入制导方法的科学设计除了保证飞行器平稳顺利的再入过程，还可以使飞行器满足各项飞行约束[2]，因此再入制导方法成为可重复使用运载器研制中的一项核心关键技术。目前，再入制导方法可以分为标准轨迹再入制导方法和预测再入制导方法两种[3]。相比于预测再入制导方法对机载硬件和算法可靠性具有较高要求[4-6]，标准轨迹再入制导方法计算量少、可靠性和制导精度高[7]，已经成功应用于Apollo再入制导[8]、航天飞机再入制导[9]以及其他飞行器的再入过程，具有实际工程应用价值。

设计一条满足再入飞行各项约束，并可以完成所需航程等飞行任务的再入标准轨迹，是保证标准轨迹再入制导成功实行的基础。通过引入再入飞行走廊的概念[10]，可以在纵向运动参数构成的坐标面内绘制再入各项约束，形成再入飞行走廊的边界，为标准轨迹的设计提供直观的允许范围。目前比较常用的再入飞行走廊平面除了航天飞机应用的阻力加速度-速度平面[9]，还有阻力加速度-能量平面[11]和高度-速度平面[12]。X-33验证机[13-14]的再入标准轨迹规划中将航程、热流和动压等限制转换到阻力加速度-能量平面，然后用最优仿真程序进行标准轨迹优化设计。此外，一些新的理论方法如直接配点法[15]、遗传算法[16]、伪谱法[17]等也逐渐应用到标准轨迹的设计和优化中。

为了应对再入飞行中存在复杂多变的各种情况，国内外的研究人员研究发展了标准轨迹快速设计方法。文献[12]引入了准平衡滑翔条件(Quasi- Equilibrium Glide Condition, QEGC)的概念，快速设计满足航程等飞行任务的倾侧角曲线，并生成相应的满足再入飞行走廊边界的标准轨迹。然而由于可重复使用运载器并不严格满足平衡滑翔条件，虽然设计的倾侧角曲线满足倾侧角走廊边界，但生成的标准轨迹存在突破再入飞行走廊边界的情况。本文通过对可重复使用运载器再入飞行过程中准平衡滑翔条件的验证，说明了标准轨迹可能突破飞行走廊边界的原因。通过对倾侧角走廊设置一定的余度，在新的倾侧角走廊内设计标准倾侧角曲线，优化了标准轨迹的设计方法，极大地降低了标准轨迹突破再入飞行走廊边界的可能性。

1 基于高度-速度平面的再入制导标准轨迹规划

1.1 再入飞行基于高度-速度平面的飞行走廊

再入制导标准轨迹是指可重复使用运载器再入飞行过程中，在某一参数平面内满足各类飞行约束的再入飞行参数曲线。再入过程中，复杂的飞行环境及飞行器硬件条件的限制，对再入飞行构成了一定的约束。根据再入飞行受到的不同影响，可分解出如下主要约束：

(1)

法向过载nN满足式(2)

nN=Lcosα+Dsinα≤nN.max

(2)

其中，L是升力，D是阻力，α是攻角，nN.max是法向过载极限值。

动压q需低于极限值qmax，满足式(3)

(3)

大气密度采用指数形式，如式(4)所示

(4)

其中，ρ0=1.225kg/m3、Hs=6700m。

(5)

在高度-速度平面内，由式(5)确定的热流、法向过载、动压约束边界如图1所示。

图1 再入飞行热流、法向过载、动压约束边界Fig.1 Reentry flight constraints of heating flow, normal overload and dynamic pressure

图1所示为高度-速度平面内的热流、法向过载、动压约束边界，其中实线是最大驻点热流高度边界，圆点线是最大法向过载高度边界，虚线是最大动压高度边界。在每一速度状态下，三条高度边界的最大值，确定为当前速度下的飞行走廊下边界Hmin(V)，如图 2中的实线所示。

图2 高度-速度平面内再入飞行走廊的下边界Fig.2 Reentry corridor low boundary in high-velocity plane

用θ表示航迹角，L表示升力，σ表示倾侧角，g表示重力加速度，r表示飞行器位置矢径，飞行器航迹角微分方程如下

(6)

(7)

其中，重力加速度g=fg(H)，确定攻角-速度曲线后，式(7)仅与高度、速度、倾侧角有关。因此，式(7)是飞行器满足平衡滑翔条件的情况下，关于高度、速度、倾侧角3个变量的关系式，由其中任意2个参数可以计算得到第3个参数值。如图3所示。

图3 基于平衡滑翔条件的参数关系图Fig.3 Parameter-relation chart based on EGC

图4 高度-速度平面再入飞行走廊Fig.4 Reentry corridor in high-velocity plane

1.2 标准轨迹规划

在标准轨迹的设计中，希望通过设计标准的制导指令，生成一条满足飞行走廊边界的标准轨迹，并满足航程等飞行任务。以倾侧角σ(V)为制导信号，设计标准倾侧角指令，并生成满足飞行走廊边界的标准轨迹流程如图5所示。

图5 设计标准倾侧角指令并生成标准轨迹流程Fig.5 Flow chart of bank angle signal design and reference trajectory planning

2 准平衡滑翔条件及论证

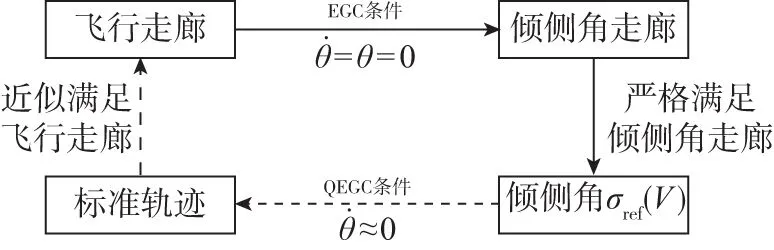
图6 设计标准倾侧角指令并生成满足QEGC标准轨迹流程图Fig.6 Flow chart of bank angle signal design and reference trajectory planning satisfying QEGC

图7 倾侧角走廊及标准倾侧角指令Fig.7 Bank angle corridor and bank angle signal

图8 飞行走廊及标准轨迹Fig.8 Reentry corridor and reference trajectory

图9 标准轨迹与航迹角导数的对比图Fig.9 Reference trajectory and derivative of path angle

3 标准轨迹规划的优化

3.1 标准轨迹规划存在的问题

在倾侧角走廊内设计的标准倾侧角指令若接近走廊的边界，则标准倾侧角指令通过式(7)计算得到的平衡滑翔曲线会接近飞行走廊的边界。通过标准倾侧角指令、飞行器运动学方程、动力学方程生成的标准轨迹并不严格满足平衡滑翔条件，因此标准轨迹会围绕平衡滑翔曲线上下波动。由于平衡滑翔曲线接近飞行走廊的边界，因此围绕平衡滑翔曲线上下波动的标准轨迹可能存在超出飞行走廊边界的情况，如图10和图11所示。

图10是倾侧角走廊内标准倾侧角指令的设计曲线，虚线是倾侧角走廊的上边界，实线是设计完成的标准倾侧角指令。从图10中可以看出，在速度约2700～3700m/s的范围内，倾侧角指令十分接近倾侧角走廊的上边界。图11是由图10中设计的标准倾侧角指令结合飞行器运动学方程、动力学方程生成的标准轨迹，实线是标准轨迹，虚线飞行走廊的下边界，电话线是飞行走廊的上边界。从图11中可以看出，在速度约2700～3700m/s的范围内，标准轨迹突破了飞行走廊的下边界，设计产生的标准轨迹无法满足再入飞行的约束。

图10 标准倾侧角指令的设计曲线Fig.10 Bank angle signal inside bank angle corridor

图11 超出再入走廊的标准轨迹Fig.11 Reference trajectory exceeds reentry corridor

3.2 标准轨迹规划的优化

为了使设计得到的标准轨迹无法突破飞行走廊的边界，本文对标准倾侧角指令的设计方法进行改进，以此对标准轨迹的设计方法进行优化。将倾侧角-速度平面内倾侧角走廊的边界缩小一定比例，使缩小后新的倾侧角走廊边界与初始倾侧角走廊边界之间产生一定的余度。在新的倾侧角走廊内设计的标准倾侧角指令σnew(V)，与初始倾侧角走廊边界之间会存在同样的余度。由σnew(V)通过式(7)计算得到的平衡滑翔曲线在高度-速度平面内与再入走廊的边界也会保持同样的余度。因此，围绕平衡滑翔曲线上下波动的标准轨迹，很难突破飞行走廊的边界，极大地减小了标准轨迹无法满足再入飞行约束的可能性。

关于新的倾侧角走廊与初始倾侧角走廊之间余度值的设定，若余度值偏小，则对于标准轨迹规划的改进效果有限；若余度值偏大，则新的倾侧角走廊相对于初始倾侧角走廊会减小很多，在新的走廊内可能无法设计出满足所需航程等飞行任务的标准倾侧角指令。因此，余度值需要设定一个合适的数值，通常取5% 。改进后的设计方法和标准轨迹如下所述。

以图10中的倾侧角走廊为初始倾侧角走廊，设置5%余度后，新的倾侧角走廊及设计的标准倾侧角指令σnew(V)曲线如图12所示。其中，圆点线是初始倾侧角走廊边界，虚线是设置5%余度的新倾侧角走廊边界，实线是设计的标准倾侧角指令σnew(V)。从图12中可以看出，标准倾侧角指令与初始倾侧角走廊边界存在至少5%的余度空间。

图12 设定5%余度值的倾侧角走廊及标准倾侧角指令Fig.12 Bank angle signal inside bank angle corridor with 5% margin

图13是在高度-速度平面内，由图 12中设计的标准倾侧角指令σnew(V)生成的飞行器再入飞行标准轨迹。其中，实线是标准轨迹，点划线和虚线分别是飞行走廊的上边界和下边界。从图13中可以看出，由5%余度倾侧角走廊内新的倾侧角指令生成的标准轨迹，没有超出飞行走廊的边界，满足再入飞行的各项约束。

图13 优化后的标准轨迹Fig.13 Reference trajectory inside reentry corridor

4 结论

仿真验证表明，可重复使用运载器再入飞行的标准轨迹近似满足平衡滑翔条件，即满足准平衡滑翔条件。而基于平衡滑翔条件在倾侧角走廊设计标准倾侧角指令并生成相应标准轨迹的方法，由于飞行器并不严格满足平衡滑翔条件，所以存在标准轨迹突破飞行走廊无法满足约束的情况。通过设置余度，得到新的倾侧角走廊，并在新的走廊内设计标准倾侧角指令，可以确保生成的标准轨迹不突破飞行走廊的边界，满足再入飞行的相关约束，从而极大地提高标准轨迹的设计成功率。

[1] 赵汉元.航天器再入制导方法综述[J].航天控制,1994(1):26-33.

[2] 汪朝群.航天飞机的再入飞行走廊及再入飞行轨迹[J].航天控制,1990(1):1-10.

[3]WingroveRC.Surveyofatmospherere-entryguidanceandcontrolmethods[J].AiaaJournal,1963,1(9):2019-2029.

[4]MeaseK,ChenD,TandonS,etal.Athree-dimensionalpredictiveentryguidanceapproach[C].AIAAGuidance,NavigationandControlConferenceandExhibit.AmericanInstituteofAeronauticsandAstronautics,2000.

[5]HusseinY,RajivC,HowardL,etal.Predictor-correctorentryguidanceforreusablelaunchvehicles[C].AIAAGuidance,NavigationandControlConferenceandExhibit.AmericanInstituteofAeronauticsandAstronautics,2001.

[6] 潘乐飞,李新国.可重复使用运载器预测-校正再入制导研究[J].飞行力学,2007,25(1):55-58.

[7] 胡建学,陈克俊,赵汉元,等.RLV再入标准轨道制导与轨道预测制导方法比较分析[J].国防科技大学学报,2007,29(1):26-29.

[8]GravesCA,HarpoldJC.Apolloexperiencereport:missionplanningforApolloentry,NASA-TN-D-6725[R].Washington:NASA, 1972.

[9]HarpoldJC,GravesCA.Shuttleentryguidance[J].JournaloftheAstronauticalSciences,1979,27(3):239-268.

[10] 南英,吕学富,陈士橹.航天器的再入走廊及其计算方法[J].飞行力学,1993,11(2):34-43.

[11]RoennekeAJ,MarklA.Re-entrycontroltoadrag-vs-energyprofile[J].JournalofGuidanceControlandDynamics,1994, 17(5):837-844.

[12]LuP,ShenZJ.On-boardgenerationofthree-dimensionalconstrainedentrytrajectories[J].JournalofGuidanceControlandDynamics,2003, 26(1):111-121.

[13]LuP,JohnMH.EntrytrajectorydesignfortheX-33vehicle[C].22ndAtmosphericFlightMechanicsConference.AmericanInstituteofAeronauticsandAstronautics,1997.

[14]HillAD,AndersonDM,CoughlinDJ,etal.X-33trajectoryoptimizationanddesign[J].AiaaJournal,1998.

[15] 涂良辉,袁建平,岳晓奎,等.基于直接配点法的再入轨迹优化设计[J].西北工业大学学报,2006,24(5):653-657.

[16] 陈刚,胡莹,万自明,等.基于遗传算法的RLV再入轨迹优化设计[J].固体火箭技术,2006,29(4):235-238.

[17] 雍恩米,唐国金,陈磊.基于Gauss伪谱方法的高超声速飞行器再入轨迹快速优化[J].宇航学报, 2008, 29(6):1766-1772.

Demonstration and Improvement of Quasi-equilibrium Glide Condition in Reference Trajectory Reentry Guidance

XIONG Zi-hao1,2, REN Zhang1,2, JIANG Ruo-chong3, CHEN Jian1,2

(1.School of Automation Science and Engineering, Beijing University of Aeronautics and Astronautics, Beijing 100191, China； 2.Science and Technology on Aircraft Control Laboratory, Beijing University of Aeronautics and Astronautics, Beijing 100191, China; 3.Department of Ammunition Engineering, Ordnance Engineering College, Shijiazhuang 050001, China)

For reference trajectory reentry guidance process for reusable launch vehicle, the reentry corridor calculated by various constraints based on altitude-velocity plane can be translated to bank angle corridor based on bank angle velocity plane through quasi-equilibrium glide condition(QEGC).Bank angle signal designed in bank angle corridor can generate a reference trajectory inside reentry corridor generally.This paper gives an argument of QEGC and its physical meaning in reference trajectory reentry guidance, and demonstrates the possibility that reference trajectory generated by bank angle signal inside bank angle corridor can exceed the reentry corridor.A method of setting bank angle corridor margin is proposed to reduce the likelihood of generating a reference trajectory which exceeds the reentry corridor boundary.This approach improves reference trajectory generating method effectively.

Reusable launch vehicle; Reentry guidance; Trajectory planning; Quasi equilibrium glide condition; Reentry corridor

10.19306/j.cnki.2095-8110.2016.04.009

2015-09-25；

2015-10-26。

国家自然科学基金(91316304, 61333011, 61121003, 61101004)

熊子豪(1987-)，男，博士，主要研究方向为飞行器制导与控制。E-mail：xzih007@126.com

V448.2

A

2095-8110(2016)04-0047-06