基于层次评估理论的弹道导弹末段突防制导律研究

葛云鹏，杨 军，袁 博，朱学平

(西北工业大学 航天学院，西安 710072)

基于层次评估理论的弹道导弹末段突防制导律研究

葛云鹏，杨 军，袁 博，朱学平

(西北工业大学 航天学院，西安 710072)

针对弹道导弹末段突防问题，应用层次性能评估体系，对弹道导弹末段典型突防制导律进行对比分析。并通过对弹道导弹制导精度、弹道导弹最大过载、弹道飞行时间和反导导弹脱靶量以及它们的均值、均方差的重要性和需求性分析，合理设置评估体系的指标及其权值，应用随机仿真分析方法，对比仿真经典比例导引、修正比例导引和变结构比例导引三种突防制导律的性能。仿真结果证明，层次评估理论可以用于弹道导弹末段突防制导律的评估及优选。

弹道导弹；制导律；层次性能评估体系

0 引言

在未来的高技术战争中，弹道导弹作为一种远程有效的精确打击手段将越来越广泛地应用于战争中。因为战争中弹道导弹不仅仅只是一件武器，更重要的是它具备极强的战略威慑作用，已经成为决定战争胜负的重要因素。因此，弹道导弹的生存问题,即弹道导弹突防问题已经成为当下弹道导弹制导律和制导策略研究的重点问题。

弹道导弹飞行大致可以分为三个基本阶段，即上升阶段，外大气层阶段和再入段。而为了保证弹道导弹的生存，顺利突破导弹防御系统的拦截，故而在弹道导弹的各个阶段进行相应的机动，以此保证其生存性。然而，由于上升阶段一般位于本国境内，故而一般只针对弹道导弹的中制导段和末制导阶段进行相应的机动突防研究。

本文在考虑导引头测量噪声的基础上，应用层次评估理论和随机仿真分析方法，综合考虑弹道导弹制导精度、弹道导弹最大过载、飞行时间和反导脱靶量四项性能指标，提出针对弹道导弹末段突防的指标系数，建立层次评估体系。以此对经典比例导引(不同制导系数)、修正比例导引和变结构比例导引进行对比仿真分析,仿真结果证明层次评估理论对弹道导弹末制导突防制导律的选择具有可行性。

1 仿真数学模型

针对弹道导弹突防制导律的研究问题，分别建立相应的弹道导弹数学模型、反导导弹数学模型和层次评估体系。

1.1 弹道导弹数学模型

在研究导弹运动型模型之前，我们首先提几点假设：

1)忽略地球自转影响；

2)仅考虑导弹的质心运动，忽略绕质心的转动。

由此可以得到在弹道坐标系下的三自由度质心运动学模型，如式(1)所示:

(1)

1.2 反导系统数学模型

反导导弹也采用三自由度质心运动学模型，形式与式(1)的弹道导弹数学模型类似，只是速度特性不同。反导导弹以来袭的弹道导弹为攻击目标，其特点是：

1)反导导弹的飞行速度小于来袭导弹的飞行速度；

2)目标和导弹以很高的速度接近，为了能够精确地导引导弹沿着理想弹道接近目标，往往需要有较大的法向过载来实现控制。

但是拦截弹所能提供的法向过载有限，往往由于过载饱和而引起很大的脱靶量。同时，对于拦截弹道导弹的拦截弹来说，弹道导弹相对于一般空中目标的速度太大，传统的尾追式拦截已经无法命中目标。而如果采用迎面拦截方式，将造成弹目之间相对速度过大。同时由于经典比例导引不满足速度比要求，拦截弹末段视线角速率发散，拦截弹无法有效拦截目标。因此，为了对弹道导弹末段进行有效拦截，我们选用一种新型的带拦截点预测的比例导引律。

拦截点预测方法如下：

(2)

(3)

式中，τ为随时间变化的量，在遭遇点应保证τ=0；Rm、Rc，qm分别为弹道导弹，拦截弹相对于以弹道导弹目标点为圆心的地面坐标的位置。其中，Rm、Rc代表弹道导弹和目标相对于坐标原点的距离，qm代表弹道导弹相对于坐标原点的视线角。

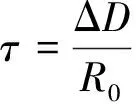
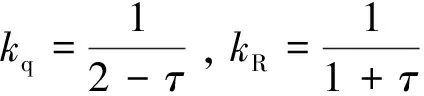
1.3 层次分析体系

应用AHP(AnalyticHierarchyProcess,层次分析理论)，首先要把弹道导弹突防问题条理化、层次化，构造出弹道导弹突防的结构模型。为此先要分析影响弹道导弹突防性能的各个因素，并对其进行重要性分析，构造出层次模型的判断矩阵，继而计算相应的突防性能分数。

弹道导弹末段突防就是要在保证弹道导弹高生存能力的前提下，使其具有高命中精度。因此，针对命中精度，本文提出制导精度指标作为评估指标。同时对于生存性问题，由于弹道导弹末段突防中要对抗各种反导系统和导弹，因此高机动性能能够保证弹道导弹规避反导导弹的拦截，小飞行时间可以减小反导系统反应时间，保证弹道导弹的成功突防。所以，为了评估弹道导弹的生存性，本文提出了反导脱靶量、弹道导弹最大过载和弹道导弹飞行时间三项性能指标。综合前述的制导精度指标，本文建立如图1所示的性能评估体系。

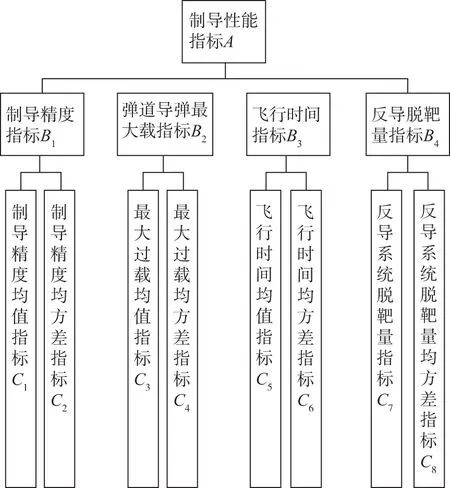
图1 制导性能评估体系框图Fig.1 The diagram of guidance assessment

图1中的制导性能A估算步骤如下：

1)C1～C8指标的计算

首先选定仿真条件，以弹道导弹应用制导系数为4的经典比例导引为基准状态(目标无干扰)，通过蒙特卡洛仿真得到基准状态对应的脱靶量、最大过载、飞行时间和反导脱靶量的均值及方差；然后对应用不同突防制导律的弹道导弹进行蒙特卡洛仿真，可得到对应的脱靶量、飞行时间、最大过载和反导脱靶量的均值及均方差，则C1～C8指标计算如下：

式中：

Ed0—基准状态弹道导弹的脱靶量均值；

Ed—待评估状态弹道导弹的脱靶量均值；

σd0—基准状态的弹道导弹脱靶量均方差；

σd—待评估状态的弹道导弹脱靶量均方差；

En0—基准状态弹道导弹最大过载均值；

En—待评估状态弹道导弹最大过载均值；

σn0—基准状态弹道导弹最大过载均方差；

σn—待评估状态弹道导弹最大过载均方差；

Et0—基准状态弹道导弹飞行时间均值；

Et—待评估状态弹道导弹飞行时间均值；

σt0—基准状态的弹道导弹飞行时间均方差；

σt—待评估状态的弹道导弹飞行时间均方差；

Em0—基准状态反导导弹脱靶量；

Em—待评估状态反导导弹脱靶量；

σm0—基准状态反导导弹脱靶量均方差；

σm—待评估状态反导导弹脱靶量均方差。

由于反导导弹杀伤半径一般在20～30m，仿真测试预留10m的脱靶量余量。故而认为反导导弹脱靶量大于40m时反导脱靶，弹道导弹成功突防；而小于40m时认为弹道导弹有被拦截的可能性。对评估体系做如下修正：

2)B1～B4指标的计算

B1～B4指标的计算方法如下：

式中λC1～λC8为第三层指标的加权因子。

3)制导性能指标A的计算

A=λB1B1+λB2B2+λB3B3+λB4B4

式中λB1～λB4为第二层指标的加权因子。

上面的加权因子可借鉴AHP的1～9判断尺度来确定。具体数值如表1所示。

表1 AHP判断尺度

本文中针对弹道导弹末段突防问题，首先对B1～B4的指标加权因子进行分析判断。在弹道导弹末段突防中，由于弹道导弹成功突防是保证毁伤的前提条件，故而反导脱靶量在评估体系中占绝对重要的地位。其次制导精度决定了弹道导弹的毁伤效果，故而这点在指标评估体系中占重要的地位。而飞行时间和最大过载指标，由于弹道导弹的最大过载影响导弹突防性能和反导脱靶量，因此其在性能指标体系中排第四的位置；又因为飞行时间对于弹道导弹末段突防来说相对属于最不重要的地位，因此排在最后一位。

对于B1～B4的指标进行定性分析后，针对B1～B4每一项的均值和均方差分别进行重要性和需求性分析，完成对C1～C8的权值设定。

具体矩阵形式如下所示：

通过层次排序及一致性检验计算一致性比例CR如下所示

其中,CI为计算一致性指标，RI为一致性指标。

已知一致性比例满足CR<0.10的要求时，认为判断矩阵A是可以接受的，故本文所述判断矩阵合理。同理B1～B4的检验方法与A矩阵检验方法类似，经验证B1～B4矩阵满足要求，可以应用于弹道导弹突防仿真测试。

2 仿真分析

仿真中引入导引头的测量噪声和惯导位置误差，以此应用层次分析法对制导律性能进行研究。针对弹道导弹突防问题仿真，作出以下仿真初始假设：

1)弹道导弹攻击目标为固定目标，目标初始位置为(50000m，0，0)，反导导弹初始位置与目标位置初始位置相同，反导导弹速度始终为1000m/s，初始弹道倾角为90°，弹道偏角都为0°；

2)弹道导弹初始位置为(0，20000m，0)，初始速度为1500m/s，初始弹道倾角和弹道偏角都为0°；

3)假定弹道导弹导引头的测角误差均值为0°,均方差为0.008°；

4)为了简化验证制导律的性能，仅对纵向平面进行弹道仿真分析；

5)对弹道导弹进行过载指令限幅，最大过载为10g，对反导导弹进行过载指令限幅，最大过载为30g。

2.1 经典比例导引仿真

对于经典比例导引突防，选择了制导系数为4,5,6分别进行仿真测试。仿真结果如表2～表4所示。

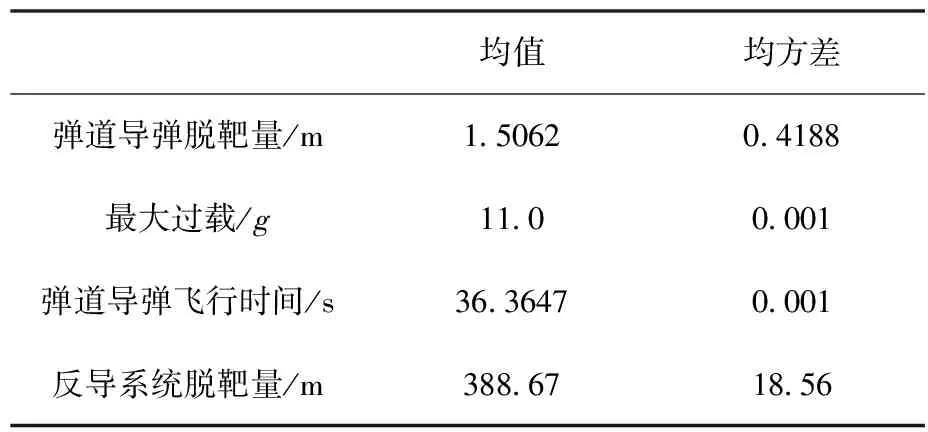
表2 K=4的经典比例导引

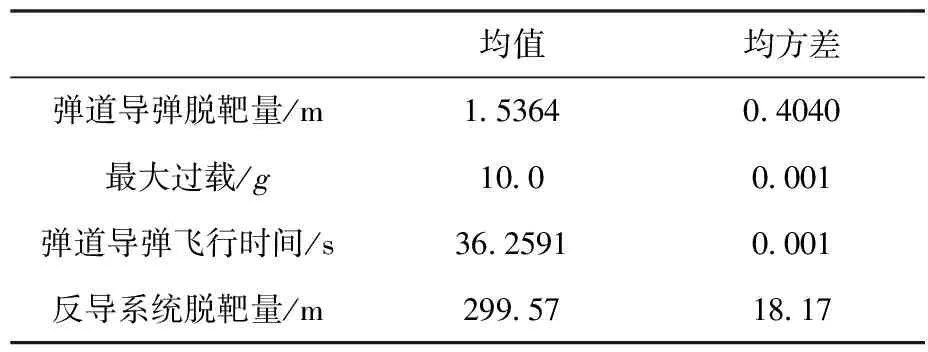
表3 K=5的经典比例导引

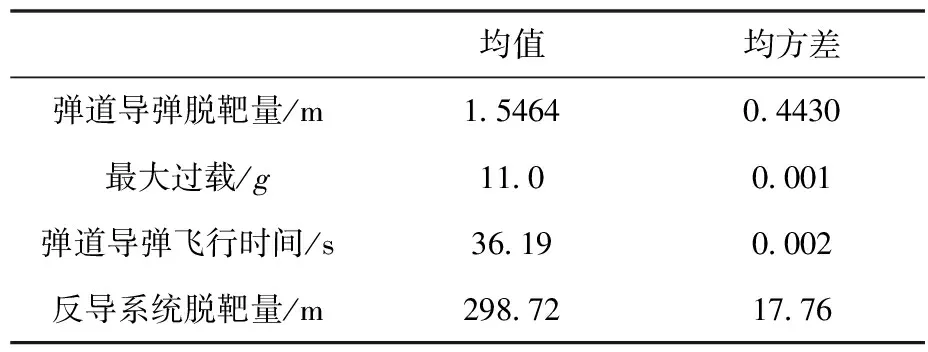
表4 K=6的经典比例导引

2.2 修正比例导引仿真

因为假设弹道导弹攻击的是地面固定目标，所以应用最优控制理论和飞行力学原理，推导出一种以控制能量消耗最小为性能指标，以导弹脱靶量为约束的最优导引律，导引系数的变化不仅与导弹速度大小有关，而且考虑了导弹速度方向的变化。

具体制导律如式(4)所示

(4)

式中

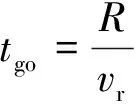
仿真结果如表5所示。

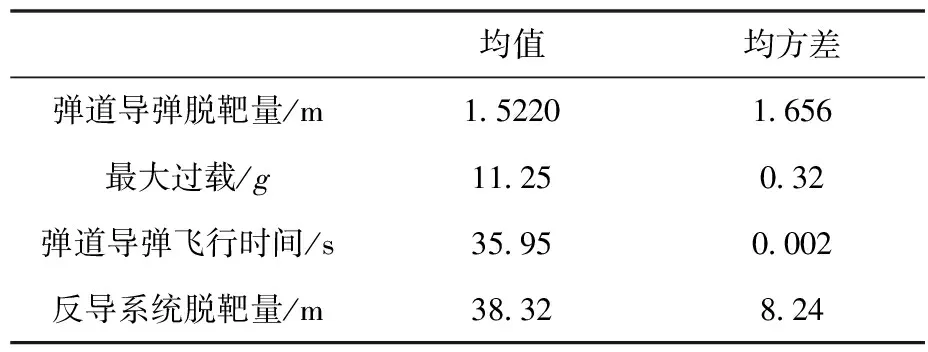
表5 修正比例导引

2.3 变结构比例导引

由于滑模变结构控制具有对参数摄动和外部干扰不敏感的特性，本文针对突防问题，给出过载型式的变结构比例导引律为

(5)

式中，ny表示导弹法向过载指令；ε表示s=0处的趋近速率。

仿真结果如表6所示。

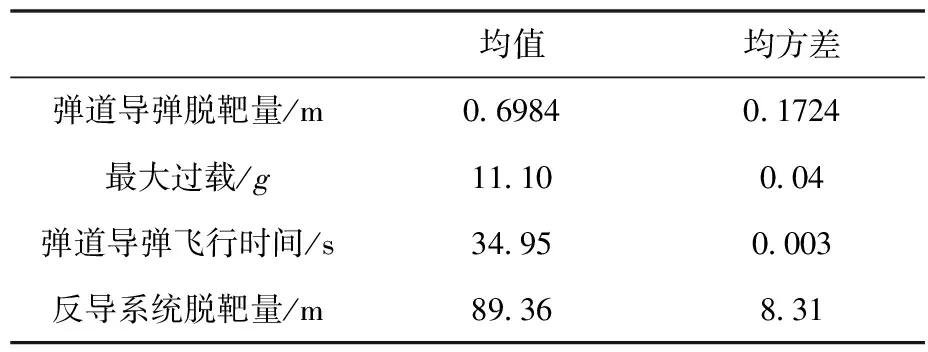
表6 变结构比例导引

3 层次模型分析

通过对性能指标权值矩阵应用归一化方法，继而带入仿真测试结果，计算得出以制导系数为4的经典比例导引为基准的各个导引律性能分数，如表7所示。

表7 性能分数

通过分析仿真结果发现，变结构比例导引的综合突防性能最高，同时经典比例导引突防的性能分数整体高于修正比例导引。这是由于变结构比例导引具有较高的反导脱靶量，同时具有最高的制导精度造成的。而经典比例导引虽然反导脱靶量大，但是制导精度不如变结构比例导引高。修正比例导引的制导精度不高，同时具有较小的反导脱靶量，以致其综合突防性能最低。而四种制导律的最大过载、飞行时间和弹着角三项指标的性能差异不大。

4 结论

通过对随机仿真结果分析发现，从弹道导弹的制导精度角度来说，变结构比例导引具有最高的制导精度，经典比例导引和修正比例导引次之。这是由于变结构比例导引随着末制导时间增加，法向过载以及视线转动角速率趋于零的收敛速率大于经典比例导引和修正比例导引。

而从突防角度来看，经典比例导引弹道较修正比例导引和变结构比例导引弯曲,能充分利用导弹的机动能力，反导导弹脱靶量大，有利于弹道导弹突防。变结构比例导引过载及视线角速率收敛速率大于经典比例导引，故而在弹道导弹突防时，反导导弹将能以较经典比例导引小的脱靶量拦截弹道导弹。修正比例导引，其弹道相对平缓，过载变化范围不大，这使得反导导弹脱靶量小，弹道导弹更易被拦截。

综上所述，由于变结构比例导引是在保证突防的前提下，具有最高制导精度的导引规律，所以在本评估体系中变结构比例导引具有最高的性能分数。由此证明基于层次评估理论所得出的弹道导弹突防制导律性能的优劣与对制导律的理论分析所得出的结果保持一致。因此层次评估理论可以用于弹道导弹末段突防制导律的选择，而合理设置评估体系参数， 有利于对弹道导弹末制导阶段突防制导律的优选。

[1] 李林.弹道导弹弹头机动突防研究[D].哈尔滨工业大学，2011.

[2] 李新国,方群.有翼导弹飞行动力学[M].西安：西北工业大学出版社，2005.

[3] 王亚飞,方洋旺,周晓滨.比例导引律研究现状及其发展[J].火力与指挥控制, 2007,32(10)：8-12.

[4] 程国采.战术导弹导引方法[M].北京：国防工业出版社，1996.

[5] 朴春花.层次分析的研究与应用[D].北京：华北电力大学，2008.

[6] 邓雪，李家铭,曾浩健，等.层次分析法权重计算方法分析及其应用研究[J].数学的实践与认识，2012，42(7)：93-100.

[7] 朱战霞,王建培.一种攻击地面固定目标的变系数比例导引律[J].飞行力学, 2000，18(4)：46-49.

[8] 姚怀瑾,林德福,臧路尧,王武刚.变结构经典比例导引制导性能对比研究[J].计算机仿真, 2014，31(7)：31-35.

Research of Ballistic Missile Penetration Guidance Law at the End of the Trajectory by Using Multiple Stage Analyzing Theory

GE Yun-peng, YANG Jun, YUAN Bo, ZHU Xue-ping

(College of Astronautics, Northwestern Polytechnical University，Xi’an 710072，China)

There is a problem at the end of the trajectory of ballistic missile which is the optimal guidance law of breaking through the defense system.For that problem, we could analyze different guidance laws by using the multiple-stage analyzing theory.As we analyze the means and variances of the precision, the maximum of the overload, the flight time and the precision of the anti-missile, we can assess the performance and importance of the guidance laws.And then, we set up reasonable parameters of the analyzing theory.And after random simulation, we will get the score of different guidance laws by using it.The result of simulation proves that the AHP can be used in choosing and optimizing guidance law at the end trajectory of ballistic missile.

Ballistic missile;Guidance law;Multiple-stage analyzing theory

10.19306/j.cnki.2095-8110.2016.04.008

2015-04-22；

2015-06-23。

葛云鹏(1991-)，男，硕士，主要研究领域为导航制导与控制。E-mail：386159024@qq.com

V448.1

A

2095-8110(2016)04-0042-05