减小双轴旋转惯导中陀螺仪随机漂移影响的方法研究

姜 睿，杨功流，周 潇

(北京航空航天大学 仪器科学与光电工程学院，北京 100191)

减小双轴旋转惯导中陀螺仪随机漂移影响的方法研究

姜 睿，杨功流，周 潇

(北京航空航天大学 仪器科学与光电工程学院，北京 100191)

针对双轴旋转惯导惯性器件的随机误差无法在导航过程中自动进行补偿的问题，提出优化的两位置重调(TPR)的方法来补偿系统的随机误差导致的方位和位置误差，以提高双轴旋转惯导的长航时精度。与传统两位置重调(CPR)方法相比，使用优化的误差传递方程的两位置重调的方法，可以在少于6h条件下估计出系统的方位误差，从而使得系统的位置精度和方位精度都得以极大的提高。根据惯性器件的随机误差导致的方位误差的特性，建立了TPR的误差模型。通过仿真，证明了该方法的有效性。

两位置重调；双轴旋转；随机误差

0 引言

双轴旋转惯导起源于旋转式惯性单元技术[1]，该技术可以通过旋转的方法在短期内平均惯性测量单元的漂移。双轴旋转惯导具有高精度和低成本的特点，因此广泛地被北大西洋公约组织和美国用于海面舰艇和潜艇导航中[2-3]。很多研究都集中在如何提高双轴旋转惯导的精度。文献[4]介绍了双轴旋转的转位方案，自标定技术。文献[5]提出了重调方法。文献[6]给出了16位置旋转方案，该旋转方法可以补偿所有陀螺仪的漂移并且不会引入其他累积的系统误差。文献[7]讲解了包括误差传递特性和转位方案设计在内的双轴旋转惯导的关键技术。文献[8]讨论了双轴旋转惯导的转动引起的误差。

上面提到的技术和方法解决了很多双轴旋转惯导在实际应用中出现的问题。为了进一步提高精度，还需要对重调技术进行研究。对于普通的惯导，陀螺仪的随机误差将造成位置误差和方位误差，只有位置误差可以通过传统的重调技术(CPR)进行补偿[9]。实际上，通过优化姿态误差模型，位置误差和方位误差可以同时得到补偿。本文在推导双轴旋转惯导误差传递方程的基础上，提出改进的两位置重调的方法，用于在4～6h之间任何一点修正由陀螺随机漂移引起的方位误差和位置误差，并且根据提出的方案进行了仿真验证。

1 双轴旋转惯导的误差建模

双轴旋转惯导仍然属于捷联式惯导的范畴，因此其误差方程和捷联式惯导的误差方程总体上是一样的[10]。误差传递方程的推导有两种途径：ψ角误差模型和Ф角误差模型[11-12]。本文使用ψ角误差模型来描述双轴旋转惯导误差传递特性。

(1)

(2)

(3)

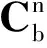
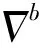
εb=bg+Sgωb+Ngωb+Kgfb+νg

(4)

(5)

式中，bg为陀螺常值偏置 ，ba为加速度计比例偏置，Sg为陀螺仪比例因素误差矩阵，Sa为加速度计比例因素误差矩阵，Ng、Na为不对准误差矩阵，Kg代表与g有关项偏移系数矩阵。fb是作用在载体坐标系下的外力。νg、νa是随机误差。载体坐标系是正交坐标系，陀螺仪坐标系与载体坐标系之间关系如图1所示。

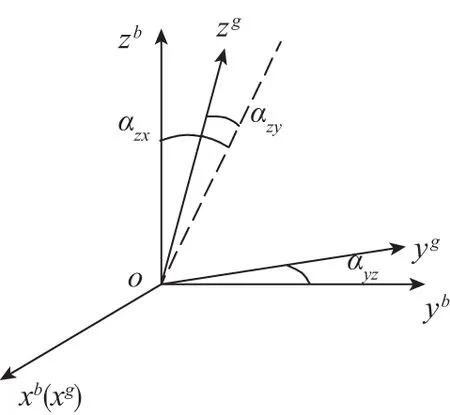
图1 载体坐标系与陀螺仪坐标系之间的关系Fig.1 Relationship between the body frame (b frame) and the gyro frame(s frame)

xb与xg一致，yb在ygxg平面内，zb与xb、yb满足右手定则。

由于不对准角是小角，陀螺仪的不对准误差矩阵可以写为

(6)

同样，加速度计敏感轴与陀螺仪敏感轴之间的不对准误差矩阵可以写为[7]

(7)

2 两位置重调

重调(PR)是船用惯导系统特有的一项关键技术，借助准确的外界辅助信息(如卫星定位信息、天文导航姿态信息等)对惯导系统误差进行修正。重调期间，需要提供位置信息才可以进行惯导系统相关参数的校正。虽然陀螺仪的随机误差会引起方位误差和位置误差，但通常在传统的重调方法(CPR)中会忽略方位误差[10]。

本节将研究陀螺仪随机漂移引起的方位误差，并提供用于双轴旋转惯导随机误差补偿的两位置重调的方法。与传统的位置重调法相比，两位置重调可以同时估计和补偿方位误差和位置误差。

2.1 陀螺仪随机漂移引入的方位误差的特性

在第1节中提到，惯导误差传递方程有两种表达方法，一种基于ψ角，一种基于Ф角。两者之间的关系如下[8]

Φn=δθn+ψn

(8)

其中，Φn是Φ角误差，ψn是ψ角误差。δθn是位置角误差，可用式(9)表达为

(9)

式中，L为当地纬度，δL为纬度误差，δλ为经度误差。

与g有关项偏置，比例因数误差和不对准误差等常值误差可以通过标定确定[11-15]。则传感器的误差模型可以简化为:

(10)

由双轴旋转惯导的原理[3,5]可知，式(4)和式(5)中的bg和ba两项会被调制平均，所以在双轴旋转惯导中，陀螺仪的随机漂移成为主要的误差源。式(1)可以改写为式(11)。

(11)

陆上、海面和水下载体都是长时间的导航，能达到几天甚至几个月以上，通常使用速度阻尼的方法减少舒勒周期对导航误差的影响。横摇角和纵摇角误差能得到很大程度的降低[16]。但是，速度阻尼却不能有效地减小方位角误差。

2.2 两位置重调的方法

为了估计和修正方位角误差以及由随机误差引入的位置误差，提出一个优化的重调方法，即两位置重调。该方法包含两步:

1)在第一个位置信息可用的时候，重置系统的位置；

2)估计并修正方位误差直到第二次位置信息可用的时候，并重置位置信息。

两位置重调的具体方法如下:

(12)

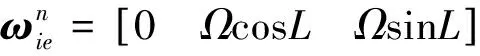
(13)

通常，陀螺仪的随机误差将缓慢地、累积性地影响在特征周期(T0=24h)中的ψ角的传递特性。因此，对于双轴旋转惯导系统，在陀螺常值漂移误差被调制掉后，需要校正由陀螺仪的随机误差引起的位置和方位误差。典型的ψ角误差中方位角误差的增长如图2所示。

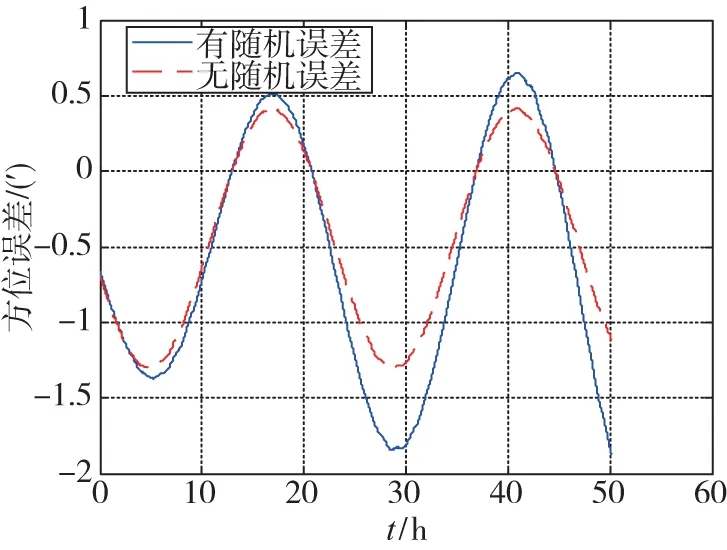
图2 ψ角方位误差的传递特性Fig.2 Propagation characteristic of an azimuth error of the psi-angle

在两次重调之间有4～6h(传统重调是6h)，比特征周期短了很多，由随机误差引起的误差累积很小。因此，在两次重调之间，可以用不包含随机误差的方位误差曲线拟合包含随机误差的方位误差曲线，拟合精度在短时间内是满足要求的。

根据含有随机误差的式(12)，不含随机误差的式(14)如下

(14)

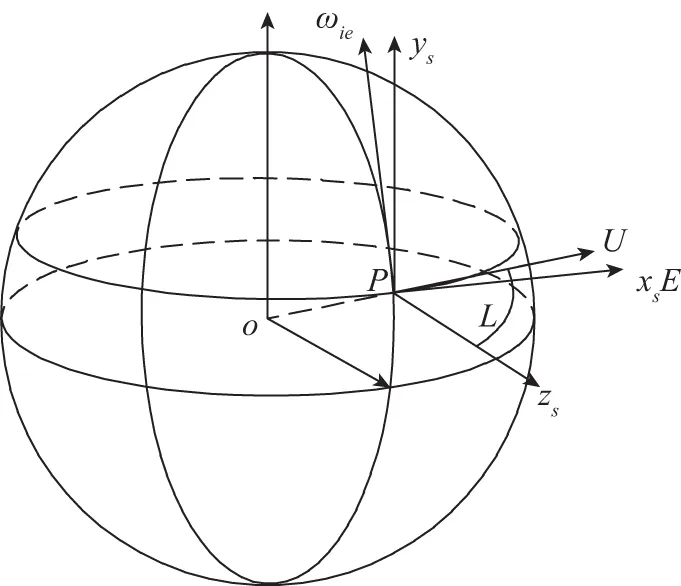
图3 S坐标系与导航坐标系之间的关系Fig.3 Relationship between the gyro frame(S frame) and the navigation frame

S坐标系到导航坐标系n的方向余弦矩阵是

(15)

则S坐标系下的ψ角可以表示为

(16)

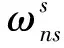
(17)

式(17)的解析解为

ψt(t)=T(t,t0)·ψs(t0)

(18)

其中

(19)

由于速度阻尼能显著地减小纵摇角和横摇角的误差，以在两次重调期间，纵摇角和横摇角的误差接近于零。因此式(8)可以简化为：

(20)

将式(8)、式(9)和式(17)带到式(20)中得到

(21)

根据第一个位置的信息，式(18)可以重新编辑作为第一次重调的式(22)

(22)

同理，第二次重调时经纬度误差和方位角为

(23)

因此，两个重调点之间的关系为:

(24)

需要注意的是，这里有三个假设条件：

1)纵摇角误差和横摇角误差为零；

2)陀螺仪的常值偏移误差经过调制；

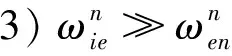
实际上，在整个重调期间，这些假设不是都能成立。但是在低速和小机动的情况下，两位置重调可以估计出满足使用的方位误差。通过仿真可以验证这一点。

3 两位置重调的仿真计算

为了证明所提出的两位置重调方法的优势，将传统重调也同时进行仿真以作为比对。仿真条件如下:

1)初始对准姿态误差(0′,0′,1.8′)；

3)两次重调分别在第20个小时和第26个小时；

4)系统的导航过程中有速度阻尼。

仿真结果如图4和图5所示。图4是在速度阻尼的情况下进行两位置重调和传统重调时方位误差的比对图。图5是在速度阻尼的情况下进行两位置重调和传统重调时位置误差的比对图。两个方法都在第20个小时对位置误差进行修正。在第26个小时，包含ψ角误差和位置误差的方位误差(φ角误差)通过两位置重调得到补偿，而传统的重调只补偿了位置误差。

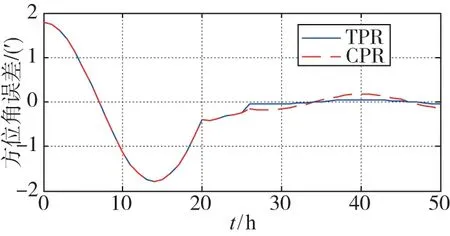
图4 传统重调和两位置重调方位误差Fig.4 Azimuth errors by using the TPR method and by using the CPR

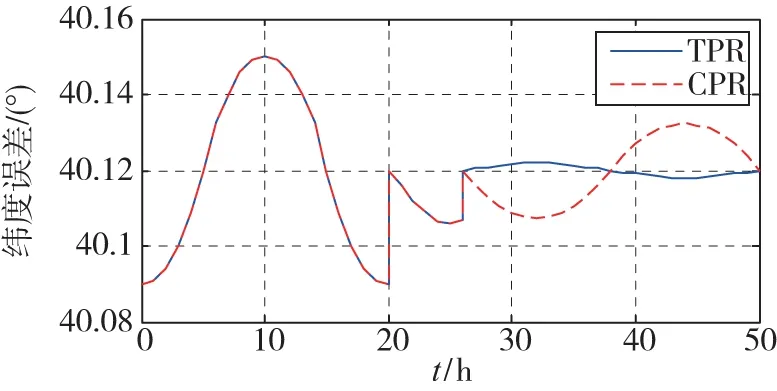
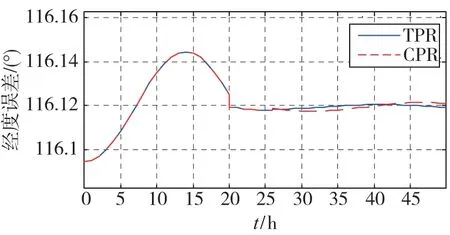
图5 速度阻尼下两种方法经度和纬度误差对比Fig.5 Latitude and lontitde error with velocity damping by using the TPR method and by using the CPR method

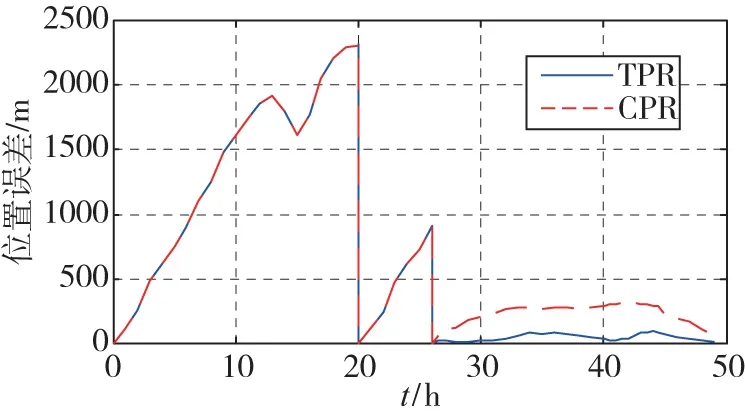
图6 速度阻尼下两种方法位置误差对比图Fig.6 Position output with velocity damping by using the TPR method and by using the CPR method

图6是有速度阻尼时，传统重调和两位置重调下的位置圆概率误差对比图。从图6中可以看出，使用两位置重调，位置圆概率误差小于90m。使用传统重调，位置圆概率误差大于300m。

根据上面的对比可以得到这样的结论，在相同的仿真条件下，使用两位置重调时，方位误差和位置圆概率误差都优于传统的重调方法。

4 结论

为了提高双轴旋转惯导在长航时的系统精度，降低陀螺仪随机游走对位置精度的影响，本文提出了两位置重调的方法。该方法在以下方面取得了明显的效果：

1)利用两点位置信息，同时修正惯导系统位置误差和方位误差；

2)由于方位误差是通过计算公式估计，因此两位置修正时间间隔不受6h限制，一般选择4～6h，极大地提高了舰艇的安全。

[1]FinckeWH.StrapdownInertialSensingUnitRotation/SISUR/-Anewapproachtoinertialnavigation[C]//IEEE1978PositionLocationandNavigationSymposium, 1978: 132-145.

[2]TittertonD,WestonJL.Strapdowninertialnavigationtechnology[M].IET, 2004.

[3]LevinsonE,MajureR.Accuracyenhancementtechniquesappliedtothemarineringlaserinertialnavigator(MARLIN)[J].Navigation, 1987, 34(1): 64-86.

[4]LevinsonE,GiovanniCS.Lasergyropotentialforlongendurancemarinenavigation[C]//IEEEPositionLocationandNavigationSymposium, 1980: 115 -129.

[5]YuanB,LiaoD,HanS.ErrorcompensationofanopticalgyroINSbymulti-axisrotation[J].MeasurementScienceandTechnology, 2012, 23(2): 025102.

[6]YinH,YangG,SongN,etal.Errormodulationschemeanalyzingfordual-axisrotatingfiber-opticgyroinertialnavigationsystem[J].SensorLetters, 2012, 10(7): 1359-1363.

[7]SongN,CaiQ,YangG,etal.Analysisandcalibrationofthemountingerrorsbetweeninertialmeasurementunitandturntableindual-axisrotationalinertialnavigationsystem[J].MeasurementScienceandTechnology, 2013, 24(11): 115002.

[8]Goshen-MeskinD,Bar-ItzhackIY.Unifiedapproachtoinertialnavigationsystemerrormodeling[J].JournalofGuidance,Control,andDynamics, 1992, 15(3): 648-653.

[9]BensonJrDO.Acomparisonoftwoapproachestopure-inertialandDoppler-inertialerroranalysis[J].AerospaceandElectronicSystems,IEEETransactionson, 1975 (4): 447-455.

[10]BonaBE,SmayRJ.Optimumresetofship'sinertialnavigationsystem[J].AerospaceandElectronicSystems,IEEETransactionson, 1966,2(4): 409-414.

[11]SyedZF,AggarwalP,GoodallC,etal.Anewmulti-positioncalibrationmethodforMEMSinertialnavigationsystems[J].MeasurementScienceandTechnology, 2007, 18(7): 1897.

[12]NieminenT,KangasJ,SuuriniemiS,etal.Anenhancedmulti-positioncalibrationmethodforconsumer-gradeinertialmeasurementunitsappliedandtested[J].MeasurementScienceandTechnology, 2010, 21(10): 105204.

[13]FongWT,OngSK,NeeAYC.Methodsforin-fieldusercalibrationofaninertialmeasurementunitwithoutexternalequipment[J].MeasurementScienceandTechnology, 2008, 19(8): 085202.

[14]ZhangH,WuY,WuW,etal.Improvedmulti-positioncalibrationforinertialmeasurementunits[J].MeasurementScienceandTechnology, 2009, 21(1): 015107.

[15]LiY,NiuX,ZhangQ,etal.Aninsituhandcalibrationmethodusingapseudo-observationschemeforlow-endinertialmeasurementunits[J].MeasurementScienceandTechnology, 2012, 23(10): 105104.

[16] 高钟毓. 惯性导航系统技术[M]. 北京：清华大学出版社, 2012.

Research on Reducing the Influence of Stochastic Error of Gyros in a Dual-Axis Rotational Inertial Navigation System

JIANG Rui,YANG Gong-liu,ZHOU Xiao

(School of Instrumentation Science and Opto-electronics Engineering, Beihang University, Beijing 100191, China)

The stochastic errors of inertial sensors in a dual-axis rotational inertial navigation system are not averaged out automatically during navigation. Therefore an optimized Twice Position-fix Reset (TPR) method is provided to enhance accuracy of a dual-axis rotational INS by compensating stochastic errors. Compared with Conventional Position-fix Reset(CPR) method, both an azimuth error and a radial-position error are extremely corrected within 6 hours by the TPR method. An optimized error propagation equation has built on the characteristics of an azimuth error introduced by stochastic errors of an inertial sensor. As the result, accuracy of the system is prominently enhanced, as is verified by simulation.

Twice position-fix reset; Dual-axis rotation; Stochastic error

10.19306/j.cnki.2095-8110.2016.04.005

2016-04-20；

2016-05-23。

姜睿(1975-)，女，硕士，主要从事惯性技术的研究。E-mail：Buaajr@163.com

U666.1

A

2095-8110(2016)04-0025-05