光学遥感卫星对月定标时姿态机动补偿方法

高涵 白照广 陆春玲 邸国栋

(航天东方红卫星有限公司，北京 100094)

光学遥感卫星对月定标时姿态机动补偿方法

高涵 白照广 陆春玲 邸国栋

(航天东方红卫星有限公司，北京 100094)

对月定标具有不依赖地面定标场、不受天气影响、定标效率高等优势，但需要解决对月姿态控制及成像参数匹配性设计问题。文章针对光学遥感卫星推扫成像，提出一种姿态机动补偿方法，用于解决星载相机对月成像过程中积分时间与推扫速度失配的问题，并以一颗太阳同步轨道卫星作为分析对象，研究了卫星对月成像时的补偿角速度，经过对姿态机动补偿过程进行仿真分析，结果表明：使用该方法可以使相机推扫速度与积分时间匹配，达到正常对月成像的目的。

时间延迟积分CCD；对月成像；姿态机动补偿

1 引言

卫星发射前后，为获取精确的星上遥感器辐射特性和辐射响应变化，需要对星上的敏感器件进行辐射定标工作。我国遥感卫星的在轨定标目前仍以地球表面真实景物目标为主，精度受大气环境影响较大，定标频次较低。利用空间天体进行在轨辐射定标可以消除大气层影响，提高定标频次。在天体定标中，对日定标有比较广泛的应用；但由于太阳光太强，超出遥感器动态范围，需要采用漫射板反射太阳光线，而漫散板长期暴露在宇宙空间辐射中，极易受到污染，引起性能退化，不适于长寿命遥感卫星。天体定标方法中，对月定标成为国际上研究的热门。

月球是除太阳外所能观察到的最大的光源，依靠反射太阳而发光，其光谱特性与太阳光谱的自身吸收、反射有关，稳定性好，且光强一般在遥感器动态范围内，可将遥感器直接对月成像。采取对月成像的方式，可以对卫星大部分光学遥感仪器定标，在获取标准月球辐照度模型的情况下(如美国的ROLO模型)，利用月球进行绝对辐射定标需要精确地计算出观测角度和天体距离等的影响，并获取准确的月球光谱分布，可实现高定标精度，适合长寿命遥感卫星。

对月定标不受大气影响，在地影区进行成像，不影响陆地成像，可增加定标次数。将月球作为稳定辐射源，定标时机的选择与相机本身参数和月相有关，定标时间选择范围增加，可以提高定标频率和定标精度，拓宽定标时机的选择面。

目前，遥感卫星对月成像方式为：通过控制卫星的初始姿态角实现相机光轴对月球定向后，利用卫星绕地球轨道的运动实现对月绝对定标成像，在定标过程中，卫星整星姿态不采取修正措施。获取的月球图像模糊不清，甚至无法辨识。产生模糊的原因是相机的积分时间与光轴在月球表面的推扫速度失配引起的过采样[1-4]。过采样情况下相机光生电荷无法正常读出，成像调制传递函数(MTF)将下降，直接造成对月定标精度降低。因此过采样问题是对月定标过程须解决的首要难题。

目前，解决过采样问题有两种方法：第一种针对早期的线阵CCD相机，采用地面数据处理的方式还原畸变图像[5]；第二种针对高精度的TDICCD相机，采用技术或设备使得相机积分时间宽幅可调。文献[6]中的中分辨率光谱成像仪(MODIS)遥感器就是采用地面数据处理的方式还原畸变图像；文献[7]叙述了我国风云二号卫星利用月球进行内黑体定标的过程，星上可见光-红外自旋扫描辐射计(VISSR)遥感器与MODIS类似，也通过地面数据处理对畸变图像进行配准补偿；文献[8]中的昴宿星(Pleiades)卫星，使用TDICCD相机对月成像，该相机具有较大的积分时间可调范围(0.3～3 ms)。上述两种方法适用性单一，且存在一定缺陷或难度：采用地面处理的方式只能还原普通线阵CCD相机的畸变图像，会造成图像精度降低，影响定标精度，且该方法对于TDICCD相机并不适用；增加积分时间可调范围的方法可以有效解决TDICCD相机对月定标的过采样问题，但需要兼顾曝光量的饱和值与相机信噪比的关系，对设备的性能要求较高，同时该方法不能够用于普通线阵CCD相机。

本文针对上述问题，提出采用姿态机动补偿TDICCD相机推扫速度的方法，在不额外增加仪器、不改变原有扫描行周期的情况下，仅通过对卫星姿态角速度的控制增加卫星推扫速度，使得推扫速度与积分时间匹配，完成对月定标工作。此方法不但可以用于TDICCD相机，对于普通线阵CCD相机同样适用。

2 卫星姿态机动补偿方法

2.1 成像方式分析与补偿角速度分析

卫星对月成像过程中，相机光轴需要对月球惯性定向，进而对月球推扫成像。TDICCD相机成像时需要沿积分方向推扫[9]。由于卫星距月球较远，卫星对月成像时间很短，在成像过程中可以假设月球静止，同时令卫星的偏航角始终保持为零。根据上述特性及分析结果，提出两种成像方式：第一，卫星先进行滚转机动，相机光轴由指向地面转到指向空间，再通过俯仰机动，令光轴对月球定向，见图1，此时相机光轴推扫方向与卫星沿轨道运动方向相同；第二，卫星先进行俯仰机动，相机光轴由指向地面转到指向空间，再进行滚转机动，使光轴对准月球，见图2，此时相机光轴推扫方向与卫星沿轨道运动方向相反。两种机动方式中，相机推扫成像方向与卫星沿轨道运动方向的差异会引起对月推扫补偿角速度的差异。

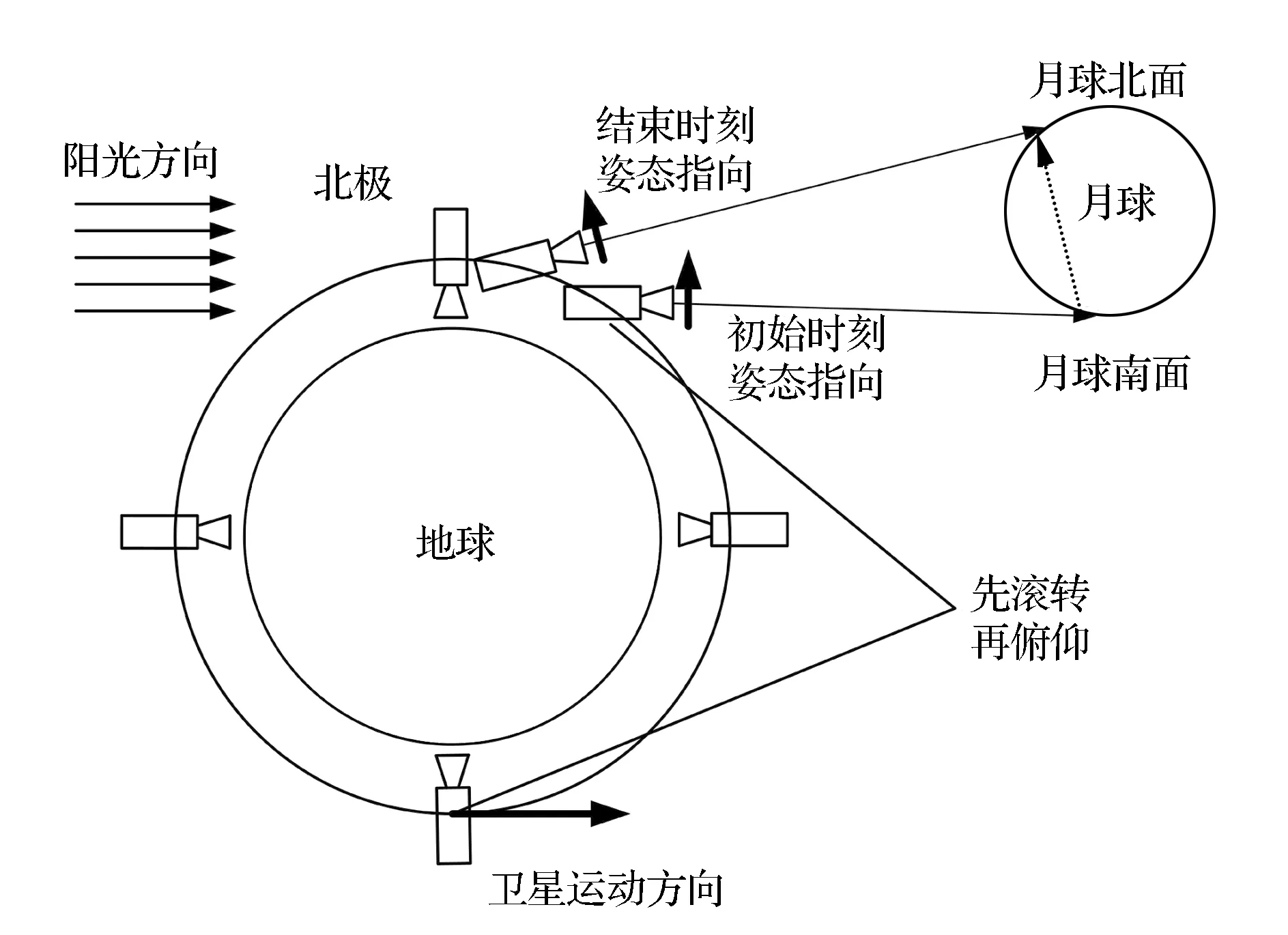
图1 采用第一种方式成像(推扫方向与运动方向相同)Fig.1 Lunar imaging using the first method (scanning direction is the same as motion direction)

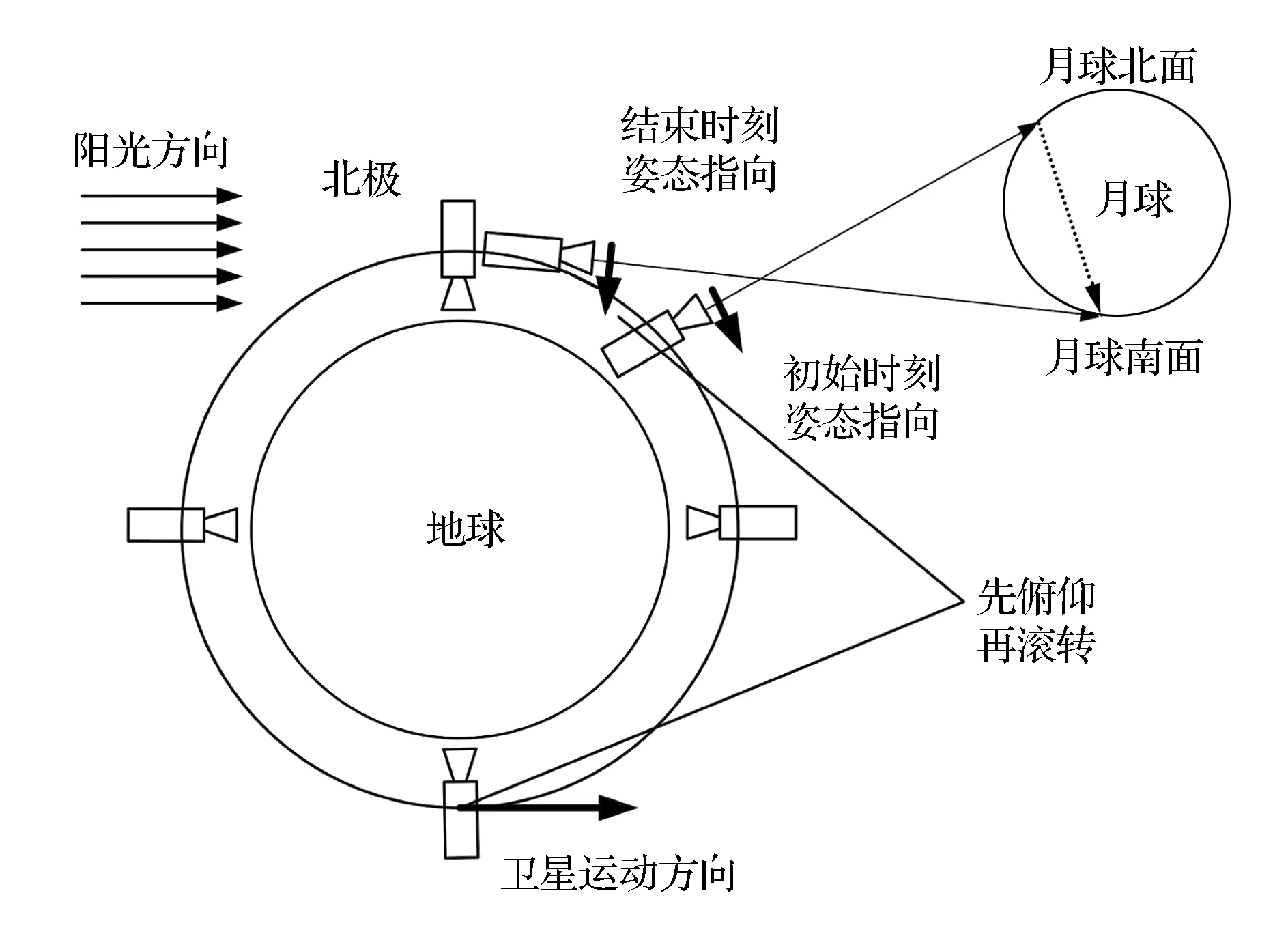
图2 采用第二种方式成像(推扫方向与 运动方向相反)Fig.2 Lunar imaging using the second method (scanning direction is opposite to motion direction)

使用两种不同的成像方式，卫星绕地球运动实现对月成像，成像方向与对地成像相同，与卫星滚动轴同向，与俯仰轴垂直，如图3所示，此时卫星视轴推扫速度过慢，景物不能按正确的行周期进入下一级敏感单元，引起多帧图景的重叠覆盖，即过采样情况；如果保证偏航角不变，对卫星施加俯仰机动，如图4所示进行俯仰机动补偿后，卫星推扫速度加快，景物可以依次进入下一级敏感单元，即利用卫星绕俯仰轴的姿态机动达到补偿推扫速度的目的，令相机积分时间与光轴在月球表面的推扫速度匹配，从而解决过采样问题。

使用姿态机动的方法对推扫速度进行补偿时，须要计算补偿角速度和成像时刻卫星姿态角，补偿角速度通过卫星轨道参数和成像参数计算；成像时刻姿态角须要建立卫星姿态运动学模型求取，因此要根据卫星本身的成像特性对补偿情况进行分析计算。首先计算卫星轨道参数和成像参数[10]。

卫星的星下点地速为

(1)

地面采样距离为

(2)

积分时间为

(3)

式中：Vn是星下点地速，R=6 371.004 km，a是轨道半长轴，μ为地球引力常数，DGSD为地面采样距离，H为轨道高度，d为像元尺寸，f′为相机焦距。

由于卫星和月球距离较远，忽略卫星在轨运动时卫星和月球间的距离变化，取卫星处于地月连线附近时卫星和月表之间的距离作为定标时的距离，根据卫星成像参数与轨道参数，计算得到补偿俯仰角速度为

(4)

式中：S表示地月距离，Rm为月球半径，V是与积分时间相匹配的推扫速度，v是卫星在轨运行时光轴在月球表面的投影线速度。当卫星采用第一种方式对月成像时，式(4)中取减号；采用第二种方式对月成像时，式(4)中取加号。

图3 姿态机动补偿前卫星对月成像图示Fig.3 Lunar imaging without the attitude maneuver compensation

图4 姿态机动补偿后卫星对月成像图示Fig.4 Lunar imaging with the attitude maneuver compensation

2.2 卫星姿态运动学建模

已知卫星的补偿角速度，根据卫星对月成像方式建立卫星姿态运动学模型，求取卫星对月定标各个时刻的姿态，选取不同时刻的姿态进行机动补偿。建立如图5中成像几何模型，引入如下坐标系。

(1)地心惯性坐标系Oi-XiYiZi：即地心赤道惯性系，其原点O在地心，Xi轴指向春分点，Zi轴垂直于赤道面指向北极，Yi轴由右手法则确定。

(2)卫星轨道坐标系Oo-XoYoZo：也称为相对运动坐标系，其原点Oo在航天器质心，Xo轴指向航天器前进方向，Zo由航天器质心指向地心，Yo轴垂直于Xo和Zo构成的轨道平面，按右手法则确定。

(3)卫星本体坐标系Ob-XbYbZb：原点Ob在卫星质心，Xb，Yb，Zb三个坐标轴固定在航天器本体上，三个坐标轴和星体主惯量轴一致。

下面是三个坐标系之间相互转换关系：

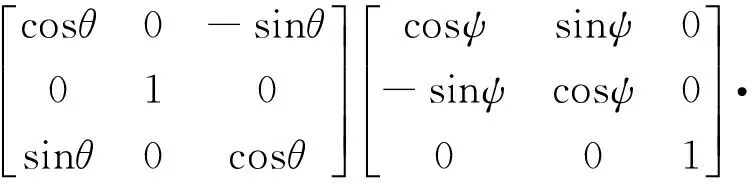
(5)

式中：Cbo表示卫星轨道坐标系到卫星本体坐标系的转换关系，Coi表示惯性系到卫星轨道坐标系的转换关系。R为地球半径，H为卫星轨道高度，i0为轨道倾角，u表示纬度幅角，u=w+f，w为近地点幅角，f为真近点角，其中Ω为卫星轨道的升交点赤经；ψ，φ，θ表示成像时偏航、俯仰和滚转角。

图5 对月成像几何模型Fig.5 Lunar imaging geometric model

预先给定卫星每次成像的起始时间，计算卫星每次成像开始时的姿态角，方法如下：在地心惯性坐标系Oi-XiYiZi中，根据卫星轨道和月球星历确定每次成像的成像卫星与月球之间的位置矢量p，p即卫星本体坐标系Zb的指向，将惯性坐标系中的位置矢量p转换到卫星本体坐标系Ob-XbYbZb中，在三轴进行投影得到p=[p1p2p3]T。

月球星历采用JPL星历表，JPL星历表是由美国喷气推进实验室(JPL)依据最新确定的天文常数和天体运动理论计算的各大行星、太阳、地球及月球的相对位置、速度、黄经章动和月球物理天平动及其变率的数值[11]。根据角度关系求得任意成像开始时刻的卫星姿态角如下。

(6)

(7)

ψ=0°

(8)

3 仿真分析

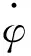
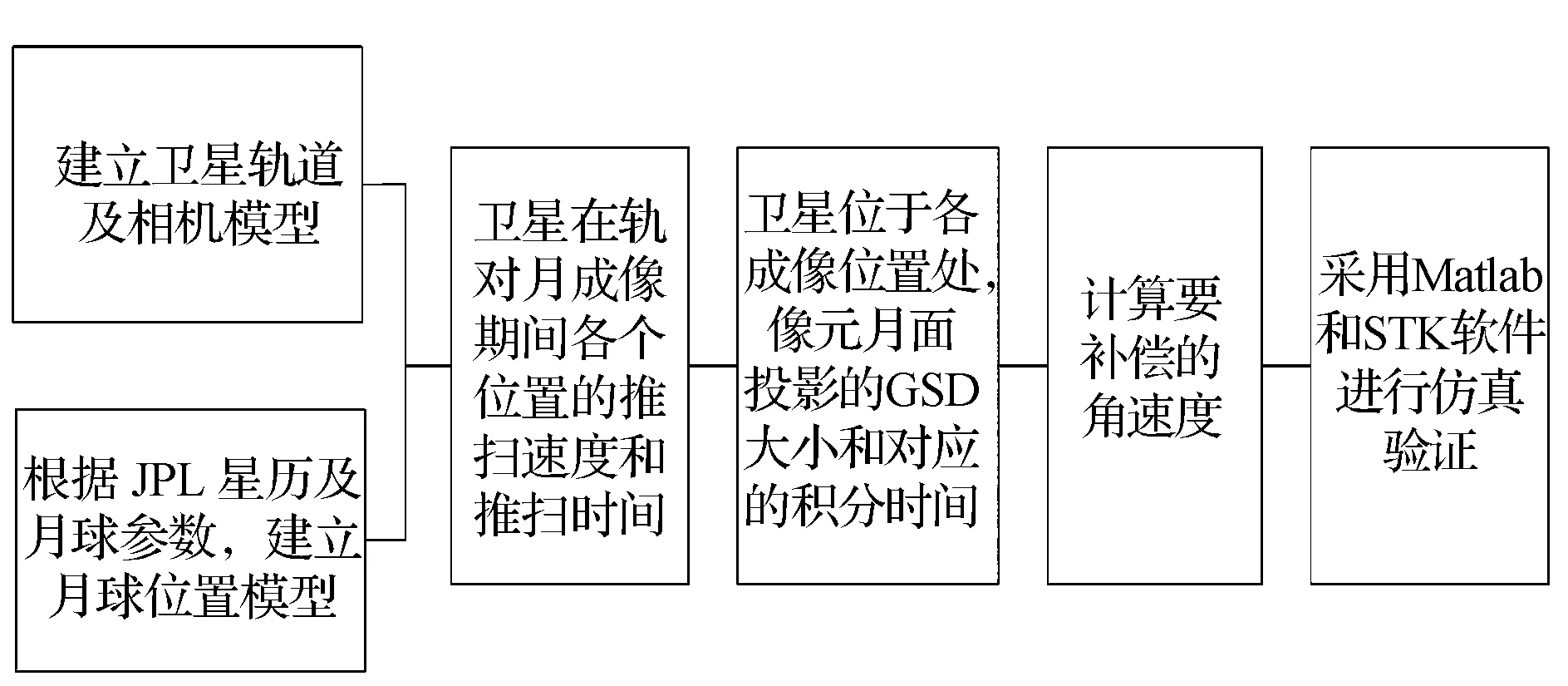
图6 姿态机动补偿建模与仿真流程图Fig.6 Flow chart of modeling and simulation for attitude maneuver compensation

3.1 卫星补偿角速度仿真分析

为了验证姿态补偿效果，仿真过程中使用Matlab软件和STK软件，通过Matlab软件获取仿真数据，并进行数据分析；利用Matlab软件控制STK软件进行交互，直观观察补偿过程。设卫星轨道高度为650 km，TDICCD相机像元尺寸d=8.75 um，焦距f′=2850 mm。根据式(1)～(3)计算得到，卫星星下点地速为Vn=6.845 km/s，地面像元投影尺寸DGSD=2 m，积分时间Tint=0.289ms。仿真结果中x轴和y轴分别为卫星运行时间和卫星与月球距离，卫星从南极到北极半圈轨道的运行时间0～3000s，卫星与月球距离按照星历输入。

通过图7～图10可以看出：

(1)卫星在无补偿的情况下，各个时刻光轴在月球表面投影线速度随星月距离和卫星运行时间的变化而变化，设沿卫星运动方向推扫时速度为正，该数值-37.2km/s～442.7km/s，见图7。产生负值的原因是由于黄白交角的存在。

(2)如图8和图9所示，卫星采用两种不同的成像方式时， 补偿角速度从两极到赤道的变化规律正好相反，在赤道和两极附近分别取得最大或最小值，因此在进行任务规划时，可以根据该变化规律选择补偿角速度最小的位置进行定标，从而节省机动时间。两种成像方式下，卫星的补偿角速度变化范围分别为0.505 1(°)/s～0.667 5(°)/s(第一种)和0.557 2(°)/s～0.728 8(°)/s(第二种)，从补偿角速度的大小来考虑，第一种成像方式需要的补偿角速度较小，对姿态控制要求较低，更适合进行对月成像工作。

(3)姿态机动补偿前后光轴在月表投影线速度存在较大差异，见图10，黑色和白色曲面分别代表姿态机动补偿前后卫星遥感器光轴在月表投影线速度随星月距离和时间的变化关系，补偿后的线速度从3 726.9km/s～4 389.6km/s，是补偿前线速度-37.2km/s～442.7km/s的近10倍。

图7 卫星无补偿时光轴在月表投影线速度 随星月距离和时间变化关系示意图Fig.7 Projection linear speed of optical axis on moon versus time and the distance between satellite and the moon without compensation

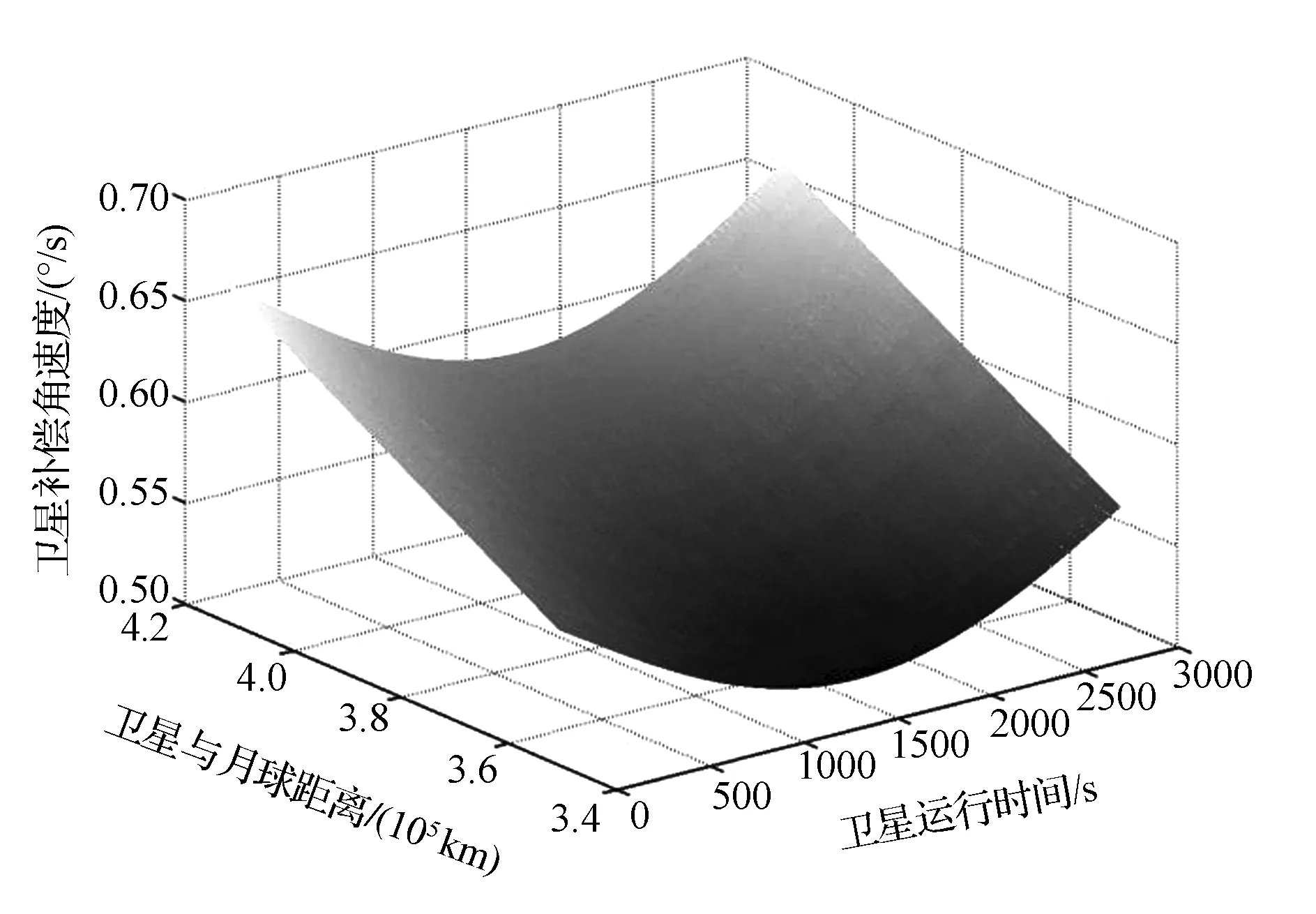
图8 采用第一种成像方式的补偿角速度 随星月距离和时间变化关系示意图Fig.8 Compensation angular velocity for lunar imaging versus time and the distance between satellite and the moon using the first imaging method

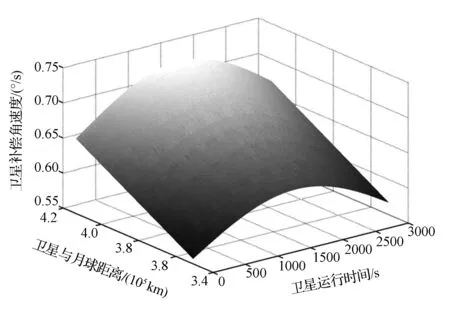
图9 采用第二种成像方式的补偿角速度随 星月距离和时间变化关系示意图Fig.9 Compensation angular velocity for lunar imaging versus time and the distance between satellite and the moon using the second imaging method

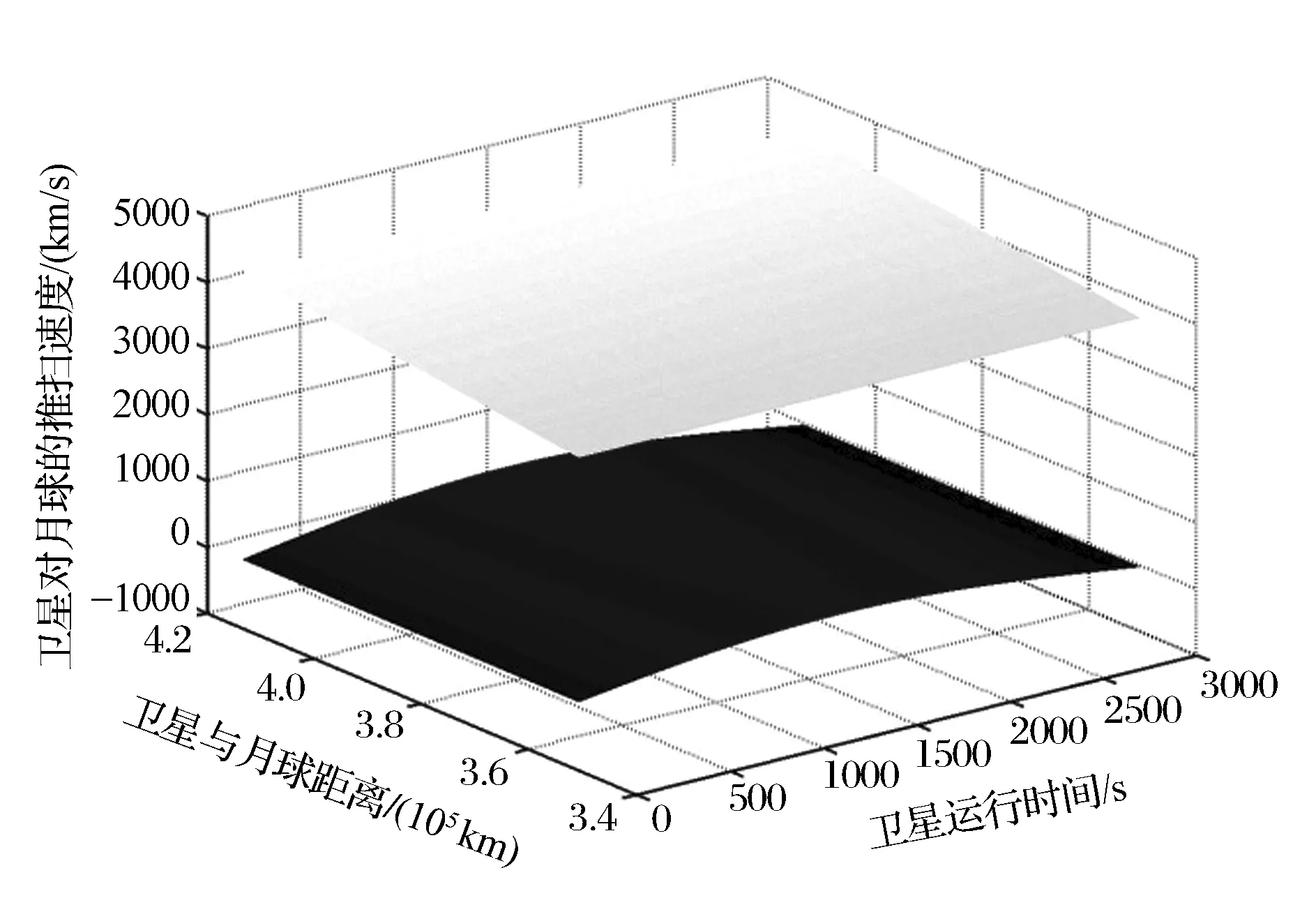
图10 补偿前后卫星遥感器光轴在月表投影线 速度随星月距离和时间变化关系的对比图Fig.10 Comparison of projection linear speed of optical axis on moon versus time and distance between satellite and the moon before and after compensation

3.2 补偿过程姿态角仿真分析

按照月球接近满月时，选取仿真时刻2018-03-29T10：11：30.000，分别采用两种成像方式成像，下面是采用两种成像方式成像时，姿态机动补偿前后卫星姿态角变化情况。

从图11～图14可以看出：

(1)对月成像过程时间较短，整个过程用时约1 s，因此设月球在定标期间位置保持相对静止符合实际情况，在对月定标过程中预设偏航角保持不变，始终为0°，成像过程中只补偿俯仰角，因此滚动角也不发生变化。

(2)卫星采用第一种成像方式，未补偿前在成像时间内，俯仰角10.51°～10.56°(见图11)，卫星视场从月球边缘向中心沿积分方向推扫0.054°，补偿后俯仰角10.51°～10.01°(见图12)，卫星视场从月球边缘向中心沿积分方向推扫0.52°；采用第二种成像方式，未补偿前在成像时间内，俯仰角168.99°～168.94°(见图13)，卫星逆积分方向推扫0.051°，补偿后俯仰角从168.99(°)/s～169.51(°)/s(见图14)，卫星沿积分方向推扫0.53°；在不采用姿态机动补偿的情况下，第二种成像方式根本无法成像。

(3)采用第一种成像方式时，卫星定标时姿态角为[0° 10.51° 174.34°]，采用第二种成像方式时为[0° 168.45° 20.18°]，从达到预定姿态角的总机动角度来考虑，应选取总机动角度较小的第一种成像方式，而从补偿角度考虑也应该选择补偿角速度较小的第一种成像方式。

图11 采用第一种成像方式未进行姿态机动 补偿时的姿态角变化Fig.11 Changes of attitude angle versus time using the first imaging method without attitude maneuver compensation

图12 采用第一种成像方式进行姿态机动 补偿后的姿态角变化Fig.12 Changes of attitude angle versus time using the first imaging method with attitude maneuver compensation

图13 采用第二种成像方式未进行姿态机动 补偿时的姿态角变化Fig.13 Changes of attitude angle versus time using the second imaging method without attitude maneuver compensation

图14 采用第二种成像方式进行姿态机动 补偿后的姿态角变化Fig.14 Changes of attitude angle versus time using the second imaging method with attitude maneuver compensation

3.3 卫星场景仿真

为了更好地模拟真实遥感卫星成像特点，在STK中建立仿真场景，选择650 km太阳同步轨道卫星(见图15)，选取一般国内遥感卫星可见光成像时间较好的10:30作为降交点地方时，星上安装一台CCD相机，卫星具有侧摆能力，视场角为8.6°，焦距2850 mm，选取满月时刻进行对月定标仿真，选取仿真时刻为2018-03-29T10:11:30.000。将3.1节和3.2节中计算结果作为卫星姿态输入参数；采用第一种成像方式时，卫星成像时刻姿态角为[0° 10.51° 174.34°]，补偿俯仰角速度为dθ1=0.546 1(°)/s；采用第二种成像方式时，卫星姿态角为[0° 168.45° 20.18°]，补偿俯仰角速度为dθ2=0.694 5(°)/s。

图15 650 km太阳同步轨道卫星对月定标仿真过程Fig.15 Simulation scenario of satellite lunar calibration in 650km SSO

仿真结果显示：卫星按照上述两种方式对月成像，成像时间分别为t1=0.805 5 s和t2=0.803 8s，与理论计算值的标准推扫时间t=0.804 6s的偏差分别为0.11%和0.10%，可以达到正常成像的理论推扫速度，误差主要来源于月球边缘确定误差和软件本身舍入误差。

4 结束语

对月定标以其高精度、高频次和简单易行的特点，将成为新一代卫星在轨定标的重要方式。为解决对月定标过程中积分时间与推扫速度相失配问题，本文提出了姿态机动补偿方法，在不额外增加仪器、不改变原有扫描行周期的情况下，解决上述问题。针对两种不同的对月成像方式使用姿态机动补偿方法，最后对该补偿方法进行了仿真验证，仿真结果显示：在两种成像方式下，该姿态机动补偿方法都可以实现推扫速度的补偿，使TDICCD相机达到正常对月成像的推扫速度，解决过采样问题，由于该方法具有不改变原有行周期的特性，因此也适用于积分时间固定的普通线阵CCD相机；该方法仅依靠卫星姿态机动实现补偿，比较容易做到，因此可用于各种轨道高度上的光学遥感卫星的对月定标工作，提高定标频次和定标精度。仿真结果中得到的两种成像方式的补偿特点和补偿角速度随时间和星月距离变化的规律，可以用于定标任务总体规划以及定标具体时机的确定，对卫星总体设计和任务规划具有参考意义。

)

[1] 陈福春,陈桂林,王淦泉.卫星遥感仪器的可见光星上定标[J].海洋科学进展，2004，22(z1)：34-38

ChenFuchun，ChenGuilin，WangGanquan.On-orbitvisiblecalibrationforsatelliteremotesensinginstrument[J].AdvancesinMarineScience，2004，22(z1)：34-38 (inChinese)

[2]朱兴鸿,王瑞,白照广.遥感卫星全视场成像质量仿真方法研究[J].航天器工程，2013，22(6)：11-17

ZhuXinghong，WangRui，BaiZhaoguang.Simulationmethodanalysisonfull-viewimagingqualityforremotesensingsatellite[J].SpacecraftEngineering，2013，22(6)：11-17 (inChinese)

[3]樊超,李英才,易红伟.速高比对TDICCD相机的影响分析[J].兵工学报，2007，28(7)：817-821

FanChao，LiYingcai，YiHongwei.Influenceofvelocity-heightratioofsatelliteontheTDICCDcamera[J].ActaArmamentarii，2007，28(7)：817-821 (inChinese)

[4]JiaguWu，ZZHF.RestorationofTDIcameraimageswithmotiondistortionandblur[J].OpticsandLaserTechnology，2010，42(8)：1198-1203

[5]JoeSteyn，GeorgeTyc，KeithBeckett，etal.Rapideyeconstellationrelativeradiometricaccuracymeasurementusinglunarimages[C]//Sensors，Systems，andNext-GenerationSatellitesXIII.Bellingham：SPIE，2009：74740Y1-12

[6]SunJunqiang，XiongXiaoxiong，WilliamLBarnes,etal.MODISreflectivesolarbandson-orbitlunarcalibration[C]//IEEETransactionsonGeoscienceandRemoteSensing.NewYork:IEEE,2007:2383-2393

[7]LLebegue.UsingExoticguidanceforpleiades-hrimagequalitycalibration[C]//The21stISPRS.ChristianHeipke,Germany:ISPRS,2008:13-18

[8]郭强，陈博洋，张勇,等.风云二号卫星在轨辐射定标技术进展[J].气象科技进展,2013(6):6-12

GuoQiang，ChenBoyang，ZhangYong,etal.Progressinon-orbitradiometriccalibrationtechnologyforFengyun-2satellite[J].AdvancesinMeteorologicalScienceandTechnology,2013(6):6-12 (inChinese)

[9]杨秉新.TDICCD在航天遥感器中的应用[J].航天返回与遥感,1997，18(3)：15-18

YangBingxin.ApplicationsofTDICCDinspaceremotesensors[J].SpacecraftRecovery&RemoteSensing，1997，18(3)：15-18 (inChinese)

[10] 任建岳,何斌,王家骐,等.航天光学遥感器像移速度矢计算数学模型[J].光学学报,2004，24(12):1585-1589

Ren Jianyue,He Bin,Wang Jiaqi，et al.Space optical remote sensor image motion velocity vector computational modeling[J].Acta Optica Sinica，2004，24(12):1585-1589 (in Chinese)

[11]马高峰,鲁强,郑勇.JPL行星/月球星历[C]//中国宇航学会深空探测技术专业委员会第一届会议.北京：北京空间飞行器总体设计部,2005:395-401

Ma Gaofeng,Lu Qiang，Zheng Yong.Ephemeris of moon and planet by JPL[C]//The 1stConference for Deep Space Exploration Technology Committee of Chinese Society of Astronautics.Beijing:Beijing Institute of Spacecraft System Engineering,2005:395-401 (in Chinese)

(编辑：李多)

Attitude Maneuver Compensation Method on Lunar Imaging for Optical Remote Sensing Satellite

GAO Han BAI Zhaoguang LU Chunling DI Guodong

(DFH Satellite Co., Ltd.，Beijing 100094，China)

On-orbit lunar calibration takes advantage of not relying on calibration field or weather and is more effective. But attitude control and imaging parameters matching design problem should be solved. An attitude maneuver compensation method is proposed for the optical remote sensing satellite to solve the mismatch of integral time and scanning rate when the TDICCD camera carries out the lunar imaging task. And a sun-synchronous orbit remote sensing satellite is taken as an example for analysis. The satellite’s compensation angular velocity which enables the regular imaging is calculated and verified by the simulation software. The simulation method shows that the method proposed in this article can be used to match integral time and scanning rate and obtain valid lunar images.

TDICCD；lunar imaging；attitude maneuver compensation

2015-11-17；

2016-03-27

高涵，男，硕士研究生，研究方向为航天器总体设计。Email：m18600208173@163.com。

V412.4

A

10.3969/j.issn.1673-8748.2016.04.002