伺服系统机械谐振机理与抑制方法分析
2016-03-16那学智柴晓慧
夏 超,那学智,柴晓慧,宋 涛
(北京自动化控制设备研究所,北京100074)
伺服系统机械谐振机理与抑制方法分析
夏 超,那学智,柴晓慧,宋 涛
(北京自动化控制设备研究所,北京100074)
现今高性能伺服系统对系统带宽提出了越来越高的要求,而传动轴、联轴器、减速器等传动机构均存在一定的弹性,使得系统具有一定频率的谐振点。当系统带宽覆盖该谐振频率时,系统就会发生机械谐振现象。尤其对减速器等必然存在传动间隙的传动装置,间隙的存在极大地降低了传动刚度,并加剧谐振带来的危害。在分析伺服系统机械谐振产生机理的基础上,对目前国内外关于抑制机械谐振的各种方法进行了介绍与分析。针对舵系统应用背景指出了几种具有良好应用前景的抑制方法,并着重进行了分析与研究。
伺服系统;间隙;机械谐振;谐振抑制
0 引言
在伺服系统中,一般需要通过传动机构,如传动轴、联轴器、减速器等来连接伺服电机与负载。而实际的传动机构均会存在一定的弹性,这样就使得系统本身存在一定的谐振频率。随着当今高性能伺服系统带宽的增加,往往会覆盖该谐振频率,而导致系统发生机械谐振。机械谐振会影响系统的控制性能和精度,甚至损害传动装置、烧毁电机。尤其是使用减速器的场合,传动间隙的存在会大大降低传动刚度,使得系统更加容易发生机械谐振,加剧谐振所带来的危害。
一般可以从机械设计和控制率设计两个方面来抑制伺服系统的机械谐振。从机械设计角度抑制机械谐振主要是通过优化机械结构的设计、使用刚度高的材料、改进加工和装配工艺等方法减小传动间隙、提高传动刚度,从而提高谐振频率,使其不与系统带宽发生重叠[1];从控制率设计角度抑制机械谐振又可以分为被动抑制与主动抑制两个方面。被动抑制是通过降低控制增益以减小系统带宽,或使用陷波器/滤波器滤去谐振频率成分等方法,达到避免谐振的目的,均是以在不同程度上牺牲系统的性能为代价的,而且会存在系统适应性差等缺点[2]。
主动抑制是通过改造系统控制结构、使用智能控制算法、构造观测器等方法抑制间隙和弹性的负面影响,以提高系统的控制刚度,避免发生谐振。主动抑制策略是目前国内外学术界研究的热点,也存在一定的缺陷,如控制结构复杂、算法计算量大等[3-10]。
本文先通过建模对伺服系统谐振的产生机理进行介绍与分析,然后对目前国内外应用较广或研究较多的谐振抑制方法,如陷波器滤波法、角加速度反馈法、多回路状态反馈法、轴矩观测器法、扰动观测器法等分别进行介绍,对各自存在的优缺点以及在舵系统上应用的可行性进行了分析,最后指出对于舵系统应用场合,角加速度反馈法、多回路状态反馈法、轴矩观测器法是最有应用前景的谐振抑制方法。
1 伺服系统机械谐振产生机理
1.1 伺服机构的双惯量模型
具有弹性连接的伺服机构可以用如图1所示的双惯量模型来表示。其中K和Cw是传动轴的弹性系数与阻尼系数,当传动轴发生扭转形变时会产生扭矩Tw,称为轴矩;Jm、Cm、Te、θm分别为电机的转动惯量、阻尼系数、电磁转矩和旋转角度;Jl、Cl、Tl、θl分别为负载的转动惯量、阻尼系数、电磁转矩和旋转角度。
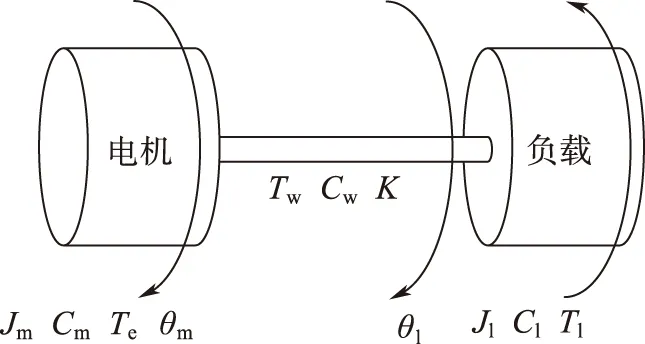
图1 双惯量机械传动模型Fig.1 The model of two-Mass mechanical transmission system
忽略阻尼的影响,可以得到双惯量模型的框图与传递函数,分别如图2与式(1)所示。
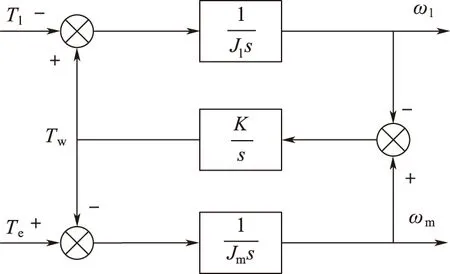
图2 双惯量机械传动模型框图Fig.2 The block diagram of two-Mass mechanical transmission system

(1)
进而可以得出电机转速和负载转速与电机电磁转矩之间的传递函数,分别如式(2)、式(3)所示。
(2)
(3)
从式(2)和式(3)可以看出,双惯量模型存在一对共轭的零极点。零极点的存在使得系统在特点频率下的响应会比较剧烈,从而产生机械谐振现象。
1.2 传动间隙的影响
传动间隙在很大程度上限制了伺服系统的控制性能,产生很多负面的影响,如加剧齿轮磨损、产生速度振荡、降低传动刚度导致系统发生谐振等。目前应用较多的间隙模型是“弹性-死区模型”,如式(4)所示。
(4)
含间隙的双惯量系统的结构如图3所示。
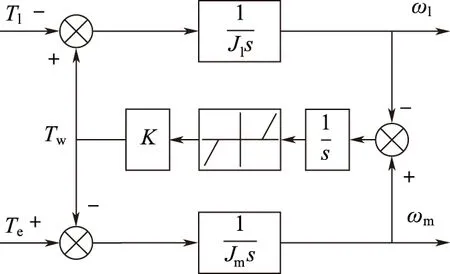
图3 带间隙的双惯量模型框图Fig.3 The block diagram of two-Mass system with backlash
传动间隙会大大降低系统传动刚度,从而降低系统谐振频率,增大谐振幅值,并且还会带来比较严重的非线性影响,加剧谐振危害。
2 机械谐振的抑制方法
2.1 陷波器滤波法
目前大多数商用伺服系统均采用陷波器来抑制机械谐振,如日本的安川、松下公司与德国西门子公司所生产的伺服系统。
从频域分析角度看,机械谐振的根本原因在于系统的幅频特性在某一频率处有较大的幅值,而陷波器能大大降低系统在指定频率处的幅值而不影响其他频率处的特性。所以使用陷波器抑制机械谐振比较简单且有效。
如图4所示,一般将陷波器放在速度控制器之后对电流指令信号进行滤波处理。
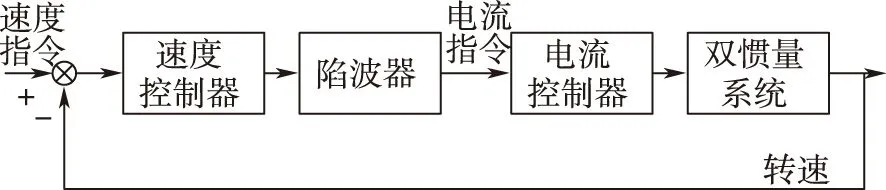
图4 采用陷波器滤波的双惯量系统控制框图Fig.4 The control block diagram of two-Mass system using notch filter
使用陷波器的优势在于简单、成本低廉,但需要事先精确地知道系统谐振频率,所以一般与扫频技术结合使用。需要在系统初始化阶段扫描系统频率特性,根据得到的谐振频率值配置陷波器参数。这也在一定程度上限制了该方法的应用范围。而且由于陷波器存在一定的相角滞后,所以系统中陷波器的数量不能过多,如果系统受干扰或参数变化导致谐振频率发生变化,则陷波器的抑制作用失效,反而会对系统造成不利的影响。而且陷波器对于抑制间隙这种非线性因素所造成的机械谐振效果较差,所以不适合应用于舵系统。
2.2 角加速度反馈法
角加速度反馈已在工程应用中得到广泛的证明,能够有效地抑制系统谐振,并拓宽系统带宽。文献[3]将角加速度反馈应用在机器人动力学解耦控制上面,证明角加速度反馈在抑制扰动、提高跟踪性能方面具有良好的效果。文献[4]与文献[5]利用角加速度反馈抑制系统的谐振,取得了良好的效果,并证实了角加速度反馈是一种有效增加系统带宽的方法。目前,角加速度反馈已经广泛应用于机器人关节控制、谐波驱动机构等场合,在抑制谐振、增加系统带宽和提高系统稳定性方面取得了良好的效果。
角加速度反馈能够抑制系统谐振的机理是引入角加速度反馈能够提高系统的主动阻尼、大幅增加电机的等效转动惯量。图5表示的是一种典型的采用角加速度反馈的双惯量系统控制结构,其中角加速度直接从负载侧得到。
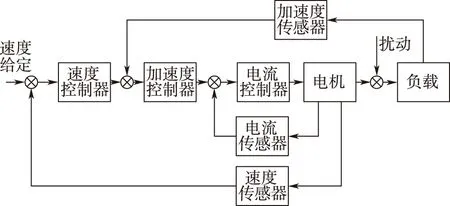
图5 采用角加速度反馈的双惯量系统控制框图Fig.5 The control block diagram of two-Mass system using acceleration feedback
一般在设计带角加速度反馈的控制系统时需要注意如下几个方面:
1)在保证系统稳定的前提下,角加速度控制器的增益要尽可能大;
2)为了避免对外环造成较大的影响,角加速度环的相位损失不能太大;
3)引入角加速度反馈会带来一定的相位滞后,所以外环控制器需要进行一定的相位补偿。
角加速度负反馈可以有效地抑制系统的谐振,但同时也会压缩系统的带宽。角加速度正反馈能拓展系统的带宽,但是又会放大系统的谐振与高频干扰,一般都需要加入低通滤波器使用。所以,通过两个滤波器将两个通道并联以将两种反馈方式在频率上错开的方式,不失为一种综合了各自优点的方法。
将角加速度反馈应用于舵系统的主要困难在于角加速度信号的获取。由于角加速度环的增益较大,通过将码盘、旋变等传感器输出的位置信号进行二次微分的方式,会大大放大系统的测量噪声,所以应用效果不佳。作为内环,角加速度环的带宽应尽可能高,而目前国内的角加速度计带宽普遍偏低。此外,角加速度计的体积、成本、可靠性等因素也是制约其在舵系统中得到应用的重要障碍。但总体来说,角加速度反馈法是一种简单、有效、可靠的谐振抑制方法。
2.3 多回路状态反馈法
目前国内外大多数关于伺服系统机械谐振抑制的研究,都采用基于PI控制与单个状态量反馈控制相结合的方法。文献[6]从零极点配置的角度研究双惯量系统,对目前学术界已提出的各种通过状态反馈,解决双惯量系统谐振问题的方法进行了对比研究。
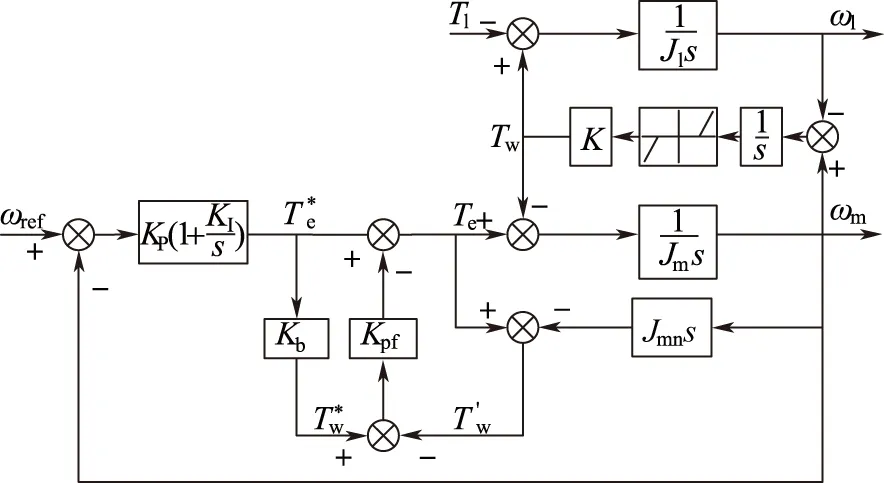
图6表示的是各种应用状态反馈控制的双惯量系统控制框图。目前学术界已提出的各种使用状态反馈抑制双惯量系统谐振的方法大致可以分为三种类型,分别如图6中的A、B、C所示。三类方法所引入的状态反馈各不相同,A型是通过在电流/转矩环里引入转矩/角加速度反馈;B型是通过在电流/转矩环里引入速度反馈;C型则是在速度环里引入转矩、角加速度、速度等各种状态反馈。

图6 各种应用状态反馈的双惯量系统控制框图Fig.6 The control block diagram of two-Mass system using additional feedbacks
文献[6]通过对三种控制结构的理论分析,得出结论:任何一种单路状态反馈都不能从理论上同时配置系统的阻尼系数ζ与无阻尼振荡频率ωn,为了自由配置ζ与ωn,则必须使用两路及以上的状态反馈。
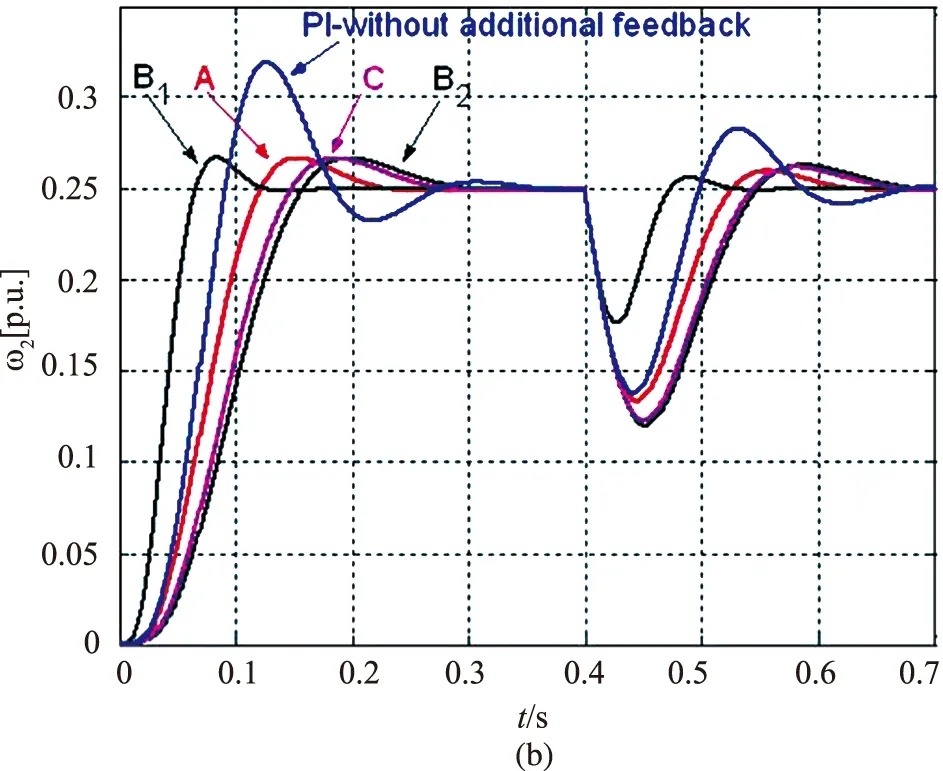
图7表示的是在阻尼比相同时,各种单路状态反馈控制系统的零极点位置和阶跃—加载速度动态响应曲线的示意图。无状态反馈时,纯PI控制器无法对ζ和ωn进行配置。B型反馈在同阻尼系数ζ时对应两个振荡频率ωn,分别对应B1、B2。从图中可以看出,在同阻尼比时各种状态反馈控制系统的无阻尼振荡频率大小顺序为:B1>A>C>B2,由于系统上升时间与ωn成负相关的关系,所以各系统上升时间的大小顺序为B1 图7 同阻尼比时各状态反馈控制系统的(a)闭环零极点位置与(b)阶跃—加载速度动态响应曲线Fig.7 (a)Close-loop pole location and (b)load-speed transient of all considered systems with the same damping coefficient 从第1节的内容可知,带双惯量环节的闭环伺服系统实际上是一个四阶系统,所以纯PI控制器以其仅有的两个控制参数完全无法对系统的零极点进行自由配置,单路状态反馈则可以对ζ和ωn之一进行配置,但若要对ζ和ωn均进行自由配置,则至少需要两路状态反馈。 对于双惯量系统来说,多回路状态反馈控制是一种理论上非常完美的控制策略,可以从原理上自由配置系统的各项参数,可以自由调节系统的调整时间与超调量等。但是对于舵系统等实际工程应用而言,则存在一些困难。比如电机的转速与负载速度一般是通过位置信号微分得到的,如再对其进行微分则会放大系统噪声,精度也会受到影响。而对于其他状态量如轴矩Tw,则缺乏有效的检测手段。另外多回路状态反馈控制算法的计算量,对于舵系统而言也是需要考虑的因素。 2.4 轴矩观测器法 轴矩扰动观测器是一种基于对轴矩的辨识值来对电机的电磁转矩进行补偿的方法。补偿的理想效果是,重新将双惯量系统视作单惯量系统进行控制,即将双惯量系统的弹性与间隙的影响全部补偿掉了。使用轴矩观测器的双惯量系统控制框如图8所示。 图8 应用轴矩观测器的双惯量系统控制框图Fig.8 The control block diagram of two-Mass system using shaft torque compensator ωm=ωl (5) 补偿系数Kpf的选择对系统的补偿效果也具有较大的影响。图9表示的是在不同补偿系数Kpf时系统的开环根轨迹示意图。从图中可以看出,在Kpf<1时,随着Kpf的增大,系统极点逐渐向系统零点靠近;当Kpf>1时,系统进入发散状态;当Kpf=1时,系统等效为单惯量系统,但此时系统为临界稳定状态。 图9 不同补偿系数Kpf时系统的根轨迹示意图Fig.9 The scheme of the system’s root locus at different Kpf 文献[7]提出了一种选取最优Kpf值的方法。首先,定义两个参数:E和F,如式(6)所示。 (6) E表征电机与负载转速的同步程度,即能表征系统传动刚度的大小;F表征的是电机转速受负载转矩影响的大小。由于电机转速参与速度环控制,所以F能够间接地表征系统的抗干扰能力。 文献[7]试图通过研究不同的Kpf值对E和F的影响,找出Kpf的最佳取值。研究结果表明,F几乎不随着Kpf值的改变而发生大的变化;但是E却与之相反,其频率特性的谐振峰值会随着Kpf值的改变而发生较大改变。所以最终使得E频率特性谐振峰值最小的值就是Kpf的最佳取值。 轴矩观测器法简单有效,不依赖负载与间隙等参数值,不需要检测多个系统状态量,仅需对电机转速进行检测,而且使用的电机转动惯量参数也容易获得。所以使用轴矩观测器法抑制系统谐振对于舵系统应用而言具有较好的实用意义。 2.5 扰动观测器法 关于系统模型参数的摄动、外部扰动等的鲁棒性设计研究一直是学术界关于谐振抑制研究领域的热点。而应用扰动观测器是一种有效的策略,所以目前学术界关于应用扰动观测器抑制伺服系统机械谐振的研究较多。应用扰动观测器抑制机械谐振的机理是,将间隙等非线性因素视作为系统受到的扰动,通过对扰动进行观测和补偿,从而抑制间隙的影响。图10表示的是应用扰动观测器以抑制系统扰动的控制系统结构示意图。 图10 应用扰动观测器的控制系统结构示意图Fig.10 The scheme of the control system using disturbance observer 文献[8]将扰动观测器应用在仿生机器人的关节控制上,指出扰动观测器中滤波器Q的设计对于系统的控制效果非常关键。文献[9]针对双惯量系统,对滤波器Q的设计进行了深入的研究,并对扰动观测器的降阶以及离散化等,均进行了详细的分析与研究。文献[10]同样对使用扰动观测器抑制双惯量系统机械谐振进行了深入的研究,并提出了低通滤波器设计的两条应遵循原则,进而对扰动观测器的灵敏性与鲁棒性进行了仔细分析。 扰动观测器的优点就是,其整定参数与原系统参数无关,所以在高精度运动控制领域得到了广泛的应用。对于舵系统这类高阶系统而言,扰动观测器的设计比较复杂,工程设计难度较大。而且如果系统参数变化较大时,扰动观测器的观测准确度也会下降,从而影响控制性能。值得关注的是,最近小数阶的扰动观测器成了一个研究热点,其突出优点是,可以在最大范围内兼顾系统鲁棒性和谐振的抑制能力。但由于其本质是高阶控制器,所以其面临的首要问题也是如何在工程上得到实际应用。 本文对伺服系统机械谐振的抑制方法进行了研究。首先使用双惯量模型以及间隙的死区模型对伺服系统的机械谐振机理进行了分析。然后从目前学术界提出的各种机械谐振抑制方法中选取了五种具有代表性和实用意义的抑制方法进行了介绍与分析,并以舵系统应用为背景,对各种方法的优缺点分别进行了分析。经过对比分析可以看出,对于舵系统应用而言,角加速度反馈法、多回路状态反馈法和轴矩观测器法是最有应用前景的谐振抑制方法。 [1] Brett R Murphy,Ichiro Wdtanable.Digital shaping filters for reducing machine vibration[C].IEEE Trans.Robot.And Auto.,1992,8(2):289-289. [2] P.Schmidt,T Rehm.Notch filter tuning for resonant frequency reduction in dual Inertia systems[C].IAS Annual meeting(IEEE Industry Applications Society),1999,3:1730-1734. [3] Xu W L,Han J D,Tso S K,et al.Contact transition control via joint acceleration feedback[C].IEEE Transactions on Industrial Electronics,2000,47(1):150-158. [4] Tang Tao,Huang Yongmei,Zhang Tong,et al.Reduction of mechanical resonance based on load acceleration feedback for servo system[J].Opto-Electronic Engineering,2007,34(7):14-17. [5] George Ellis,Lorenz R D.Resonant load control methods for industrial servo drives[C].IEEE Industry Applications Society Annual Meeting,2000,3:1483-1455. [6] K Szabat,T Orlowska-Kowalska.Vibration suppression in a two-mass drive system using PI speed controller and additional feedbacks—Comparative study[C].IEEE Trans.Ind.Electron.,2007,54(2):1193-1206. [7] M Odai,Y Hori.Speed control of 2-inertial system with gear backlash using gear torque compensator[C].IEEE AMC. COIMBRA,1998:234-239. [8] B J Jung,J S Kong,B H Lee,et al.Backlash compensation for a humanoid robot using disturbance observer[C].IEEE Industrial and Electronics Society,2004:2142-2147. [9] C S Kim,M J Kang,J H Kim,et al.Implementation ofdisturbance observer for compensation backlash[C].ICROS-SICE International Joint Conference,2009:1812-1816. [10] I Kolnik,G Agranovich.Backlash compensation for motion system with elastic transmission[C].IEEE Convention of Electrical and Electronics Engineer,2012:1-5. Analysis on Mechanism and Suppression of Mechanical Resonance in Servo System XIA Chao,NA Xue-zhi,CHAI Xiao-hui,SONG Tao (Beijing Institute of Automatic Control Equipment,Beijing 100074,China) Nowadays,the need for even higher bandwidth is arising for high-performance servo systems.But the mechanical resonance occurres if the bandwidth of servo system covers the resonance frequency which is existing due to the elasticity of transmission mechanism,such as shaft,coupler and reducer,especially for those with transmission clearance in,like reducer.The existence of transmission clearance can largely reduce the rigidity of transmission and intensifies the effect of resonance.In this paper,the causes of mechanical resonance,the advantages and disadvantages of some suppression methods proposed by researchers are discussed.And the ones that have good applicability in electro-mechanical actuation system are analyzed in detail. Servo system;Backlash;Mechanical resonance;Suppression of mechanical resonance 2015-03-18; 2015-06-15。 夏超(1991-),男,硕士,助理工程师,主要从事电动伺服系统方面的研究。E-mail:xiachao_hit@163.com TN820.3 A 2095-8110(2016)01-0029-07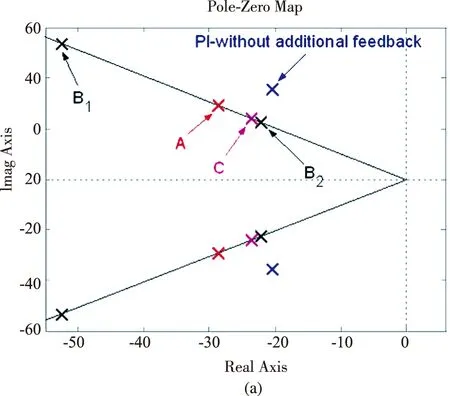




3 结论
