基于DDPG的柔性伺服系统级联陷波器设计

钟靖龙，宋 宝,，刘永兴，徐必业

(1.华中科技大学 机械科学与工程学院，武汉 430074;2.广东拓斯达科技股份有限公司，广东 东莞 523822)

0 引 言

在交流伺服系统中，伺服电机一般采用联轴器、同步带、丝杠(传动轴)等驱动负载，使得伺服系统具有柔性特征，从而导致伺服系统运动时容易产生机械谐振。当系统处于谐振状态时，电机电流及转速发生震荡，不仅会产生噪声，严重的还会对机械传动部件以及电机造成损坏，甚至出现断轴等后果[1]。常用的振动抑制方法有低通滤波器、陷波器以及加速度反馈等[2-4]。其中，陷波器由于结构简单、控制回路增益高等优势而得到广泛应用。

然而当陷波器参数选择不恰当时，不仅无法对谐振形成有效的抑制，甚至会导致更激烈的振动，影响正常使用。针对陷波器参数中最重要的陷波中心频率，Yazdanian[5]等人提出一种基于扩展卡尔曼滤波的谐振频率估计方法；另外，基于FFT的谐振频率快速获取方法也在诸多工业伺服系统中得到了验证应用[6-7]。同时，针对陷波器其他参数的整定，Tim等人[8]通过研究陷波深度与零点阻尼比的对应关系在线整定深度参数，而Park等人[9]提出一种利用随机衰减法与峰值检测法的陷波器深度参数实时整定方法，并在滚珠丝杠驱动和皮带驱动两种负载的伺服系统上进行了实验验证。然而，上述方法大多数仅针对单陷波器中陷波频率以及陷波深度进行整定，而没有涉及到陷波宽度以及级联陷波器的参数整定问题。

本文提出一种基于DDPG的级联陷波器参数整定方法。在分析系统传动函数的基础上，通过扫频得到系统速度环开环bode图，结合陷波器bode图，将二者统一化预处理结果作为DDPG输入数据，并以相位裕度为奖励函数，利用陷波器参数偏移量与预处理数据计算奖励函数来训练神经网络，得到级联陷波器的深度及宽度优化参数。并采用驱动/负载电机、柔性轴、惯量盘、联轴器等搭建了三质量柔性伺服系统实验平台，采用ARM+DSP 进行算法集成，并开展实验验证，结果表明该方法可以对级联陷波器参数进行有效整定并抑制系统谐振。

1 柔性伺服系统建模及谐振分析

为了更好的表征伺服传动机构柔性连接特征，在此将由伺服电机、纯惯性负载以及等效传递轴三者柔性伺服系统等效为三质量系统。

图1为三质量系统模型。

图1 三质量系统模型

电机与执行器之间通过刚度分别为Ks1和Ks2，阻尼系数分别为Cw1和Cw2的柔性连接器以及一个惯量为JTr的传递轴连接，系统的动力学方程为

(1)

图2为三质量系统的控制框图。

图2 三质量系统控制框图

Tm与ωm之间的传递函数为

(2)

式中，ωNTFi、ωANFi分别为三质量系统的谐振频率与反谐振频率，可通过式(3)计算得到

(3)

2 级联陷波器及谐振特征辨识

2.1 级联陷波器

为了有效抑制系统多频谐振，设计串联多个单陷波器组成级联陷波器，对实际伺服传动系统中多频率谐振进行有效抑制，式(4)给出了级联陷波器的传递函数。

(4)

式中，Hi(s)为第i个陷波器的传递函数，为保证其参数互相独立以便于单独调整，本文采用如式(5)所示的三参数陷波器。

(5)

式中，ωn为陷波滤波器中心频率，宽度参数ξwidth为-3 dB频带宽度与中心频率的比值，深度参数kdepth陷波中心深度，幅值衰减为20lgkdepthdB。当陷波中心频率为450 Hz时， 参数ξwidth和kdepth对陷波滤波器性能的影响如图3所示。其中，图3(a)为kdepth=0.1时，不同宽度参数ξwidth下的bode图；图3(b)为ξwidth=0.3时，不同深度参数kdepth下的bode图。

图3 ωn=450 Hz,不同ξwidth、kdepth下的陷波器bode图

2.2 谐振特征辨识

在柔性伺服系统传动过程中，可以通过伺服系统转速或者转矩特性分析出系统谐振的幅值和频率。在矢量控制模式下，Tm∝iq，且电流环较速度环实时性更高，因此本文以伺服系统交轴电流频谱特征，在线辨识系统的谐振特征。图4为机械谐振抑制结构框图。

图4 机械谐振抑制结构框图

在伺服系统中，交轴电流采样结果为有限长非周期序列iq[n]，其离散傅里叶变换形式为

(6)

采用基于频率抽取的FFT可以将N(N=2M)点DFT经过M次分解全部分解为2点DFT，时间复杂度由O(n2)降低为O(N·logN)。

对FFT计算结果进行求平方根计算可得到各频率点对应的幅值，超过既定阈值的幅值所对应的频率即为谐振频率，记录并输出的谐振频率及幅值分别为

(7)

式中，k为幅值超过既定阈值的对应位置，fs为采样频率，N为FFT计算点数，mag为频率点幅值。

3 基于DDPG的陷波器参数整定

为了克服不同工况下电机型号、负载参数及传动设备等差异导致的控制参数难以调整、不通用等问题，提出一种基于DDPG的多参数整定方法，以向量稳定裕度为基础定义奖励函数，并构造深度强化学习算法用于级联陷波器参数整定。

3.1 奖励函数

采用相位裕度为奖励函数，解决陷波器带来的相位滞后问题，增强系统稳定性，提高系统响应。

为了实现系统全局持续稳定，设置其相位裕度保持PM>45°。对于如式(5)所示的陷波器，令s=jω，可得剪切频率ωc处的相位为

(8)

当在系统中加入级联陷波器后，系统的新的相位裕度为

(9)

则奖励函数可定义为

r=PM

(10)

3.2 DDPG算法

在DDPG实现流程中，分别采用卷积神经网络近似策略函数μ和Q函数，即actor网络和critic网络，并分别为之各创建两个神经网络拷贝：online和target。其算法框架如图5所示。

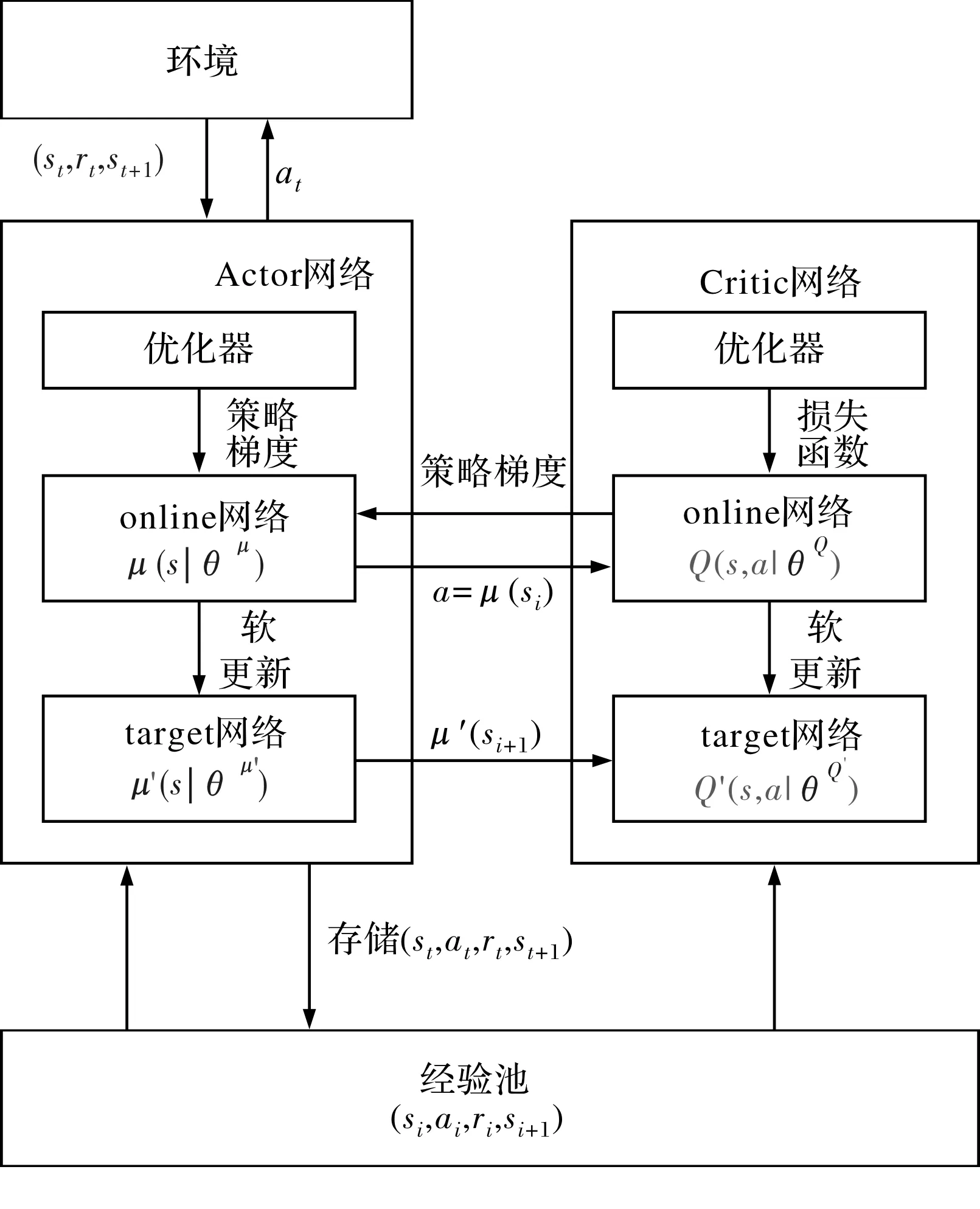
图5 DDPG算法框架

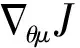
(11)

(12)

而对于critic网络的online网络，通过最小化式所定义的损失函数L进行更新。

(13)

式中，si为当前状态，ai为当前动作，ri为当前奖励函数，N为小批量数据大小，为损失函数。

随机设置一组滤波器参数，以最大相位裕度为训练目标，actor网络输出陷波器参数偏移量，并将其作为下一状态输入到critic网络，直到每一轮训练达到特定的偏移量且每一轮训练的偏移量相同为止，并将具有最大相位裕度的参数存入经验池。

3.3 神经网络结构及参数设计

以双陷波器组成的级联陷波器设计为例，考虑到陷波中心频率的重要性以及可通过FFT精确辨识，故共需要训练4个参数。DDPG算法使用两种神经网络结构——actor网络和critic网络，分别如图 6及图 7所示。其中，actor网络输入为4个当前陷波器参数(kdepth,1&2、ξwidth,1&2)和4个上阶段陷波器参数偏移量，并拥有两个分别具有300和200个单位的隐藏层；输出为4个当前陷波器参数偏移量。该网络除最终输出层采用超正切激活函数外，其余采用矫正的非线性函数。

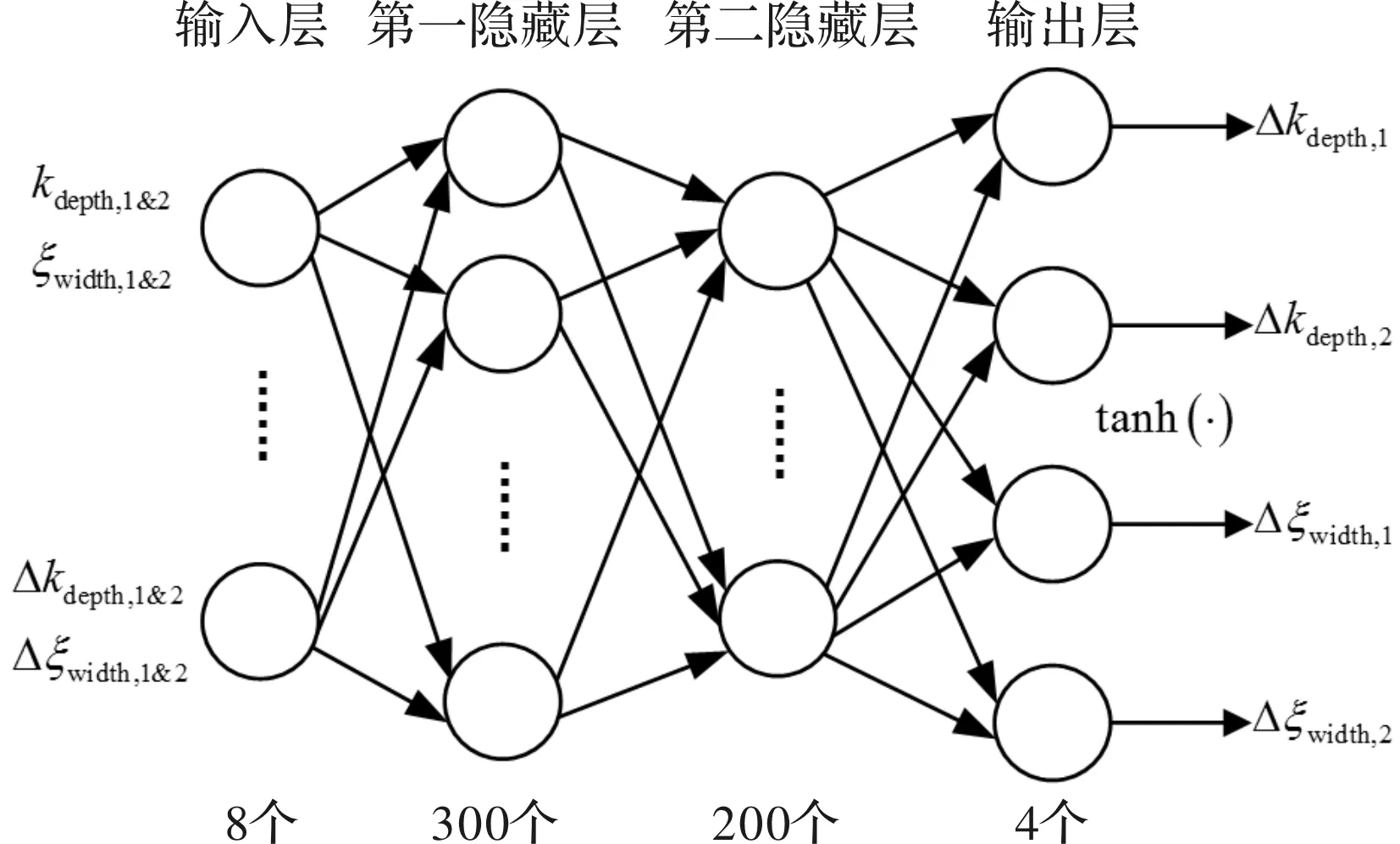
图6 actor网络结构

图7 critic网络结构

critic网络与actor网络大小相同，只是动作被包含在第二层隐藏层之后，输出大小为1。重放缓存区大小为100,000，小批量数据大小为32，最大训练轮数以及每一轮训练步长分别为2,500和100。贴现因子(discount factor)为0.95，动作通过ε从1.0到0.0线性变化的ε贪心策略选取。actor网络及critic网络的学习率分别为0.001和0.002。深度参数kdepth及宽度参数ξwidth选取范围分别为[0.001,1]及[0.0,1.0]。

4 实验及分析

为验证DDPG算法的参数整定能力以及级联陷波器的谐振抑制能力，采用交流伺服电机、联轴器、惯量盘及柔性轴负载搭建了如图8所示实验平台。其中电机参数如表1所示。在实验室自研的基于ARM+FPGA交流伺服驱动器上，采样电机交轴电流，并利用FPGA实现快速傅里叶变换，并基于Pytorch完成对DDPG算法的实现和训练。

图8 级联陷波器实验验证平台

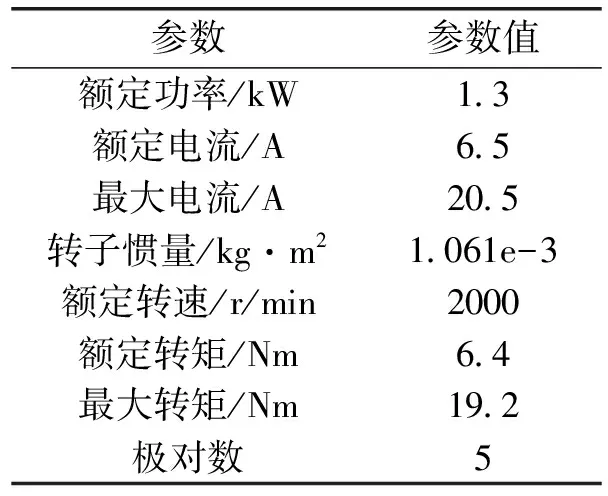
表1 华大电机参数

图9 系统开环bode图

图9为系统速度环开环bode图。图10、图11为应用DDPG对级联陷波器参数的训练过程，训练结果如表2所示。

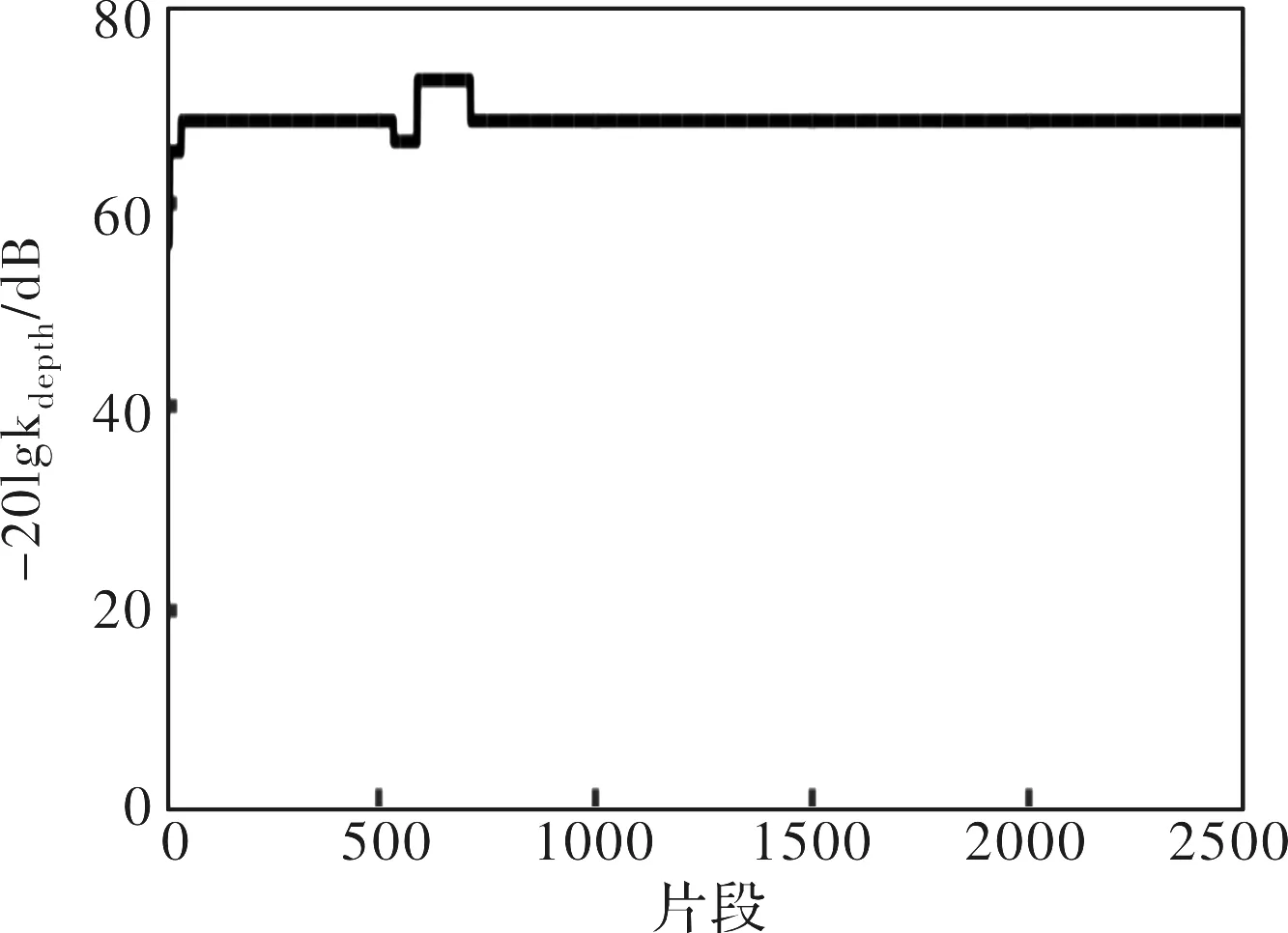
图10 1号陷波器参数整定过程

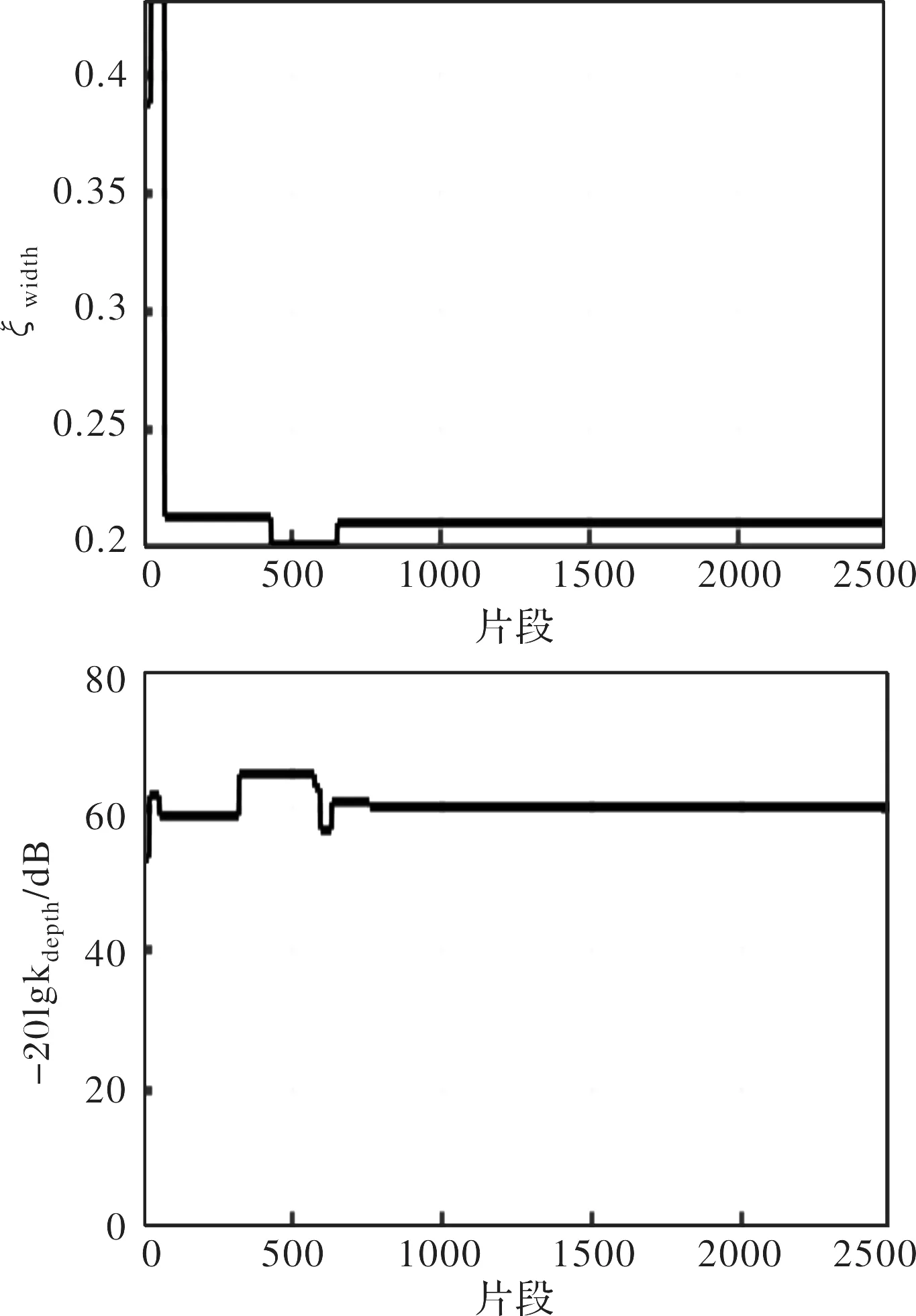
图11 2号陷波器参数整定过程

表2 陷波器参数训练结果

图12 陷波前后速度-电流对比

利用上述参数设计级联陷波器并应用于伺服系统。图12为加入陷波器前后电机反馈速度及交轴反馈电流对比，数值对比如表3所示。

表3 谐振抑制前后性能指标对比

由反馈速度及反馈电流对比可知，基于DDPG算法进行级联陷波器的参数整定，并应用于实际伺服系统，在抑制系统谐振的同时保证了系统的稳定。

5 结 论

针对伺服系统中由于柔性传动部件而导致的多频谐振问题，本文在基于三质量系统谐振机理分析的基础上，提出一种基于DDPG算法的级联陷波器参数整定方法，在保证系统具有最大相位裕度的前提下，成功抑制伺服系统的机械谐振，同时本文提出的方法也可用于其他类型的级联滤波器设计。