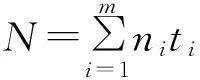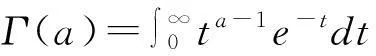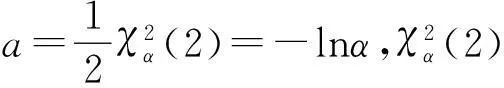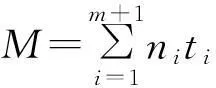基于零失效数据的指数分布可靠性综合评估*

于　录　曲宝忠

(92941部队　葫芦岛　125000)



基于零失效数据的指数分布可靠性综合评估*

于录曲宝忠

(92941部队葫芦岛125000)

摘要武备可靠性试验鉴定中,有时会出现零失效数据的情形,直接应用零失效数据检验、评估指数产品可靠性,可能会造成评估结果“冒进”。针对这个现象,提出引进失效信息,综合加权处理,评定产品的可靠性。并通过实例,验证了引进失效信息综合加权评定零失效数据的指数型产品可靠性,评定结果客观、科学,易于被双方共同接受。

关键词零失效; 指数分布; 可靠性; 失效信息; 评估

Comprehensive Estimation for Reliability of Exponential Distribution Based on the Zero-failure Data

YU LuQU Baozhong

(No. 92941 Troops of PLA, Huludao125000)

AbstractIn the course of reliability test and evaluation of the armament, sometimes the zero-failure data arises. When firsthand the zero-failure data are firsthand applied to inspect and evaluate the product reliability of exponential distribution, perhaps a rash advance result is come into being. Contraposing this proplem, failure information, weight and process the test data synthetially are introduced to evaluate the product reliability. Examples illustrate that the evaluation result of product reliability of the exponential distribution is objective, scientific and accepted by both sides.

Key Wordszero-failure, exponential distribution, reliability, failure information, estimation

Class NumberTP202

1引言

可靠性[1]作为武器装备的重要战技指标是武备试验与鉴定必须考核的指标之一。由于各种条件的限制,在指数分布武器装备可靠性试验中,常采用定时截尾试验方法[2],也就是根据武器装备研制任务书中的指标,作出定时截尾试验检验方案。随着科学技术的进步,武器装备的可靠性越来越高,按照常用的故障数不低于1的试验方案,往往需要很高的试验周期和试验经费。因此,在实际的可靠性鉴定试验中,综合考虑试验周期和试验经费,有时会制定故障数为零的试验方案,即零失效定时试验方案[3]。这就难免在可靠性试验截尾时间到时,经常会出现零失效数据[4],也就是零故障情形。在这种情况下,目前都是根据检验方案,对产品作出接受的决定。其实这样做有一个问题:就是在外推时间处也就是截尾时间的下一时间点处是否会有失效样品出现还不确定。如果此时有失效样品出现,那么对该产品可靠性的评定就可能会产生“冒进”现象。为改善这种“冒进”,可以考虑引进失效信息,进行综合处理,在作出可靠性检验的同时,对产品的可靠性作出估计[5]。

本文主要是针对零失效数据的指数分布产品,引进失效信息,综合加权评估产品的可靠性,以改善由于试验截尾时间“短”,而可能造成评定结果的“冒进”。

2定时截尾试验方法

原假设为H0:θ=θ0,备择假设为H1:θ1=λθ0(λ<1)。其中:θ0为指标的目标值;θ1为指标的最低可接收值;λ为检出比。

设试验时间为T,故障数为Z。决策不等式为

(1)

当不等式(1)成立时,拒绝H0,否则采纳H0。

接收原假设H0的概率:

(2)

式中:π0为验前概率,T0为验前试验时间,Z0为故障数。

拒绝原假设H0的概率:

π1=1-π0

(3)

判决数:

(4)

生产方风险:

(5)

使用方风险:

(6)

3可靠性估计

假设对某武备进行m次定时截尾试验,在第i(i=1,2,…,m)次定时截尾试验中,截尾时间为ti(t1

3.1零失效数据可靠性估计

指数分布产品的分布函数[6]可表示为

F(t)=1-e-λt,t>0,λ>0

(7)

式中:λ为失效率[7],是需要评估的特征参数。

λ的密度函数为

f(t)=λe-λt

(8)

若λ的先验密度函数的核为λa-1,则λ的先验密度函数为

π(λ)∝λa-1

(9)

式中:0

针对指数分布产品m次定时截尾试验的零失效数据{(ti,ni),i=1,2,…,m},若λ的先验密度函数由式(9)给出,在零失效数据情形下,λ的似然函数[8]为

L(0|λ)=e-Nλ

根据Bayes定理,则λ的后验密度函数为

(10)

在平方损失[9]的情况下,失效率λ的Bayes估计为

(11)

可靠性θ的Bayes估计为

(12)

3.2引进失效信息后可靠性估计

现在获得m次定时截尾试验的零失效数据为{(ti,ni),i=1,2,…,m},若在m+1次定时截尾试验中,截尾时间为tm+1,相应的试验样品数为nm+1,结果有r(r=0,1,…,nm+1)样品失效。由于实际上m+1次定时截尾试验并没有进行,也不允许进行。因此tm+1、nm+1和r均是未知的。

现取tm+1为tm再加上前m次定时截尾试验的平均试验间隔时间,即

(13)

取nm+1是前m次定时截尾试验的平均样品数(取整),即

(14)

其中,[x]表示不超过x的最大整数。

现假如在m+1次定时截尾试验中,截尾时间为tm+1,相应的试验样品数为nm+1,结果有1个样品失效。若λ的先验密度函数仍由式(9)给出,在1个样品失效情形下,λ的似然函数[4]为

L(1|λ)=nm+1tm+1λe-Mλ

根据Bayes定理,则λ的后验密度函数为

(15)

在平方损失的情况下,失效率λ的Bayes估计为

(16)

式中:a的取值同式(14)。

可靠性θ的Bayes估计为

(17)

3.3可靠性的加权综合估计

(18)

可靠性θ的加权综合估计为

(19)

4实例分析

某型导弹的自动化测试设备可靠性试验数据如表1所示。共有七组数据,试验时间单位:小时。

4.1实例计算

根据式(11)、式(12)得到零失效数据可靠性估计;根据式(13)、式(14)、式(16)和式(17)得到引进失效信息后可靠性估计;根据式(19)得到可靠性的加权综合估计。具体结果如表2所示。

表1　某自动化测试设备截尾试验数据

表2　失效率及可靠性估计结果

4.2结果分析

1) 从计算结果可以看出,在定时截尾试验中,若直接应用零失效数据对装备的可靠性进行估计,因为无法预知截止时间的下一时间点是否会有失效样品出现,而造成评估结果较为冒进。

2) 若在零失效数据中,直接引进1个失效样品评估装备的可靠性,由于引进了1个失效数据,就相当于肯定截止时间的下一时间点会出现1个失效样品,缺乏事实依据,所以使评估结果过于保守。

3) 在零失效数据中,引进1个失效样品,进行综合处理加权后,得到的评估结果既避免了零失效数据评估的冒进,又避免了直接引进1个失效样品进行评估的保守,符合产品可靠性具有连续性特点,而且使评估结果易于被双方接受。

5结语

在指数分布产品可靠性评定试验中,针对试验数据零失效情形,引进1个失效样品,进行加权处理,综合评定产品的可靠性,既避免了评估结果的冒进,又使评估结果客观、科学,易于被双方共同接受。

参 考 文 献

[1] 曾天翔,等.可靠性维修性保障性术语集[M].北京:国防工业出版社,2002:33.

[2] 任占勇,等.GJB 899A-2009[S].北京:中国人民解放军总装备部,2009:24-29.

[3] 李金国,等.高可靠性航空产品试验技术[M].北京:国防工业出版社,2011:201-204.

[4] 韩明.基于无失效数据的可靠性参数估计[M].北京:中国统计出版社,2005:1-2,107-109.

[5] 曲宝忠,等.海军战术导弹试验与鉴定[M].北京:国防工业出版社,2005:123-124.

[6] 李湘宁.基于ML-Ⅱ的指数分布可靠性多层Bayes估计[J].现代防御技术,2012(4):81-82.

[7] 周正伐,等.航天可靠性工程[M].北京:宇航出版社,2007:193-196.

[8] 韩明.可靠性参数的修正Bayes估计法及其应用[M].上海:同济大学出版社,2010:11-13.

[9] 茆诗松,王静龙,等.高等数理统计[M].北京:高等教育出版社,2002:167-169.

[10] 韩明,等.失效率的综合-Bayes估计[J].数学物理学报,2005,25:678-680.

中图分类号TP202

DOI:10.3969/j.issn.1672-9730.2016.02.028

作者简介:于录,女,硕士,研究方向:导弹武器系统试验与鉴定。曲宝忠,男,硕士,研究方向:导弹武器系统试验与鉴定。

*收稿日期:2015年8月10日,修回日期:2015年9月18日