初中数学中的分类讨论

戴灿阳

（南安市康美中学，福建南安362332）

初中数学中的分类讨论

戴灿阳

（南安市康美中学，福建南安362332）

文章指出在初中数学教学阶段常遇到的数学思想方法，特别就分类讨论提出了根据“概念”“字母的取值范围”“几何图形的特征”“结论的几种可能”的分类类型，重点在于对分类讨论的归纳总结。

分类讨论；思想方法；初中数学教学

初中数学的题型变幻莫测，不变的是数学思想方法，数学思想在教学中有着广泛的应用，初中数学课程标准指出，数学思想在义务教育阶段应结合教学内容进行逐步渗透，在教学中要尽量使学生在解题过程中自己悟出其中的数学思想方法。教师需因势利导，结合学生的生活实际进行全面分析，让学生进一步理解并运用所涉及的数学思维方式去处理，这对加深学生对基础知识的理解，学会在错综复杂的题海中形成初步建模从而解决问题的能力有着深远的影响。

初中数学学习中学生常遇到的的数学思想方法有三类：一般数学方法：配方法、待定系数法、判别式法、换元法、割补法等；数学思维方法：分析法、综合法、反证法、归纳法等；数学思想：分类讨论思想，数形结思想、化归思想、函数与方程思想等。数学思想是其最本质的内容。当研究的对象不能用统一的方法进行研究时，就需要对研究对象进行分类，其实质是寻找对象的异同点，将问题按一定的标准划分为若干不同的类别，并力求分类全面性与代表性，这就是分类讨论思想。教学中通过分类讨论思想的渗透,可以引导学生把复杂问题化为简单问题,提高其有学习数学过程中解决问题的能力。在教学中对这一点应该有充分认识并积极引导，让学生能够灵活运用。

作为数学的重要思想之一，分类思想划分的规则是：第一，划分后各个子项应当互不相容（不重）；第二，划分后各个子项必须穷尽母项（不漏）；第三，每次划分都应按同一标准。学生在初中阶段可能引起分类的题型主要有：（1）概念或字母的不同取值范围分类；（2）题目条件和范围的限制分类;（3）图形的位置或形状分类；（4）题目条件和结论分类。

解答需分类讨论的题型的关键是培养分类讨论的意识，尽量让思考更加全面，注意分类可能导致问题发生质的变化的各种情况。要让学生体会到只有通过分类讨论后所得到结论的完整性与准确性。

一、根据概念进行分类

正数集合：(……)；整数集合：(……)

负数集合：(……)；负分数集合：(……)

分析：本题主要考查有理数的有关概念与分类，可根据整数、分数、正数、负数的定义直接判断。（1）有限小数或无限循环小数都可转化为分数，故这样的小数也叫分数，填分数集时不要漏掉；（2）0虽然既不是正数也不是负数，但它是整数。

解析：本题是对定义的分类，学生要掌握有理数及其相关概念的分类，才能正确分类。

二、根据字母的取值范围进行分类

例2.若|a|=3，|b|=2，且a>b，则a+b=（）.

分析：在进行二次根式的化简与计算时，要注意题目中所给的条件，往往要先化成绝对值，再根据绝对值符号里的式子的性质去掉绝对值符号。在本题中，a的取值情况没有说明，就要注意题目中的隐含条件，根据情况考虑用分类讨论进行求解：

原式转化为|a-5|+|2-a|，再分成三种情况进行讨论：

（1）a≥5，

（2）a≤2，

（3）2＜a＜5，

初中数学最先遇到的分类思想就是数的分类、绝对值的意义、不等式的性质等，学生掌握好了对今后这类题型的理解渗透都会有积极的作用。

三、根据几何图形的特征进行分类

例4.等腰三角形的一边长为3cm，周长是13cm，那么这个等腰三角形的腰长是（）.

A.5cmB.3cmC.5cm或3cmD.不确定

分析：本题中所给的条件是一边长3cm，就有两种可能：3cm作底或作腰。就需要用分类讨论。

解析：（1）当3cm作底时，腰长为（13-3）÷2=5cm。

（2）以3cm作腰时，底边长为13-2×3=7cm，但7>3+ 3，因此这种情况不存在，舍去。故腰长只有5cm，选A。

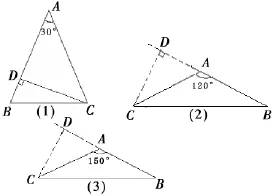
例5.已知等腰三角形一条腰上的高等于该三角形某一边长度的一半，求其顶角.

分析：题目的已知条件中，只告诉我们高是三角形某一边长的一半，那么它既可能是腰长的一半，也有可能是底长的一半，高可能在三角形外部，也有可能在三角形内部，因此，必须根据已知条件逐一进行分类讨论。

解析：在等腰△ABC中，AB=AC，有三种可能：

（1）这条腰上的高等于腰长的一半

①如图（1）

②这条腰上的高等于腰长的一半如图（3）

⑵这条腰上的高等于底长的一半如图（2）

A.5或-1B.-5或1;

C.5或1D.-5或-1

分析：本题考查绝对值的定义，对绝对值的理解是初一数学的一个难点，注意从数形结合入手，其本质就是数轴上两点之间的距离，所以|a|可以看成表示a与表示0（即原点）之间的距离。当|a|=3时，因为无法确定a>0或a＜0，所以a有两种可能3或-3，同样b也有两种可能，由于a>b，所以本题需要进行分类讨论再确定a+b的值。

解析：由|a|=3，|b|=2可得a=3或-3，b=2或-2，

又a>b，则有两种可能：

（1）若a=3b=2；

（2）若a=3b=-2。

四、根据结论的几种可能进行分类

例6.如图，直线AB分别与两坐标轴交于点A（4，0）、B（0，8），点C的坐标为（2，0）。在线段AB上有一动点P，连结CP，是否存在点P，使△ACP与△AOB相似，若存在，求出点P的坐标，若不存在，请说明理由。

分析：△ACP与△AOB有一公共角∠BAO，并且△AOB是一个直角三角形，所以当△ACP除了∠CAP外，只要再有一个角为直角，则两个三角形就会相似，而这个角可以是∠ACP，也可以是∠APC.,因此本题要用分类讨论的方法进行求解。进行分类讨论，全面解决问题，严防漏解。若要使△PCQ与△ACB相似，存在，分两种情况：

解析：第一种，如图：当∠ACP=90°时，CP∥OB易得△ACP∽△AOB

第二种，如图：CP⊥AB，由∠APC=∠AOB=90°，∠PAC=∠BAO得△APC∽△AOB

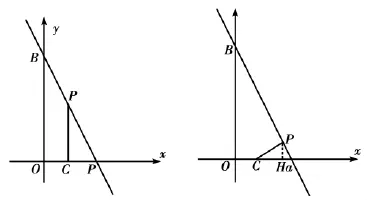
以上对初中数学中出现的分类讨论的几种常见的题型进行了分析，这些题目学生经常接触，教学时要让学生领会分类讨论的方法和重要性，学生在学习应用中逐渐体会感知该种数学方法，在运用分类的思想进行解题时，可以按如下步骤进行处理：（1）判断是否要分类讨论；（2）确定分类对象；（3）确定分类标准进合理分类，做到不重不漏；（4）逐类讨论；（5）得出结论。初中数学教学可能引起分类的原因大体有四种：①数学概念需要分类定义的；②运用的数学运算性质、法则或定理、公式是分类给出的；③数学问题所得出的结论有多种可能的；④含参类数学问题中的参变量的取值讨论的。解题中如果能够注意渗透分类讨论思想往往能使复杂问题简单化，让解题思路更加清晰明了。在近几年中考数学压轴题中，分类讨论型问题常常结合开放探究型问题一起考查，使题型更加错综复杂。但不论是在分类中探究，还是在探究中分类，都应注意培养缜密的思维，对问题进行全面衡量，细致分类，使复杂的问题得到清晰、完整、严密的解答，进一步提高学生分析问题、解决问题的能力，使学生在解题实践中培养较高的数学素养。

初中数学的所有知识点都可能涉及知识点，解决关键在于弄清引起分类的原因，明确要分类讨论的对象与标准，分不同情况各个击破，再将不同结论归纳总结，综合得出最后正确结论，这其实就是一个总—分—总的过程。分类思想是一种比较常用的数学思想，通过对这类题型的训练，对培养学生思维的逻辑性、探索性、综合性，提高学生学习兴趣，都有很好的作用，这种严谨的思维品质也必将对学生的今后的发展产生深刻影响。

［1］初中数学教材中分类思想的探讨［2013-04-08］.［DB/OL］.http://www.doc88.com/p-8498776030755.html.

［2］邓国勋.初中数学教材中分类思想的培养［J］.中学教学参考，2006(23).

［3］石生明.中考数学复习讲练测［M］.陕西：陕西师范大学出版社，2008.

G623.5

A

1673-9884（2016）011-0042-03

2016-05-30

戴灿阳（1976-），男，福建南安人，南安市康美中学中级教师。