欧拉角姿态解算的改进
2018-05-21野莹莹张艳珠邹心宇
野莹莹,张艳珠,邹心宇,陈 蕾,左 越
(沈阳理工大学自动化与电气工程学院,辽宁 沈阳110159)
姿态解算在飞行器动力学计算中具有举足轻重的地位。姿态解算的精度和速度会直接影响飞行控制算法的稳定行、可靠性和实现的难易程度,因此对飞行器姿态解算方法的研究具有重要意义。目前,通常采用陀螺仪获得飞行器的姿态角,但是长期测量精度较差,因此需要对陀螺仪的输出数据进行有效的处理才能获得可靠和稳定的姿态角信息,陀螺仪输出的数据通过运动学微分方程可以推导出飞行器的微分方程[1]。
在飞行力学研究中,用于求解欧拉角的微分方程中包含大量的三角运算,会给实时解算带来了一定的困难,而且存在的“GimbalLock”现象[2]。所以欧拉角方法不适用于全姿态飞行器的姿态确定。本文引入四元数,进而使用了一阶龙哥库塔求解四元数微分方程,最终转化为欧拉角得到飞行器空中姿态。
1 坐标变换
首先进行坐标变换,利用欧拉角描述一次平面旋转,见图1.

图1 坐标系间的变换关系[3]
设坐标系绕旋转α角后得到坐标系X2OY2,空间中有一个矢量在坐标系X1OY1中的投影为rx2,在X2OY2内的投影为ry2,由于旋转绕进行,所以Z坐标未变,即有:

上面仅仅是绕一根轴的旋转,三维空间中的欧拉角要进行三次这样的坐标旋转变换,得到(2)式。

2 求解姿态角
经过三次旋转,到了一个表示旋转的方向余弦矩阵。再利用欧拉微分方程,进行下面的姿态解算:

式(3)左边是本次更新后的翻滚角 Φ(roll)、俯仰角 θ(pitch)、偏航角 ψ(yaw),式(3)右边是上个周期测算出来的角度,角速度单位为弧度,计算间隔时T陀螺角速度。因此求解这个微分方程就能解算出当前的欧拉角。
3 利用四元数求解姿态角
利用四元数代替欧拉角对方向余弦矩阵的描述:

引入一阶龙哥库塔方程并求解。最后根据四元数方向余弦阵和欧拉角的转换关系,把四元数转换成欧拉角,进而得到用四元数表示的四轴飞行器空中姿态参数 γ、θ、ψ:

4 实验结果
根据上述推算方法进行实验,并在飞行器上位机上采集到如下数据。结果如图2和图3所示。其中加速度曲线横坐标表示时间(ms);纵坐标表示加速度(g)。陀螺仪曲线横坐标表示时间(ms);纵坐标表示陀螺仪(%)。

(续下图)
(接上图)
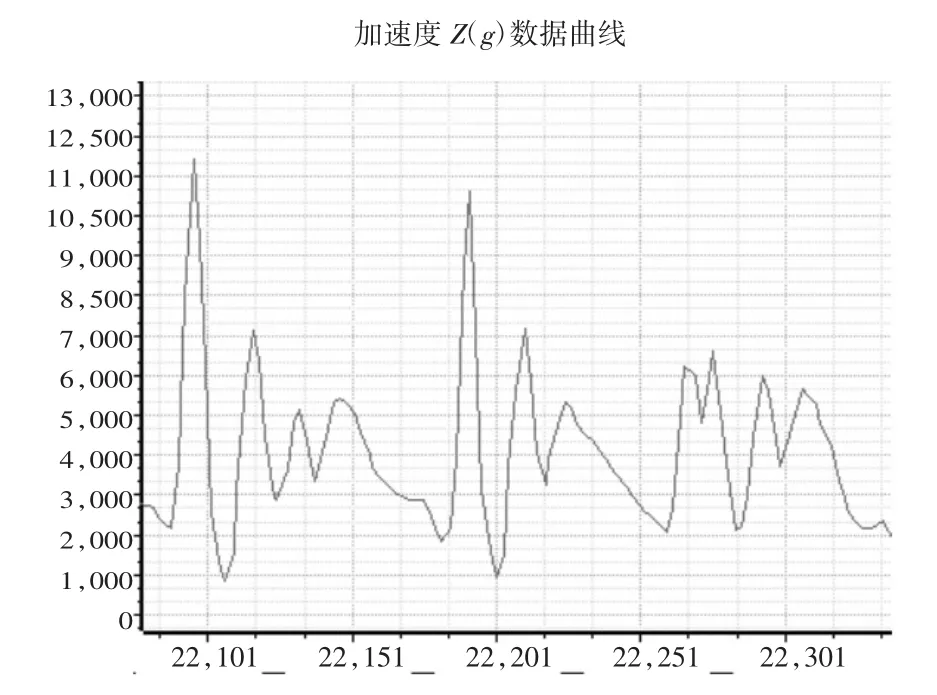
图 2 分别为加速度 X(g)、Y(g)、Z(g)曲线
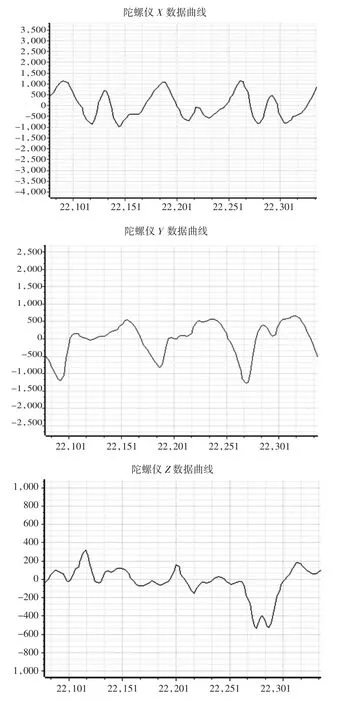
图3 陀螺仪X、Y、Z轴曲线
5 结束语
本文对欧拉角的姿态解算进行改进,引入四元数进行解算。一方面避免了利用欧拉方程中的复杂三角运算,另一方面解决了俯仰角为90°时方程式会出现的“GimbalLock”现象。经过试验验证该方法进行姿态解算效率高而且结果准确,在姿态解算领域有良好的应用前景。
参考文献:
[1]张 帆,曹喜滨,邹经湘.一种新的全角度四元数与欧拉角的转换算法[J].南京理工大学学报(自然科学版),2002(04):376-380.
[2]赵学杰.数值方法中Runge-Kutta方法改进的探讨[J].衡水学院学报,2014,16(04):23-26.
[3]吕志鹏,伍吉仓,公 羽.基于四元数的大旋转角坐标变换模型的改进[J].武汉大学学报(信息科学版),2016(02):1-7.
