立足常法通法 兼顾巧法妙法——一道调考题的解法研究



立足常法通法兼顾巧法妙法
——一道调考题的解法研究

梅磊

(湖北省武汉市黄陂区第六中学，430300)

一道好题,可以撩动学生自主探究的兴趣,升华认知,欲罢不能;可以煽动学生联想的翅膀,类比体验,乐不思蜀;可以拨动学生创新的激情,艰难求索,义无反顾.它也正是数学研究性学习的好素材.

武汉市2015届高中毕业生调考数学选择题的压轴题如下：

题目过点A(-2,3)作抛物线y2=4x的两条切线l1,l2，与y轴分别交于点B,C,则∆ABC的外接圆方程为()

(A)x2+y2-3x-2y+1=0

(B)x2+y2-2x-3y+1=0

(C)x2+y2-3x-4=0

(D)x2+y2+x-3y-2=0

作为选择题,将点A(-2,3)的坐标代入四个选项,可知答案为D.

如果此题不是选择题,或者设计点A的坐标满足全部四个选项呢?

笔者就此题的解法进行研究,得到解答此题的常法、通法、巧法和妙法.

解法1设所作切线方程为y-3=k(x+2),与抛物线方程y2=4x联立,可得k2x2+(4k2+6k-4)x+4k2+12k+9=0.

由Δ=0,得2k2+3k-1=0,解得

从而线段BC的垂直平分线方程为

①

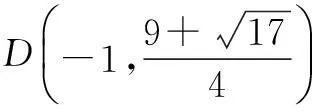
②

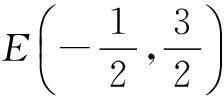
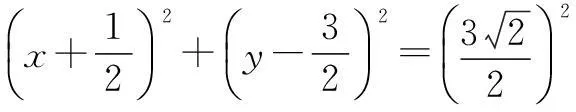
即x2+y2+x-3y-2=0.

评注解法1是常规常法,思路自然清晰,但运算十分繁琐,不可取.

解法2设切线方程为y-3=k(x+2),与抛物线方程y2=4x联立,可得

ky2-4y+8k+12=0.

由Δ=0,得2k2+3k-1=0,从而

不妨设直线lAB的方程为y-3=k1(x+2).令x=0,得y=2k1+3,故B(0,2k1+3).

同理可得C(0,2k2+3).

设∆ABC的外接圆方程为

x2+y2+Dx+Ey+F=0.

令x=0,得

y2+Ey+F=0,

则E=-(y1+y2)

=-2(k1+k2)-6

=-3,

F=y1y2

=4k1k2+6(k1+k2)+9

=-2.

将点A的坐标代入,可得D=1.

所以∆ABC的外接圆方程为

x2+y2+x-3y-2=0.

评注解法2是通性通法,利用整体思想,设而不求,运算相对简单.

下面给出解答此题的巧法和妙法.为此，先给出抛物线切线的两个常用性质：

性质1过抛物线y2=2px(p>0)上一点G(x0,y0)的切线方程为y0y=p(x+x0).

性质2过抛物线y2=2px(p>0)外一点A(x0,y0)作两条直线AM、AN，与此抛物线相切于点M、N,则切点弦MN所在直线的方程为y0y=p(x+x0).

解法3设直线l1,l2与抛物线y2=4x相切于点M(x1,y1)、N(x2,y2),则由性质2知直线MN的方程为3y=2(x-2).将其与抛物线方程y2=4x联立,可得y2-6y-8=0,则y1+y2=6,y1y2=-8.

设∆ABC的外接圆方程为

x2+y2+Dx+Ey+F=0.

令x=0,得y2+Ey+F=0,则

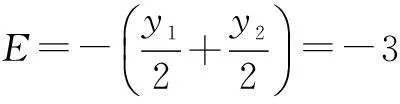
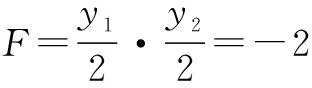
将点A的坐标代入,可得D=1.

所以∆ABC的外接圆方程为

x2+y2+x-3y-2=0.

评注解法3是巧法,利用有关抛物线的切线的两个常用性质,进一步减少了运算量.

定义如果一个三角形的三边所在直线都与某圆锥曲线相切,则称该三角形是此圆锥曲线的外切三角形.

性质3抛物线外切三角形的外接圆过焦点.

推论过抛物线y2=2px(p>0)外一点A(x0,y0)作两条切线l1,l2，与y轴分别交于点B,C,点F是抛物线的焦点,则线段AF是∆ABC的外接圆的直径.

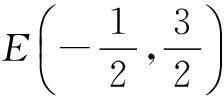
故∆ABC的外接圆方程为

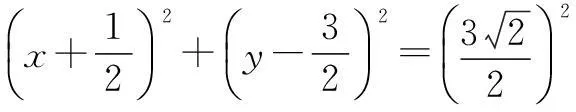
即x2+y2+x-3y-2=0.

评注解法4是妙法,利用抛物线外切三角形的性质,找到是试题的命题基础,可谓秒杀方法.

至此,通过对一道调考题深入研究,我们不但得到了解答此题的常法、通法、巧法和妙法,而且感受到了数学研究的乐趣.不放过那些可能作为知识、能力、思想、方法考查的载体的题目,深入研究可能被利用的题目,充分发现它的价值,发挥它的潜在功能,这是我们教学过程中一定要做的工作.