不确定环境下铁路客运量预测方法



不确定环境下铁路客运量预测方法

齐杉1，李夏苗1，吴慧山2，苟敏1，赵杰群1

(1. 中南大学 交通运输工程学院，湖南 长沙 410075；

2. 江苏省交通规划设计院股份有限公司，江苏 南京 210014)

摘要:合理预测客运量是铁路部门制定列车开行方案及组织管理的基础，为降低传统预测结果误差较大带来的决策风险，基于系统动力学，分析影响客运量的主要因素，利用逐步回归方法提取了GDP、铁路营业里程和民用汽车拥有量3个关键自变量，运用模糊多元回归预测理论，建立铁路客运量中长期预测模型，相应客运量的值由传统单一值变为区间值，函数图像变为“带”状，这种结果更加符合不确定环境下的实际情况。根据国家统计局公布的1990~2012年中国铁路相关数据，对模型的拟合效果进行了检验，并以2013年的数据为依据对客运量进行预测。结果表明：1990~2012年各拟合中心值与实际值误差均在5%以内，且实际值对拟合区间值的隶属度均在0.5以上，2013年预测中心值与实际值误差为4.74%且实际值在预测区间之内。

关键词：铁路运输；旅客发送量；模糊预测；系统动力学；模糊多元回归模型

交通运输系统是一个复杂系统，系统内部从规划设计到组织管理都必须具有前瞻性，交通预测也应运而生。客运量预测是交通预测的重要组成部分，在规划设计层面上，客运量预测可以帮助决策者判断一个项目是否值得投资，一个车站是否值得设置；在组织管理层面上，对未来若干年的客运量及其发展趋势进行预测，可以帮助管理者预知未来可能发生的情况，有效地组织和管理旅客运输。客运量的预测方法是指根据客观事物的发展趋势和变化规律，对客运量未来发展趋势或状态做出科学的推测与判断所采用的方法。客运量预测存在2种不确定性，即模型的不确定性和外生变量产生的输入不确定性。传统的客运量预测模型中包含大量假设，通过这些假设使得不确定因素变成相对确定的，预测得到的结果是一概率最大的值，可称为“点估计”。Flyvbjerg[1]统计了14个国家的210个交通项目，其中27个是铁路项目，其余为公路项目。研究表明90%的铁路项目客运量都是过高估计的，平均过高估计106%；50%的公路项目误差在20%左右。由此可见，现有“点估计”的预测结果与受到诸多不确定因素影响的实际客运量相比误差较大，使决策具有一定的风险[2]，故对交通运输系统的规划设计和运营管理来说，在未来不确定的环境下，掌握客运量变化范围更有利于科学决策。

本文以中国铁路客运量的增长变化为研究对象，运用系统动力学对客运量的影响因素定性分析并定量筛选以确定关键影响因素，选择模糊相关回归方法对客运量波动范围进行预测，建立客运量中长期预测模型，使预测结果不仅有最大概率的中心值，同时还具有乐观上限值和悲观下限值。

1)客运量确定性预测方法

传统的客运量预测方法有十几种，分为定性预测与定量预测2大类。定性预测包括：用户调查法、类比法和专家调查法3种。定量预测方法大致可分为2种：因果关系分析的预测方法和以时间为参数的预测方法。基于因果分析预测方法是通过对历史数据的仔细分析，找出客运量与相关的社会经济变量之间的制约关系，根据影响因素对未来客运量进行预测。基于时间参数的预测方法是将客运量的历史数据按照时间顺序排列，分析序列随时间的变化趋势，并建立数学模型进行外推的定量预测方法。路小娟等[3]用遗传算法对BP神经网络进行改进，并对客运量进行预测。李凯等[4]用正弦函数描述了重力模型参数的波动规律，改进了原有重力模型将参数标定为常数的缺陷。张亚平等[5]采用IWOGA算子将三次指数平滑、GM(1,1)预测和BP神经网络结合起来，建立组合预测模型。

2)客运量不确定性预测方法

客运量不确定性预测方法是以传统确定性预测方法为基础，结合一些新兴的数学方法进行预测，以弥补传统预测方法的不足。李夏苗等[6]提出了基于模糊时间序列方法的客运量预测模型，并对OD客流表进行反推。初连禹等[7]用神经网络实现对模糊规则的记忆，设计了基于模糊神经网络的实时交通流量预测系统。单也[8]建立了模糊相关回归预测模型对交通量不确定性进行区间度量，并实现了区间路段阻抗下最短路的计算。赵建有等[9]提出了基于模糊线性回归模型的公路货运量预测方法。余少鹤等[10]运用模糊线性回归分析方法,建立编组站运营指标的模糊预测模型。De等[11]总结了近年来国外交通量不确定性预测的部分研究成果。

传统客运量预测方法结果误差较大，无法适应复杂的交通运输系统，虽然在道路运输中存在客运量不确定性预测研究，但其在运用多元相关回归方法预测过程中，缺乏选取相关影响因素作为自变量的理论依据。

1铁路客运量因果关系分析

铁路客运量受多个因素的驱动和影响，在中长期预测中，多元回归分析法能够较好的反映出客运量与影响因素之间的关系，被广泛应用。为使选取的影响因素更加合理，本文运用系统动力学分析法对影响铁路客运量的主要因素进行定性分析，采用统计学分析软件SPSS对具有多重共线性的影响因素进行筛选，选出若干关键影响因素建立多元回归模型进行预测。

系统动力学分析法是一种非线性统计回归的分析方法，通过对系统要素因果关系的分析，建立系统动力学模型，使各要素间的因果关系得到直观展现，把握系统的运行规律[12]。本文利用系统动力学进行分析，得出铁路客运量主要影响因素间的因果关系。影响铁路客运量最主要的因素是客运需求和客运供给，铁路客运需求受到人口数量和国内生产总值等因素的影响，而铁路客运供给主要受铁路营业里程的影响。经过分析，建立铁路客运量的因果关系图，如图1所示。

图1　铁路客运量因果关系图Fig.1 Causality diagram of railway passenger traffic volume

图中“+”含义为两者之间是正反馈关系，如“人口数量”与“铁路客运需求”，“人口数量”的增加会促进“铁路客运需求”的增加，“-”含义为两者之间是负反馈关系，如“铁路客运供给”与“铁路客运短缺”，“铁路客运供给”的增加会促使“铁路客运短缺”减少。

2关键影响因素的选取

多元回归模型要求所有自变量互不相关，故需剔除存在多重共线性关系的因素，并且检验所有因素与客运量是否存在较强的相关性。以国家统计局官网公布的1990—2012年我国铁路客运量及GDP、居民消费水平、年末总人口、铁路营业里程、民用汽车拥有量、铁路运输固定投资的历史数据为样本数据，利用SPSS软件进行多重共线性诊断，结果如表1所示。

表1　多重共线性诊断结果

由表1可以看出，4，5，6和7等4个维数的特征值接近于0，且条件索引大于30，说明变量间存在严重的共线性，且相关系数矩阵中“年末总人口”与“民用汽车拥有量”数值接近于1，二者存在着多重共线性。为挑选出较合适的变量，本文利用SPSS软件进行逐步回归分析，分析结果见表2。

表2　逐步回归法分析结果

由表2可以得出，选取“民用汽车拥有量”、“铁路营业里程”和“GDP”作为预测客运量的关键自变量是合理的。

3模糊多元回归模型

传统多元线性回归模型[13]如下：

Y=A0+A1X1+A2X2+…+AnXn

(1)

式中：Y为因变量；A0~An为回归系数；X1~Xn为自变量。

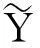
模糊多元回归法中几个重要的定义：

1)对称三角模糊数

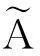
2)隶属度函数

X→[0,1]

(2)

(3)

3)H水平截集

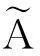
4客运量预测模型的建立

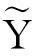
4.1模型的建立

设铁路客运量为Y，受多个因素影响，建立模糊多元回归模型如下：

(4)

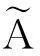
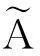
(5)

(6)

(7)

(8)

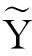
4.2模型的求解

根据模糊回归分析理论，按以下原则对模糊多元回归模型进行求解。

1)模型全体模糊系数的模糊幅度之和最小，即要满足的值最小化。

(9)

2)对于给定的置信水平H，需保证Yk的隶属度全部大于H，通常称为“H水平截集”，表示模糊回归模型对给定的实验数据的拟合精度。因此，对于一定的置信水平H，必须保证覆盖所有的观测数据Yk，即满足

(10)

根据上述原则，将模糊多元回归问题转化为多元规划问题，求解形式如下：

(11)

(12)

其中，式(11)为目标函数，式(12)为约束条件，利用MATLAB软件求解多元规划方程，得到模型中各个模糊回归系数的值。

4.3模型的求解结果分析

对于求解结果，需重新判断模型的形式，解的形式有以下3种：

4.4结果的转化

(13)

根据上式，在置信水平H的条件下，按照区间数的运算法则，模型对客运量拟合的区间值可表示为：

(14)

拟合得到客运量在一定置信水平下的区间值，该区间值包含了客运量预测的不确定信息，更符合客运量预测的实际情况。

4.5结果的评价

对于模型求解的结果，需要对模型拟合的中心值和在一定置信水平下的区间值进行评价[15]。

1)拟合中心值的评价

模型求解后，应评价模糊系数中心值对实际值拟合的优劣，以中心值为回归系数的模型拟合值与实际值Yk之间相对偏差记为Ωk，如式(15)，若Ωk在30%以内，即认为拟合是可以接受的。

(15)

2)拟合区间值的评价

(16)

5算例分析

5.1建立模糊多元回归模型

应用SPSS逐步回归法选取的GDP、铁路营业里程和民用汽车拥有量3个关键变量，相关数据见表1，建立模糊回归方程如下：

(17)

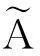
5.2模型参数的求解

取置信水平H=0.5，通过MATLAB软件编程求解模糊多元回归方程，结果见表3。

表3　模型回归系数的中心值及模糊幅度

由表3可知，4个自变量的中心值ai均不为0，说明4个自变量都与因变量相关，铁路营业里程的模糊幅度bi不为0，说明客运量的不确定性与其有极大的关系。

建立模糊多元回归方程：

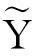
(18)

在置信水平H=0.5下，将三角模糊数转化为该置信水平下的区间数，客运量的区间形式可以表示为：

[-25 358.757 4，-22 180.035 7]x2+1.844 7x3

(19)

5.3回归结果分析与评价

将1990~2012各年GDP，铁路营业里程和民用汽车拥有量的数据代入模糊方程(18)中，得到客运量拟合中心值和实际值的对比结果见表4。

表4　拟合中心值与实际值的对比结果

从表4中的数据可以看出，模型拟合中心值与实际值之间的相对偏差大致在5%以内，远低于30%[15]，拟合效果较好，拟合中心值与实际值的对比结果见图2。

图2　拟合中心值与实际值对比Fig.2 Comparison between the fitting central values and the actual values

在置信水平H=0.5的条件下，将表1中1990—2012各年GDP、铁路营业里程和民用汽车拥有量的数据代入模糊方程(19)中，则模型对客运量拟合的模糊值转化成区间值，拟合区间上、下限值与实际值的对比结果见表5。

表5拟合区间值与实际值对比结果

Table 5 Comparison between the fitting interval values and the actual values万t

年份实际值/万人拟合中心值/万人区间下限值/万人区间上限值/万人隶属度μY(Yk)199095712.0096403.8387201.44105606.230.92199195080.0097780.4688593.96106966.970.71199299693.0098945.5389711.34108179.710.921993105458.00100801.1991487.53110114.840.501994108738.00104381.3995004.16113758.620.541995102745.00100694.0790776.46110611.680.79199694797.0098335.1488020.19108650.090.66199793308.0098552.9188063.13109042.690.50199895085.0099600.7589047.40110154.110.571999100164.0099234.1588521.86109946.440.912000105073.0099620.4888701.57110539.390.502001105155.00100138.7888997.36111280.200.552002105606.0099892.2888464.78111319.780.50200397260.00103061.2091458.87114663.540.502004111764.00108337.6696512.81120162.500.712005115583.00115194.18103210.40127177.960.972006125655.80122707.12110453.15134961.100.762007135670.00138535.09126138.08150932.110.772008146192.85152067.31139400.11164734.520.542009152451.19150062.69136473.66163651.730.822010167609.02160361.66145866.69174856.630.502011186226.07183489.47168676.63198302.320.822012189336.85192566.64177054.48208078.800.79

图3　拟合区间值与实际值拟合程度Fig.3 Comparison between the fitting interval values and the actual values

以2013年为例，由国家统计局官网公布的数据可知，2013年GDP为58.801 88万亿元、铁路营业里程为10.31万km、民用汽车拥有量为12 670.14万辆，将这3个数据分别代入式(18)和(19)中，对2013年客运量进行预测，得到2013年预测客运量的中心值为200 620.54万人，模糊区间为[184 234.23，217 006.85]，而2013年实际客运量为210 596.92万人，实际值在预测区间之内，预测中心值与实际值的误差为4.74%，在容许范围之内。

根据国家年初制定的发展计划，可预测铁路行业当年客运量及其波动范围。以2014年为例，由于国家统计局官网尚未公布官方数据，故将新闻报道中相关数据作为依据预测客运量，其中GDP约为63.646 3万亿元，铁路营业里程突破11万公里(取11)，民用汽车拥有量约为15 447万辆(取16 000)，铁路客运量约为232 000万人。为保证模型预测的精度，将2013年相关数据加入到样本数据中，对模型参数进行更新，再将2014年数据代入，即可得出2014年铁路客运量中心值约为221 376万人，波动区间约为[208 950，234 183]，实际客运量与预测值误差为4.58%，且实际值在预测区间内。

6结论

1)利用系统动力学对影响铁路客运量的主要因素进行分析，通过定性与定量结合的方法，挖掘出GDP、铁路营业里程和民用汽车拥有量3个关键影响因素，为模糊多元线性回归模型中自变量的选取提供有力的理论支撑。

2)运用模糊相关回归预测法对我国铁路客运量进行中长期预测，通过给出预测结果的模糊变化区间，即预测结果存在一个乐观的上限值和一个悲观的下限值，解决了变量之间关系不明确、数据不精确等不确定问题对预测结果的影响，降低了传统方法带来的决策风险，使预测结果更加科学合理，更符合复杂系统无法准确预测的实际。

3)将系统动力学与模糊多元回归预测方法相结合，既体现了客运量变化的驱动因素，同时对未来不确定环境变化有回应，有助于决策者更好地进行规划设计和组织管理。

4)为保证预测的准确性，可将官方公布的最新数据加入样本数据中，更新模型参数。

参考文献：

[1] Matas A, Raymond J L, Ruiz A. Traffic forecasts under uncertainty and capacity constraints [J]. Transportation, 2012,39(1):1-17.

[2] Bain R. Error and optimism bias in toll road traffic forecasts [J]. Transportation, 2009,36(5):469-482.

[3] 路小娟,马宝峰,张武娟. 铁路客流量预测分析与研究[J] .兰州交通大学学报, 2013,32(6):28-31.

LU Xiaojuan, MA Baofeng, ZHANG Wujuan. Prediction analysis and research on railway passenger traffic volume [J]. Journal of Lanzhou Jiaotong University, 2013,32(6):28-31.

[4] 李凯,马驷,许传粉,等. 改进重力模型在铁路客运量预测中的应用 [J]. 石家庄铁道大学学报(自然科学版), 2014,27(4):94-97.

LI Kai, MA Si, XU Chuanfen, et al. Application of improved gravity model in the railway passenger traffic volume forecast [J] .Journal of Shijiazhuang Tiedao University(Natural Science Edition) 2014,27(4):94-97.

[5] 张亚平,武宁宁. 基于IWOGA算子的公路客运量组合预测模型 [J]. 武汉理工大学学报(交通科学与工程版), 2013,37(6):1153-1157.

ZHANG Yaping, WU Ningning. A combination forecasting model of highway passenger transportation volume based on IWOGA [J]. Journal of Wuhan University of Technology(Transportation Science & Engineering), 2013,37(6):1153-1157.

[6] 李夏苗,曹尧谦,王慧晶,等. 基于模糊预测的高速铁路客流OD表的推算方法 [J]. 交通运输系统工程与信息， 2014,14(5): 93-99.

LI Xiamiao, CAO Yaoqian, WANG Huijing, et al. An estimation method of passenger OD flows of high-speed railway network based on fuzzy predication [J]. Journal of Transportation Systems Engineering and Information Technology, 2014,14(5): 93-99.

[7] 初连禹,杨兆升. 基于神经网络的实时交通流量模糊预测 [J]. 中国公路学报, 1998,11(增1): 78-82.

CHU Lianyu, YANG Zhaosheng. Real-time traffic volume prediction based on fuzzy neural network [J]. China Journal of Highway and Transport, 1998,11(Suppl 1): 78-82.

[8] 单也. 出行生成量不确定时的交通需求预测研究 [D]. 哈尔滨：哈尔滨工业大学, 2012: 20-25.

SHAN Ye. Research on traffic demand forecast with uncertainty trip generation[D]. Harbin: Harbin Institute of Technology, 2012: 20-25.

[9] 赵建有,周孙锋,崔晓娟,等. 基于模糊线性回归模型的公路货运量预测方法 [J]. 交通运输工程学报, 2012,12(3):80-85.

ZHAO Jianyou, ZHOU Sunfeng, CUI Xiaojuan, et al. Predictive method of highway freight volume based on fuzzy linear regression model [J]. Journal of Traffic and Transportation Engineering, 2012,12(3):80-85.

[10] 余少鹤,李夏苗. 基于模糊线性回归分析的编组站运营指标预测方法 [J]. 铁道学报, 2003, 25(5): 8-13.

YU Shaohe , LI Xiamiao . Method for prediction of the operating indices of marshalling station based on fuzzy linear regression analysis [J].Journal of the China Railway Society , 2003, 25(5): 8-13.

[11] De J G, Daly A, Pieters M, et al. Uncertainty in traffic forecasts: literature review and new results for The Netherlands [J] . Transportation, 2007,34(4): 375-395.

[12] 王其藩. 系统动力学 [M]. 北京：清华大学出版社, 1994:31-46.

WANG Qifan. System dynamics [M]. Beijing: Tsinghua University Press, 1994:31-46.

[13] 李安贵, 张志宏, 段凤英. 模糊数学及其应用 [M]. 北京: 冶金工业出版社, 1994:232-247.

LI Angui, ZHANG Zhihong, DUAN Fengying. Fuzzy mathematics and application [M]. Beijing: Metallurgical Industry Press, 1994:232-247.

[14] Giachetti R E, Young R E. Analysis of the Error in the Standard Approximation Used for Multiplication of Triangular and Trapezoidal Fuzzy Numbers and the Development of a New Approximation [J]. Fuzzy Sets and Systems， 1997, 91(1): 1-13.

[15] 杜渐. 模糊多元回归模型在运输弹性系数预测中的应用 [J]. 武汉理工大学学报: 交通科学与工程版, 2009, 33(2): 334-335.

DU Jian. Application of fuzzy multiple regression model to transportation elasticity coefficient forecast[J]. Journal of Wuhan University of Technology (Transportation Science & Engineering), 2009, 33(2): 334-335.

(编辑蒋学东)

Prediction method of railway passenger traffic volume under uncertainty environmentQI Shan1, LI Xiamiao1, WU Huishan2, GOU Min1, ZHAO Jiequn1

(1. School of Traffic and Transportation Engineering, Central South University, Changsha 410075, China;

2. Jiangsu Province Communications Planning and Design Institute Limited Company, Nanjing 210014, China)

Abstract:Reasonable prediction of passenger traffic volume is the basis for making train operation plan, organization and management for the railway department. In order to decrease the decision risk caused by traditional prediction result, this paper analyzed the main factors affecting passenger traffic volume based on system dynamics. GDP, railway mileage and the number of civilian car ownership were selected as independent variables using the stepwise regression theory. A predicting method based on fuzzy multiple regression was proposed to establish for predicting the long-term railway passenger volume. It could make the prediction passenger traffic volume change from a traditional single value to interval value and turn the function of the image into a ribbon, which shows a better agreement with the actual situation under uncertainty environment. Some testing work for the fitting effect of the model was done based on the data published by National Bureau of Statistics in China from 1990 to 2012 and forecast passenger traffic volume in 2013. The results show that the errors between the fitting center values and the actual ones are all under 5% while the degree of membership of actual value are all above 0.5 from 1990 to 2012.The error is 4.74% between the prediction center value and the actual one while the actual value is in the prediction interval value in 2013.

Key words:railway transportation; passenger traffic volume; fuzzy prediction; system dynamics; fuzzy multiple regression model

中图分类号：U293.13

文献标志码：A

文章编号：1672-7029(2016)01-0168-08

通讯作者：李夏苗(1963-)，男，湖南茶陵人，教授，博士，从事铁路运输管理、综合交通系统优化、系统分析与优化决策研究；E-mail：xmli@csu.edu.cn

基金项目：国家自然科学基金资助项目(U1334207)

收稿日期：*2015-06-25