方法纷呈迷人眼，思想才能现本质——再谈“等比数列前n项和公式”的推导

☉江苏省常熟市浒浦高级中学吴晓英

方法纷呈迷人眼，思想才能现本质
——再谈“等比数列前n项和公式”的推导

☉江苏省常熟市浒浦高级中学吴晓英

从认知层面看，等比数列前n项和公式在陈述性知识、程序性知识与策略性知识的分类中，属于学生最高需求层次的掌握策略与方法的策略性知识.因此，等比数列的前n项和公式的推导历来是教学的重点与难点，对于此公式的推导教学的探讨也一直没有停息.最近笔者观摩了一堂关于“等比数列前n项和公式”推导的课，这堂课的最大特色就是用到了多种推导方法，并且这些方法并不是无序的堆积与罗列，而是按照一定的思维主线串联起来.下面笔者就以这堂课为载体，谈谈“等比数列前n项和公式”的教学策略.

一、教学过程简介

1.创设情境，提出问题

情境设计：（还款游戏）一个穷人到富人那里去借钱，原以为富人不愿意，哪知富人一口答应了下来，但提出了如下条件：在30天中，富人第一天借给穷人1万元，第二天借给穷人2万元，以后每天所借的钱数都比上一天多一万；但借钱第一天，穷人还1分钱，第二天还2分钱，以后每天所还的钱数都是上一天的两倍，30天后互不相欠.穷人听后觉得挺划算，本想定下来，但又想到此富人是吝啬出了名的，怕上当受骗，所以很为难.请在座的同学思考一下，帮穷人出个主意.

意图：通过这个问题情境，引出对数列S30=1+2+22+…+229求和的思考.为后续一般的等比数列求和公式的推导做好思维上的铺垫.

2.归纳推理，探究规律

由于学生对于这类数列求和比较陌生，所以教师启发学生，能不能利用特殊到一般的思想，利用归纳推理，猜想出求和公式的结构.

方法一：（特殊法）

（1）Sn=1+2+22+…+2n-1.S1=1=2-1，S2=1+2=3=22-1，S3= 1+2+22=7=23-1，…，Sn=2n-1.

这种方法还可以继续推广到其他等比数列求和.

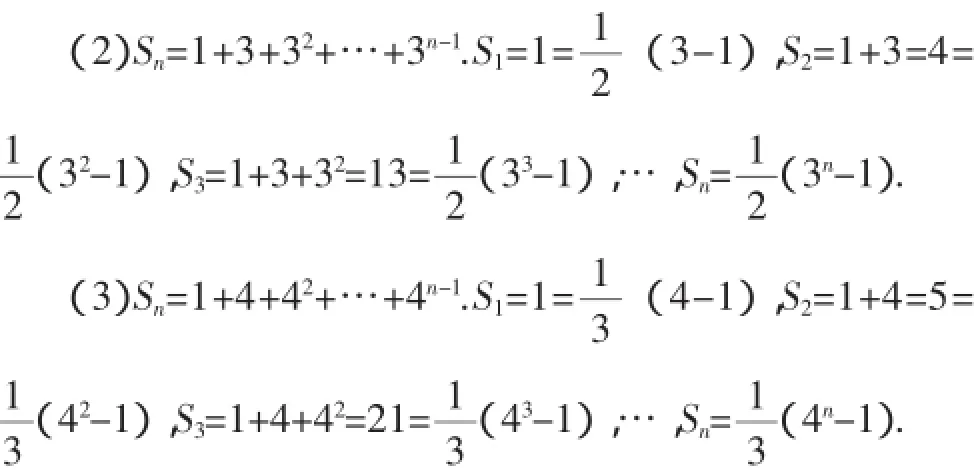
因此，对于一般的等比数列｛an｝的求和，Sn=a1+a2+…1）.当q=1时，Sn=na1.

意图：公式推导的过程应该是学生在课堂上生成的结果，为了达到自然生成的预期，教师尽可能从特殊情况入手，然后引导学生发现潜在的规律.因为有了特殊情形的提示，一般情形下利用错位相减较易得到.

方法二：（逆推法）由Sn=1+2+22+…+2n-1=2n-1，发现｛Sn+1｝是等比数列.也就是说，在原有数列求和的基础加“1”，就可以转化为等比数列.因此

同理，Sn=1+3+32+…+3n-1⇔2Sn=2+2×3+2×32+…+2×

意图：从推导的结论入手，执果索因，从而可以得到启发：在等比数列求和公式两边同时乘以公比q，然后与原来的求和公式作差就可以推得等比数列求和公式.

方法三：（错位相减）Sn=a1+a2+…+an=a1+a1q+…+a1qn-1，则qSn=a1q+a1q2+…+a1qn.

3.方法鉴赏，拓展思维

方法四：（利用合并定理）注意到等比数列每一项都不等于零，由等比数列定义，得，则

方法五：（利用配凑法）Sn=a1+a2+…+an=a1+a1q+…+，整理得（1-q）Sn=

方法六：（整体代换法）Sn=a1+a2+…+an=a1+q（a1+a2+（q≠1）.

点评：本课的最大亮点就是公式推导的方法“多而全”，凡是当前比较流行的方法都作了详细的介绍.这些证明方法也不是无序的罗列，而是通过两个阶段系统的给出.在第一个阶段中利用特殊到一般的思想，通过猜想、分析、类比，从而引出公式证明的重要思想方法——“错位相减法”；第二个阶段的主要目的是证明方法的鉴赏，通过鉴赏不同角度的推导与证明，从而进一步拓展学生的数学思维.

二、方法纷呈迷人眼

本课的证明方法虽多，但细细品味还是发现一些值得商榷的地方.

首先，这些方法是否有必要在一堂课中都得以呈现.方法总有主次重要之分，本课的重点与难点是“错位相减法”.有些方法虽然在等比数列前n项公式的推导中表现出了快捷直观的特点，但不见得具有很大的推广价值.而错位相减法不仅能够推导等比数列前n项和公式，而且对类似“等差乘等比”的数列也能适用.所以，本节课的重心应放在错位相减法的发现与运用上.

其次，这么多的方法其内部究竟有什么联系.看似方法很多，实际上大同小异.掌握了其中一种方法的推导思想，其余的方法学生自然可以想到.不仅如此，这些方法教师讲了学生都能够掌握吗？或者说，这些方法有哪些是学生能够自然想到的？如果学生无法自然想到，那么教师的讲解其实就异化成“灌输”，这是我们在课堂教学中坚决不提倡的.

最后，把技巧与方法作为教学的重点而忽视对求和本质的揭示.一般地，要求和通过相加（手段）实现，但要求和，不仅仅只有通过相加才能实现（辩证思维），求和就是想方设法求出和的结果.因而，从某种意义上来讲，求和就是对和式进行化简，也就是求和的本质是化简.学生若不了解求和的本质，那么了解再多的方法又有何意义.

三、思想才能现本质

那等比数列前n项和公式的教学该如何进行呢？笔者认为，首先明确求和的本质，然后以数学思想为引领，让学生自然发现求和的方向与方法.

1.回顾复习，寻找灵感

先回顾等差数列求和公式的推导过程，明确数列求和的目的就是化简，也就是说把多余的项消去，只保留少数几项.具体操作如下：

第一步，写出求和公式Sn=a1+a2+…+an.

第二步，仅凭一个式子很难实现“消项”，一般情况需要在原理的基础上再构造一个，形成类似方程组的形

第三步，现在问题就转化为解方程组.一般解方程组往往通过上下两个方程相加或相减实现消元.那么对于上述两个方程，直接作差显然不行，因为所有的项都消掉了.直接作和也不行，因为一项也没消掉.到底采取怎样的消项策略，取决于数列本身的形式.根据等差数列的对称性，所以想到采用“倒序相加”的策略.

2.灵活运用，感悟思想

为了加深学生对于错位相减法的认同感，体会此方法的重要作用.我们可以进一步利用错位相减法求“等差×等比”型数列的前n项和.

问题：求数列an=n2n的前n项的和Sn=2+2·22+3·23+…+n2n①.

这个数列的通项是由等差数列和等比数列相乘构成的，因此考虑问题的时候应该从等差数列和等比数列的角度进行分析.从整体上看，这个数列求和与等比数列求和非常接近，但显然不能直接用等比数列求和公式，因为每一项前面的系数不一样.如果能够把求和公式化成类似于Sn=A·2+A·22+A·23+…+A2n的结构就可以用等比数列求和公式了.那如何把系数化成相同呢？因为每一项的系数成等差数列，根据等差数列的定义，后一项和前一项的差都是同一个常数公差.但每一项的次数是不一样的，因此前后两项无法直接相减，若要相减，次数必须一样.

经过以上分析，基本上已经确定了解题的基本框架，就是把各项系数化成一致，转化为等比数列进行求和.而要实现系数一致，首先必须实现次数一致.因此，不妨把第一项乘以公比2，那它就和第二项的次数一样，就可以和第二项作差，同理，第二项乘以公比2就可以和第三项作差了，依次类推，这就相当于在原来的数列求和式子的两端同乘一个公比2，即2Sn=22+2·23+3·24+…+ n2n+1②.接下去把①、②两式子作差，因为只有次数相同才能作差，所以必须要错开，即作差后原来的求和式子就转化为与等比数列求和有关的问题了，即-Sn=，接下去问题就容易解决了.

通过这个问题使学生进一步感悟错位相减法的数学思想：错位的目的是为了能够相减，而相减的目的是为了能够求和.

综上所述，数学推导证明的方法不在于多，而在于“精”，在乎“自然”，在乎融会贯通.F