具有Holling II捕食功能反应的捕食系统奇点的稳定性与极限环的存在性
2016-02-27武芳
武芳
(南京财经大学应用数学学院,江苏南京210023)
具有Holling II捕食功能反应的捕食系统奇点的稳定性与极限环的存在性
武芳
(南京财经大学应用数学学院,江苏南京210023)
本文研究了一类具有HollingⅡ型捕食功能反应的捕食系统,对系统进行了定性分析,给出了该系统奇点稳定性的相关讨论结果、系统包含正奇点的全局稳定性及极限环的存在性的证明.
Holling II型捕食系统;奇点;稳定性;极限环
自上世纪以来,各种生物学模型受到广泛的关注,种群之间的捕食关系也吸引了各个学科学者们的目光,许多学者对此已经做了大量的研究工作.对于两种群相互作用的具有功能反应函数的食饵-捕食模型,人们往往关心的是系统是否有孤立的周期解,换句话说就是系统是否有唯一的极限环,因为稳定的极限环对应稳定的种群的生态平衡.稳定的平衡态对种群的生存具有十分重要的意义.
文献[1]研究了具有Holling I型功能反应函数的捕食者-食饵系统,考虑当功能反应函数是HollingⅡ型时,即系统为:

时,对系统的平衡点及极限环进行讨论.本文考虑当系统为具有Holling II捕食功能反应的捕食系统

时,对系统奇点的稳定性及极限环的存在性进行讨论.其中K,A,B,Ci,Di(i=1,2)都是正的常数.
1 简化参数
为了方便起见,首先对系统(2)进行参数化简.
令u=gx,v=hy,τ=mt,则有:


则(3),(4)式可简化为:
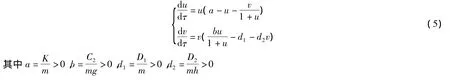
为了与通常的记法一致,用x,y替换u,v,于是系统(2)简化为:

其中a,b,d1,d2均为大于零的参数.
2 系统所有可能的奇点
于是所有可能的奇点为:O(0,0)E1(a,0)E*(x*,y*)
其中x*,y*满足:

即两条直线l1,l2的交点为E*(x*,y*),
由方程l1可得解为y1=(1+x)(a-x);由方程l2可得解为

3 奇点的局部稳定性
若E*(x*,y*)为正奇点(即存在且为正),则0<x*<a,
又

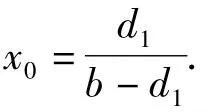
性质1若(H1)成立,则(3)存在唯一的正奇点E*(x*,y*).
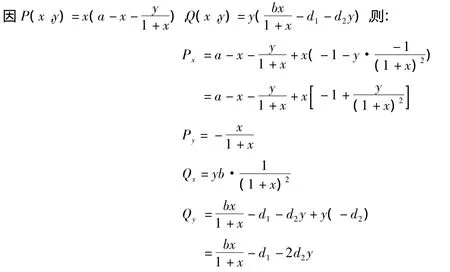
下面针对每一个可能的奇点讨论其稳定性.
为了方便下面的证明,首先给出如下说明:
若线性系统在奇点A处的特征方程为λ2+pλ+q=0,若特征方程有2个异号的实特征根,那么奇点为鞍点,不稳定.若特征方程有2个同号的实根,那么奇点为结点,如果特征方程中的p>0,q>0,则结点是稳定的;如果p>0,q>0,则结点不稳定.若特征方程有一对共轭复根,则奇点为焦点.若特征方程有一对纯虚根那么奇点为中心焦点[1].详见文献[2].

所以O(0,0)为鞍点,不稳定.
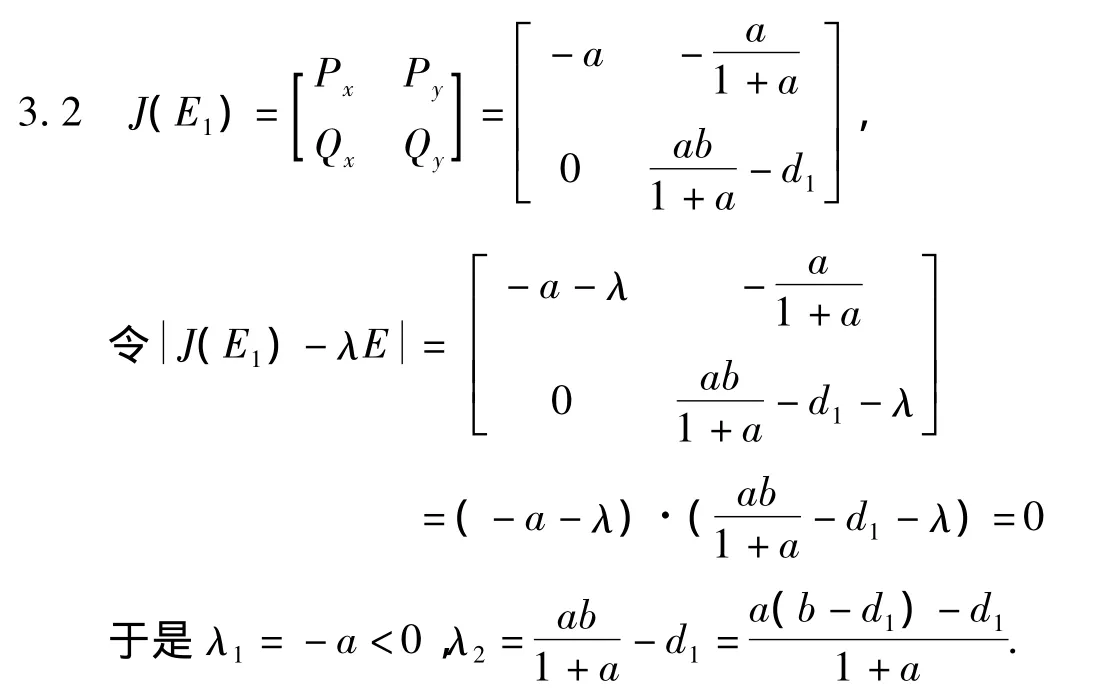
性质2(i)若a(b-d1)>d1,则λ2>0,E1(a,0)为鞍点,不稳定(但此时E*存在);
(ii)若a(b-d1)<d1,则λ2<0,E1(a,0)为结点,稳定(但此时E*不存在).

则有:

令p=a2-d1+x*(1-a1),q=(a1-1)x*·(d1-a2)+a1a2,则(7)式可化为:

令f(x)=2x2+(1+b-d1-a)x-d1,考虑f(x*)的正负:

令f(x)=0,得两根:




(i)当p2-4q>0时,λ1+λ2=-p,λ1·λ2=q>0,则λ1,λ2两根同号:



则E*(x*,y*)是稳定的,但不是渐进稳定的.
注由(i),(ii),(iii)可以总结出:
4 包含正奇点的全局稳定性
取V函数:

于是沿着系统(3),V函数对时间t的导数为:
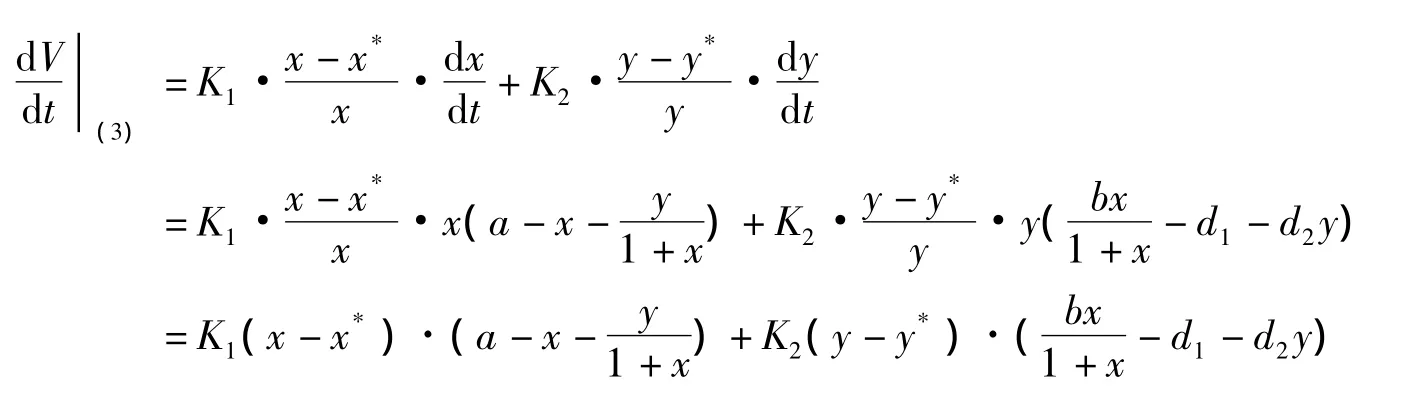
由于体育活动需要场地与体育器材,就需要具备一定经费的投入,只有在体育方面进行经费的投入,幼儿园才能进行体育活动[3]。经过对成都市龙府幼儿园的调查,发现幼儿园的体育方面的经费一般来自政府的投入和自筹,而幼儿园在体育方面的经费与幼儿园的类别有非常大的关系,成都市幼儿园在体育活动经费的投入方面出现不均衡的情况,一些民办幼儿园由于体育方面的经费不足,导致活动场地和体育器材都出现短缺的情况,这种情况的出现导致幼儿健康教育方面的目标很难完成。
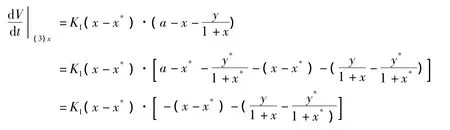
而

于是

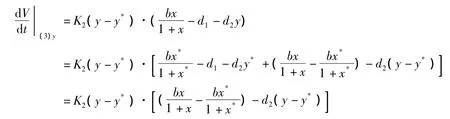
而

于是
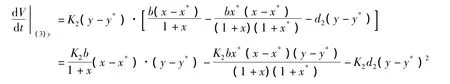
因此


取K1=b,K2=1,则:

其二次型矩阵为:
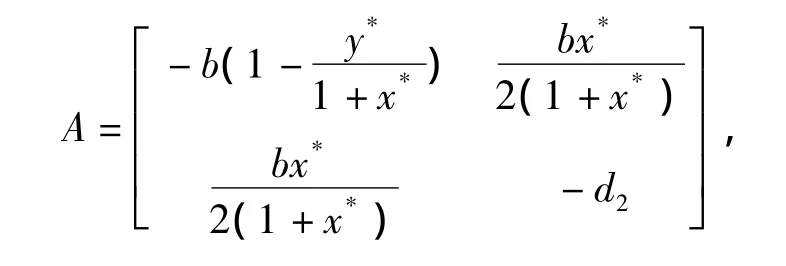
5 包含正奇点的极限环的存在性

由以上结果可知,在(H2)条件下,E*存在但不稳定.
取L1=x-a=0,∀y>0,有:

故当轨线与x=a相遇时,均从直线x=a右方穿入左方;
∀x∈[0,a],有:

6 使用Matlab软件进行数值模拟,验证奇点的局部稳定性
(1)已知O(0,0)为鞍点,不稳定.取a=2,b=3,d1=2,d2=4,则图形如图1所示,显然O(0,0)不稳定.

图1
(2)E1(a,0)点的局部稳定性,如:
取a=4,b=2,d1=d2=1,则如图2所示.
很显然,此时E1(a,0)不稳定;
取a=1,b=3,d1=2,d2=1,则稳定性如图3所示,此时E1(a,0)稳定于(1,0)点.

图2
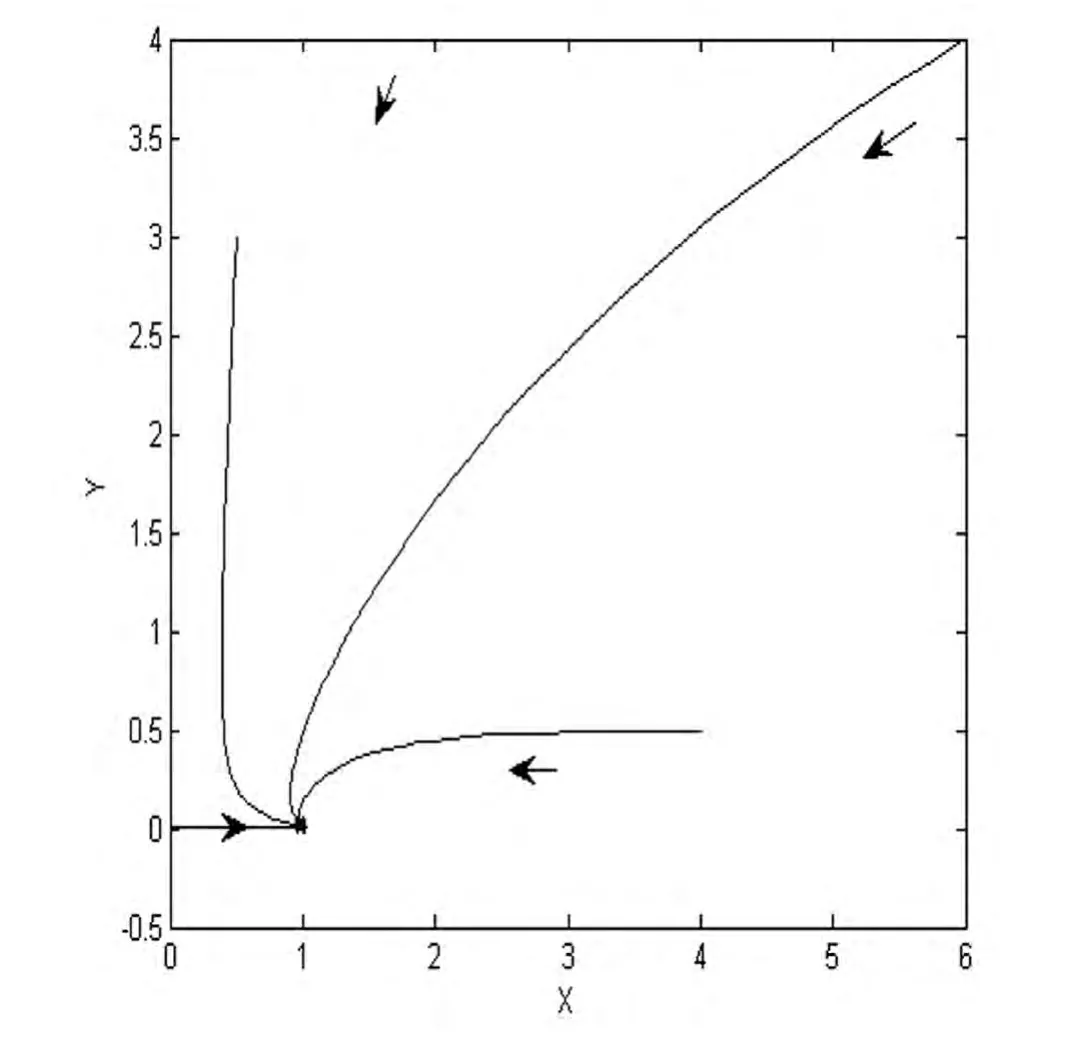
图3
取a=2,b=2,d1=1,d2=1.则E*(x*,y*)渐进稳定,如图4所示.
取,b=4,d1=1,d2=2,则E*(x*,y*)渐进稳定,如图5所示.

图4

图5

图6
[1]范学良,雒志学,张宇功.一类具HollingⅡ型功能反应的食饵-捕食者模型的定性分析[J].云南民族大学学报(自然科学版),2014,23(3):190-194.
[2]马知恩.种群生态学的数学建模与研究[M].合肥:安徽教育出版社,1996.
[3]刘启宽,张兆强,陈冲.一类具有功能反应的食饵-捕食模型的定性分析[J].重庆理工大学学报(自然科学版),2010(1):118-122.
[4]匡奕群,邱梅青.一类具功能反应的食饵-捕食者模型的定性分析[J].生物数学学报,2008,22(4):629-633.
[5]王育全.一类具HollingⅠ型功能反应的食饵-捕食者模型的极限环及平衡点的全局稳定性[J].怀化学院学报,1989(5):6.
[6]陈柳娟,孙建华.具Holling第Ⅱ类功能性反应的捕食者-食饵系统的定性分析[J].生物数学学报,2003,18(1):33-36.
[7]陈晓鹰,朱婉珍.具有HollingⅡ型功能性反应的捕食者-食饵种群SIS模型定性分析[J].厦门大学学报(自然科学版),2005,44 (1):16-19.
[8]马知恩.常微分方程定性与稳定性方法[M].北京:科学出版社,2001.
[9]堵秀凤.具有收获率的Holling III类功能性反应捕食模型的定性分析[J].哈尔滨理工大学学报,2009,14(6):92-95.
[10]张芷芬.微分方程定性理论[M].北京:科学出版社,1985.
Discussion on the Stability of Singular Point and the Existence of Limit Cycle for A Class of Predator-prey System with Holling II Functional Response
WU Fang
(School of Applied Mathematics,Nanjing University of Finance and Economics,Nanjing,210023,China)
This paper studies the stability of singular point and the existence of limit cycle for a class of predator-prey systems with Holling II functional response,and carries on the qualitative analysis to the system,and gives the discussion results of the stability of singular point and the singularity global stability and the proof of the existence of limit cycle.Finally,numerical examples are put forward to illustrate the effectiveness of the discussion in the article.
Holling II predator-prey system;singular point;stability;limit cycle
O193;Q141
A
1672-2590(2016)03-0018-12
2016-04-04
武芳(1990-),女,山东枣庄人,南京财经大学应用数学学院硕士研究生.
