基于部分函数型线性回归模型的上证指数预测
2016-02-27程丽娟
程丽娟
(岭南师范学院数学与计算科学学院,广东湛江524048)
基于部分函数型线性回归模型的上证指数预测
程丽娟
(岭南师范学院数学与计算科学学院,广东湛江524048)
在金融数据的研究中,经常遇到函数型数据.本文主要建立部分函数型线性回归模型,分析函数型数据在上证指数预测中的应用,根据函数型数据分析的原理及其求解主成分分析的方法,使用Matlab对上证指数进行预测.
部分函数型线性回归模型;函数型数据;预测
本文主要建立部分函数型线性回归模型,根据文献[1]通过把L2空间的函数型数据进行K-L展开,得到部分函数型线性模型中系数的估计量,给出其在上证指数预测中的实证分析,根据函数型数据分析的原理及其求解主成分分析的方法,使用Matlab软件对上证指数进行预测.
1 函数型数据分析
对于定义在概率空间(Ω,B,P)上的实值随机变量Y和(z,X),满足如下的线性关系

则称该模型为部分函数型线性回归模型,其中:z=(z1,z2,…,zp)T为P维随机向量,Ez=0,EzzT存在且有限;{X(t)}∈L2[0,1]为随机过程,均值为零,
E‖X‖2=E<X(t),X(t)>=EX2(t)dt<∞;ε与z,X相互独立,且Eε=0,Varε=σ2;θ(t)∈L2[0,1],且‖θ‖2<∞,β为p维随机向量.
特别地,当β=0时,模型(1)为Y=<θ(t),X(t)>+ε,即为函数型线性模型,当θ=0时,模型(1)为Y=βTz+ε,即为多元线性模型.
记过程X的协方差函数KX(s,t)=Cov(X(S),X(t)),{(λj,φj)}j为协方差算子K(x)(t)=<x (s),KX(s,t)>的特征值和特征函数,即满足K(φj)=λjφj.同样的,记KYX(·)=Cov(Y,X(·)),
KzX(·)=Cov(z,X(·))=(Kz1X(t),…,KzpX(t))T,Kz=Var(z),KzY=Cov(z,Y).
假设已观测了n组样本(Yi,zi,Xi(t))n
i=1,由模型(1)有
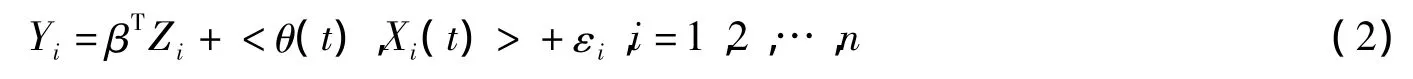
其中εi独立同分布.从而可得KX(s,t)的样本估计值为
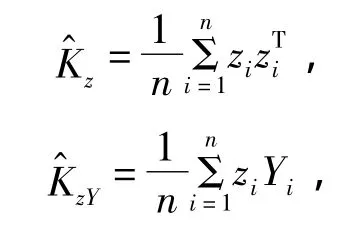
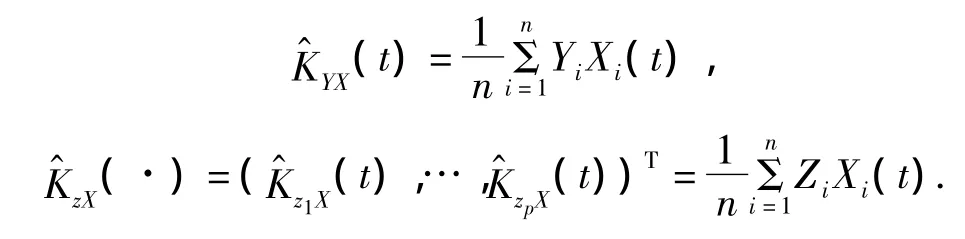
根据文献[2],使用函数型数据主成分分析方法,选择前m个最大特征值对应的主成分将X(t)进行Karhunen一Loève正交展开,使用最小二乘方法得到估计量
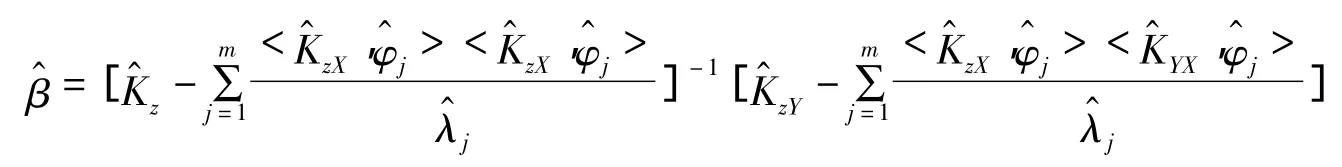
其中:
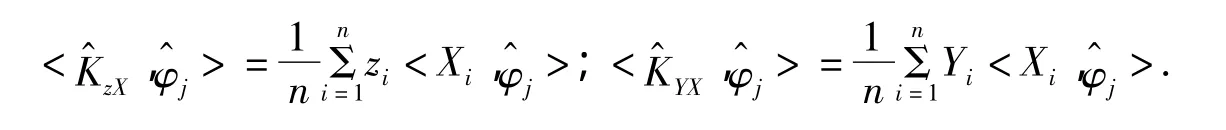
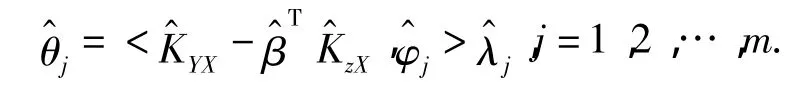
2 实证分析
建立上证指数的函数型数据预测模型,F=μ+Y+ε,其中μ为上证指数的日收益率的均值,Y=βTz +<θ(t),X(t)>+ε为部分函数型线性回归模型,本文选取我国上证指数作为研究对象,其中Y为2015年4月21日至6月8日的日收益率减去其均值后的数据,z~N34(0,I),{X(t)}为2015年4月21日至6月8日的5分钟收益率减去其均值后的数据.这里,z~N34(0,I),则其为随机向量,Ez=0,EzzT存在且有限;{X(t)}∈L2[0,1]为随机过程,均值为零,
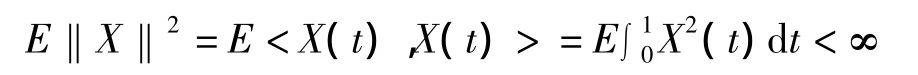
ε与z,X相互独立,且Eε=0,Varε=σ2;θ(t)∈L2[0,1],且‖θ‖2<∞,β为p维随机向量.从而,该模型符合部分函数型线性回归模型的条件,可以进行上证指数预测.
为了避免“隔夜效应”的影响,在进行数据分析时,舍弃每天的第一个数据(即9:35时刻),把每天的5分钟收益率数据视为其对应函数产生的一组样本观测值,使用B样条插值法对这些样本观测值进行拟合,并进行套准和平滑处理,然后根据得到的光滑曲线求出其变化速度曲线,即一阶导数曲线,如下图所示.图1表示的是收益率曲线及其平滑曲线,其中绿线表示的原数据,蓝线表示的是B样条插值法得到的曲线,红线表示对B样条插值法得到的曲线平滑处理后得到的新曲线.图2表示的是B样条插值法得到曲线的一阶导数曲线[3-6].
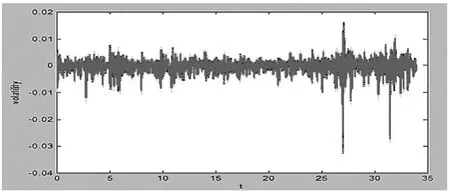
图1 收益率曲线及其平滑曲线
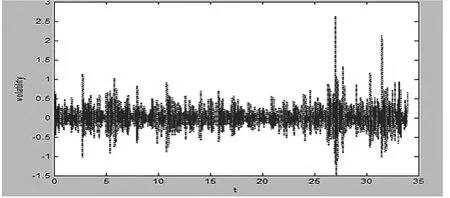
图2 一阶导数曲线
得到平滑函数后,对该收益率函数进行函数型主成分分析,得到主成分权重函数,如下图3所示.
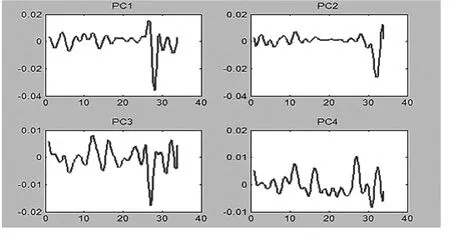
图3 主成分权重函数
得到主成分特征值与贡献率,如下表1所示.

表1 主成分特征值与贡献率
根据表1中的方差贡献率,选取前四个最大特征值对应的主成分将X(t)进行Karhunen一Loève正交展开,使用最小二乘方法得到估计量:

将观测到的真实值、模型估计出的预测值及由两者得到的误差百分比如下表2所示.

表2 真实值与预测值
由表2可以看出,除6月11日误差百分比较大以外,绝大部分的误差百分比都较小.因此说明建立的部分函数型线性回归模型具有很好的准确性.综上知,建立函数型主成分预测模型对我国上证指数收益率进行预测,预测的准确程度较高.
3 结论
本文对部分函数型线性回归模型在上证指数中的应用进行了研究,介绍了函数型数据分析的研究意义,研究了函数型数据的主成分分析方法以及如何使用部分函数型线性回归模型对上证指数进行预测.通过对上证指数收益率进行预测的实证分析,得到建立部分函数型线性回归模型对我国上证指数收益率进行预测,预测的准确程度较高.
[1]Shin H.Partial Functional Linear Regression[J].Journal of Statistical Planning and Inference,2009,139(10):3405-34l8.
[2]Ferraty F,GonzMez-Manteiga W,Martinez-Calvo A,et a1.Presmoothing in Functional Linear Regression[J].Statistica Sinica,2012 (22):69-94.
[3]Ramsay J O.When the data are functions[J].Psychometrika,1982(47):379-396.
[4]Ramsay J O,Hooker G.Functional Data Analysis with R and MATLAB[M].New York:Springer,2009.
[5]Mallor F,Leon T,Gaston M.Changes in power curve shapes as an indicator of fatigue during dynamic contractions[J].Journal of Biomechanics,2010(43):1627-1631.
[6]Berrendero J.R.Principal components for multivariate functional data[J].Computational Statistics and Data Analysis,2011,55(9): 2619-2634.
Prediction for the Shanghai Stock Index Based on the Partial Functional Linear Regression Model
CHENG Li-juan
(School of Mathematics and Computation Science,Lingnan Normal University,Zhanjiang,524048,China)
In the research of financial data,the functional data is often encountered.In this paper,the partial functional linear regression model is established to predict the Shanghai stock index.Based on the principal component analysis theory and calculation method,the Shanghai Composite Index is predicted by Matlab.
partial functional linear regression model;functional data;prediction
F224;F830.91
A
1672-2590(2016)03-0014-04
2016-04-05
岭南师范学院自然科学青年项目(QL1407)
程丽娟(1986-),女,安徽阜阳人,岭南师范学院数学与计算科学学院助教.
