高阶非线性泛涵差分方程的强迫振动性
2016-02-27张锋于祥武徐润
张锋,于祥武,徐润
(1.曲阜师范大学学报编辑部,山东曲阜273165;2.青岛市黄岛区实验中学,山东青岛266400; 3.曲阜师范大学数学科学学院,山东曲阜273165)
高阶非线性泛涵差分方程的强迫振动性
张锋1,于祥武2,徐润3
(1.曲阜师范大学学报编辑部,山东曲阜273165;2.青岛市黄岛区实验中学,山东青岛266400; 3.曲阜师范大学数学科学学院,山东曲阜273165)
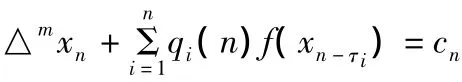
泛函差分方程;非线性;强迫振动项
1 引言
文献[1]究了高阶非线性差分方程
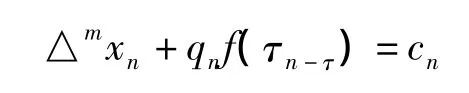
的振动性.其中m≥1,τ≥0是整数.
本文应用[1]中相似的方法,我们研究下面的方程的振动性

其中m≥1且τi≥0是整数,△是向前差分算子,定义为△xn=xn+1-xn,△ixn=△(△i-1xn),其中2≤i≤m,xf(x)>0(x≠0),qi(n)和cn是定义在N0={0,1,2,…}上的实数序列.
设实值序列{xn}是方程(1)的解.如果对每一个n0>0,都存在一个n≥n0,使得xnxn+1≤0,那么这个解{xn}是振动的,否则,方程(1)不具有振动性,如果方程(1)的所有解是振动的,那么方程(1)就是振动的.
很多作者研究了当cn≡0时方程(1)的振动性,见文献[2-18],但是,当cn≠0时,除了[9,10]外很少有人研究.在[9]中,作者假设存在一个实值序列gn,并且gn是变号的,△mgn=cn,当n→∞时,gn→0.
在本文中,我们没有对强迫项限制条件,为了方便,我们定义
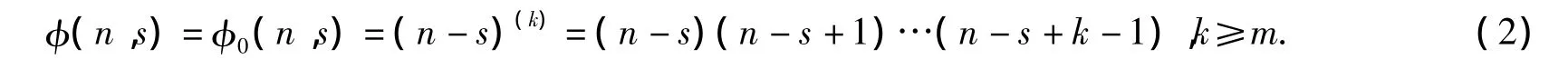
并且
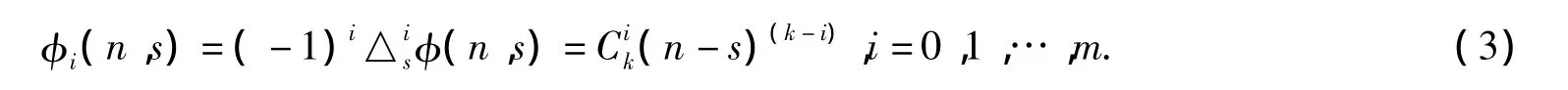
那么我们很容易得到
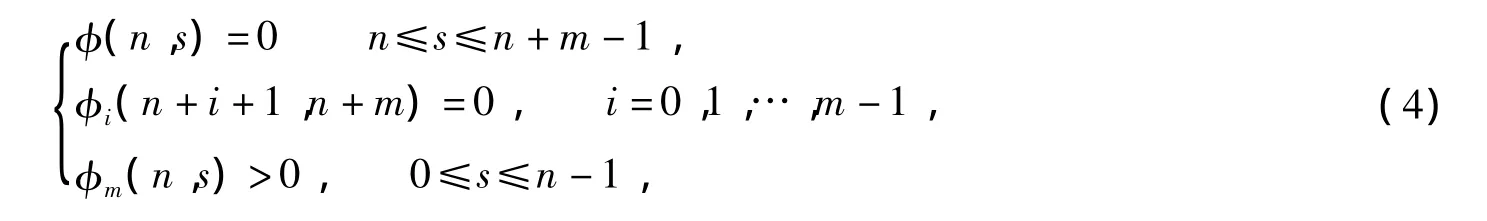
并且
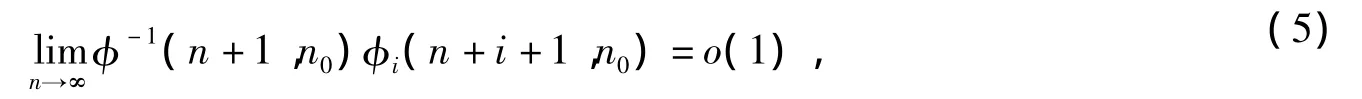
其中n0≥0,i=1,2,…,m.
2 主要结论
引理1[6]令F(x)=ax-bxλ,其中x>0.如果a≥0,b>0并且λ>1,那么F(x)得到它的极大值
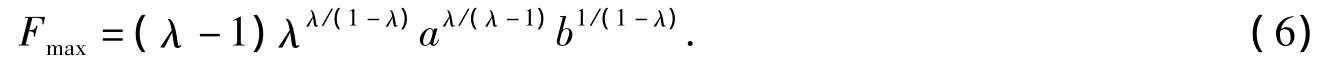
如果a>0,b≥0,0<λ<1,那么F(x)获得它的极小值
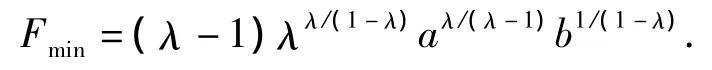
定理1令qi(n)≥0,其中n≥0,i=1,2,…,n.如果
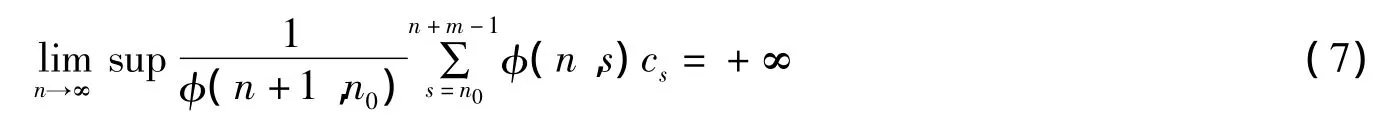
并且
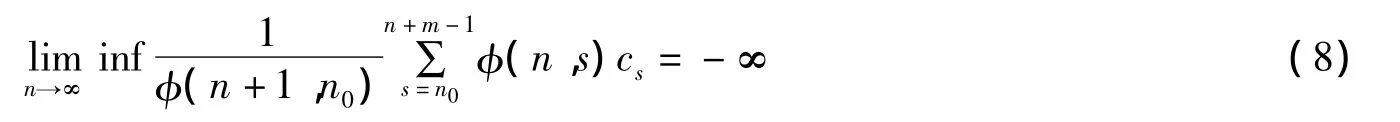
其中n0≥0,那么方程(1)的每一个解都是振动的.
证明令xn是方程(1)的一个非振动解.不失一般性,我们假设xn>0,x(n-τ)>0,其中n≥n0≥0.方程(1)的两边同时乘以φ(n,s),并且对其从n0到n+m-1求和,我们有
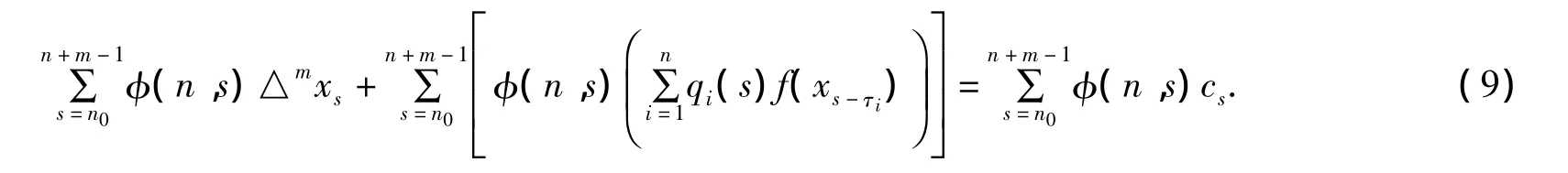
由于
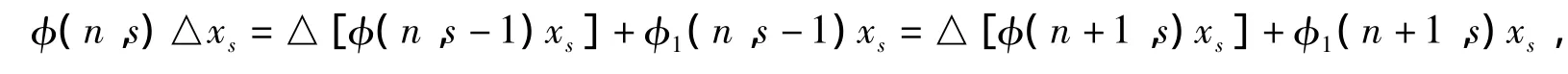
由(2)-(4)我们有
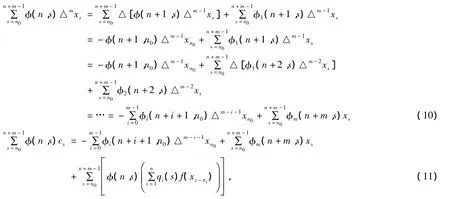
注意到φ(n,s)≥0其中n0≤s≤n-m+1.将(11)代入(9)中,方程两边同时除以φ(n+1,n0),我们得到
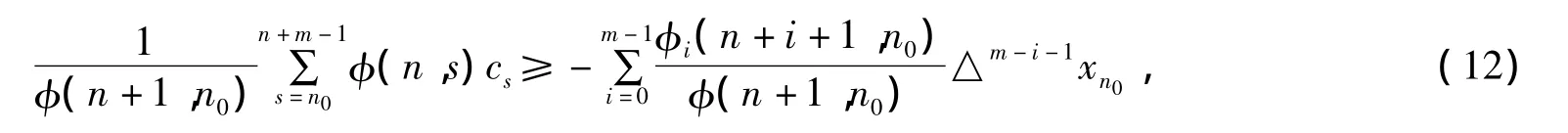
根据条件(5)我们得到上述结论和(8)是相矛盾的.从而定理1得证.
定理2假设qi(n)<0,其中n≥0,存在r>0和λ>1使得|f(x)|≥r|x|λ.如果
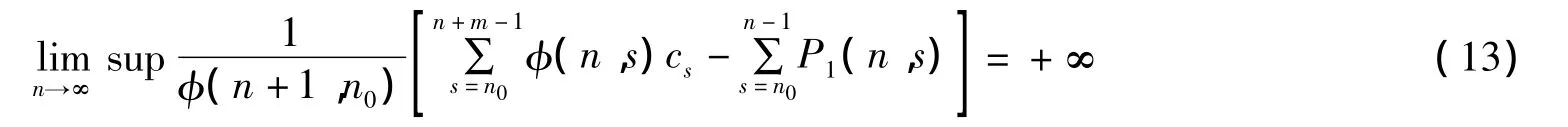
且
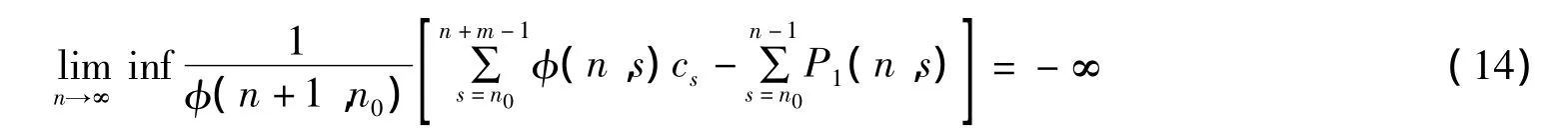
其中n0>0,
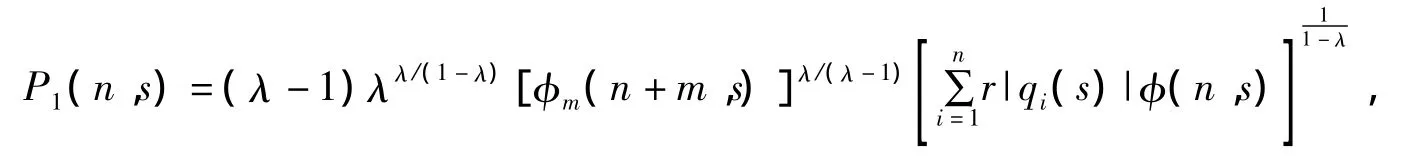
那么方程(1)的每个解在τ=0的情况下满足lim supn→∞|xn|/φ(n+1,n0)<∞时,是振动的.
证明当τ=0时,令xn是满方程(1)的一个非振动性解,满足条件
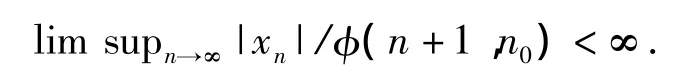
不失一般性,我们假设xn>0且xn≤rφ(n+1,n0).其中n≥n0≥0,r>0是一个常数.方程(1)两边同时乘以φ(n,s),从n0到n+m-1求和.证明过程和定理1类似,我们有
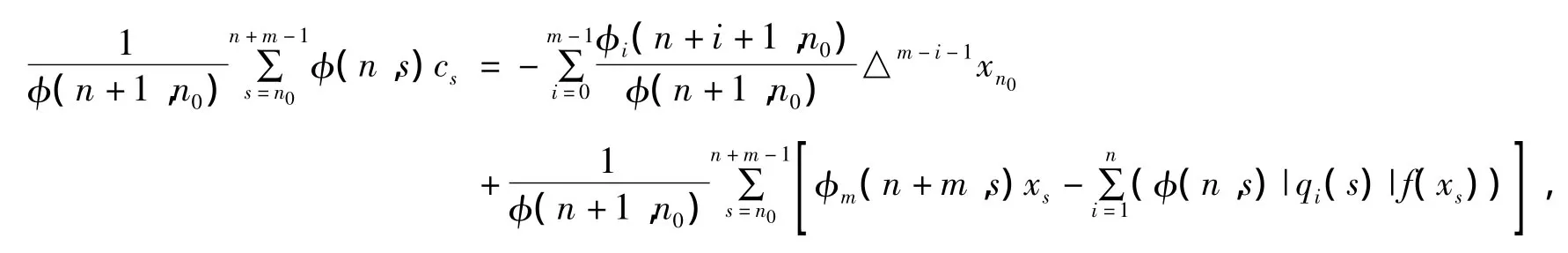
注意到φ(n,s)=0且s=n,n+1,…,n+m-1,我们有
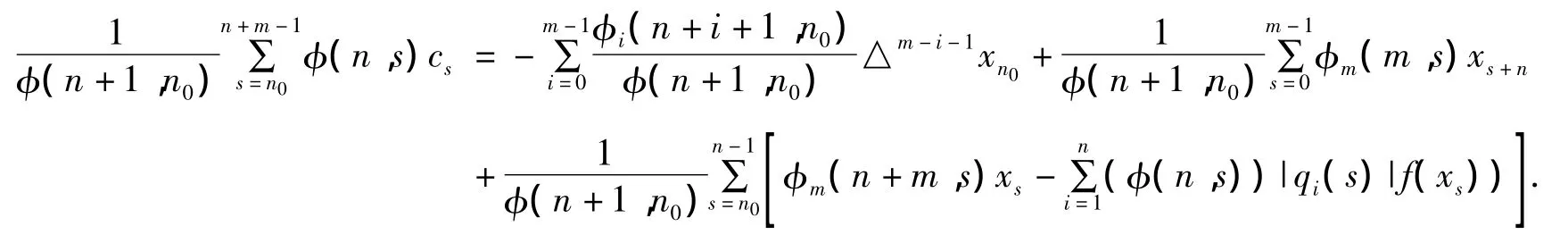
应用关于f(x)的假设,存在一个常数M>0,从而有
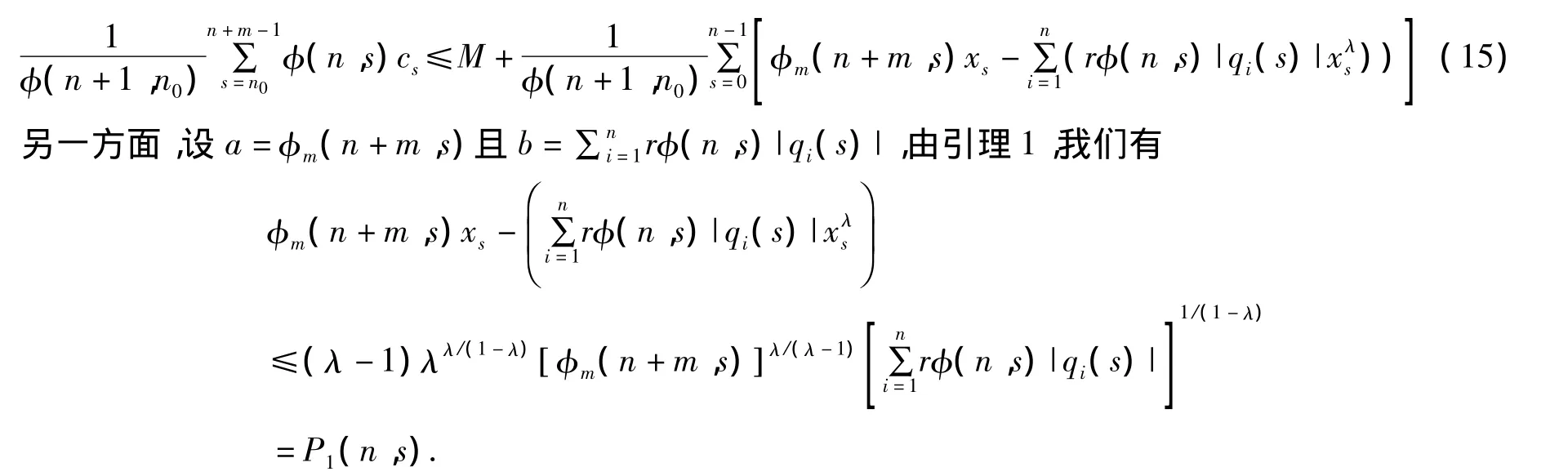
因而,由(15),我们得到
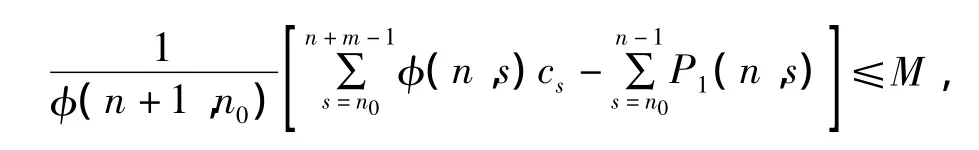
以上的结论和(14)相矛盾,从而定理2得证.
定理3假设存在两个正常数r>0,0<λ<1,使得|f(x)|≤r|x|λ,如果
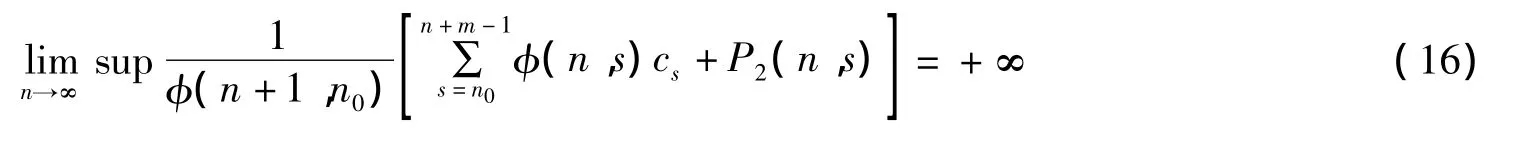
且
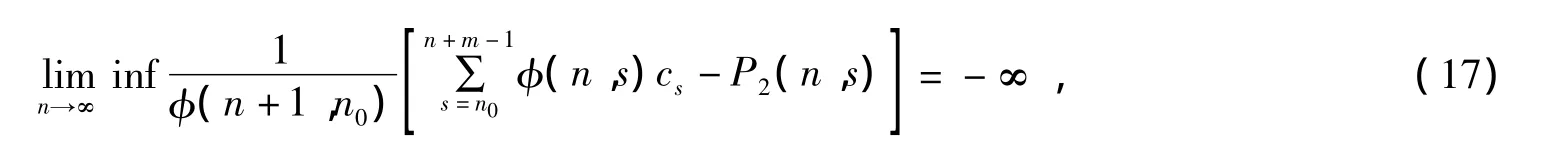
其中n0>0,当
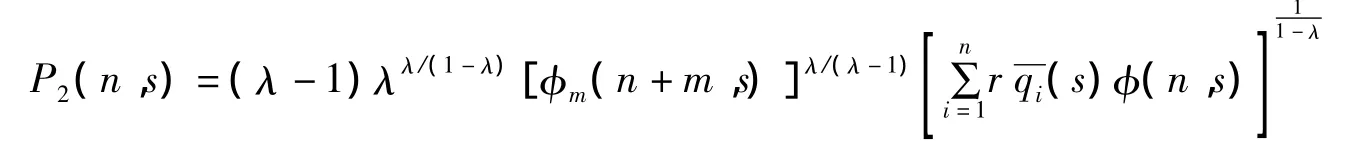
证明当τ=0时,令xn是满方程(1)的一个非振动性解.不失一般性,我们假设xn>0且n≥n0≥0.证明过程和定理2相似,我们得到
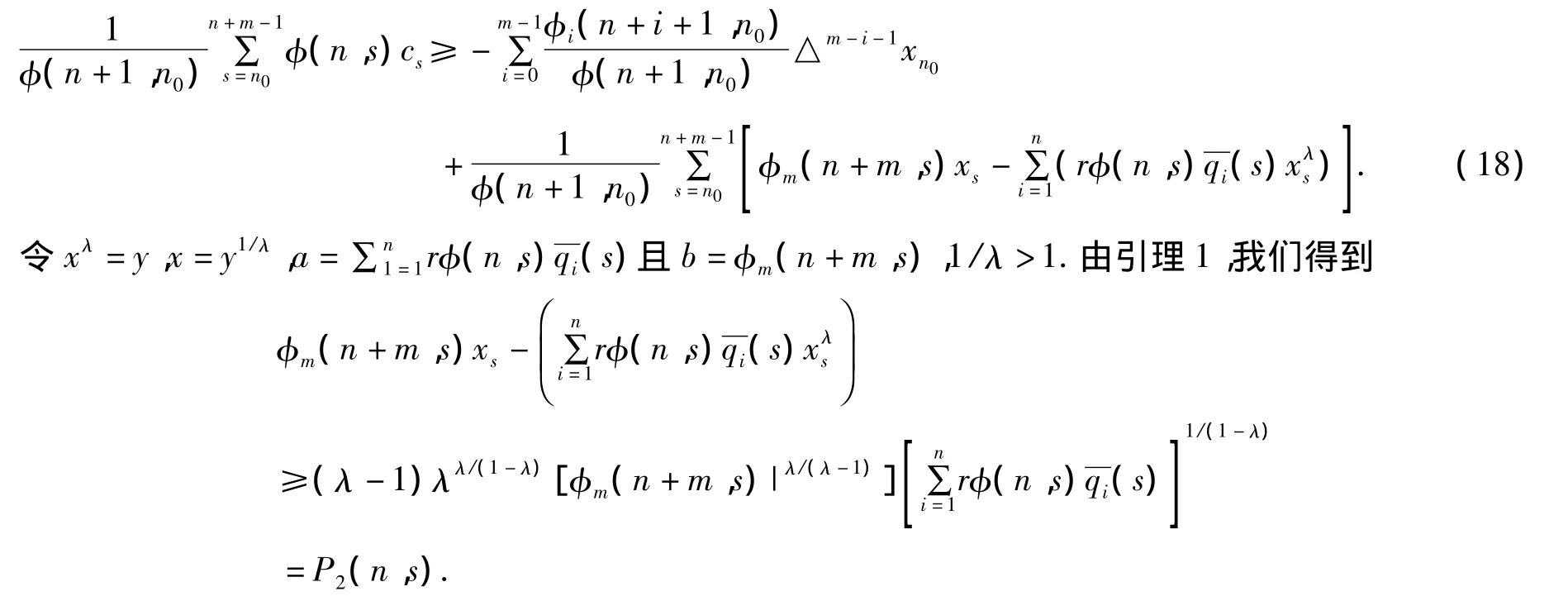
那么,由(18)我们有
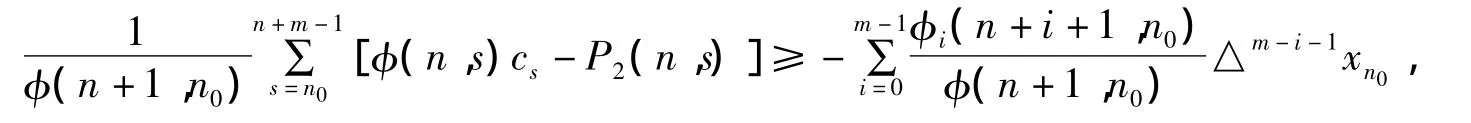
根据(5),上述结论和(17)是相矛盾的,从而定理3得证.为了说明本文的结论,考虑以下几个例子.
例1考虑下面的微分方程
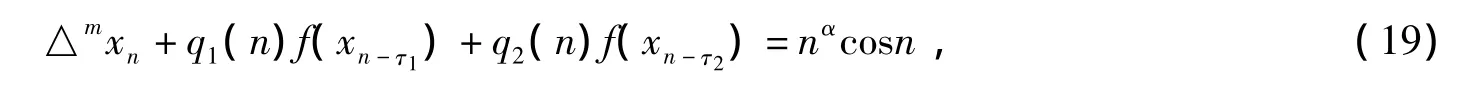
其中m≥1,q1(n),q2(n)≥0且α>0.根据定理1,我们很容易证得方程(19)是振动的,其中α>m-1.
例2考虑下面的微分方程

其中m≥1.α,β是常数.令k=m,那么我们有
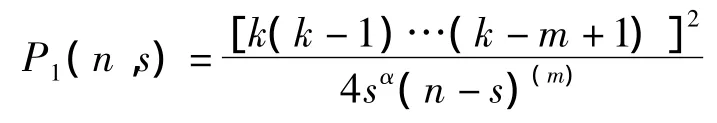
例3考虑下面的微分方程
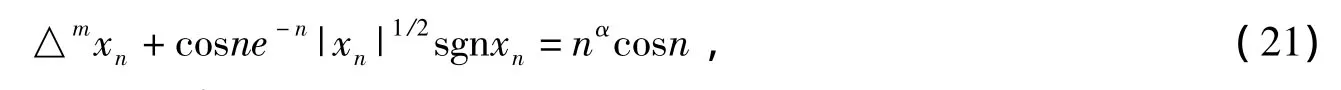
其中m≥1.α≥0是常数.令k=m,那么我们有
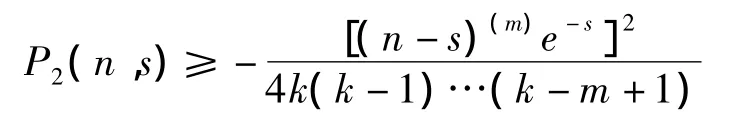
由定理3,我们有方程(21)是振动的,其中α>m-1.
[1]Sun Y G,Saker S H.Forced oscillation of higher order nonlinear difference equations[J].Appl Math.Compt,2007(187):868-872.
[2]Agarwal R P.Difference Equations and Inequalities[M].New York:Dkker,1992.
[3]Agarwal R P,Wong P J Y.Advanced Topics in Difference Equations[M].Dordrecht:Kluwer Academic,1997.
[4]Agarwal R P,Grace S R.Oscillation of higher order nonlinear difference equations of neutral type[J].Appl Math Lett.,1999(12):77-83.
[5]Graef J R.Oscillatory and asymptotic behavior of solutions of nonlinear neutral type difference equations[J].J Aust Math Soc B,1996 (38):163-171.
[6]Hardy G H,Littlewood J E,Polya G.Inequalities[M].Cambridge:Cambridge University Press,1952.
[7]Jiang J.Oscillatory criteria for second-order quasilinear neutral delay difference equations[J].Appl Math Comput,2002(125):287-293.
[8]Jiang J.Oscillatory of second order nonlinear neutral delay difference eqations[J].Appl Math Cpmput,2003(146):791-801.
[9]Parhi N,Tripathy A K.Oscillation of solutions of forced non-linear neutral difference equations of higher order[C].in:Proceedings of the VIII Remanujan Symposium on Recent Developments in Nonlinear Systems[M].New Delhi:Narosa Pub House,2002.
[10]Parhi N,Tripathy A K.Oscillation of a class of nonlinear neutral difference equations of higher order[J].J Math Appl,2003(284): 756-774.
[11]Sun Y G,Saker S H.Oscillation for second-order nonlinear neutral delay difference equations[J].Appl Math Comput,2005(163): 909-918.
[12]Sun Y G.Oscillation and non-oscillation for second-order linear diffference difference equations[J].Appl Math Comput,2005 (170):1095-1103.
[13]Sun Y G.Oscillation and nonoscillation for half-linear second order difference equations[J].Indian J Pure Appl Math,2004(35): 133-142.
[14]Saker S H.New oscillation criteria for second-order nonlinear neutral delay difference equations[J].Appl Math Comput,2003(142): 99-111.
[15]Saker S H,Cheng S S.Oscillation criteria for difference eqautions with damping terms[J].Appl Math Comput,2004(148):421-442.
[16]Saker S H.Oscillation of second-order perturbed nonlinear differnce equations[J].Appl Math Comput,2003(144):305-324.
[17]Szafranski Z.Szamanda B.Oscillation theorems for some nonlinear difference equations[J].Appl Math Comput,1997(83):43-52.
[18]Thandapani E.Oscillation theorems for higher order non-linear difference equations[J].Indian J Pure Appl Math,1994(25):519-524.
Forced Oscillation of Higher-order Nonlinear Functional Difference Equations
ZHANG Feng1,YU Xiang-wu2,XU Run3
(1.Journal Editorial Department,Qufu Normal University,Qufu,273165;
2.Huangdao Experimental Middle School,Qingdao,266400;
3.School of Mathematical Sciences,Qufu Normal University,Qufu,273165,China)
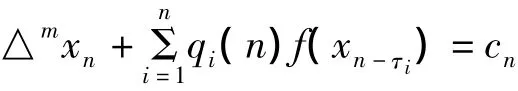
functional difference equations;nonlinear;forced oscillation term
O175.14
A
1672-2590(2016)03-0009-05
2016-04-18
张锋(1966-),男,山东兖州人,曲阜师范大学学报编辑副编审.
