可调磁力减振镗杆动力学模型参数优化

赵　康，罗红波，李　伟

(四川大学 制造科学与工程学院，成都　610065)



可调磁力减振镗杆动力学模型参数优化

赵康，罗红波，李伟

(四川大学 制造科学与工程学院，成都610065)

摘要：针对内置式动力减振镗杆因阻尼液在振动情况下易泄露和橡胶圈易疲劳失效而降低减振性能的问题，提出一种新型的可调磁力减振镗杆。通过建立可调磁力减振镗杆的动力学模型，得到一个二自由度的系统，在建立动力学模型运动微分方程后，采用效率较高的分支定界搜索法来优化函数，得到相对振幅的理论最小值和优化参数。由于减振镗杆工作在一个较宽的频域范围，还需利用幅频响应曲线在外界激振力频率变化范围内平均值最大值取得最小来修正优化参数。最后通过与同尺寸的内置式单减振镗杆在频域内的幅频特性曲线对比，前者更小的振幅说明可调磁力减振镗杆具有更好的减振性能。

关键词：磁力减振镗杆；动力学模型；参数优化；性能分析

0引言

镗削加工大深孔时，为了减小镗杆的颤振，提高镗杆的加工精度，目前已有很多内置式动力单减振、双减振镗杆的研究，均有一定的减振效果[1-2]。但是这类内置阻尼液和弹性元件橡胶圈减振镗杆，因阻尼液在振动情况下易泄露,设计阻尼值易被破坏和弹性橡胶圈易疲劳老化易被腐蚀等缺陷，导致减振的长久性和稳定性得不到保证，所以这里提出采用利用电磁场提供的刚度阻尼替代橡胶圈和阻尼液，从而克服这类内置式减振镗杆的不足[3]。

磁力减振镗杆由两部分组成，一是机械系统，二是控制系统。磁力减振镗杆的机械结构主要由镗杆体、刀头和减振系统组成。如磁力减振镗杆的结构示意图1所示，磁力减振镗杆的减振系统是由一个减振块4和减振块两端的铁芯7、电磁铁6、保护橡胶圈8和限位橡胶圈5组成。其中保护橡胶圈在镗杆工作过程中不起支撑作用，而是由电磁铁产生的磁场对减振块产生刚度阻尼作用，橡胶圈只是在电磁铁未通电即镗杆停止工作时或电磁铁工作产生异常情况下对减振块起保护作用；为了简化镗杆结构和控制，减振块轴向运动没有加以电磁铁控制，因为轴向振动对镗削加工精度影响小，轴向振幅也不大，因此用限位橡胶圈限制减振块的轴向位移是可行的。镗杆镗削加工时，减振块铁芯受到电磁铁的电磁吸力，通过电磁铁控制系统使减振块悬浮在平衡位置，代替橡胶圈支撑减振块，同时电磁场对减振块的电磁吸力作用可以等效为橡胶圈和阻尼液的刚度阻尼作用。只要结构参数和控制参数设置得当，就可以使镗杆具有很好的减振性能。

1.刀头 2.堵 3.保护橡胶圈 4.减振块 5.限位橡胶圈 6.电磁铁 7.减振块铁芯 8.垫片 9.镗杆体

图1磁力减振镗杆结构示意图

1可调磁力减振镗杆的动力学模型

选取磁力减振镗杆的刀尖作为研究对象，镗杆杆体的质量等效为一质量块，用m1表示，减振块用等效质量块m2表示，研究点刀尖的刚度等效为一弹簧，刚度系数为k1，磁场对减振块产生刚度、阻尼分别等效为k2、c2。这样就可以简化出磁力减振镗杆的动力学模型，如图2所示。

图2　磁力减振镗杆等效动力学模型

由图2可知，磁力减振镗杆由两个系统组成，主系统m1、k1和减振块系统m2、k2组成。主系统在外界激振力的作用下就会产生振动，而减振块系统由于动力作用可以减小或消除振动。这是一个二自由度的系统，其自由振动是由两种不同频率的简谐运动复合而成。这两个频率只取决于系统的弹性和惯性特性。系统在受到外界激振做强迫振动时，如果激振力的频率与系统的固有频率接近时就会发生强烈的振动。

当质量块上受到外界激励时，系统就不是二自由度系统的自由振动了。镗杆在镗削加工时，刀尖受到切削力的作用，此时系统是一个受迫振动状态。假设作用在质量块m1上的力为F1sin(wt),其中F1不为零，则图2所示的动力学模型运动微分方程可写为：

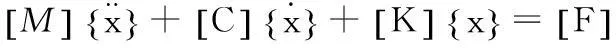
(1)

其中

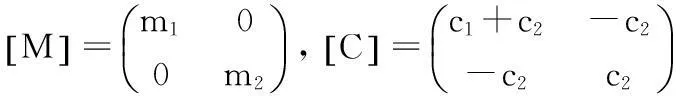
由稳态振动叠加而成，系统的稳态响应与激振力频率相同，但由于系统阻尼的存在，使得响应和激振之间存在相位角差，设方程(1)的解为：

(2)

由式(1)、(2)可解得未知数B1C、B1S、B2C、B2S，因此系统的振动方程可写为：

(3)

式中：

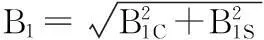
φ1=tan-1-B1C/B1S；φ2=tan-1-B2C/B2S

由式(3)可知，系统的响应不仅取决于外界激振力的大小，激振力的频率对系统的响应也有很大的影响。当激振频率与任一固有频率相接近时，振幅将趋近于无穷大，即产生共振。

减振镗杆在镗削加工时，最需要关注的是镗杆刀尖的振幅值，此振动振幅值越小，减振镗杆的减振性能越好。因此要求解主质量的振幅x1。由式(3)可知，只要求得B1即可知道主系统的振幅。

令：

α=ω1/ω2(α为质量块2的固有频率与质量块1的固有频率之比)

μ=ω1/ω2(μ为质量块2与质量块1的质量之比)

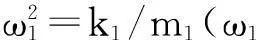
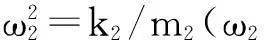
ζ1=c1/2m1ω1(c1为质量块1受到的阻尼)

ζ2=c2/2m2ω1(c2为质量块2受到的阻尼)

λ=ω/ω1(λ为外界激振力频率与质量块1固有频率之比)

B0=F1/K1(B0为外界激振力幅值与质量块1刚度之比，称为静位移)

并作如下代换[4]：

g=2λζ2

h=α2-λ2

p=λ4+(-1-α2-4ζ1ζ2-μα2)λ2+α2

q=(-2ζ2-2ζ1-2μζ2)λ3+(2ζ2+2α2ζ1)λ

根据运动微分方程(1)，可得减振镗杆主系统的相对幅值为：

(4)

从上式可以看出，相对幅值S的含义是减振镗杆刀尖在受到外界激振力时产生的振动幅值与刀尖受到与外界激振力幅值相等的静力作用下产生的静变形的比值。相对幅值可以表征刀尖在外界激振力的作用下振动幅值的大小，对于减振镗杆而言，总是希望此值越小越好。要得到减振性能好的镗杆，需要使减振镗杆主系统的相对幅值S在满足实际约束条件时取得最小值。由减振镗杆主系统的相对幅值S表达式(4)可知，S与α、μ、ζ1、ζ2、λ这五个变量有关，求解S的最大值最小，即是求解这五个变量在一约束条件下的极大值问题。

2磁力减振镗杆动力学模型的参数优化

磁力减振镗杆系统动力学模型的参数优化问题可描述为：在给定变量α、μ、ζ1、ζ2的范围内进行寻优，使得目标函数即减振镗杆主质量的最大相对幅值最小。将其描述为数学模型为：

目标变量：α、μ、ζ1、ζ2；

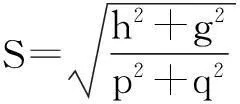
优化目标：优化函数的最大值最小；

约束条件：0.6≤α≤1.5，0.025≤μ≤0.5，0.1≤ζ1≤1.0，0.1≤ζ2≤1.0。

约束条件是根据减振镗杆的实际条件进行设置的，如果不加以约束，得到的优化值可能是最优的，但是如果按照这样的优化参数值进行镗杆设计很可能不符合实际，例如得到的参数值为负值，或者得到的参数值使减振镗杆无法装配等。

从此优化数学模型可以看出，优化函数S不是显示表达，因此传统的拉格朗日乘数法、拟牛顿法等求解极值方法无法进行求解。针对此二自由度系统的优化采用效率比较高的分支定界搜索法(branch and bound)[5]来优化函数。数学软件Maple工具箱中有十分成熟的分支定界算法优化工具，可以自用它进行优化求解。在Maple中编写好程序后，可以很快计算出优化参数。其中一组优化参数为：

α=0.79,μ=0.20,ζ1=0.09,ζ2=0.20

(5)

此时幅频响应曲线如图3所示，由图3可知，当时ζ2=0.707，最大相对幅值为2.311。由于减振镗杆的工作是在一个比较宽的频域范围，所以不能以某一频率点的减振性能来代替频率带内的减振性能。因此对于此优化参数进行宽频范围内的减振评估，通常利用幅频响应曲线在外界激振力频率变化范围内平均值最大值取得最小来修正优化参数。连续函数的平均值公式为：

(6)

图3　优化参数时的幅频响应曲线

令α、μ为定值，将ζ1、ζ2作为变量进行微调修正。从图3可以看出系统的幅在λ=0.1~2的时候变化比较大，所以计算平均值的积分范围设为(0.1,2)。将α=0.79、μ=0.20、ζ1=0.09、ζ2=0.20代入相对幅值函数(4)中，则优化目标函数为：

(7)

在Maple[6]中编写好优化程序计算得到修正后的参数为：

α=0.79,μ=0.20,ζ1=0.09,ζ2=0.23

(8)

由此可得到修正后的幅频响应曲线，将减振镗杆的理论最优曲线和修正曲线画在同一坐标系下，如图4所示。

由图4可知，当时λ=0.73，修正幅频响应曲线的最大相对幅值为2.327。经计算得到优化幅频响应曲线和修正幅频响应曲线的平均值和最大值如表1所示。

图4　修正幅频响应曲线1与理论最优幅频响应曲线2

α、μ、ζ1、ζ2SSmax修正曲线0.79,0.20,0.09,0.230.9434172.327理论最优曲线0.79,0.20,0.091,0.200.9439672.311

由表1可以看出优化幅频响应曲线和修正幅频响应曲线的平均值和最大值相差都不大，但是从图4可知，当λ=1优化幅频响应曲线相对幅值比修正幅频响应曲线相对幅值大，而λ=1正是引起共振的频率点，应该使此时的相对幅值尽可能小。因此，最终减振镗杆的参数磁力减振镗杆的优化参数为修正幅频响应曲线对应的参数α=0.79,μ=0.20,ζ1=0.09,ζ2=0.23。

3可调磁力减振镗杆减振性能分析

采用Ansoft Maxwell和Ansys Workbench相结合的方法可以对磁力减振镗杆进行了磁-结构耦合进行仿真，分析镗杆静力学、动力学方面的性能。这里我们主要根据最终的优化参数在Ansys中采用模态叠加法(Mode Superposition)[6]对磁力减振镗杆的作谐响应分析。

刀尖各方向振幅对加工精度和表面质量的影响，径向最大，切向次之，而轴向几乎可以忽略不计，因此径向和切向这振幅是主要考虑的。磁力减振镗杆刀尖径向(X轴)和切向(Y轴)幅频响应曲线如图5、图6所示。同时引用内置式单减振镗杆[7]的径向、切向幅频响应曲线如图7、图8所示。此内置式单减振镗杆所用减振系统刚度为0.68×106N/m，阻尼为1190N·s/m。

从图5、图6可以看到，磁力减振镗杆刀尖径向振幅最大值为2.26e-3mm，切向最大振幅值为1.35e-2mm，最大振幅取值都在第二阶固有频率22.14Hz附近。相对于采用橡胶圈和阻尼液提供减振系统刚度阻尼的某一内置式单减振镗杆刀尖径向振幅最大值7.69e-2mm、切向最大振幅值0.447mm来说，磁力减振镗杆的径向和切向最大振幅都有很大的降低，减振性能比较显著。

减振块振幅会在加工过程中变化，假设某个时刻控制系统调节流过电磁铁线圈的电流为0.8A，经过求解，可得到磁力减振镗杆刀尖径向(X轴)幅频响应曲线和切向(Y轴)幅频响应曲线如图9、图10所示。从幅频响应曲线可以看出在径向最大振幅为5.09e-3mm，切向最大振幅为2.81e-2mm，可见磁力减振镗杆在控制调节过程中刀尖振幅也不大，拥有良好的减振性能。

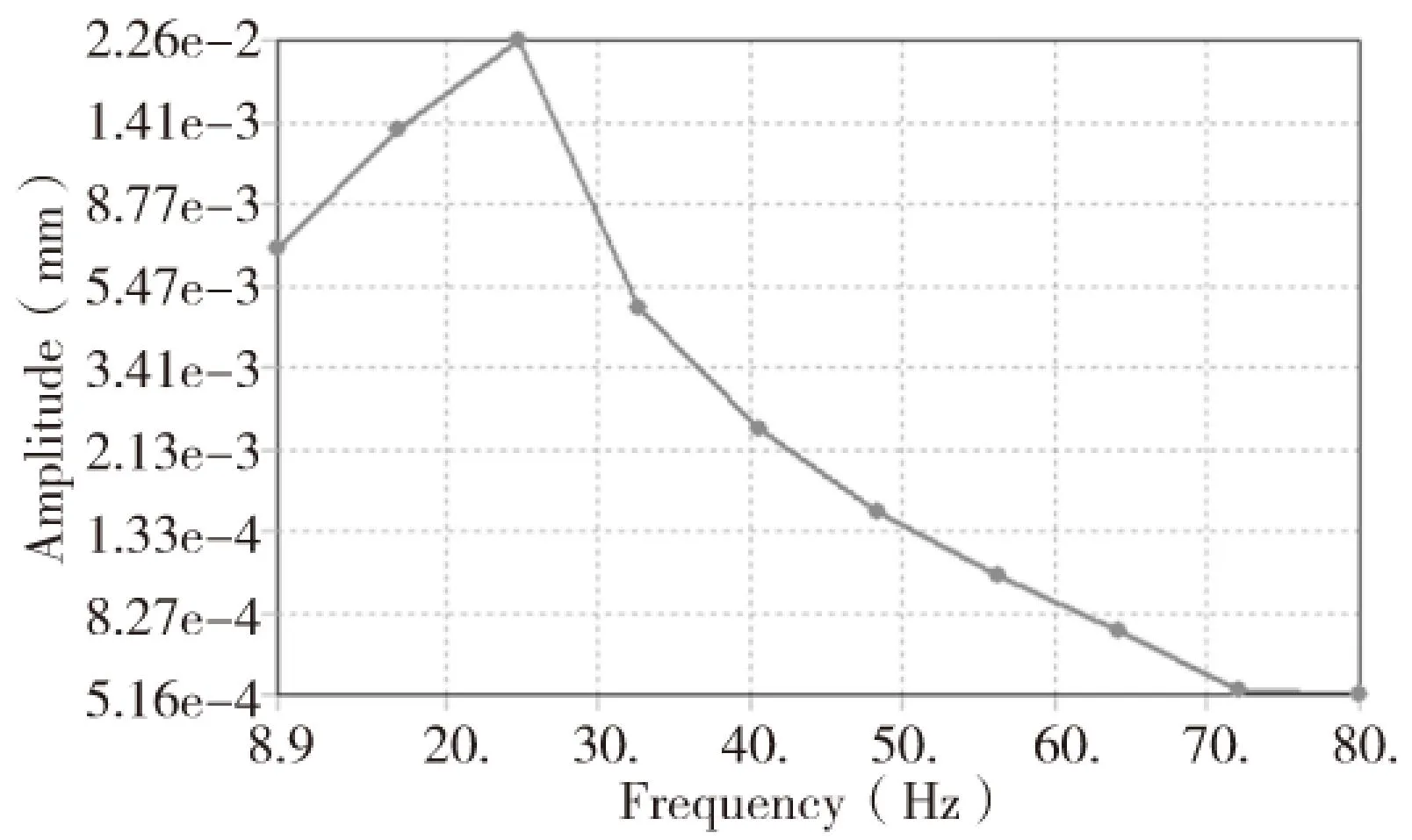
图5　磁力减振镗杆径向(X轴)幅频响应曲线

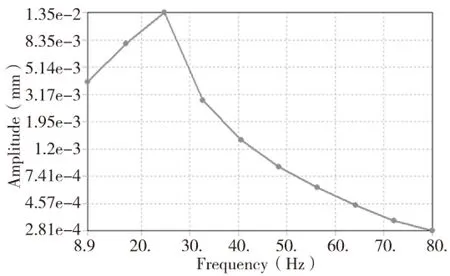
图6　磁力减振镗杆切向(Y轴)幅频响应曲线

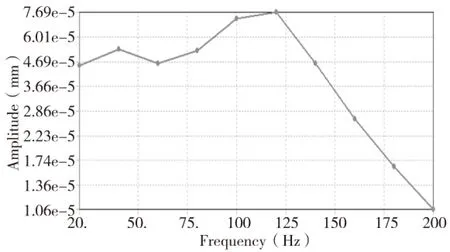
图7　某内置式单减振镗杆径向幅频响应曲线

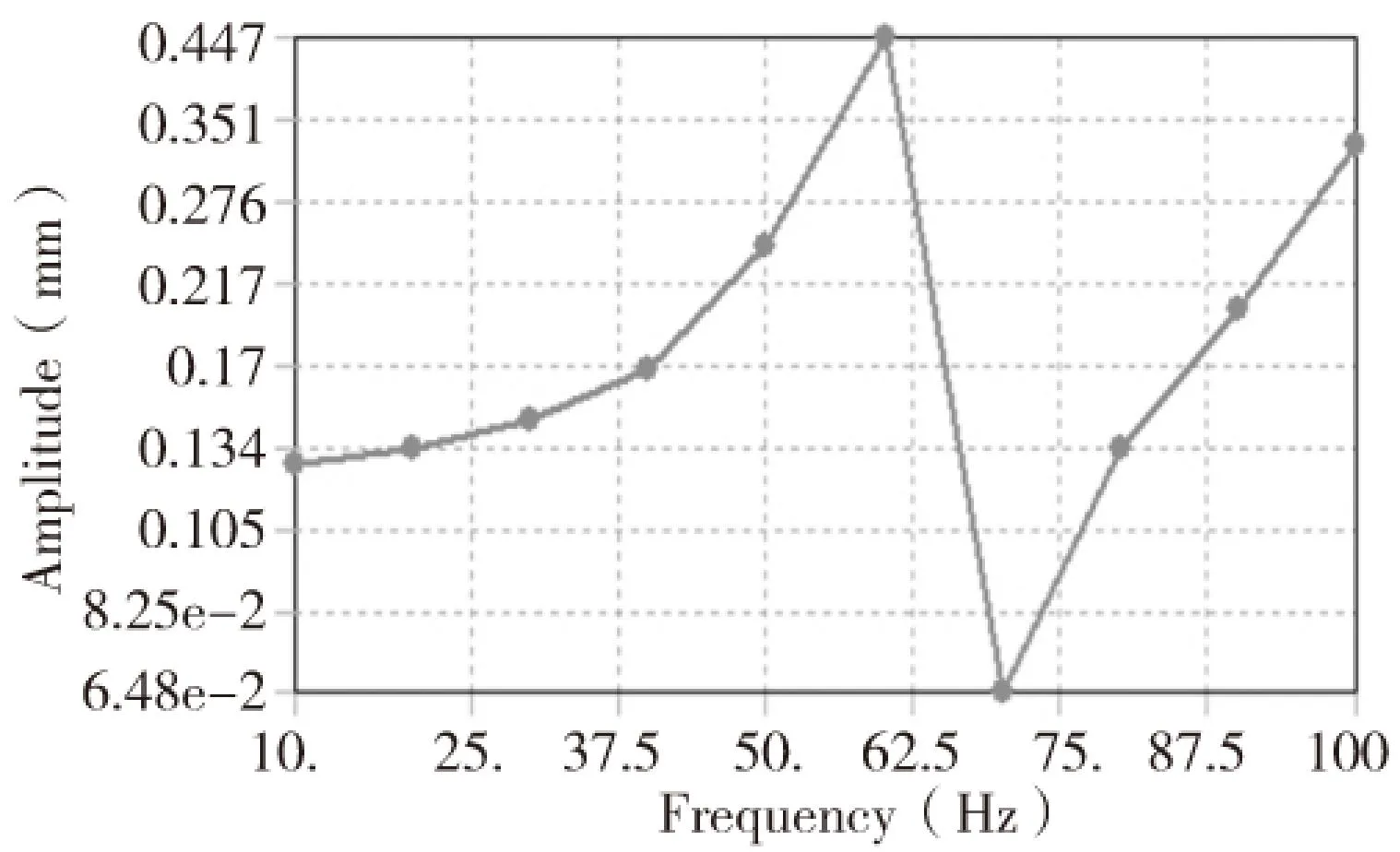
图8　某内置式单减振镗杆切向幅频响应曲线

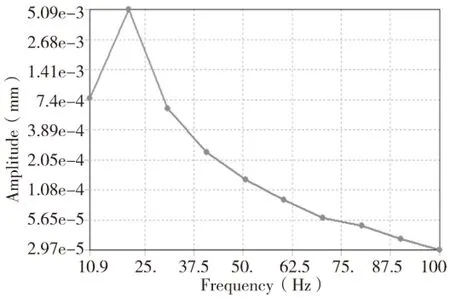
图9　磁力减振镗杆径向(X轴)幅频响应曲线(0.8A)

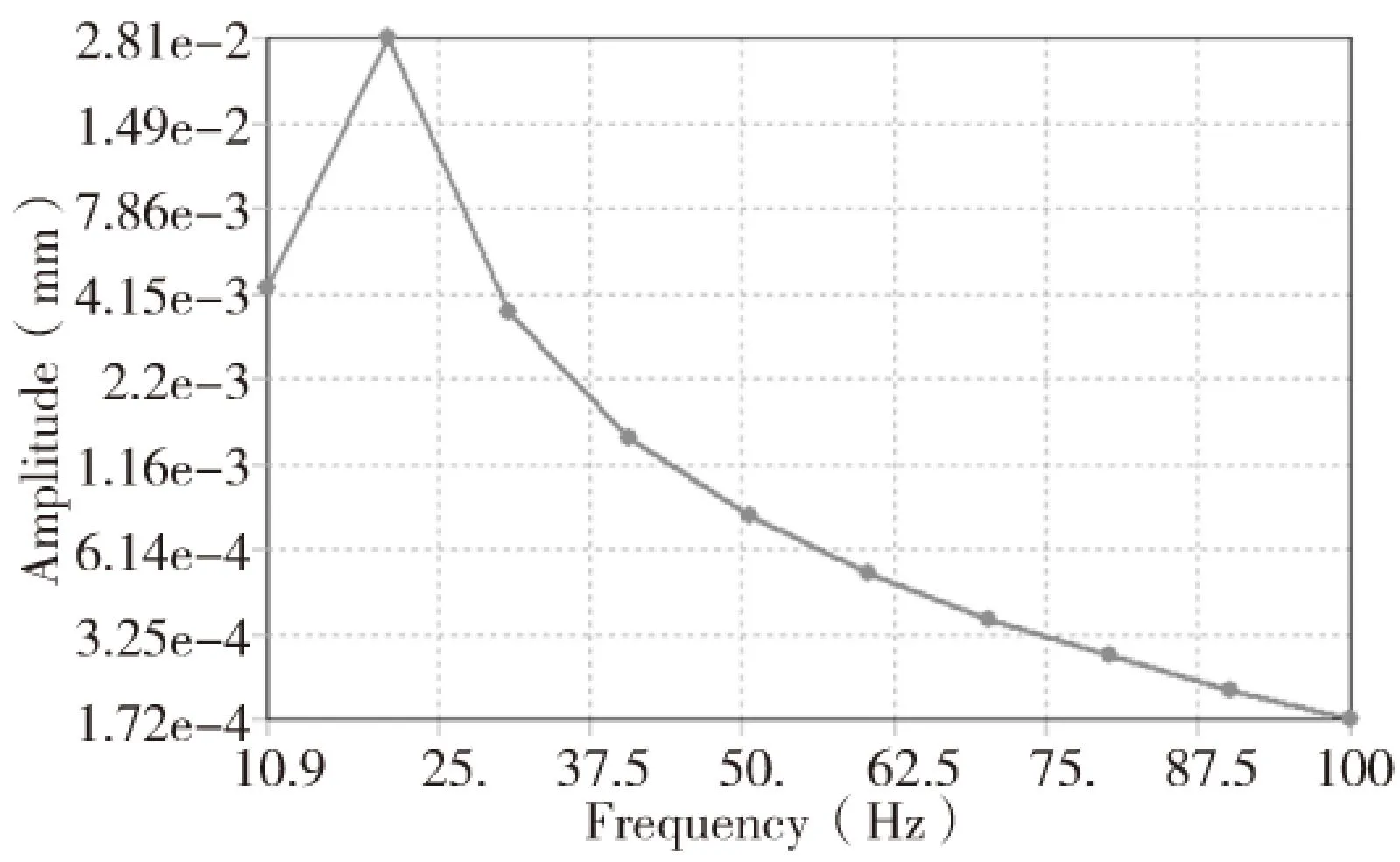
图10　磁力减振镗杆切向(Y轴)幅频响应曲线(0.8A)

4结束语

通过建立可调磁力减振镗杆的一个二自由度的动力学模型，抽象出刀尖的相对振幅函数表达式，利用分支定界优化方法算得相对振幅最大值最小时的优化参数，α=0.79,μ=0.20,ζ1=0.09,ζ2=0.23，并且该组优化参数校验可以看到相对振幅最小。在Ansys中对可调磁力减振镗杆的谐响应分析，磁力减振镗杆刀尖径向振幅最大值为2.26e-3mm，切向最大振幅值为1.35e-2mm，相对于采用橡胶圈和阻尼液提供减振系统刚度阻尼的某一内置式单减振镗杆刀尖径向振幅最大值7.69e-2mm、切向最大振幅值0.447mm来说，磁力减振镗杆的径向和切向最大振幅都有很大的降低，减振性能比较显著，说明可调磁力减振镗杆在解决内置式动力镗杆中橡胶圈和阻尼液自身材料存在的缺陷而影响镗杆的减振性能的同时，也大大提高镗杆的减振性能，也为镗杆减振的继续深入研究提供一定参考。

[参考文献]

[1] 罗红波, 李伟, 唐才学. 内置式双减振镗杆动力学模型参数优化 [J]. 四川大学学报:工程科学版, 2012,44(5):207-212.

[2] Lee D,HwangHuiyun,Kim J.Design and manufac-ture of a carbon fiber epoxy rotating boring bar[J].Composite Structures,2003,60(1):115-124.

[3] 陈可，李伟，罗红波.基于Matlab的可调磁力减振镗杆控制系统参数优化[J].组合机床与自动化加工技术，2014(3):101-103.

[4] 李红梅. 基于有限元分析的内置式减振镗杆研究[D].成都:四川大学,2011.

[5] 杨夷梅, 杨玉军. 分支定界算法优化研究 [J]. 中国科技信息, 2008(21):42-43.

[6] Lee T, Schmitke C. Advanced Engineering calculation-ns and simulations[R]. Maple Soft product Applicat-ion, 2009:28-32.

[7] 唐才学. 数控车床内置式双减振镗杆研究 [D].成都:四川大学, 2010.

(编辑李秀敏)本刊欢迎订阅!

欢迎在线投稿!

欢迎刊登广告!

http:∥www.zhjcz.com.cn

parameters Optimization of Controllable Magnetic Damping Boring Bar’s Kinetic Model

ZHAO Kang,LUO Hong-bo,LI Wei

(School of Manufacturing Science and Engineering,Sichuan University,Chengdu 610065,China)

Abstract：For the vibration damping performance of built-in dynamic vibration boring bar wo-uld bereduced while damping liquid is easy to leak in the condition of vibration and the rubber ring is easy to fatigue failure, thecontrollable magnetic damping boring bar was co-nsidered. Through the establishment of kinetic model of controllable magnetic damping bori-ng bar, the two degree of freedom system can be concluded. After the differential equation-ns of motion of kinetic model is established, using branch and bound algorithm which hav-e high efficiency to optimize the function, and then the theoretical minimal value of the re-lative amplitude and the parameter optimizations were got. Because the damping boring bar- work in a wide frequency range, using the maximum of the average value of the amplitu-de frequency response curve in the scope of external excitation force frequency achieve min-imum to modify the parameters optimizations. Then compared the amplitude frequency char-acteristic curve with the built-in single damping boring bar with the same size in the frequen-cy domain, it can be seen that amplitude of the former is smaller ,which illuminates that thecontrollable magnetic damping boring bar has better damping performance.

Key words：magnetic damping boring bar; kinetic model; parameters optimization;performance analysis

中图分类号：TH166;TG659

文献标识码：A

作者简介：赵康(1991—)，男，四川遂宁人，四川大学硕士研究生，研究方向为计算机数控技术及工业设备自动化，(E-mail)foreverZK@yeah.net。

收稿日期：2015-02-10

文章编号：1001-2265(2016)01-0094-04

DOI:10.13462/j.cnki.mmtamt.2016.01.026