一种弹性折叠梁的刚度建模分析*

刘　斌，张彦斐，宫金良

(山东理工大学 机械工程学院，山东 淄博　255049)



一种弹性折叠梁的刚度建模分析*

刘斌，张彦斐，宫金良

(山东理工大学 机械工程学院，山东 淄博255049)

摘要：刚度对微动平台的驱动行程具有极大影响，为了有效提高微动平台的行程范围，提出一种弹性折叠梁代替传统的弹性薄板结构。首先将整体结构划分为横梁和竖直梁两种不同单元，并建立相应的刚度方程，然后和各个节点的力平衡方程相结合，得到单侧结构的刚度方程。再根据结构的对称性，建立另一侧结构的刚度方程。最后根据两侧结构的变形协调关系推导出弹性折叠梁的整体刚度矩阵。最后给出了数值算例，表明刚度建模方法在分析驱动载荷方向的变形时候偏差很小，但是其他方向的牵连变形精确度较低，因此应以ANSYS分析结果为准。

关键词：微动平台；弹性折叠梁；刚度

0引言

驱动行程是微动机构的重要设计评价指标，而各个环节的刚度都在一定程度上影响着驱动行程[1-3]。很多学者在这一领域进行了深入研究，如Gosselin[4]借助雅可比矩阵，建立了仅考虑主动关节弹性的刚度模型，提出了并联机构的刚度映射矩阵。以此为基础，学者们考虑了机架及支链组件变形，对并联机构进行了静刚度分析[5-7]。在分析的基础上，很多学者研制了微动平台样机[8-9]。随着应用领域的逐步扩大，实际应用的微动平台对行程提出了更高的要求，因此如何对铰链参数优化设计，创造新型柔性铰链成为研究的热点。

1弹性折叠梁的机构描述

弹性折叠梁基于弹性薄板的微小形变，通过多层设计实现微小形变的累计达到大位移输出的目的，既保证了运动精度，又降低了系统刚度，可以作为微动平台设计的重要结构单元，其平面结构如图1所示。弹性折叠梁由两条关于y轴对称的支链组成，z轴方向的柔性梁厚度为b，折叠梁的各处壁厚均相等。

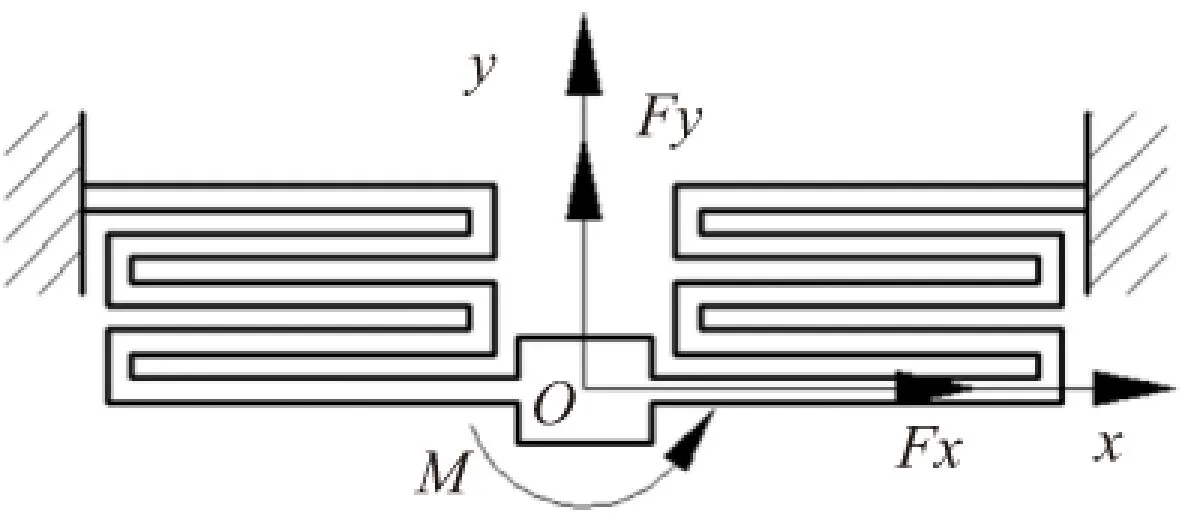
图1　折叠梁

由于结构的对称性，因此可以取弹性折叠梁的半结构进行分析，具体结构参数如图2所示。同时为便于分析，标志了结构关键点进行单元划分，主要包括横梁和竖直梁两类，其中点i与点i+1 (i=1,3,5,7)之间为横梁，点i与点i+2 (i=2,3,6,7)之间为竖直梁，如图3和图4所示。

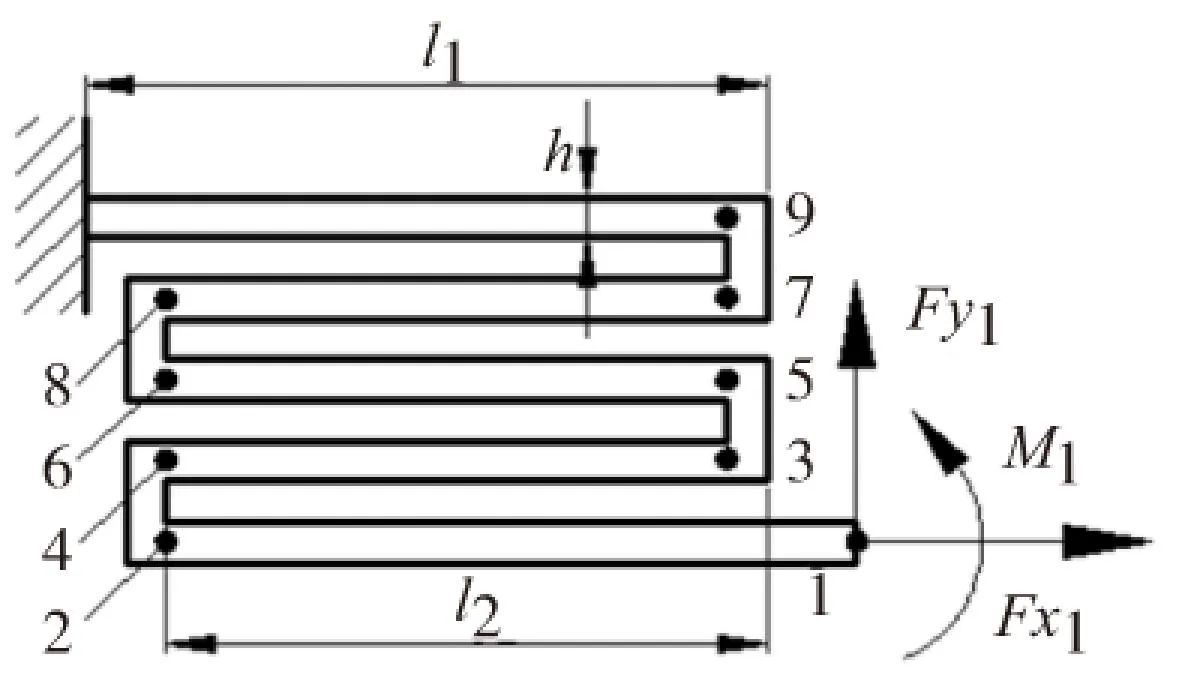
图2　折叠梁左支链

图3　横梁单元

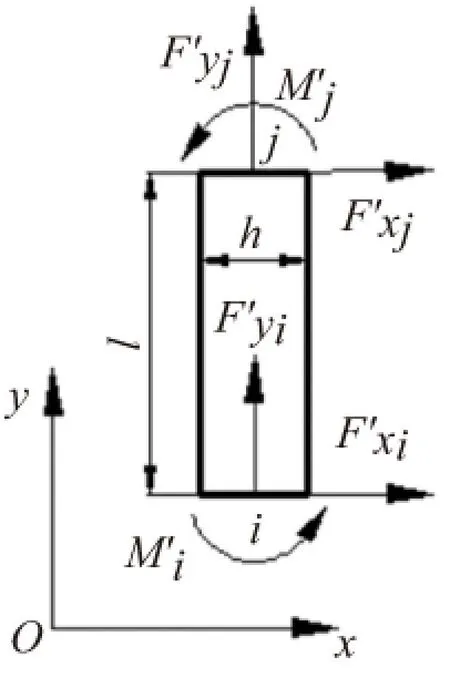
图4　竖直梁单元

2弹性折叠梁支链的柔度模型

2.1支链中各柔性梁单元刚度方程

图3中点i与点i+1之间横梁单元的刚度方程可以表示为：

(1)

式中，

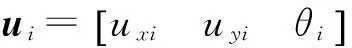
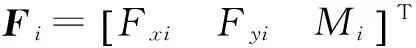
进一步得到：

(2)

图4中竖直梁单元的刚度方程可由横梁的单元刚度方程通过坐标变换得到，坐标变换矩阵为：

根据坐标变换矩阵及横梁的单元刚度方程，点i与点i+2 (i=2,3,6,7)之间竖直梁的单元刚度方程为：

(i=2,3,6,7)

(3)

式中，

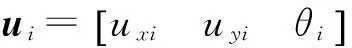
进一步得到：

(4)

图2中点9处悬臂梁的刚度方程为:

F9=T-1kLTu9=k9u9

(5)

2.2支链中的力平衡方程

点i与点i+1之间横梁的力平衡方程可表示为：

Fi=-(li,i+1A1+E)Fi+1(i=1,3,5,7)

(6)

式中，li,i+1为点i与点i+1之间的距离，E为3×3阶单位矩阵，A1为力平衡系数矩阵，且有

点i与点i+2 (i=2,3,6,7)之间竖直梁的力平衡方程为：

(7)

式中，li,i+2为点i与点i+2之间的距离，A2为力平衡系数矩阵，且有

根据支链中各个单元的受力分析，节点i处作用力与反作用力关系为：

(8)

综合式(2)、(4)和式(5)~(8)，可求解得折叠梁左支链的柔度方程为：

u1=c1F1

(9)

式中，

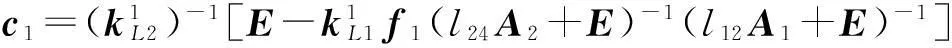
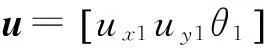
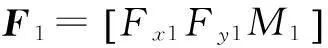
由式(9)，通过坐标变换可得折叠梁右支链的柔度方程：

(10)

3弹性折叠梁的刚度模型

对弹性折叠梁整体分析时，左、右支链末端的转动角度Δθ相等，且左、右支链末端y向位移的差值Δy与两支链末端间的距离d的比值和刚性梁的转动角度的正弦值相等，即Δy/d=sin(Δθ)。由于转角Δθ较小，则有Δy/d=Δθ。同时刚性块连接也使得两支链上端x向位移相等，根据上述分析及式(9)、(10)得：

(11)

由作用力与反作用力的关系及弹性折叠梁的整体受力情况可得：

(12)

根据左右两支链间的力平衡关系可得：

F1=Kt1F

(13)

(14)

联立式(9)、(10)、(13)、(14)得：

u1=c1Kt1F

(15)

(16)

由结构变形分析可知，弹性折叠梁的位移为：

(17)

(18)

根据弹性折叠梁的柔度模型，即可得到对应的刚度方程为：

F=kzu

(19)

4数值算例

对于图1所示弹性折叠梁，给定主要结构尺寸为l1=17mm，l2=16mm，h=1mm，z轴方向厚度为b=5mm，左右支链运动端间的距离d=6mm。材料弹性模量E=197Gpa，泊松比为0.25。对弹性折叠梁施加不同的力，可根据式(17)求得弹性折叠梁的输出位移，并应用ANSYS软件建立弹性折叠梁的有限元模型并进行分析，得到施加不同力的情况下，弹性折叠梁的输出位移，所得数据如表1所示。

由表1可知，当只有Fx作用时，其末端y向位移相对x向位移很小，y向位移可认为为零。当只有Fy向力作用时，其末端最大位移为y向。当只有力矩作用时，转动角度较大，但其末端x向位移不能忽视。可见，当施加特定载荷时，对于主载荷方向的变形，理论计算结果和ANSYS分析结果比较接近，因此对于主功能方向的变形分析可以基于刚度模型进行，但是在分析其他方向的牵连变形时候，理论计算值比较小，但实际的ANSYS分析结果显示变形不能忽视。

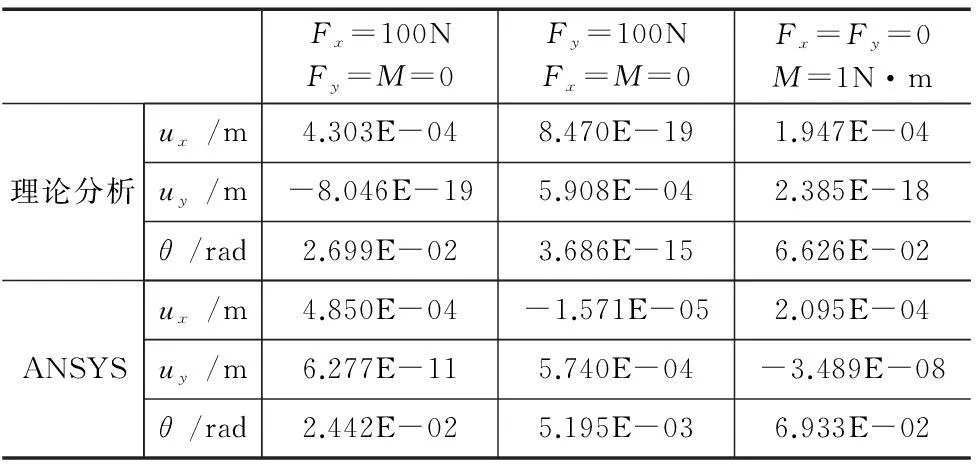
表1　不同外部载荷下弹性折叠梁的变形

5结论

为了有效提高微动平台的行程范围，提出一种弹性折叠梁结构。首先将整体结构划分为横梁和竖直梁两种不同单元，并建立相应的刚度方程，然后和各个节点的力平衡方程相结合，得到单侧结构的刚度方程。再根据结构的对称性，建立另一侧结构的刚度方程。最后根据两侧结构的变形协调关系推导出弹性折叠梁的整体刚度矩阵。最后给出了数值算例，表明刚度建模方法在分析驱动载荷方向的变形时候偏差很小，但是其他方向的牵连变形不能忽视。

[参考文献]

[1] YONG K Y, LU T F, HANDLEY D C. Review of circular flexure hinge design equations and derivation of empirical fomulations[J]. precision Engineering, 2008, 32(2): 63-70.

[2] 贠远，徐青松，李杨民．并联微操作机器人技术及应用进展[J]. 机械工程学报，2008，44(12)：12-23．

[3] 张彦斐, 宫金良. 2自由度大行程微定位平台结构与参数设计[J]. 机械工程学报, 2010, 46(23): 30-35.

[4] Gosselin C. Stiffness mapping for parallel manipulators[J]. IEEE Transactions On Robotics and Automation, 1990, 6(3):377-382.

[5] 付红栓, 赵恒华, 杨辉. 3-TpT型并联机床静力学及刚度研究[J]. 组合机床与自动化加工技术,2013(1): 42-44.

[6] 石志新,罗玉峰,陈红亮,等.含有柔性铰链并联机器人的刚度分析及刚度优化配置[J].机械设计与制造,2005(7): 92-93.

[7] 宫金良,胡光学,张彦斐.以刚度为目标的微位移放大模块闭环设计方法[J].机械工程学报, 2012, 48(15): 58-64.

[8] 王海容，赵则祥，蒋庄德．大行程纳米分辨率加载机构的研制[J]. 机械强度，2001，23(4)：452-455．

[9] 田延岭，张大卫，闫兵．二自由度微定位平台的研制[J]，光学精密工程，2006，14(1)：94-99.

(编辑李秀敏)

Rigidity Modeling Analysis of a Kind of Flexible Folded Beam

LIU Bin,ZHANG Yan-fei,GONG Jin-liang

(School of Mechanical Engineering, Shandong University of Technology, Zibo Shandong 255049,China)

Abstract：Rigidity has a great influence on the drive travel of micro-positioning platform. In order to improve the range of micro-positioning platform, a kind of flexible folded beam is proposed to replace the traditional elastic thin plate structure. First, the whole structure is divided into two different elements, beams and carlings. The rigidity equation of the elements is also set up, then combined with the force balance equation of each node for achieving the rigidity equation of unilateral structure. Second, according to symmetry, the rigidity equation of the other side is also achieved. Finally, the whole rigidity matrix of flexible folded beam is deduced by the relationship of compatible deformation on the both sides. At the end of the thesis, a numerical example demonstrated that the rigidity modeling method has the tiniest deviation on the analysis of the deformation in the driven direction and a low accuracy in the relative deformation of other side, so the ANSYS analysis results shall prevail.

Key words：micro-positioning platform; flexible folded beam; rigidity

文章编号：1001-2265(2016)01-0036-03

DOI:10.13462/j.cnki.mmtamt.2016.01.010

中图分类号：TH164;TG506

文献标识码：A

作者简介：刘斌(1989—)，男，山东莱芜人，山东理工大学硕士研究生，研究方向为微纳机器人，(E-mail)570711500@qq.com；通讯作者：张彦斐(1977—)，女，河北衡水人，山东理工大学副教授，博士，研究方向为微纳机器人领域的设计研发，(E-mail)1392076@sina.com。

*基金项目：国家自然科学基金项目(61303006)；山东省优秀中青年科学家科研奖励基金项目(BS2012ZZ009)

收稿日期：2015-03-17