基于ANSYS正交试验的横梁减重设计*

伍　伟，黄美发，李学聪

(1.桂林电子科技大学 机电工程学院，广西 桂林　541004；2.桂林机床股份有限公司，广西 桂林　541004)



基于ANSYS正交试验的横梁减重设计*

伍伟1，黄美发1，李学聪2

(1.桂林电子科技大学 机电工程学院，广西 桂林541004；2.桂林机床股份有限公司，广西 桂林541004)

摘要：某公司数控龙门铣床的横梁部件原先采用经验设计，质量很大。为了减少质量，选取横梁部件的6个参数，采用L25(56)正交表得到25组试验方案。利用最小二乘法得到了最大变形量、一阶固有频率和质量的二阶响应面模型。建立了横梁减重设计的数学模型，并利用遗传算法进行求解，优化后最大变形量基本不变，一阶固有频率增加4.4%和质量减少13.67%。

关键词：正交试验；横梁；响应面模型；减重设计

0引言

数控机床作为工作母机，广泛应用于汽车、模具、航天、军工等机械领域。机床轻量化设计体现了绿色、经济和节能的现代制造技术要求，成为企业可持续发展一个很重要的内容[1-3]。某公司生产的数控铣床采用传统的类比和经验设计方法，造成质量较大，成本也随之增加，影响了企业的效益，很有必要对该数控铣床进行轻量化设计。

本文对铣床横梁部件的静动态性能进行分析，在保持该横梁静动态性能不变情况下，进行减重设计。选取了横梁6个参数进行正交试验设计，得到25组试验结果。利用最小二乘法拟合出了最大变形量、一阶固有频率和质量的响应面模型，并验证响应面模型精度。建立了横梁减重的数学模型，利用遗传算法进行求解。

1横梁的静动态特性分析

某企业自主研发的数控龙门铣床，横梁部件是影响龙门铣床性能的关键部件，且质量较大，因此对其进行减重设计。

将横梁的三维实体模型导入到有限元分析软件中，设置材料属性，并划分网格。

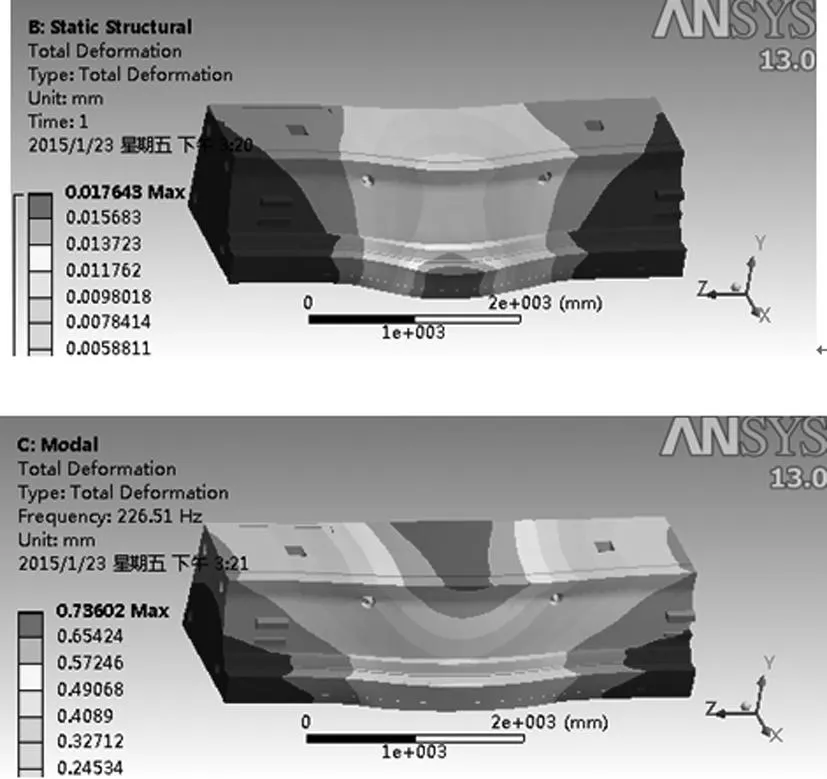
横梁与立柱螺栓连接，接触面施加固定约束。滑枕在横梁中间位置，伸出最长时，横梁所受载荷最大，是工作的极限工况[4]。分析在该工况下的静力学分析和模态分析，分析结果如图1所示。

由图1可以得到，横梁最大变形发生在下导轨中间的位置，变形量为0.017495mm，其它地方变形很小。一阶固有频率为216.98Hz，振型为横梁顶部中间位置前后摆动。

图1　横梁的总变形云图和一阶模态云图

2正交试验

2.1试验目的

正交试验设计是一种有效解决多因素优化问题的方法。基于正交试验对横梁结构进行尺寸参数的设计，可以得到各个参数对横梁性能的影响情况，为横梁的设计改进提供理论依据[5-6]。

采用正交试验设计方法进行方案设计，建立性能指标对参数的响应面模型，为优化设计做好准备。

2.2确定试验的因素、水平和指标

选取横梁结构的6个主要参数作为试验因素，如图2所示。6个试验因素分别是外壁厚x1，x向筋板厚x2，y向筋板厚x3，z向筋板厚x4，孔直径x5，方孔边长x6。每个试验因素考察五个水平。因素水平表如表1所示。

根据试验的目的，选取最大变形量y1、一阶固有频率y2和质量y3为试验指标。

图2　横梁截面图

水平因素x1x2x3x4x5x6120153515150150225202535130160330253025160170435301530140130540352020170140

2.3正交试验方案及结果分析

2.3.1正交试验方案

由表1，可知所研究的问题包含6个因素，每个因素5个水平，选用正交表为L25(56)，只需要进行25次试验，对这25种方案分别计算了最大静变形、一阶固有频率和质量这3个指标的数值，试验结果见表2。

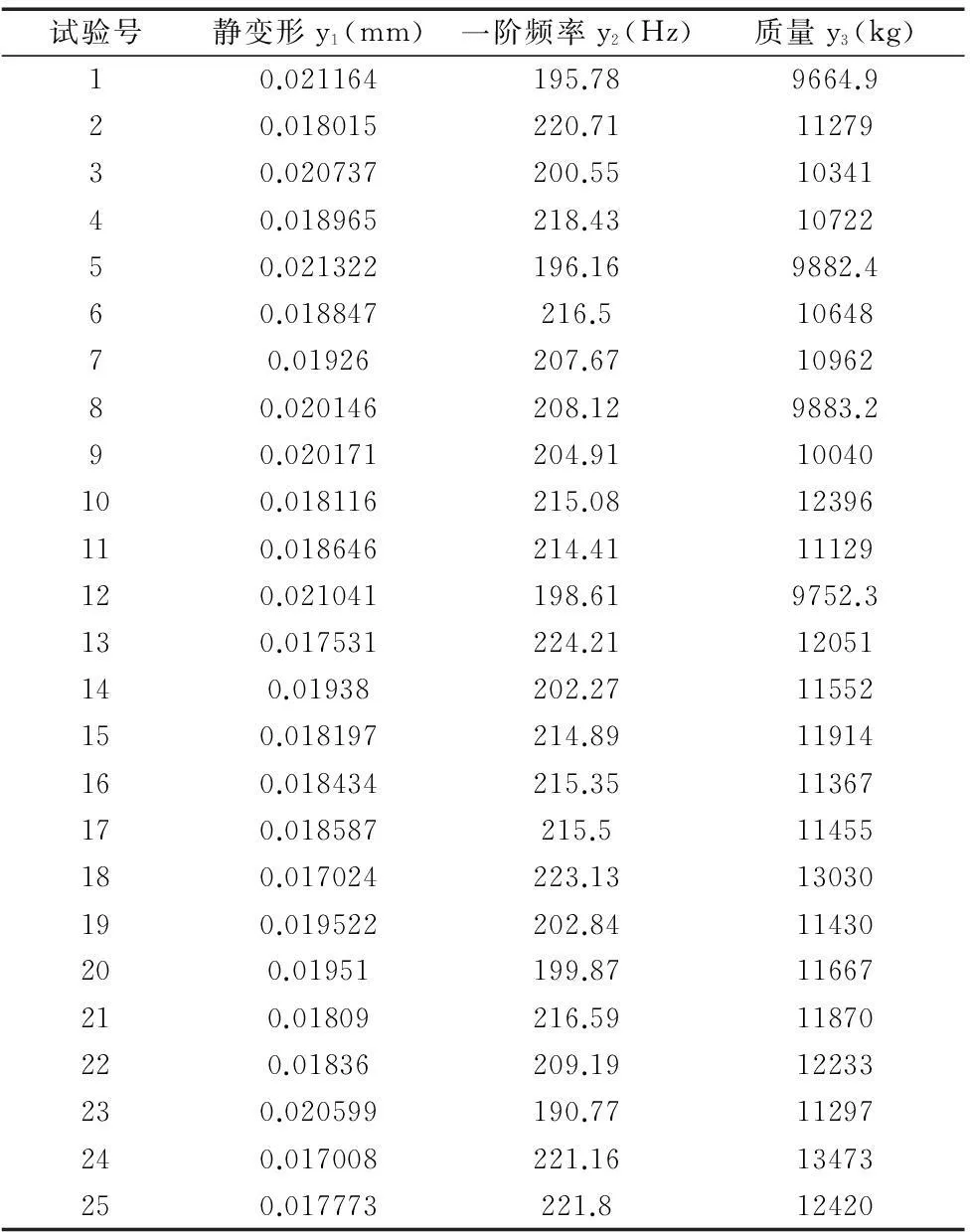
表2　正交试验方案计算结果

2.3.2结果分析

正交试验设计结果直观分析最重要的概念就是极差，通过极差分析，可以直观的知道因素对指标的影响，极差越大，说明该因素对指标的影响效果越明显。质量的极差分析结果见表3。

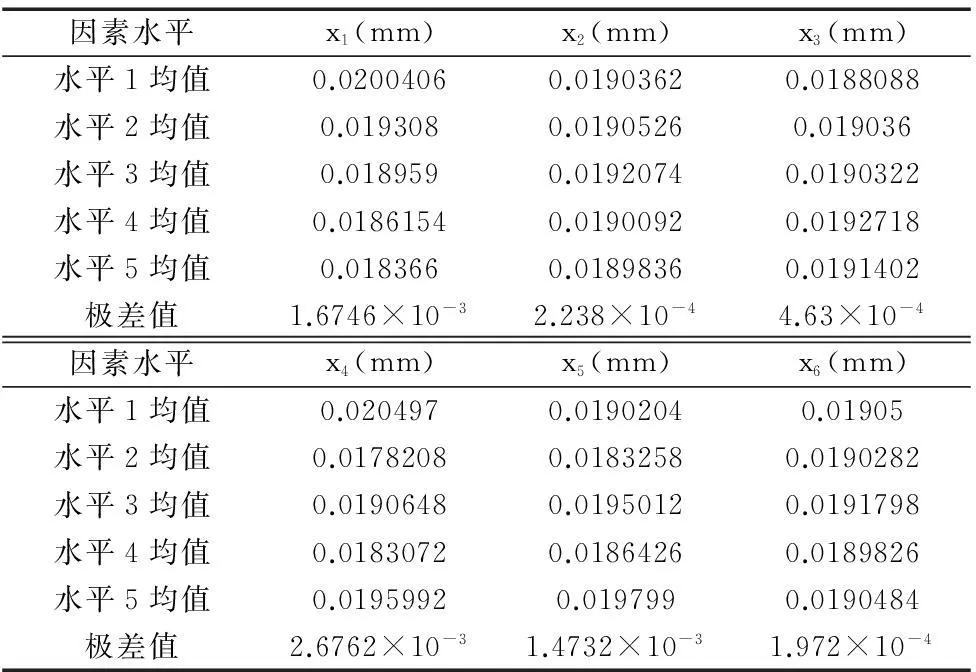
表3　横梁变形量的极差分析

由表3，得到了各个因素对变形量的极差值，通过对极差值比较，可以确定各因素对变形的影响主次顺序为：z向筋板厚>外壁厚>孔直径>y向筋板>x向筋板>方孔边长。

同理进行了一阶固有频率和质量的极差分析，各因素对一阶固有频率影响主次顺序为：z向筋板厚>孔直径> 外壁厚>y向筋板>x向筋板>方孔边长。各因素对质量影响主次顺序为：外壁厚>z向筋板厚>y向筋板>x向筋板>孔直径>方孔边长。

3响应面模型

为了使响应面模型更能准确表示出参数与指标之间的关系，采用不带交叉项的二次多项式形式表示响应面函数，并采用最小二乘法进行拟合，利用正交试验数据，通过matlab编程，可以拟合出最大变形量、一阶固有频率和质量的响应面模型[7-8]。

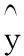
0.087943x3-2.1855x4+0.24121x5-0.28015x6+

(1)

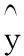
(2)

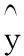
(3)

由公式计算可以得到最大变形量、一阶固有频率和质量的优度指标分别为：0.994，0.99594，0.99708。优度指标较高，说明拟合精度较高，为下一步进行优化提供了良好前提。

4建立数学优化模型及求解

4.1横梁优化数学模型

组成优化问题数学模型的三个基本要素是：目标函数、约束条件和设计变量[9]。

4.1.1目标函数

在保证横梁的最大变形量和一阶频率基本稳定的情况下，质量最小即：

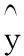
4.1.2约束条件

随着参数发生变化，最大变形量和一阶固有频率也会发生变化，要保证原横梁结构性能不降低，因此设置约束条件，最大变形量不大于0.017495mm，一阶固有频率不小于216.98Hz，即：

4.1.3设计变量

横梁外形尺寸由机床的规格决定，一般不宜改变，所以选取横梁内部筋板和孔为研究对象，包括6个主要参数，分别是外壁厚x1，x向筋板厚x2，y向筋板厚x3，z向筋板厚x4，孔直径x5，方孔边长x6。

参数上下限：

20

15

4.2数学模型求解

横梁结构最优尺寸是6个参数的组合问题，优化求解可能存在多峰问题。因此优化算法采用全局搜索方法，遗传算法具有较好的全局搜索能力，所以采用遗传算法求解。目前matlab工具箱集成了遗传算法，只需编写少量程序即可实现优化算法[10]。

因此采用matlab优化设计工具箱的遗传算法进行求解，计算得到优化的参数经圆整后参数取值分别为x1=27，x2=15，x3=15，x4=35，x5=130，x6=169。

5结果分析

根据优化的结果，对原横梁尺寸进行修改，并分析了改进横梁的最大变形量和一阶固有频率，如图3所示。

图3　修改后横梁的最大变形与1阶模态

原横梁和改进的横梁的性能进行对比，原横梁质量为13035kg，改进后横梁质量为11253kg，减少了1782kg，减少率为13.67%，优化结果效果明显。对比情况如表4所示。

表4　改进前后横梁性能或参数对比情况

6结束语

利用正交试验方法设计了25次试验，并采用最小二乘法拟合出了最大变形量、一阶固有频率和质量的响应面模型。建立了横梁轻量化的数学优化模型，利用遗传算法对数学模型进行求解，得到了较好的优化结果。此方法为机床部件优化提供思路。

[参考文献]

[1] 梁铖，刘健群. 五轴联动数控机床技术现状与发展趋势[J]. 机械制造，2010(48):5-7.

[2] Xu Yuxiang，Wang Keshe，et al. Review on Compound Optimization of Motion part in Machine Tool with Lightweight Design [C]. proceedings of 2009 International Conference on Modeling, Simulation and Optimization，2009.

[3] 孙守林，刘建栋，董慧敏，等. 机床主轴箱轻量化设计流程研究[J]. 组合机床与自动化加工技术，2014(12):14-18.

[4] 李焱，张磊，刘春时，等. 高速龙门五轴加工中心静刚度分析与结构优化[J]. 组合机床与自动化加工技术，2011(6):9-11.

[5] 闻邦椿，刘树英，陈照波，等. 正交设计─一种安排多因素试验的数学方法[M].北京:人民教育出版社，1976.

[6] 杨剑秋，王延荣. 基于正交试验设计的空心叶片结构优化设计[J]. 航空动力学报，2011(26):376-384.

[7] 任新见，时党勇，汪剑辉. 响应面试验设计的正交方法研究[J]. 山西建筑，2005(31):17-18

[8] 刘洁雪. 基于响应面法的集装箱船优化设计研究[D]. 天津：天津大学，2008.

[9] 于海莲，王永泉，陈花玲，等. 响应面模型与多目标遗传算法相结合的机床立柱参数优化[J]. 西安交通大学学报，2012(46):80-84.

[10] 雷英杰. MATLAB遗传算法工具箱及应用[M]，西安：西安电子科技大学出版社，2005.

(编辑李秀敏)

The Lightweight Design of Beam Based on ANSYS Orthogonal Experiment

WU Wei1, HUANG Mei-fa1, LI Xue-cong2

(1. School of Mechanical & Electrical Engineering, Guilin University of Electronic Technology, Guilin Guangxi 541004, China; 2. Guilin Machine Tool Co., Ltd, Guilin Guangxi 541004, China)

Abstract：The beam in gantry milling machine in a certain company is designed by using empirical method and the mass is large. In order to reduce mass, 6 parameter are selected and 25 experiment schemes are designed according to L25(56) orthogonal table. The response models of the maximum deformation, the first natural frequency and the mass are obtained by the least squares method. The mathematical model of lightweight design is established and solved by genetic algorithm. The maximum deformation is almost invariable, the first natural frequency is increased by 4.4% and the mass is deduced by 13.67%.

Key words：orthogonal experiment; beam; response surface model; lightweight design

文章编号：1001-2265(2016)01-0042-04 1001-2265(2016)01-0039-03

DOI:10.13462/j.cnki.mmtamt.2016.01.012 10.13462/j.cnki.mmtamt.2016.01.011

中图分类号：TH122；TG65

文献标识码：A

作者简介：伍伟(1988—)，男，湖南永州人，桂林电子科技大学硕士研究生，研究方向为机床结构优化设计及轻量化研究，(E-mail)wuwei198812@163.com；黄美发(1962—)男，广西蒙山人，桂林电子科技大学教授，博导，研究方向为数控机床开发及机床精度、新一代GpS理论，(E-mail)hmhmf@guet.edu.cn。

*基金项目：国家自然科学基金(51365009)；广西科学研究与技术开发计划项(桂科能1355012-5)；广西硕士研究生科研创新项(YCSZ2014134)

收稿日期：2015-02-08；修回日期：2015-03-19