声速对河口区域回波测深的精度影响研究

陆 伟

（1.交通运输部天津水运工程科学研究所，天津300456；2.天津水运工程勘察设计院天津市水运工程测绘技术重点实验室，天津300456）

声速对河口区域回波测深的精度影响研究

陆 伟1，2

（1.交通运输部天津水运工程科学研究所，天津300456；2.天津水运工程勘察设计院天津市水运工程测绘技术重点实验室，天津300456）

回波测深是目前水深测量采用的主要原理，声速是回波测深精度的重要影响因素之一。文章分析了声速影响水深测量精度的基本理论，包括声速误差引起的垂直差、声线弯曲引起的测深差、回波位置偏移以及声速时空变化引起的测深差；同时以瓯江口水深测量项目为例进行了详细量化计算，归纳总结了河口区域水深测量期间声速对测深精度的影响，并就减少相应误差给出了参考建议。

水深测量；声速；测深精度；瓯江口

回波测深是目前水深测量采用的主要原理，典型作业方式有单波束测深、多波束扫测等。回波测深的基础理论是通过换能器向下发射声波，再经换能器接收回波，根据声速及往返的时间计算水深［1-2］。

运用该理论要实现精确测深的前提是假定声音在水中沿直线传播，即在水中不发生折射。瓯江口等河口水域因受温度、盐度与水深变化的影响，剖面各层声速并非完全相同，因声波折射的产生，声线将发生弯曲。另一方面，且受潮汐及江海换流影响，声速时空变化特征比较明显，具有类似潮周期现象，同一位置日变化量及不同位置声速差异均体现明显。声速误差对于瓯江口水深测量的精度影响不容忽视，具体体现在声速误差引起的测深差、声线弯曲引起的测深差、回波位置偏移以及声速时空变化引起的测深差四部分。

1 平均剖面声速引起的测深差

水体剖面声速变化是连续的，按照水体的微量分层逐渐变化。假定声波在水中沿直线传播且方向垂直向下，对剖面声速进行离散处理，计算水深值如下（不考虑换能器吃水）

式中：vi、ti分别表示第i个分层中的声速值及对应单程传播时间。

式（1）表明，声波在水中沿直线传播且方向垂直向下时，测量水深与声速呈严格线性比例关系。在实际工作时往往采用平均剖面声速代表整个剖面声速［3-4］，水深测量差值ΔHv与平均剖面声速差值Δvˉ也呈线性比例关系

该关系相对简单，通过精确测量声速与合理计算平均值，同时采用综合检校板在不同水深时进行实际比对检测即可有效减少或消除由此引发的水深差值［5］。

2 声线弯曲引起的测深差

声波在不同声学性质介面将发生折射现象，导致声线弯曲，而不是像均匀介质声波传播一样呈直线形式。在实际海水中，水体剖面各层的声学性质不可能是均匀的，因此，不同的声速在海水中构成一系列声速层［6］。在水深测量时，换能器发身声波信号在向下传播时，必然发生折射，造成声线弯曲，以至于测量水深值为弯曲声线长度，而非垂直深度，弯曲声线长度与垂直深度之差即为引起的水深差ΔHb。如图1所示，α1为换能器声波初始入射角，αi为各分层入射角。

图1 水中声线弯曲Fig.1 Sound ray bending under water

对水体剖面进行离散分层后，各层水深差值及总测深差值计算如下

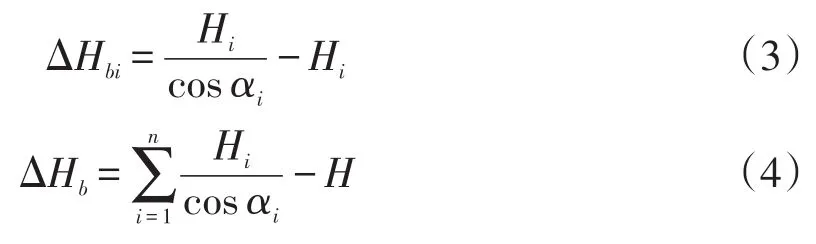
研究表明，声波在水中的传播同样符合Snell折射定律［6］，即

上述公式表明，对于某一位置处水深测量而言，声线弯曲引起的水深差值大小主要由声速剖面变化、声波入射角决定。

2013年11～12月瓯江口水深测量项目中，按0.5 m固定厚度分层进行了声速剖面测量。图2是某时刻瓯江口实际声速剖面曲线。

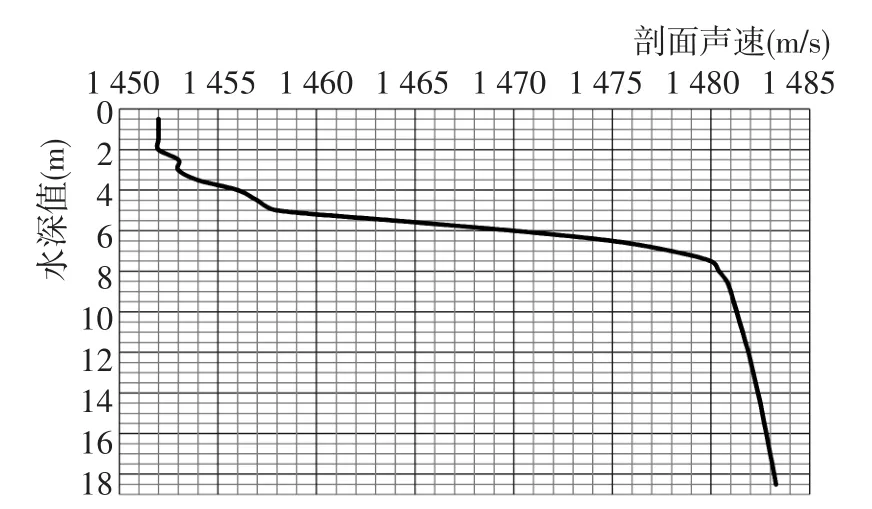
图2 瓯江口某时刻声速剖面Fig.2 Sound velocity profile of Oujiang Estuary in a moment

在此情况下，当已知初始入射角α1时，根据式（5）可推算各层入射角，既而通过式（3）、式（4）可计算各分层水深误差及整体差值ΔHbi、ΔHb。

对α1依次取值0°～20°时，计算整体水深误差ΔHb与α1的关系曲线如图3。结果表明，在瓯江口水深近20 m、剖面声速变化累积达30 m/s时，ΔHb随着α1在0°～20°内取值的增大而不断增加，且呈指数增长。实际测量时，为有效减少误差累积，应尽量将初始入射角在6°以内，即使考虑换能器的波束开角以及最浅水深原则，也应尽量将初始入射角控制在10°以内（单波束测深仪波束开角通常在3°～10°［7］）。

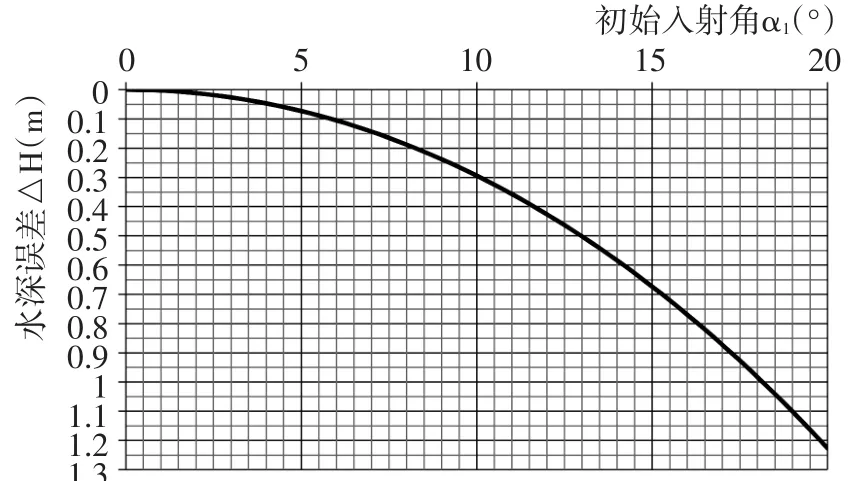
图3 水深误差与入射角关系Fig.3 Relationship between sounding error and incident angle

另外，分别对α1取值5°、15°并计算各分层水深误差ΔHbi的变化情况，如图4所示，对比图2不难发现，ΔHbi随深度的变化剖面声速变化具有极强的相关性，如图4所示。

3 回波位置偏移引起的测深差

水深测量时，需要保持定位中心与测深点的平面位置一致性，实际操作过程中要求将GNSS定位中心安置在测深换能器正上方或通过相对距离关系进行归算，以确保其一致性［8］。然而因声波折射声线弯曲的原因，海底声波反射点并非为换能器正下方点位，如图1中P1为海底声波反射点，是实际测深位置，而测量记录的定位测深点为P，由此引起的P-P1的距离称为回波位置偏移。

回波位置偏移不仅造成测深点的平面定位误差，同时也可能引起测深误差。根据图1所示几何关系，平面定位误差ΔS可由式（6）计算。

同样以上述瓯江口声速剖面为例，当α1依次取值0°～20°时，计算位置误差ΔS随α1变化曲线如图5。通过线性拟合，计算斜率k=0.34，拟合相关系数R=0.999 8，拟合标准差σ=0.037 m。计算结果说明回波位置引起的平面定位误差基本与声速剖面变化无关，仅与声波初始入射角有关，且呈近似线性关系。测量过程中，应根据测图比例尺所容许的平面定位限差合理控制换能器入射姿态。

回波位置偏移引起的测深误差大小主要取决于海底微地形平坦程度。当海底平坦，测深误差ΔHh可近似按式（7）进行计算与工前评估，以制订相应技术方案减少或避免测深误差的产生。当海底微地形变化较大，尤其是陡峭山崖附近或礁石区域时也应尽可能控制好换能器的入射姿态。

式中：ΔS为平面定位误差，i为海底坡比。

4 声速时空变化引起的测深差

声速的时空变化是指在一定范围内或一定时间段内，同一位置不同时刻或是同一时刻不同位置声速的差异，声速时空变化在河口区域体现的尤为明显。瓯江口既具有典型海洋潮汐特征，且流速急潮差大，同时受上游淡水径流影响严重。随着涨潮时大量海水的涌入以及落潮时上游径流淡水的补充，在狭长的河口区域时空变化极为典型。

2013年11～12月瓯江口水深测量实测资料表明，在空间分布上，同一时刻东西方向（上下游方向）平均剖面声速每公里变化差值2～3 m/s，南北方向基本无差异；在时间分布上，每天的涨潮时段声速较大，最大约1 480 m/s，落潮时段声速较小，最小约1 450 m/s，一个潮周期变化量近30 m/s。在涨潮、落潮阶段，其剖面声速也差异较大，换水期间，底层水体先行更换，声速也先行变化，表层后行更换，声速也后行变化，表底层剖面声速最大差异也近30 m/s。

同一时刻，南北方向基本无测深误差，东西方向每差1 Km，估算最大深测差值Δhmax为

同一位置，一个潮周期内涨潮、落潮期间估算最大深测误差Δhmax为

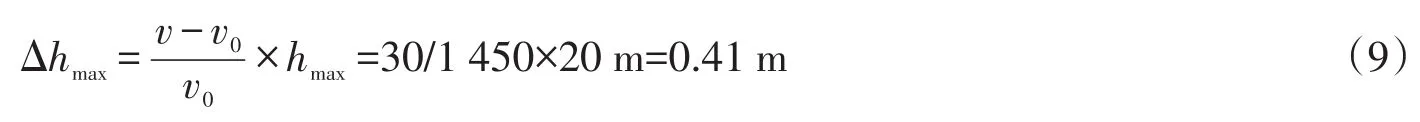
根据上述分析及估算，瓯江口内水深测量的声速空间变化引起的测深差值相对较小，而时间变化引起的测深差值较大。而相关规范在声速测量时给出的参考是声速剖面距离间隔不宜大于6 Km、时间间隔应小于6 h［8］，在忽略瓯江口声速时空变化特征情况下，直接采用此参考值将极易引起测深误差超限。要充分保证测深精度，必须大大缩小声速测量的时间与空间间隔。

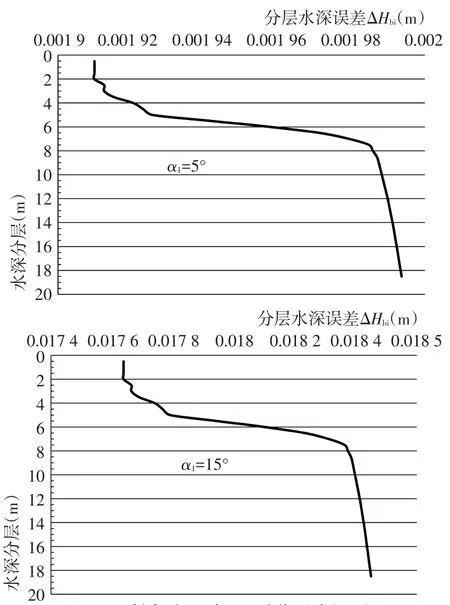
图4 入射角为5°或15°时分层水深误差Fig.4 Sounding error of depth layers while incidentangle equals 5 or 15 deg.

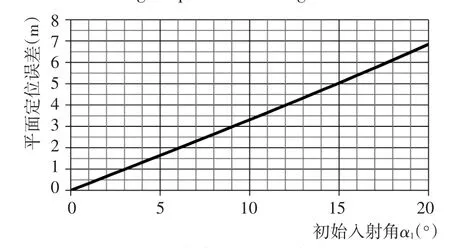
图5 平面定位误差与入射角关系Fig.5 Relationship between horizontal positioning error and incident angle

5 结论与建议

瓯江口由于海水与淡水交替换流，导致声速复杂多变，声速剖面具有分布不均匀、时空变化大等特点，由此产生的声速误差对测深影响主要体现在本文分析的四个方面，对于其它类似河口区域，该分析与结论同样适用。

根据分析理论与实际经验，对河口区域水深测量给出相关建议如下：

（1）声速剖面不均匀将引起水深计算产生差值，水深计算处理时，应避免采用单一声速值改正，尽量采用剖面声速改正，或准确计算平均剖面声速，同时运用综合检校板对测深比例误差进行检查。

（2）声线弯曲对测深影响极大，具体数值主要取决于剖面声速变化与声波初始入射角。测深误差与入射角呈指数增长，在瓯江口区域极易达到数十厘米误差。剖面声速变化为水域固有环境特征不能改变，作业时应尽可能缩小声波初始入射角，以不超过10°为宜，减少测深差的不断累积。

（3）回波位置偏移引起的平面定位误差基本与声速剖面变化无关，与声波初始入射角呈线性关系，作业时根据应测图比例尺容许定位限差进行综合判断，减少声波入射角以避免平面定位误差的超限。

（4）在平坦区域回波位置偏移引起的测深差值较小，在岸波、礁石、岛屿附近等海底微地貌变化较大区域，回波位置偏移引起的测深差值也不忽视，测量时尽量选择合适海况条件、有效控制测深姿态。

（5）河口区域声速时空变化较大，应加密声速剖面数据采集点，同时缩小采集时间间隔［9］，确保测量所采用声速剖面合理有效，防止因声速时空变化引起测深误差超限。

［1］黄珍雄.单波束水下地形测量精度的改进方法研究［D］.南昌：东华理工大学，2013.

［2］吴振南.浅论回声测水深的声速修正［J］.科技资讯，2007（18）：64.

［3］关致和，赵先龙，邵海涛，等.HY1200声速剖面仪计算测深仪声速改正数方法［J］.海洋测绘，2006，26（1）：66-67.

GUAN Z H，ZHAO X L，SHAO H T，et al.The Correction Method for the Sound Velocity Data of HY1200 Sound Velocity Profiler ［J］.Hydrographic Surveying and Charting，2006，26（1）：66-67.

［5］桑金.基于GPS技术的精密水深测量方法研究［D］.天津：天津大学，2006.

［5］陆伟.单波束水深测量及其质量控制-以温州港水下地形测量项目为例［D］.武汉：武汉大学，2015.

［6］孙革.多波束测深系统声速校正方法研究及其应用［D］.青岛：中国海洋大学，2007.

［7］胡译文，陆伟.波浪对水深测量测深精度影响分析［J］.水道港口，2015，36（2）：172.

HU Y W，LU W.Impact of Wave on accuracy analysis of sounding［J］.Journal of Waterway and Harbor，2015，36（2）：172.

［8］TJS 131-2012，水运工程测量规范［S］.

［9］丁继胜，吴永亭，周兴华，等.长江口海域声速剖面特性及其对多波束勘测的影响［J］.海洋通报，2006，25（3）：5. DING J S，WU Y T，ZHOU X H，et al.The Characteristics of SVP Near the Changjiang River Estuary and the Effect on the Multi⁃beam Echo Sounder System［J］.Marine Science Bulletin，，2006，25（3）：5.

Study on sounding accuracy impacted by sound velocity in the estuary

LU Wei1,2
（1.Tianjin Research Institute for Water Transport Engineering,Tianjin 300456,China;2.Tianjin Key Laboratory of Surveying and Mapping for Waterway Transport Engineering,Tianjin Survey and Design Institute for Water Transport Engineering,Tianjin 300456,China）

Echo sounding is the main principle of the current sounding，and sound velocity is one of the impor⁃tant factors impacting the accuracy of echo sounding.In this paper,the basic theory of sounding accuracy impacted by sound velocity was analyzed,which including the vertical error,errors caused by the bending of the sound,the er⁃ror caused by echo location deviation and the error caused by the temporal and spatial variation of sound velocity. The detailed computation based on the Oujiang Estuary sounding project was also carried out in this paper,and some suggestions were given to reduce the sounding error in the estuary projects.

sounding;sound velocity;sounding accuracy;Oujiang Estuary

P 715

A

1005-8443（2016）03-0316-04

2015-10-10；

2015-12-30

陆伟（1985-），男，湖南省衡阳市人，工程师，主要从事海洋测绘及地理信息工程相关研究工作。

Biography：LU Wei（1985-），male，engineer.