基于CFD-DEM耦合方法的近床面水流泥沙运动模拟研究

苏东升，张庆河，孙建军，李明星

（天津大学水利工程仿真与安全国家重点实验室，天津300072）

基于CFD-DEM耦合方法的近床面水流泥沙运动模拟研究

苏东升，张庆河，孙建军，李明星

（天津大学水利工程仿真与安全国家重点实验室，天津300072）

基于CFD-DEM方法，采用流体计算软件OpenFOAM、颗粒运动模拟软件LIGGGHTS及CFDEM耦合库，建立流体—颗粒运动耦合模型，并利用模型研究不同水动力条件下近床面流体与颗粒的运动规律。模拟结果表明，模型能较好模拟近床面水流紊动特性及雷诺应力分布，也能较准确刻画出颗粒未起动、推移质输沙及推移质和悬移质共同输沙的三种状态，计算得到的推移质单宽输沙率与实验结果及经验公式吻合较好。

CFD-DEM耦合模型；近床面水流；紊流强度；推移质输沙

水流作用下的近床面泥沙运动是河流动力学研究的重要课题，一直受到国内外学者的重视，目前已有大量理论、实验及数值模拟的文献发表［1-2］。近年来，计算流体力学（CFD）的广泛应用及离散单元法（DEM）的日臻完善，使得水流泥沙运动研究从宏观研究进入细观尺度的数值模拟研究［3-5］。CFD与DEM的耦合数值模型可以描述泥沙颗粒在水体中的运动过程，从细观尺度刻画大量泥沙颗粒在近床面运动的细节，并可以在此基础上进一步总结近床面水流泥沙宏观运动规律［6-7］。与直接数值模拟（DNS）［8］、浸润边界法（IBM）［9］及格子玻尔兹曼（LBM）［10］等可以描述颗粒运动受力的方法相比，CFD-DEM耦合模型对于颗粒本身并不作解析，减少了对计算资源的需求，因而可以应用于描述局部冲刷等颗粒数目上百万的实际问题，具有较为广泛的应用前景。为此，本文将基于计算流体力学开源软件OpenFOAM®和离散颗粒开源软件LIGGGHTS®以及二者耦合的开源软件CFDEM®，建立描述水流泥沙运动的细观模型，研究不同水流动力条件下近床面水体的紊动特性与泥沙颗粒的运动规律。

1 CFD-DEM耦合模型

1.1 模型简介

CFDEM是基于Linux平台，采用C++语言编写的一款面向对象的CFD-DEM开源耦合库。CFDEM耦合库将OpenFOAM模拟的流体运动与LIGGGHTS计算的颗粒运动之间以传递动量项的方式进行耦合，建立了流体与颗粒的模拟框架［11］。

1.2 流体运动控制方程

OpenFOAM中，考虑颗粒组分影响的三维流体运动的控制方程由以下连续性方程和动量方程组成

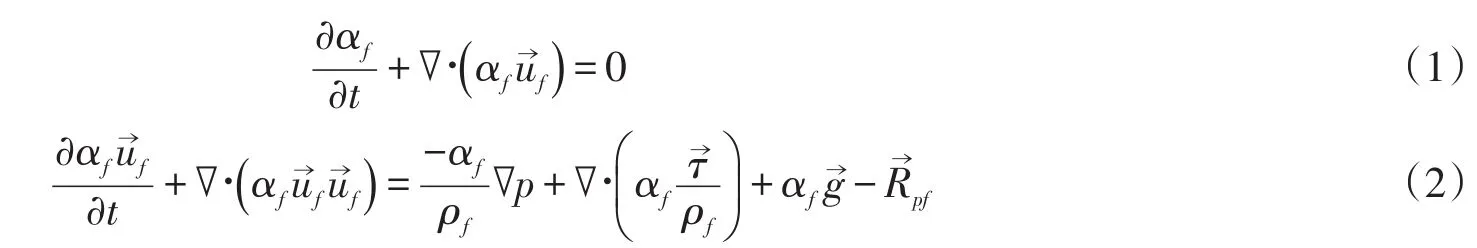
式中：αf为流体所占据的体积分数；为流体的速度向量；p为流体压力；g→为重力加速度向量；为流体有效应力的张量；为颗粒与流体之间交换的动量项。

1.3 颗粒运动控制方程

在LIGGGHTS颗粒模型中，颗粒运动遵循牛顿第二定律，其控制方程主要包括平动与转动两方面，具体形式为

1.4 耦合过程

在耦合过程中，OpenFOAM采用大涡模拟（LES）来描述流场中的紊动特性，亚格子应力采用Smagorinsky模型［12］；LIGGGHTS中采用Hertz⁃Mindlin无滑移“软球”模型［13］计算接触颗粒之间的作用力。具体的耦合过程如图1所示。

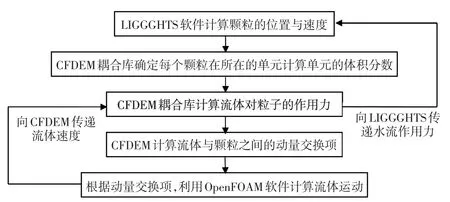
图1 颗粒与流体运动的耦合过程Fig.1 Procedure for coupling of particles and fluid

2 近床面水流泥沙运动的数值模拟

2.1计算区域及模拟参数设定

流体的计算域为长方体，大小为x×y×z=0.12 m×0.06 m×0.04 m。流体的流动方向为x轴正方向，y轴为展向，z轴为垂向。计算网格为结构化网格，水平和垂向网格步长为1.0 mm。颗粒运动的计算域与流体重合，颗粒简化为直径为0.5 mm的球体。流体与颗粒计算的时间间隔分别为Δtf=10-3s和Δts=10-5s，颗粒计算100步后与流体进行一次耦合。计算流体为清水，其密度ρf=1 000 kg/m3，动力粘滞系数μ=10-6kg/m·s。用于颗粒计算的Hertz⁃Mindlin无滑移“软球”模型参数如表1所示。

表1 模型中颗粒与流体参数Tab.1 Particle and fluid parameters used for the present simulation

2.2算例设计及模型初边值

为了研究不同流速下流体与泥沙运动的规律，本文共设计九组算例。算例1～9中，流体沿x方向的目标平均流速＜＜u→f＞＞从0.2 m/s增加至1.0 m/s，间隔为0.1 m/s。为了保证计算域底边界处泥沙颗粒不被全部冲起，对于目标平均流速＜＜u→f＞＞=0.2～0.6 m/s的算例，底床泥沙颗粒的厚度取为1.7 mm，共计115731个颗粒；对于目标平均流速＜＜u→f＞＞=0.7～1.0 m/s的算例，底床泥沙颗粒的厚度取为5.0 mm左右，共计330 023个颗粒。

泥沙颗粒随机均匀平铺在计算区域底部，初始计算时，使泥沙颗粒保持固定只计算由体积力驱动的水体。待计算流场紊流充分发展并稳定后，使底床颗粒开始运动，再进行10 s的模拟。流场的初始剖面由对数律给定。为保证结果精度，取底床泥沙释放后5～10 s的数据进行分析。

对于流体，x轴与y轴方向均设为循环边界，顶边界设为滑移边界，底边界为无滑移边界。对于颗粒计算，计算区域四周均为循环边界，顶边界与底边界为墙壁。

3 模拟结果分析

3.1 流体运动分析

此次模拟分为两个阶段。第一阶段，水体由符合对数流速分布的初始剖面开始，受到体积力驱动，在固定泥沙颗粒的粗糙床面上运动，直至紊流发展充分。为观察模拟流场的紊动特性，图2和图3给出了目标平均流速的算例在紊流充分发展后的流速剖面图。图2-a为接近泥沙颗粒顶部z=2.0 mm处的紊流流速剖面，图2-b为z=2.0 mm与y=0.06 m两平面交线处瞬时流速u和w沿y轴方向的分布。图3-a、3-b两图分别为x=0 m与y=0.06 m处紊流流速的分布图。

在接近泥沙颗粒顶部的z=2.0 mm轴剖面处，由图2-a可以清楚地看到瞬时流速形成了低流速带与高流速带相间排列的结构特征，与Kline等利用氢泡技术在光滑床面上观察到的条带结构相似［14］。图2-b中底床流速分量u和w沿y轴大小间隔分布的间距虽不尽相同，但其平均值却相对稳定，其无量纲化后距离约为424。

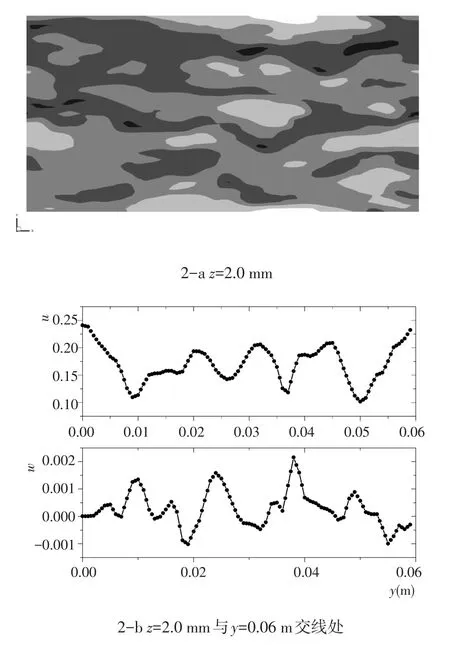
图2 充分发展的近底紊流流速分布Fig.2 Distribution of fully developed turbulent flow profile near bottom

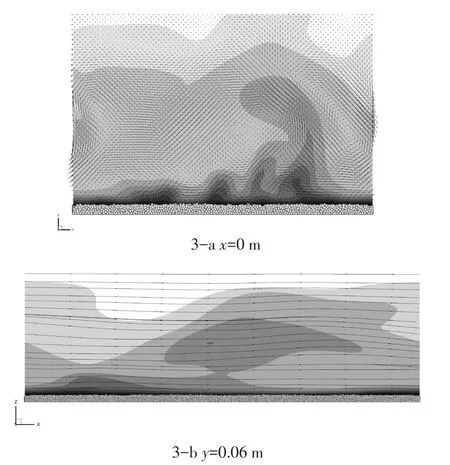
图3 充分发展的侧边界紊流流速分布Fig.3 Distribution of fully developed turbulent flow profile at lateral boundary

从图3-a中的x=0 m剖面可以看到，底部附近的低速流体被举升抬离底床，发生“喷射”现象。图3-b中进入主流区的低速流体受到高速流体的冲击，产生大量紊动，低速流体被携带至下游方向，发生“清扫”过程。模拟中包含低速流体喷射与高速流体清扫的紊流猝发现象与学者对于此现象的一般认识吻合［15-16］。

模拟第二阶段，固定在底床的颗粒由静止状态释放，底床泥沙颗粒在受到水流作用后起动，随着水流向下游运动。由于床面泥沙颗粒厚度不同，本文将9组算例按照初始泥沙床面高度分为小流速组0.2～0.6 m/s）和与大流速组。图4中4-a与4-b为分别为和1.0 m/s两组代表算例在第二阶段的时均流速剖面图，图中的z坐标以计算域底边界为零点。两组代表算例在模拟区域底边界上的流速均为零，说明底边界上的泥沙颗粒并未运动，保证了泥沙厚度设置的合理性。图4-a中的流速较小，在初始泥沙床面顶部高度以下的模拟流速值均接近零；而对于图4-b中算例，初始床面顶部高度以下小范围内流速不为零。从以下3.2节泥沙运动的分析中可以得到，小流速组的算例泥沙运动形式为未起动或推移质运动，泥沙均在初始床面附近运动，此时初始床面高度附近被泥沙占据，此处的流速接近于零；大流速组的泥沙运动为推移质与悬移质共存的形式，初始床面高度附近的泥沙被水流悬扬起来，因而此处的流速不为零，而且流速过渡较平滑。

初始床面以上的流速利用如下对数流速公式进行拟合

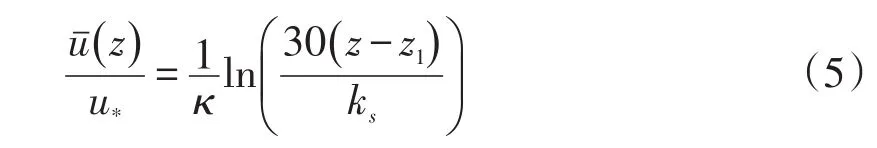
式中:κ为卡门常数取0.4，z1为理论床面距计算域底部高度，z为距计算域底部高度，ks为等效粗糙高度。对于m/s的算例，摩阻流速u*=0.045 m/s，理论床面高度z1=1.68 mm，等效粗糙高度ks=1.14D；对于的算例，摩阻流速u*=0.090 m/s，理论床面高度z1=4.80 mm，等效粗糙高度ks=3.13D。拟合结果如图4-a与4-b所示，左上角小图中z轴以理论床面为0点绘制，从图可以看出平均流速均匀分布在理论曲线两侧，水流模拟结果是较为合理的。

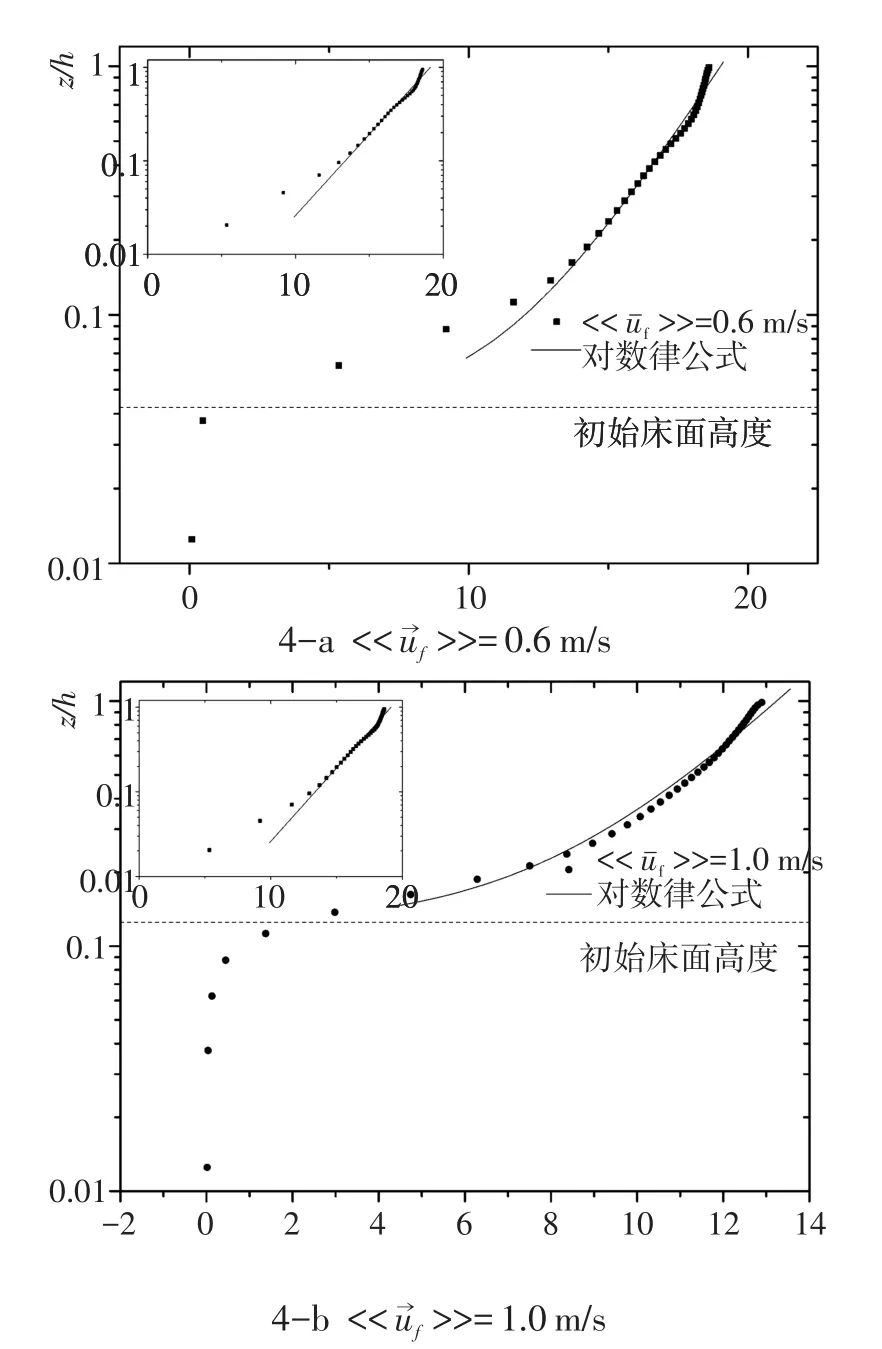
图4 时均流速剖面Fig.4 Time⁃averaged velocity profile

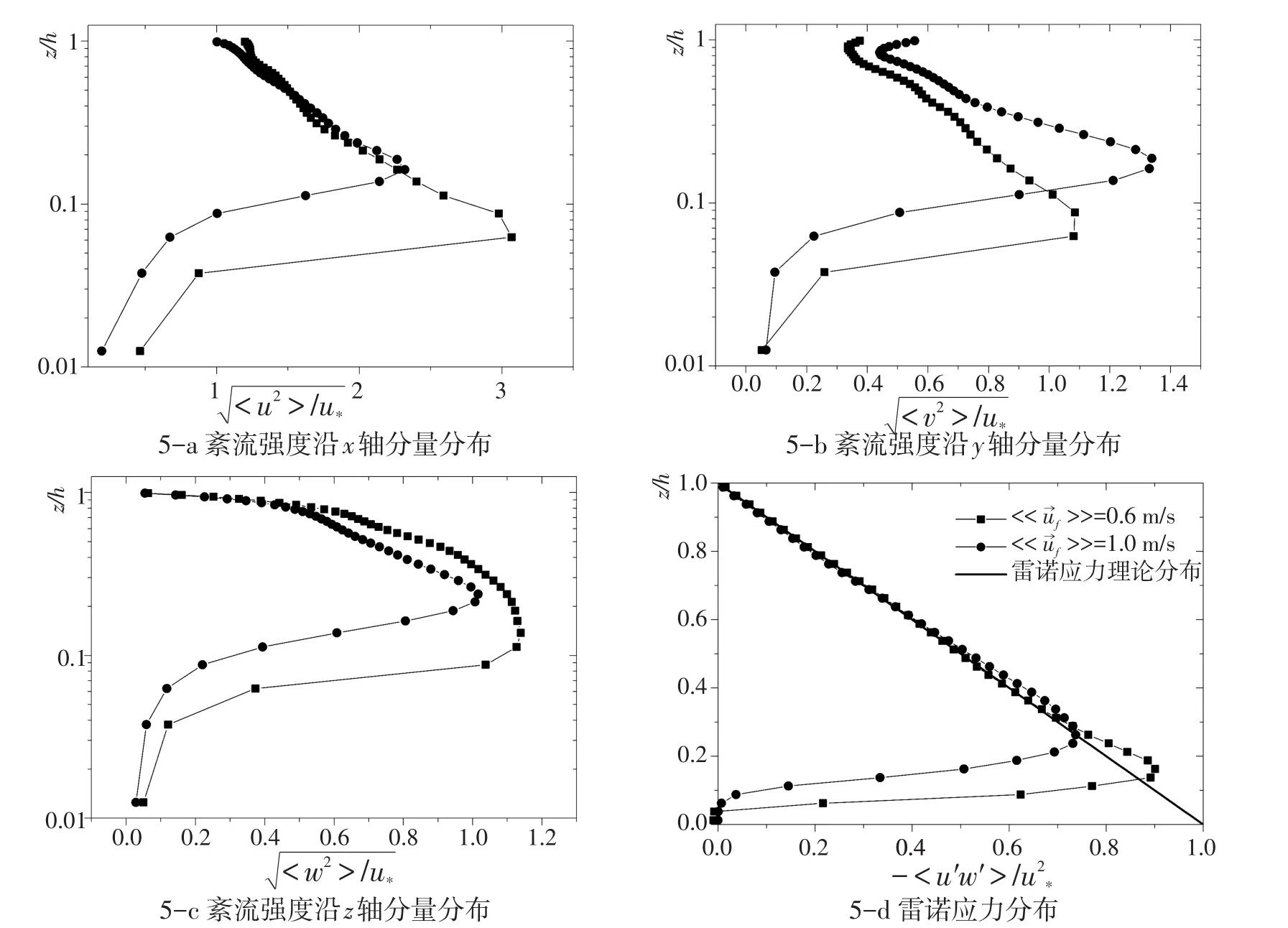
图5 紊流强度分量与雷诺应力沿z轴方向的时间平均分布Fig.5 Distribution of relative turbulence intensity components and relative Reynold stress along the z axis

流体紊动强度的分布对于泥沙的运动有着至关重要的影响。图5中的5-a、5-b、5-c图为小流速代表组与大流速代表组按时间平均后的相对紊动强度分量沿z轴方向的分布图。两组紊动强度的峰值皆位于初始床面顶部附近，此处水流与泥沙相互作用最为剧烈。水流的紊动作用带动泥沙的运动，泥沙的运动改变了床面的形状，使得水流在床面附近的流动更为复杂，更容易产生紊动。在靠近模拟区域底边界被泥沙大量占据，水流在孔隙中的流动受到较大限制，紊动强度接近于零。对于接近模拟区域顶部，流体沿x轴与y轴方向的流动受床面影响有限，故5-a、5-b中的紊流强度较小。流体沿z轴方向的速度在模拟区域顶部为零，故图5-c中的紊动强度的轴分量为零。因为流体的流动方向为x轴正方向，紊动强度x轴的分量峰值较大，而y轴与z轴分量峰值接近。

图5-d中为相对平均雷诺应力τR=-＜u'w'＞/u2

*沿z轴方向的分布。在计算区域上部，流体所受到的粘性应力相比于雷诺应力可以忽略，故雷诺应力应成线性分布，本文的模拟结果基本符合。在接近床面顶部处，泥沙从紊动中获得能量从而运动，模拟的雷诺应力形成拐点。在模拟区域底边界处，雷诺应力降为零。

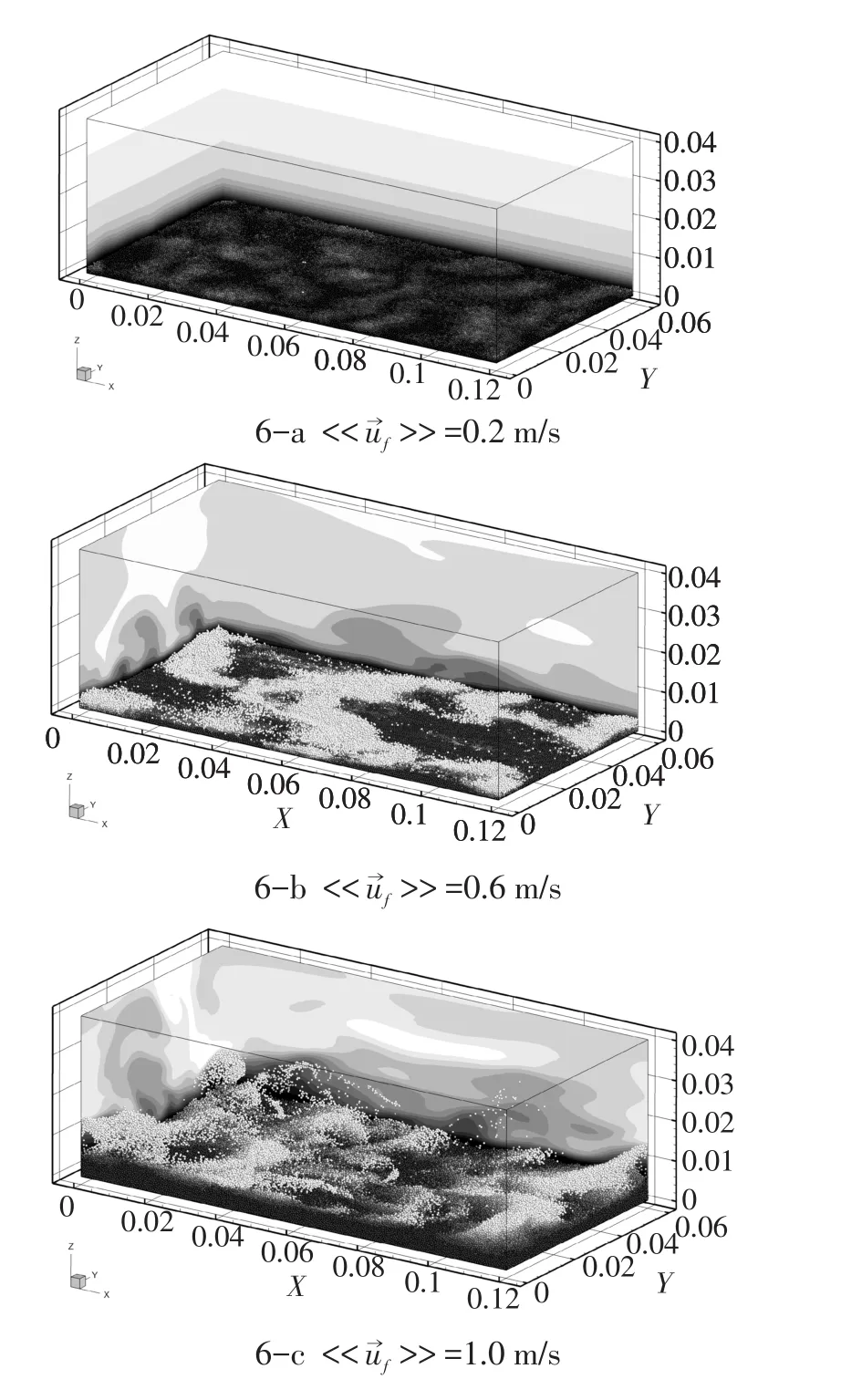
图6 模拟中三种典型的泥沙运动方式Fig.6 Three typical style of sediment transport in the simulations

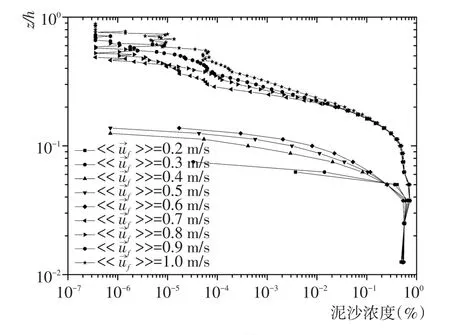
图7 泥沙浓度沿z轴方向的分布Fig.7 Profile of sediment concentration along z axis

3.2 泥沙运动分析

泥沙在不同的水流强度作用下有着不同的运动规律。选取目标流速＜＜u→f＞＞分别为0.2 m/s、0.6 m/s和1.0 m/s典型代表算例，将其流速分布与泥沙颗粒运动形式绘于图6的6-a、6-b和6-c中。从中观察得，目标流速为0.2 m/s的流场为层流状态，处于床面的泥沙均处于静止状态，此时的泥沙颗粒并未起动；目标流速为0.6 m/s的流场底部有明显的紊流结构，床面泥沙颗粒随水流沿着床面向下游运动，此时的泥沙为推移质运动；目标流速为1.0 m/s的流场紊流结构扩展至整个计算域，同时底床的泥沙有大量的起悬，泥沙为推移质与悬移质共同输沙的状态。由Shields曲线计算得到［1］，对于粒径为0.5 mm的泥沙颗粒，其起动的临界摩阻流速u*c为0.016 m/s，大于目标流速为0.2 m/s计算的摩阻流速0.012 m/s，验证了泥沙运动模拟的合理性。根据泥沙的运动形态，本文的九组算例可以分为：未起动（目标流速0.2 m/s）、推移质输沙（目标流速0.3～0.6 m/s）和推移质与悬移质共同输沙（目标流速0.7～1.0 m/s）三组。

以上三组的分组依据可以从计算区域内泥沙浓度沿z轴方向的分布中得到。图7绘制了9组算例的泥沙浓度分布图，泥沙浓度沿z轴的分布范围随着目标流速的增大而增大。图中目标流速为0.2 m/s的泥沙均集中于床面；目标流速为0.3～0.6 m/s的泥沙浓度随着z轴高度的增加而减少，此组算例的泥沙床面无量纲高度为0.042 5，大量泥沙颗粒运动的范围仅限于床面附近；目标流速为0.7～1.0 m/s的泥沙浓度分布则遍布整个z向计算范围。在接近计算域底边界处，泥沙的孔隙率为0.47，颗粒密为实堆积。对于推移质与悬移质共同输沙组，在计算域顶边界附近泥沙浓度发生振荡。产生此种浓度振荡原因为，泥沙与顶部壁面发生碰撞，运动被干扰，加之泥沙浓度较小，泥沙空间分布具有随机性。

对于推移质单宽输沙率，前人已进行过大量的实验并提出几种较为合理的计算公式。为了验证本文模拟的推移质输沙率强度，选取Gilbert、Meyer⁃Peter、Wilson及钱宁的实验值，Einstein、Meyer⁃Peter、Yalin及En⁃gelund经验计算公式［17］，与本文目标流速为0.3～0.6m/s算例的统计值进行比较。对比结果如图8所示，横轴为推移质输沙强度Φ，纵轴为Shields数Ψ（水流强度的倒数），两者的计算公式如下

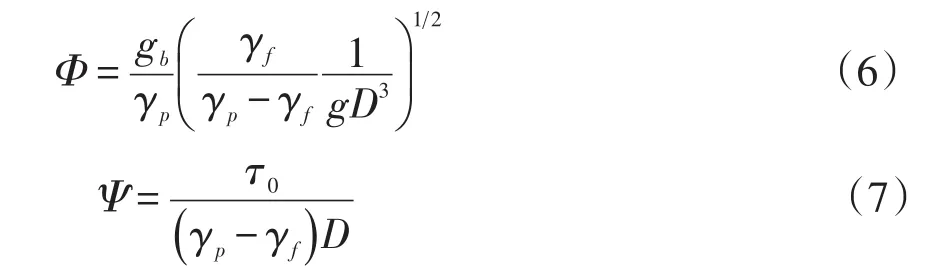
式中：gb为推移质单宽输沙率；D为泥沙粒径；γp和γf分别为颗粒和流体的重度；τ0为作用在单位床面面积上的水流拖曳力。

从图8可以看到，本文推移质输沙率的模拟值与Gilbert、Meyer⁃Peter等实验值及四种经验公式比较接近，这验证了模型对于水流作用下颗粒运动描述的合理性。

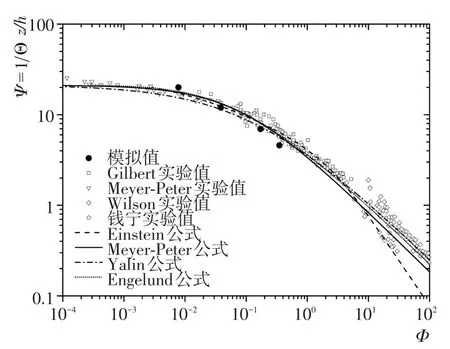
图8 推移质输沙率的模拟值、实验值与理论公式比较Fig.8 Comparison of bedload transportation among simulation result,experimental data and analytical formula

4 结论

本文采用CFD⁃DEM方法，研究了九组不同水动力条件下流体与泥沙颗粒的运动状态。模拟中，流体计算采用Smagorinsky紊流模型，颗粒接触计算采用Hertz⁃Mindlin无滑移“软球”模型，利用开源软件CFDEM耦合库进行流体-颗粒作用力的交换，完成耦合过程。从水流与颗粒运动两方面分析模拟结果得到以下结论：

（1）水流在床面附近形成明显的高低流速间隔的条带状结构，并且可以观察到紊流猝发现象，符合现有对紊流结构的认识。

（2）模拟得到的流速平均剖面符合对数律公式，保证了水动力条件的合理性。

（3）分析得到紊动强度三个方向分量与雷诺应力沿z轴的分布，紊动强度峰值出现在床面附近，接近底床和计算顶边界强度较小。计算区域上部流体的雷诺应力与理论分布接近，成线性变化。

（4）9组泥沙颗粒运动模拟中包括未起动、推移质输沙及推移质与悬移质共同输沙，平均泥沙浓度垂向分布表明了三种状态的存在。

（5）模拟得到的推移质输沙率与实验值及理论公式吻合良好。

［1］钱宁，万兆恵.泥沙运动力学［M］.北京：科学出版社，1983.

［2］王光谦，胡春宏.泥沙研究进展［M］.北京：中国水利水电出版社，2006.

［3］王光谦，孙其诚.颗粒物质及其多尺度结构统计规律［J］.工程力学，2009，26（S2）：1-7. WANG G Q，SUN Q C.Granular matter and the scaling laws［J］.Engineering Mechanics，2009，26（S2）：1-7.

［4］Zhu H P，Zhou Z Y，Yang R Y，et al.Discrete particle simulation of particulate systems：a review of major applications and findings ［J］.Chemical Engineering Science，2008，63（23）：5 728-5 770.

［5］Zhao J，Shan T.Coupled CFD⁃DEM simulation of fluid⁃particle interaction in geomechanics［J］.Powder Technology，2013，239：248-258.

［6］Ji C N，Ante M，Eldad A，et al.Numerical investigation of particle saltation in the bed⁃load regime［J］.Science China Technologi⁃cal Sciences，2014，57（8）：1 500-1 511.

［7］及春宁，刘丹青，许栋.基于颗粒离散元的沙纹演变大涡模拟研究［J］.力学学报，2015，47（4）：613-623. JI C N，LIU D Q，XU D.Large eddy simulation of sand ripple evolution using Discrete Particle Method［J］.Chinese Journal of Theo⁃retical and Applied Mechanics，2015，47（4）：613-623.

［8］Pan T W，Joseph D D，Bai R，et al.Fluidization of 1204 spheres：simulation and experiment［J］.Journal of Fluid Mechanics，2002，451：169-191.

［9］Ji C，Munjiza A，Williams J J R.A novel iterative direct⁃forcing immersed boundary method and its finite volume applications［J］. Journal of Computational Physics，2012，231（4）：1 797-1 821.

［10］乔光全，张庆河，张金凤.扁球体泥沙颗粒沉降的三维格子Boltzmann模型［J］.泥沙研究，2013（4）：1-7. QIAO G Q，ZHANG Q H，ZHANG J F.Three dimensional Lattice Boltzmann model for settling of oblate spheroid sediment parti⁃cles［J］.Journal of Sediment Research，2013（4）：1-7.

［11］Kloss C，Goniva C，Hager A，et al.Models，algorithms and validation for opensource DEM and CFD⁃DEM［J］.Progress in Computa⁃tional Fluid Dynamics，an International Journal，2012，12（2-3）：140-152.

［12］Smagorinsky J.General circulation experiments with the primitive equations：I.the basic experiment［J］.Monthly weather review，1963，91（3）：99-164.

［13］孙其诚，王光谦.颗粒物质力学导论［M］.北京：科学出版社，2009.

［14］Kline S J，Reynolds W C，Schraub F A，et al.The structure of turbulent boundary layers［J］.Journal of Fluid Mechanics，1967，30 （4）：741-773.

［15］Grass A J.Structural features of turbulent flow over smooth and rough boundaries［J］.Journal of Fluid Mechanics，1971，50（2）：233-255.

［16］建忠.湍流的拟序结构［M］.北京：机械工业出版社，1995.

［17］钱宁.推移质公式的比较［J］.水利学报，1980（4）：1-11. QIAN N.A Comparison of the Bed Load Formulas［J］.Journal of Hydraulic Engineering，1980（4）：1-11.

Simulation of fluid⁃sediment particle motion near bed based on CFD⁃DEM coupling method

SU Dong⁃sheng,ZHANG Qing⁃he,SUN Jian⁃jun,LI Ming⁃xing
（State Key Laboratory of Hydraulic Engineering Simulation and Safety,Tianjin University,Tianjin 300072,China）

Based on CFD⁃DEM method,using computational fluid dynamics software OpenFOAM,particle mo⁃tion simulation software LIGGGHTS and CFDEM coupling library,a coupled fluid⁃particle model was developed and applied in the investigation of flow and particle near bed in different hydrodynamic conditions.The simulation results show that the coupled model has a good performance on describing turbulence intensity and the distribution of Reynold stress.For particle motion,this model can also depict well the three typical states of settled,bedload transport and bedload⁃suspended load transport.The simulated results of bedload discharge per unit have a good match with experimental data and empirical formula.

CFD⁃DEM coupled model;near bed flow;turbulence intensity;bedload sediment transport

TV 142；O 242.1

A

1005-8443（2016）03-0224-07

2015-11-16；

2015-11-25

国家自然科学基金资助（51179122）

苏东升（1991-），男，陕西省宝鸡人，硕士研究生，主要从事港口海岸及近海工程研究。

Biography：SU Dong⁃sheng（1991-），male，master student.