数值模拟中海床临界冲刷切应力的计算方法

肖天葆

（1.广东茂名滨海新区管理委员会，茂名525000；2.河海大学港口海岸与近海工程学院，南京210098）

数值模拟中海床临界冲刷切应力的计算方法

肖天葆1，2

（1.广东茂名滨海新区管理委员会，茂名525000；2.河海大学港口海岸与近海工程学院，南京210098）

针对目前计算海床临界冲刷切应力公式适用性不强的问题，文章从实测资料出发，借助于波流共同作用下的泥沙数学模型，提出了一种经过验证的计算海床临界冲刷切应力的通用性方法。该方法不需要大范围的海域泥沙实测资料，其适用性相对较强，且能在一定程度上很好的保证海床临界冲刷切应力的连续性，减少人为随意的手动调试。

临界冲刷切应力；海床；数值模拟

目前，在以切应力法处理水沙界面通量的近岸泥沙运动的数值模拟中，海床临界冲刷切应力的计算是一大难点。虽然人们对此的研究比较多［1-3］，并有计算临界冲刷切应力的相应公式，且一般认为其是泥沙粒径、干密度及水深等参数的函数，如张瑞谨公式、Van Rijn公式、Nicholson和O′Connor公式等［4］。但具体到某一特定海域，若实测资料缺乏，再加上前人得出的经验公式一般适用性有限，那么在这一特定海域就不一定适用。因此，提出一种计算海床临界冲刷切应力的通用性方法显得十分必要。

本文拟根据连云港历年实测资料及悬沙遥感定量反演图，借助于波流共同作用下的泥沙数学模型，从基本理论出发，提出了一种经过验证的计算海床临界冲刷切应力的通用性方法，为泥沙运动的研究提供参考。

1 自然条件

连云港地处江苏省北部黄海海州湾西南岸，潮汐运动受制于南黄海驻波系统，为非正规半日潮型，多年平均潮差3.39 m，平均涨潮历时5 h38 min，平均落潮历时6 h48 min，由于受近岸地形影响，潮流从外海向岸边逐渐由逆时针旋转流向往复流过渡。

本海域以风浪为主，常浪为偏东北向，多年出现频率26.41%；强浪为偏北向，多年出现频率18.40%。据1962～2003年实测波浪资料统计，累年有效波高H1/3为0.4～0.6 m，累年平均波高H1/10为0.5 m。

连云港海域地处淤泥质海岸，水浅坡缓，海床泥沙中值粒径0.002～0.004 mm，干密度600～640 kg/m3，近岸多年平均含沙量0.2～0.25 kg/m3。“波浪掀沙，潮流输沙”是连云港海域泥沙运动的控制机制。

2 基本理论

海床的临界冲刷切应力是泥沙数学模型计算的重要参数，一般认为其与计算海域的泥沙特性有关。根据Sanford和Maa［5］的研究，淤泥质海床的临界冲刷切应力随海床泥沙密度垂向的增大而迅速增大，若海床冲刷1 cm，则临界冲刷切应力可增加0.8 N/m2以上。此外，庞启秀［3］在室内水槽和环形槽试验中也得出类似结论，即临界冲刷切应力随水深及泥沙密度的增大而增大，直至达到某一固定值。另据卢惠泉［6］的研究：水动力对沉积物的机械分选作用显著，使沉积物的分布具有较明显的规律性。这也就是说水动力机械分选沉积物，进而影响海床临界冲刷切应力，即海床临界冲刷切应力会随水动力的变化而变化，直至达到某一种平衡，水动力强，其相应的临界冲刷切应力也就大，水动力弱，其相应的临界冲刷切应力也就小。综上所述，可以这样认为：水动力在塑造海床的同时，也塑造了相应的临界冲刷切应力，在海床冲淤平衡的条件下，床面切应力与临界冲刷切应力正相关。

由此，提出以下计算海床临界冲刷切应力的公式

对于近岸浅水海域，有

对于外海深水海域，由于波流的掀沙作用已不明显，因此可以认为该海域海床不可冲刷，即

式中：τce表示海床临界冲刷切应力，是判定泥沙起悬的一个物理量，若τce小于床面切应力，则床面泥沙将起悬；τmax、τmean分别表示床面切应力的最大值和平均值，其值可以从数模结果中提取出来。k值表征海床冲刷的难易程度，应通过模型率定给出，其值越大，表示海床越难冲刷。一般来说，从近岸浅水海域到外海深水海域，为保证海床冲刷难易的连续性，k值应逐渐增大。

3 数学模型的建立

根据基本理论的分析，海床的临界冲刷切应力在达到某一种平衡之前是随水动力的变化而变化的，因此，若要计算出一个不随时间而变化的临界冲刷切应力场，就需要考虑水动力的平均情况，即选取代表水动力。根据解鸣晓［7］对连云港海域的研究，代表潮可选取2005年9月的实际中潮，因为该实际潮平均潮差3.82 m，高于多年平均潮差12.6%，符合Latteux［8］对代表潮的研究。由于连云港海域常浪向偏NE向，为简化模型计算，本次研究仅选取NE向为代表波向，其相应的风向取45°。

3.1 潮流基本方程

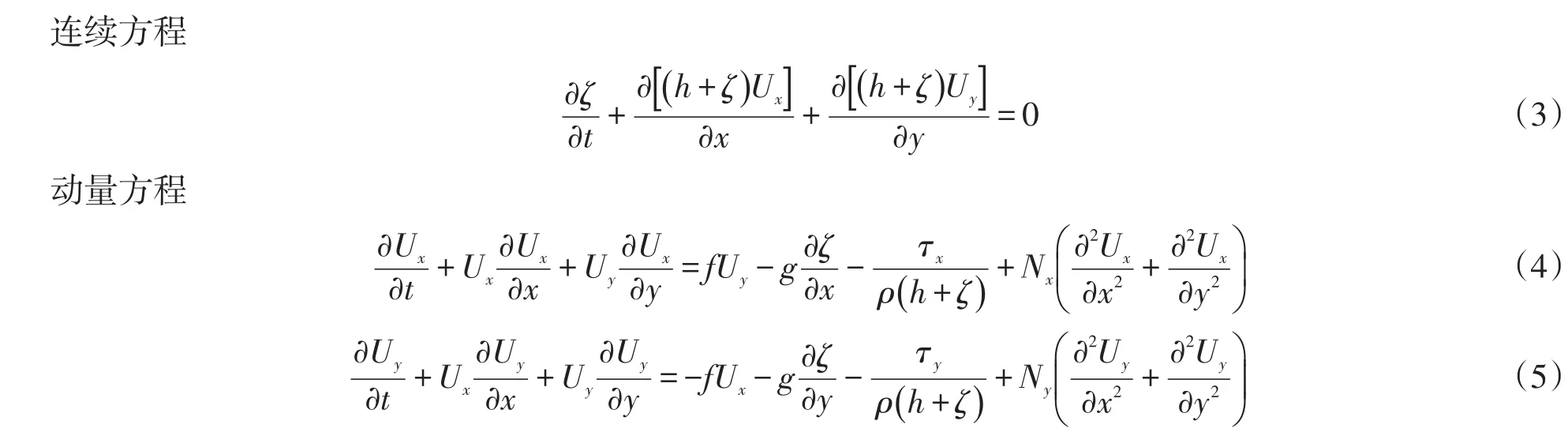
式中：x、y为直角坐标系坐标；t为时间变量；Y为平均水深；ζ为相对于平均海平面的潮位；Ux、Uy为x、y方向上的垂线平均速度；r为水流密度；g为重力加速度；Nx、Ny为x、y方向的水平紊动粘性系数；f为科氏参数（f= 2wsinf，w为地球旋转角速度，f为纬度）；τx、τy为床面剪切应力在x、y方向的分量。

3.2 波浪基本方程

在直角坐标系下，动谱平衡方程形式如下

式中：N为动谱密度；σ为相对波浪频率（当坐标系随水流运动时观测到的频率）；θ为波向，Cx、Cy、Cσ、Cθ为波浪沿x、y、σ、θ方向传播的速度。S为源汇项，如下表示

式中：Sin为风能输入项；Snl为非线性波-波相互作用的能量传输；Sds为波浪白帽耗散造成的能量损失；Sbot为波浪底部摩阻所造成的能量损失；Ssurf为波浪破碎所造成的能量损失。

3.3 泥沙基本方程

悬移质输移扩散方程

式中：S为垂线平均含沙量；Dx、Dy为x、y方向的泥沙扩散系数；Fs为底部冲淤函数。

床面冲淤方程

式中：γd为床沙干容重；ηb为海底床面的冲淤变化量。

底部冲淤函数Fs

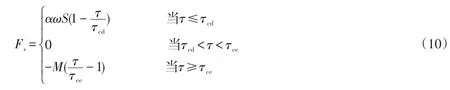
式中：τ为水流底部剪切应力；τcd为临界淤积切应力；τce为临界冲刷切应力；α为淤积概率；M为冲刷系数，kg/（m2·s）；ω为泥沙絮凝沉速。

波流共同作用下的床面剪切应力

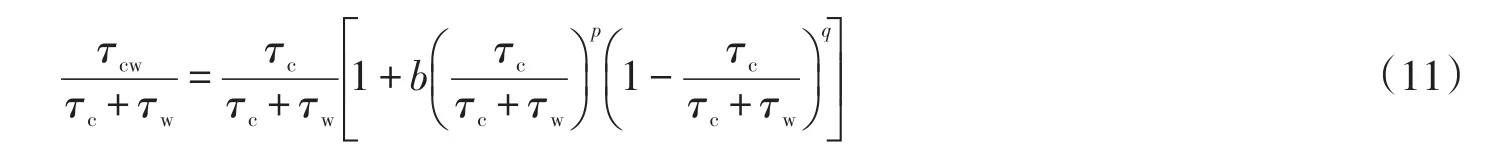
式中：τcw为波流共同作用下的切应力；τc为考虑纯流作用下的切应力；τw为考虑纯波浪作用的切应力；b、p、q为综合表达式。

3.4 网格划分、边界条件及求解方法

模型范围北起日照（35°22′30″N，119°33′E），南至废黄河口附近（34°17′00″N，120°17′E），东西宽约99.7 km，南北长约119.3 km，模型内水域面积约8 648 km2。（详见图1）由于三角形非结构网格能很好的拟合计算域的复杂边界，网格易大易小，适应地形好。因此本次研究采用三角形非结构网格对模型区域进行离散。

潮流模型的西边界、南边界为陆边界，北边界、东边界为水边界。在进行数值计算时，对于开边界，由东中国海潮波数学模型提供；对于闭边界，根据不可入原理取法向流速为0。此外，还采用了干湿判别技术进行动边界处理。

波浪模型的陆边界采用全吸收边界；灌河采用闭边界；外海开边界，通过东中国海大模型计算给出，且通过区分风浪和涌浪的形式给出（风浪与涌浪的固定分界周期取8 s）。东中国海大模型的波浪边界条件对关注区域（即连云港海域）影响甚微，可以任意选取，这里取浪透边界。

泥沙模型的水边界按实测资料及经验方法给垂线平均含沙量边界。

在对潮流方程的求解中，采用有限差分的ADI法；在对波浪方程的求解中，地理空间和谱空间离散采用单元中心有限体积法，时间离散采用分布法求解；时间步长Δt=30 s。

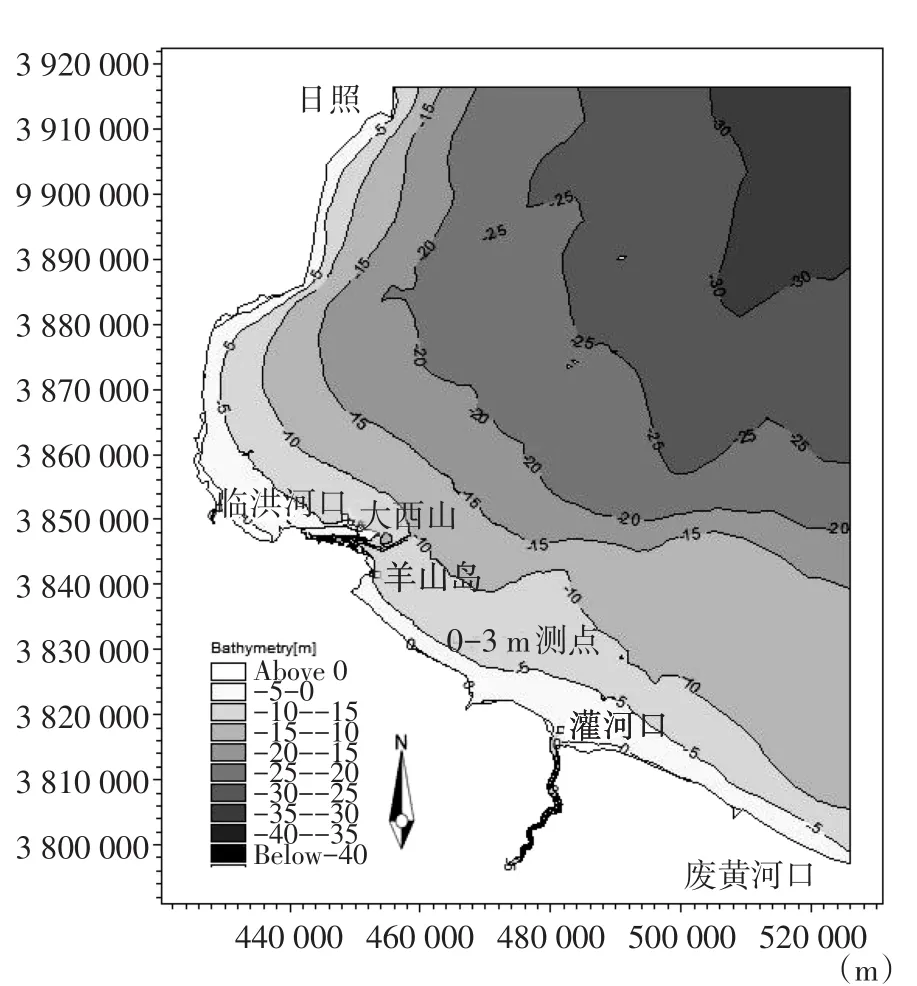
图1 连云港海域地形Fig.1 Topography in Lianyungang sea area

3.5 潮流模型的率定及验证

采用2005年9月中潮的实测潮位、流速和流向，对模型进行率定和验证，该潮型可代表多年平均情况，率定出曼宁糙率取0.012～0.016，验证结果符合规范要求［9］，限于篇幅，验证结果不列出（具体可参见文献［10］）。

3.6 波浪模型的率定及验证

由于实测资料缺乏，连云港海域仅大西山一个波浪测站。鉴于本次研究的目的，仅验证具有统计意义的常风天（NE向）代表波高、波周期及波向。验证结果（详见表1）表明：该模型计算出的波浪场可以作为代表波浪场。

表1 大西山测站常风天波浪参数验证结果Tab.1 Verification result of wave parameters of Daxishan station in common windy day

表2 大西山等测站多年平均含沙量验证Tab.2 Validation of annual average sediment concentration at Daxishan station,etc.

4 海床临界冲刷切应力的确定

本次研究在考虑海床冲淤平衡的条件下，通过对连云港海域实测多年平均含沙量及含沙量分布的验证来确定海床临界冲刷切应力。由于采用的是实测多年平均的资料进行模型验证，那么相应的所计算出来的海床临界冲刷切应力也是多年平均的情况。

在此，给出研究技术路线：通过经过验证的波流数学模型计算出床面切应力，进而统计出床面切应力的最大值和平均值，再结合公式（1）、（2），推导出初始临界冲刷切应力τce及相应的k值，并把其代入波流共同作用下的泥沙数学模型，然后进行多年平均含沙量、含沙量分布及海床冲淤平衡这三方面的反复验证，直至模型验证合理，最终率定出相应的临界冲刷切应力（详见图2）。

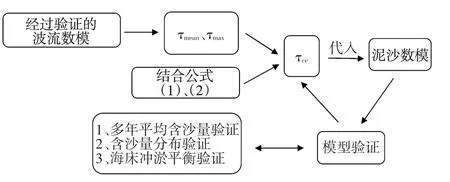
图2 技术路线图Fig.2 Technology roadmap

4.1 多年平均含沙量验证

从大西山等测站多年平均含沙量验证结果（详见表2）可知：年平均含沙量的计算值与实测值偏差未超过30%，符合规范要求［9］。

4.2 含沙量分布验证

从模型计算的年平均含沙量场（详见图3），可以看出：

（1）连云港海域含沙量分布表现为“近岸高，外海低”，高含沙水体在近岸运动，尤其在近岸破波带内，且含沙量等值线大致与等深线平行。

图3 年平均含沙量场Fig.3 Annual average sediment concentration field

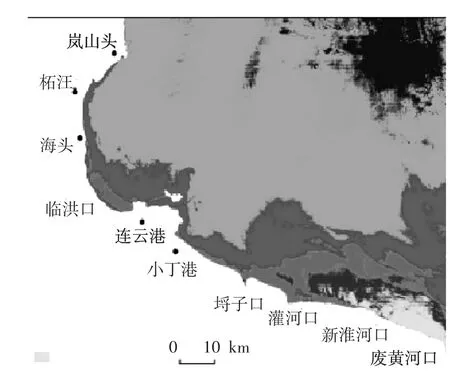
图4 表层悬沙含量分布图Fig.4 Distribution of surface suspended sediment concentration

（2）存在两个明显的高含沙量区：一个位于灌河口外，年平均含沙量在0.6～0.7 kg/m3；另一个位于临洪河口至西墅湾一带，年平均含沙量约0.3～0.5 kg/m3。

（3）模型计算出含沙量场分布形态与采用遥感技术定量反演出的2005年6月2日中潮某一时刻表层悬沙含量分布图［11］（详见图4）很相似。

以上对比说明：含沙量分布情况与以往研究成果基本一致。

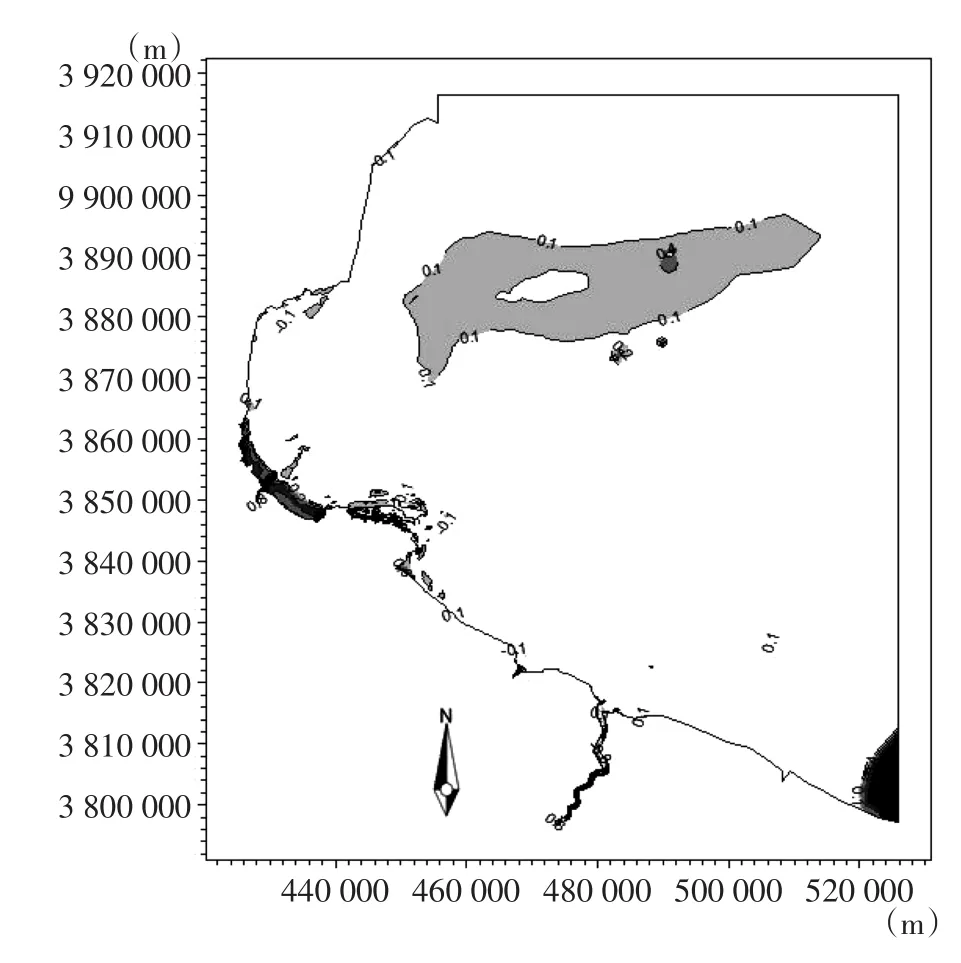
图5 海床冲淤平衡验证Fig.5 Validation of seabed erosion and deposition balance

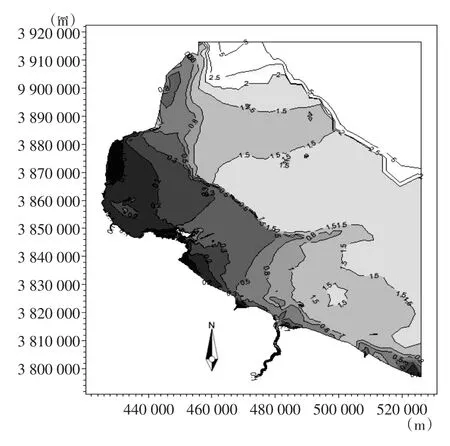
图6 海床临界冲刷切应力场Fig.6 Seabed critical shear stress field for erosion

4.3 海床冲淤平衡验证

海床冲淤平衡作为本次研究的限定性条件，但如果把其看成是模型的验证资料，那么能在一定程度上解决因实测资料缺失而引起的模型验证不准确性问题。海床冲淤平衡从理论上解释就是在一段时间内同一地点的海床冲淤相抵。从数模上表现就是最初的地形经过一段时间的冲刷与淤积后所得到的地形与最初的地形相同。因此，通过数模计算出最初的地形与最终的地形的变化即可验证海床是否冲淤平衡，其变化越小说明越接近平衡。但在自然条件中，一段时间内的海床冲淤变化基本上不可能为0，因此，可以根据海床的历年实测冲淤变化或相关经验来设定一合理数值进而衡量海床是否冲淤平衡。

从海床冲淤平衡的验证结果（详见图5），可知：除部分边界及岛屿附近，海床冲淤变化年均小于0.1 m/a，说明海床冲淤已达平衡。

4.4 临界冲刷切应力场

根据对多年平均含沙量、含沙量分布及海床冲淤平衡的验证，可知所确定的海床临界冲刷切应力场合理可信（详见图6）。该计算方法具有如下优点：一是不需要大范围的海域泥沙实测资料，其适用性相对较强。二是能在一定程度上很好的保证海床临界冲刷切应力的连续性，减少人为随意的手动调试。

5 结论

（1）基于海床垂向物理特性随冲淤变化剧烈的特征，提出了一种计算海床临界冲刷切应力的新方法：水动力在塑造海床的同时，也塑造了相应的临界冲刷切应力，在海床冲淤平衡的条件下，床面切应力与临界冲刷切应力正相关。

（2）计算海床临界冲刷切应力的新方法具有如下优点：一是不需要大范围的海域泥沙实测资料，其适用性相对较强。二是能在一定程度上很好的保证海床临界冲刷切应力的连续性，减少人为随意的手动调试。

（3）在进行泥沙模型验证时，除采用实测多年平均含沙量及含沙量分布进行验证外，还提出了采用海床冲淤平衡这一条件作为验证资料的新理论，该理论能在一定程度上解决因实测资料缺失而引起的模型验证不准确性问题。

［1］邓伯强.淤泥临界冲刷切应力研究［J］.水动力学研究与进展，1991（3）：68-75. DENG B Q.A study for critical shear stress on mud erosion［J］.Journal of Hydrodynamics，1991（3）：68-75.

［2］王虎，刘红军，王秀海.考虑渗流力的海床临界冲刷机理及计算方法［J］.水科学进展，2014（1）：115-121. WANG H，LIU H J，WANG X H.Mechanism of seabed scour and its critical condition estimation by considering seepage forces ［J］.Advances in Water Science，2014（1）：115-121.

［3］庞启秀，白玉川，杨华，等.淤泥质浅滩泥沙临界起动切应力剖面确定［J］.水科学进展，2012（2）：249-255. PANG Q X，BAI Y C，YANG H，et al.Critical stress profile for incipient sediment motion on muddy shoals［J］.Advances in Water Science，2012（2）：249-255.

［4］郑俊.近岸水沙界面通量与挟沙力关系及其应用研究［D］.南京：河海大学，2012.

［5］Sanford L P，Maa P Y.A unified erosion formulation for fine sediments［J］.Marine Geology，2001，179：9-23.

［6］卢惠泉，蔡锋，孙全.福建海坛海峡峡道动力地貌研究［J］.台湾海峡，2009（3）：417-424. LU H Q，CAI F，SUN Q.Study on the channel dynamic geomorphology of Haitan Strait，Fujian［J］.Journal of Oceanography in Tai⁃wan Strait，2009（3）：417-424.

［7］解鸣晓，张玮，张庭荣.淤泥质海岸泥沙运动模拟及进港航道大风天回淤特性研究［J］.应用基础与工程科学学报，2010（2）：262-272. XIE M X，ZHANG W，ZHANG T R.Numerical modeling of sediment transport on muddy coast and siltation feature in approach channel under the impact of strong wind［J］.Journal of Basic Science and Engineering，2010（2）：262-272.

［8］Latteux B.Techniques for long⁃term morphological simulation under tidal action［J］.Marine Geology，1995，126：129-141.

［9］JTJ/T 231-2-2010，海岸与河口潮流泥沙模拟技术规程［S］.

［10］肖天葆.连云港区不同等级航道的回淤研究［D］.南京：河海大学，2015.

［11］左书华，庞启秀，杨华，等.海州湾海域悬沙分布特征及运动规律分析［J］.山东科技大学学报（自然科学版），2013（1）：10-17. ZUO S H，PANG Q X，YANG H，et al.Analysis on the distribution and movement of suspended sediment in HaiZhou bay sea area ［J］.Journal of Shandong University of Science and Technology（Natural Science），2013（1）：10-17.

Calculation method of seabed critical shear stress for erosion in numerical simulation

XIAO Tian⁃bao1,2
（1.Guangdong Maoming Binhai New Area Administrative Committee,Maoming 525000,China;2.College of Harbor,Coastal and Offshore Engineering,Hohai University,Nanjing 210098,China）

For the present problem that the applicability of the formula of calculating the seabed critical shear stress for erosion is not strong,starting from the measured data,a proven general method of calculating the seabed critical shear stress for erosion with the help of the sediment mathematical model under wave and tidal flow was put forward in this paper.This method does not need a wide range of the observed data of marine sediment,and its appli⁃cability is relatively strong.And to some extent,this method can guarantee the continuity of the seabed critical shear stress for erosion very well and reduce artificial optional manual debugging.

critical shear stress for erosion;seabed;numerical simulation

TV 142；O 242.1

A

1005-8443（2016）03-0231-06

2015-11-02；

2015-12-14

肖天葆（1989-），男，湖南邵阳人，助理工程师，主要从事港口航道工程研究。

Biography：XIAO Tian⁃bao（1989-），male，assistant engineer.