一种有限体积悬沙输运模型在苏北辐射沙脊群海域的应用
2016-02-23孙大威
孙大威,张 鑫
(1.内蒙古民族大学,通辽028000;2河北省水运工程规划设计院,天津300074)
一种有限体积悬沙输运模型在苏北辐射沙脊群海域的应用
孙大威1,张 鑫2
(1.内蒙古民族大学,通辽028000;2河北省水运工程规划设计院,天津300074)
悬沙输运是近岸水域地形演变的重要因素之一,南黄海辐射沙脊群海域悬沙在波浪和潮流的共同作用下有着巨量的输运。文章构建了基于无结构三角形网格的Roe-MUSCL有限体积悬沙输运数值模型,其中心思想是使悬沙浓度求解过程同步且具有高分辨率。基于无结构三角形网格,将每一个独立的三角形单元作为控制个体,分别在各三角形单元上对控制方程进行Gauss线积分离散,采用二阶MUS⁃CL重构格式和Roe型数值通量形式对控制方程进行空间离散,采用一阶向前差分格式的时间离散方法,通过对扩散项的平衡处理,建立了能够适应复杂地形和水动力条件下的高分辨二维有限体积悬沙输运数学模型,并根据当地海域的悬沙浓度实测资料进行数值验证。
悬沙输运方程;有限体积法;无结构网格
数值模拟是了解悬沙输运特征的主要手段,在近海大范围开敞水域,水平尺度要远大于垂向尺度,忽略物理参数在垂向的变化,采用二维悬沙输运模型进行数值研究是可行的。
上世纪五十年代开始,泥沙数学模型的研究经了历从一维到二维再到三维,从只考虑单因素的影响到考虑多种因素共同作用,从非耦合到耦合的过程,自上世纪八十年代开始获得了迅速发展。Chang[1]等对浅水环境下等坡度海滩悬沙输运特征受波浪、潮流的影响进行了研究。窦国仁等[2]推导得出了波浪和潮流共同作用下的悬沙输运控制方程和挟沙能力公式,构建了浅水环境下的二维泥沙数学模型。Pruszak[3]等选择具有代表性的中值粒径作为研究对象,进行了示踪沙床面泥沙浓度的实验研究。Green[4]等对新西兰海岸波浪以及连续潮流对泥沙运动影响的研究。辛文杰[5]等将波浪概化为时间平均的波浪流分布场,将波浪引起的辐射应力、波流摩阻力以及波流挟沙力耦合到水流运动方程和悬沙输运方程中,得到了潮流、波浪联合作用下的二维悬沙数学模型。Eynde[6]等运用拉格朗日法所构建的二维泥沙输运模型,考虑了潮流和波浪对底部的共同作用,并对比利时海岸疏浚弃土扩散过程进行了数值模拟。
众多学者长期以来对浅水复杂水域的悬沙输运模拟研究,弱化了对精度的要求,更多体现在悬沙输运趋势方面,而本文采用的悬沙输运高精度数值方法基于无结构网格和有限体积法原理的高分辨模拟技术研究是合理且必要的。
1 悬沙输运控制方程
取笛卡尔坐标系,z轴垂直向上,XOY坐标面取未扰动静止水平面,得到垂向平均的二维悬沙输运计算控制方程

其中:悬移质泥沙水平扩散项表示为
Biography:SUN Da⁃wei(1983-),male,lecturer.

式中:u,v代表水深平均的流速在x,y方向的流速分量;H=h+s代表总水深,其中S代表水位;x,y代表平均海平面以下深度;ρx,ρy分别代表悬沙x,y方向的泥沙紊动扩散系数,C代表含沙量;Fs代表床面冲淤函数,表达式为
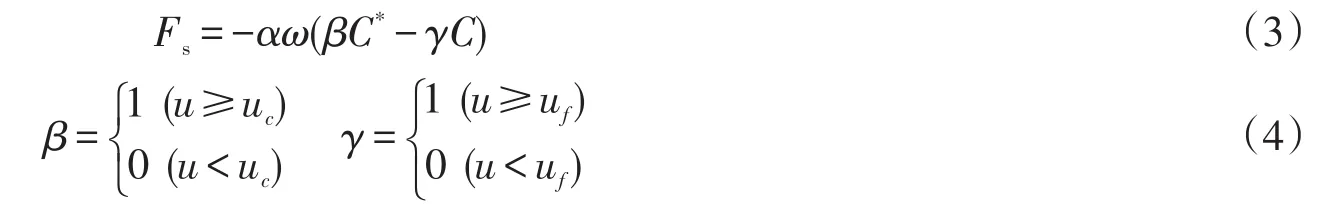
式中:ω代表泥沙沉降速度;α3代表泥沙沉降几率,通常取0.67~0.84;ω0代表水流挟沙力;uc代表泥沙起动流速;uf代表泥沙悬浮流速;p代表挟沙力恢复饱和系数;γ代表含沙量恢复饱和系数。
C*代表波、流共同作用下的挟沙力

式中:α=0.023,β=0.000 4;T代表波的周期;Hw代表波高;C2代表谢才系数,根据曼宁公式获得。
2 控制方程的离散和求解
式(1)是悬沙输运运动方程的守恒形式,改写为

令Fz=(m,n),则向量形式(6)简化为

本文选择MUSCL—TVD格式对方程进行求解
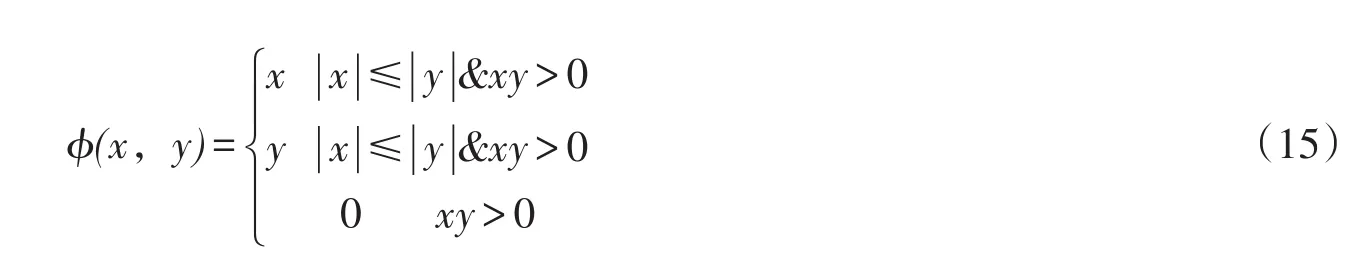
则所构造的MUSCL-TVD格式水动力计算公式如下

当线性坡度是较小值时,限制函数取Vi+1-Vi;当单元边界两侧坡度方向相反时,限制函数取0值。
时间项进行向前差分处理,
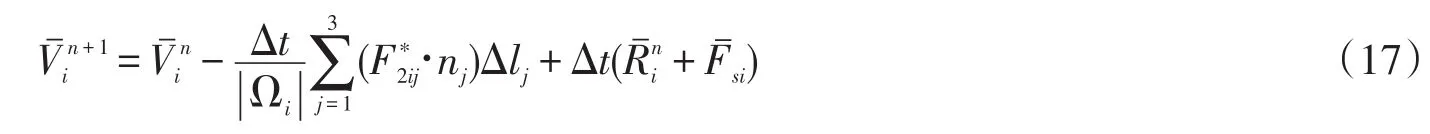
扩散项进行降阶处理的方法
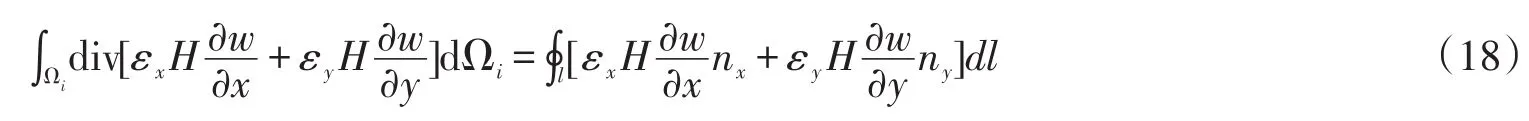
式中:w代表定义在单元形心处的任意函数值
根据格林公式得到
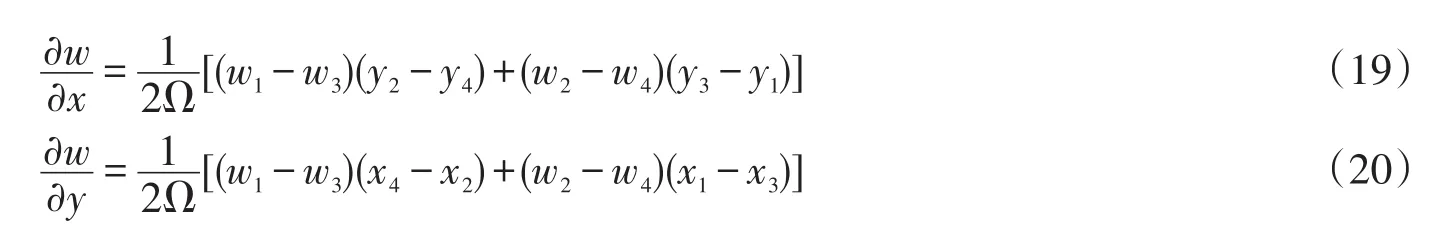
式中:Ω表示的是虚线路径包围的面积
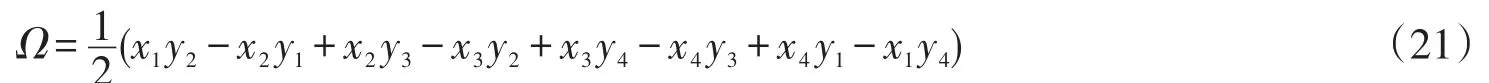
式中:xi,yi,wi(i=1,2,3,4)分别代表O1,P,O2,Q的平面坐标和w的值。计算过程中用到的控制体顶点的物理量根据文献[7]得到。
水体中的温度、盐度、悬沙浓度等调整过程较为缓慢,需要给出合理的初始场,初始场可以取自实测资料或均匀场,即
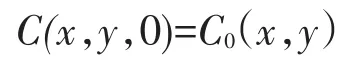
由于计算范围较大,缺少开边界潮位观测资料,本文利用中国海大范围潮波模型提供水边界条件,在边界单元处给定水位过程和悬沙浓度过程[8]
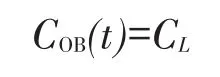
式中:COB(t)代表开边界悬沙浓度过程,当边界为入流时由Cin(x,y,t)确定;当边界为出流时由确定。固边界单元处采用镜像法:CR=CL。
3 模型应用与验证
模型的计算区域为140 km× 180 km,包括北纬31°74′~35°24′,东经119°15′~123°00′,如图2所示。为适应江苏北部海岸线不规则的特点,尽量弱化固边界对计算结果的影响,采用无结构三角形网格单元对计算区域进行剖分,如图3所示,网格边长最大尺度约400m,最小尺度约100m。
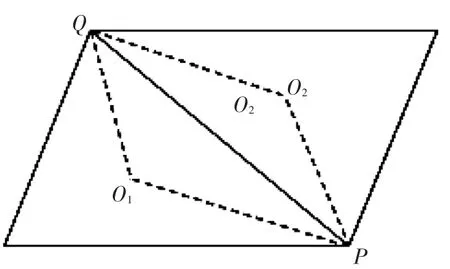
图1 积分路线示意图Fig.1 Sketch of integral path
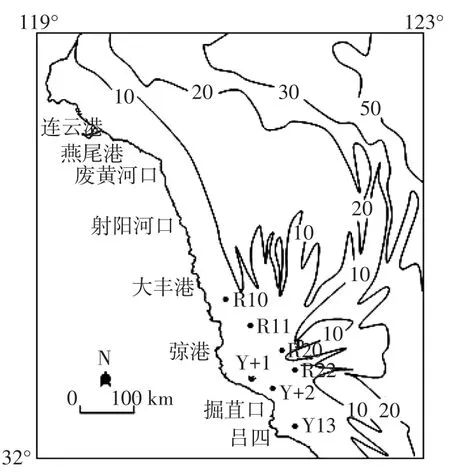
图2 水深测站示意Fig.2 Sketch of survey station
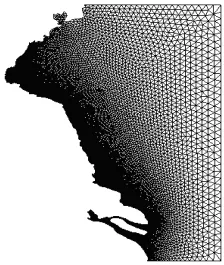
图3 计算域网格划分Fig.3 Sketch of triangle mesh
根据对此海域波况的观测统计,以NE、E、ESE向波最为频繁[9]。模型采用年最大风速下NE向2.4 m有效波高[10]为波浪场计算初始值。
水流模型以浅水方程作为控制方程,离散求解采用与本文悬沙输运模型相同的二阶MUSCL重构格式和Roe型数值通量形式,这里不再重述。
本文采用《江苏省近海海洋综合调查与评价专项》所提供的实测资料作为悬沙输运数学模型的边界条件和验证依据。悬沙浓度测站位置如图2所示。北部海州弯水域悬沙中值粒径范围在0.006~0.022 mm之间分布;废黄河口至小洋口港海域悬沙中值粒径范围在0.007~0.01 mm之间分布;洋口港以南海域悬沙中值粒径范围在0.009~0.013 mm之间分布[11]。
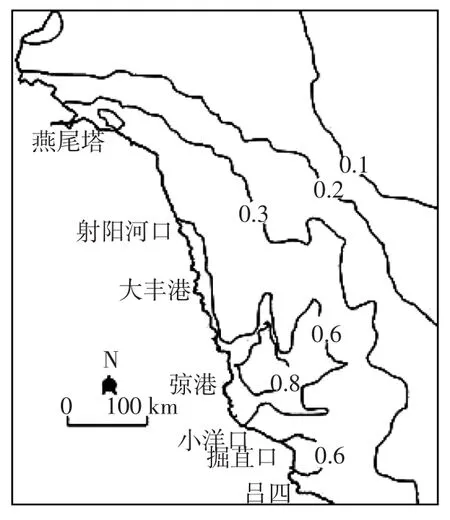
图4 大潮涨急平均含沙量Fig.4 Sediment concentration for the maximum flood during spring tide
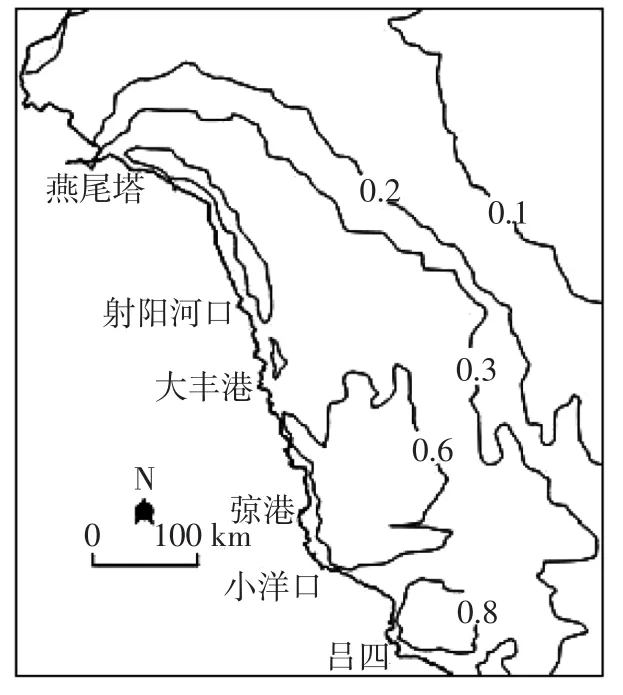
图5 大潮落急平均含沙量Fig.5 Sediment concentration for the maximum ebb during spring tide
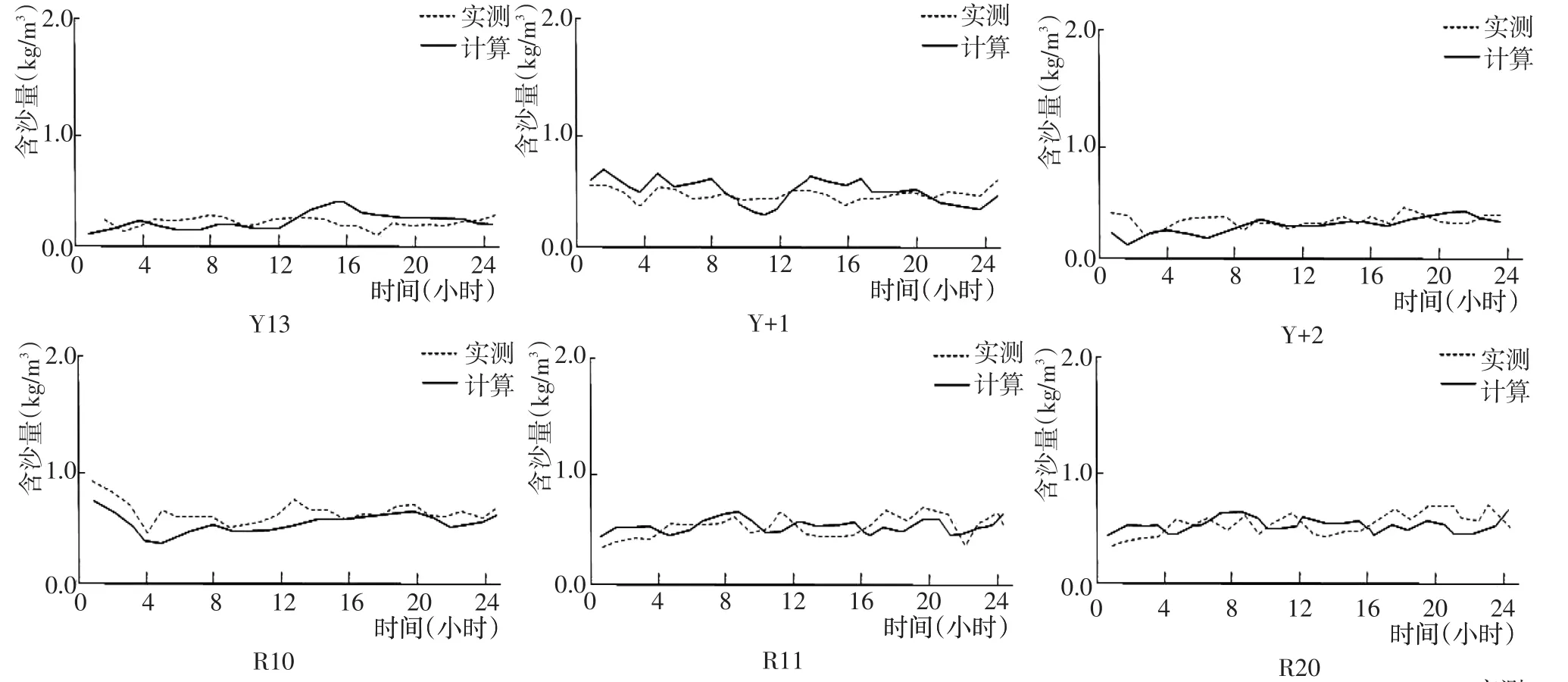
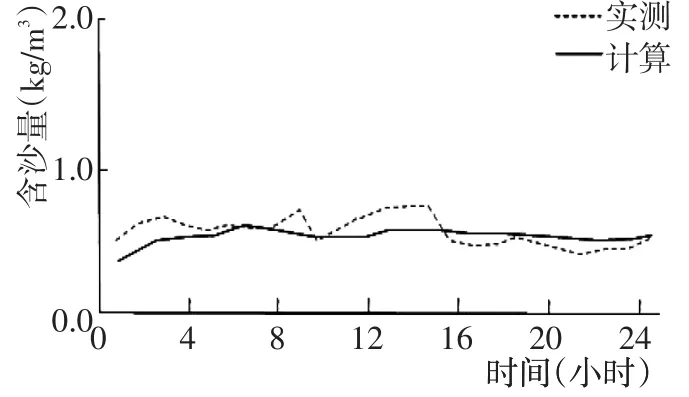
图6 大潮悬沙浓度验证Fig.6 Suspended sediment validation during spring tide
由图4、5可知,大潮水体含沙量在辐射沙脊群中心处达到最高值,随着水深的不断加大而逐渐降低,等值线分布形式与等水深线大体一致(如图2),高含沙量水体存在于沙脊群水深较浅区域。在涨潮过程中,各方向水流通过沙脊间潮流水道向沙脊群交汇处集中;在落潮过程中,由沙脊群顶点向外呈辐散状流动。该海域水动力强劲,泥沙易于悬浮,形成了高含沙量水域分布特征。随着水深的不断加大,水体的挟沙能力逐渐下降,在此过程中外围海域水体中的悬移质沙体逐渐落淤,含沙量也随之下降,形成了与等水深线分布相似的含沙量等值线,这与文献[8]的分析结果相近。
由于验证数据有限,故大潮时对7个观测点进行验证,悬沙浓度验证图6表明,悬沙浓度的模拟值同实测值的分布趋势基本相同。
辐射沙脊群海域含沙量等值线与水深等值线分布相似,水体含沙浓度随着水深的减小而变大,在沙脊群中心处达到极大值。涨潮过程中水流由各方向潮流通道汇聚于此,落潮时沿着相反方向分散,所以辐射沙脊群海域的流场具有辐射状特征。由于泥沙在强劲流场作用下呈悬移质状态,是造成此区域水体的高含沙量的原因。水体协沙能力随着水深的增加而变弱,在外围海域逐渐落淤,形成推移质,故水体含沙量变小,形成了与水深等值线相似的含沙量等值线分布。
4 结论
本文构建了基于无结构三角形网格的Roe-MUSCL有限体积悬沙数值模型,其中心思想是使水动力求解与悬沙浓度求解过程同步且具有高分辨率。基于无结构三角形网格,将每一个独立的三角形单元作为控制个体,分别在各三角形单元上对控制方程进行Gauss线积分离散,采用二阶MUSCL重构格式和Roe型数值通量形式对控制方程进行空间离散,采用一阶向前差分格式的时间离散方法,建立了能够适应复杂地形和水动力条件下的高分辨二维有限体积悬沙数学模型。
对江苏北部辐射沙脊群海域进行了悬沙数值模拟,通过对计算结果和观测数据的比较,表明该模型能较好地模拟各测站的悬沙浓度过程,对复杂地形具有很好的适应性。
[1]窦国仁,董凤舞,窦希萍,等.河口海岸泥沙数学模型研究[J].中国科学(A辑),1995,25(9):995-1 001.
[2]Green Malcolm O.,Black Kerry P.And Amos Carl L.Control of estuarine sediment dynamics by interactions between currents and waves at.Several scales[J].Marine Geology,1997,20(1):24-32.
[3]辛文杰.潮流、波浪综合作用下河口二维悬沙数学模型[J].海洋工程,1997,15(1):30-47. XIN W J.Numerical Model of 2D Estuarial Suspended Sediment Motion Under the Interaction of Tide Flow and Waves[J].The Ocean Engineering,1997(1):30-47.
[4]李绍武,郑建军.回流区水流运动二维模拟[J].港工技术,2006(4):8-11. LI S W,ZHENG J J.2D Numerical Modeling for Circulation in a Flume with Dead Zone[J].Port Enginering Technology,2006 (4):8-11.
[5]杨耀中.南黄海辐射沙脊群悬沙通量数值研究[D].南京:河海大学,2010.
[6]任美锷.江苏海岸带和海涂资源综合调查报告[M].北京:海洋出版社,1986.
[7]王颖.黄海陆架辐射沙脊群[M].北京:中国环境科学出版社,2002.
[8]杨耀中.南黄海辐射沙脊群悬沙通量数值研究[D].南京:河海大学,2010.
[9]任美锷.江苏海岸带和海涂资源综合调查报告[M].北京:海洋出版社,1986.
[10]王颖.黄海陆架辐射沙脊群[M].北京:中国环境科学出版社,2002.
A sediment transport numerical model with finite volume method using in the radial sand ridge field of South Yellow Sea
SUN Da⁃wei1,ZHANG Xin2
(1.Inner Mongolia University for the Nationalities,Tongliao 028000,China;2.Hebei Port and Waterway Engineering Planning and Designing Institute,Tianjin 300074,China)
Suspended sediment transport is an important factor for the evolution of the offshore area.A large amount of suspended sediment is transported under the wave and current action in the radial sand ridge field of the South Yellow Sea.Based on triangular grid,each single triangle element was seemed as the control volume to make Gauss line integral and discrete process.By the format of second order MUSCL Reconstruction and Roe flux,the space discretization of the governing equations was made.With the method of time discretization which based on the format of one⁃order forward difference and the equilibrium treatments of diffusion term,the two⁃dimensional water and sediment mathematical model with finite volume and high precision was established for complex terrain and hy⁃drodynamic condition,and the water flow of the radial sand ridge field in the northern part of Jiangsu province was numerically simulated.
suspended sediment transport equation;finite volume method;unstructured mesh
TV 139.16
A
1005-8443(2016)03-0237-05
2015-08-10;
2015-08-28
内蒙古民族大学博士科研启动基金资助项目(BS325)
孙大威(1983-),男,辽宁省盖县人,讲师,主要从事浅水环境水动力数值模拟研究。
