巧用数形结合思想 完善学生数学认知

李德江

摘 要：进入中学之后，数学知识的理论性、抽象性逐渐增强，而此时学生的感性思维仍占主体思维，不少学生在学习的过程中往往会感觉到晦涩、难懂，导致学生的数学学习兴趣较低、学习积极性不高，严重制约了数学教学活动的有效开展。教学中就需要教师能够巧用数形结合思想，通过公式与图形的有机结合、通过数字与实践的充分理解来完善学生的数学认知能力，引导学生进行有效的数学知识学习。

关键词：数学；数形结合；学生；认知；培养

中图分类号：G632 文献标识码：B 文章编号：1002-7661（2016）03-194-01

“完全平方公式”要求学生会推导完全平方公式，并能运用公式进行简单的运算，形成推理能力；利用多项式与多项式的乘法以及幂的意义，推导出完全平方公式，掌握完全平方公式的计算方法；培养学生观察、类比、发现的能力，体验数学活动充满着探索性和创造性。教学中就需要教师能够巧用教学引导，通过有效的数形结合、知识联系来丰富学生的学习体验，运用课下的实践运用来巩固学生的学习成果。

一、巧用问题引入，激发学生学习兴趣

都说“好的开端是成功的一半”，在教学的过程中也是如此：良好的教学引导能够更好的激发学生的学习兴趣、提升学生的学习积极性。中学数学知识理论性强、对于学生的学习自主性、理解能力都有较高的要求。教学中就需要教师能够巧用教学引导，激发学生的学习兴趣。例如在“完全平方公式”教学中教师就可以运用小学时期的“两位数乘法”来引导学生进行计算：从最简单的15×15、25×25到95×95，让学生进行计算。不少学生在计算的过程中仍然采用简单的竖式乘法，计算速度相对较慢。教师在教学中就可以直接说出答案，让学生进行验算，以此来激发学生的求知欲望。此时教师就可以引入“完全平方公式”：（a+b）2=a2+2ab+b2。根据这个公式，15×15其实就是（10+5）×（10+5），即152=（10+5）2=102+2×10×5+52=100+100+25=225.同样的道理，教师还可以引入（a-b）2=a2-2ab+b2：即152=（20-5）2=202-2×20×5+52=400-200+25=225.按照这样的公式，95×95就可以进行简便运算：952=（100-5）2=1002-2×100×5+52=10000-1000+25=9025.通过小学时期知识的融入运用，不仅能够激发学生的学习兴趣，还能够降低学生的学习难度，加深学生的学习感知。

二、善用数形结合，丰富学生学习体验

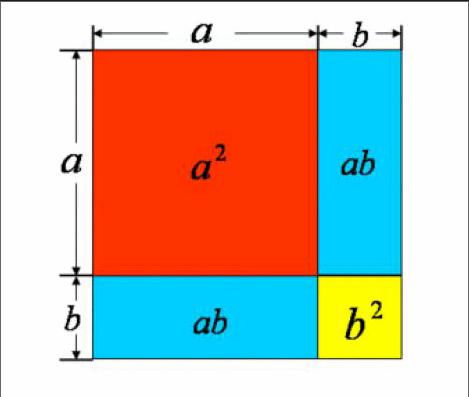
在上面的课堂导入中，完全平方是作为一个公式进行运用，进而提升计算效率的。传统教学中教师只是简单的引导学生进行公式的背诵，死记，而对于公式的原理很少对学生进行讲述，学生只“知其然而不知其所以然”，导致不少学生对于公式（a+b）2=a2+2ab+b2、（a-b）2=a2-2ab+b2的原理不了解，只是简单的背口诀，这就容易学生在运用的时候混淆。教学中教师就可以运用数形结合的教学策略来丰富教学内容（如图），教师就可以引导学生通过正方形、长方形面积的计算来引导学生进行公式的推导，通过图形的展示来引导学生进行公式的理解与记忆，让学生能够感受到知识的形成过程，进而丰富学生的学习经验、提升课堂教学的趣味性。通过图中的标示，学生能够明确的认识到边长为（a+b）的正方形面积是由边长为a的正方形、边长为b的正方形以及2个长宽分别为a/b的长方形组成的，这就为（a+b）2=a2+2ab+b2这一公式提供了直观的图形演示，很好的加深了学生的学习感知，丰富了学生的学习体验。

三、注重知识联系，完善学生数学认知

数学是一个规律性较强的学科，知识点之间相互联系、相互影响。教学中就需要教师能够注重对于学生知识体系构建的引导。因为学习的过程是一个学生自身认知能力不断提升、思维技能不断丰富的过程，教学中就需要教师能够不断的丰富教学策略，加深学生的学习认识。教学中教师也要善于运用知识之间的相互转换、知识之间的规律来引导学生进行相关内容的总结与归纳。比如在教学完全平方公式转换的时候，教师也可以采用相似的教学策略，引导学生通过图形的观察来了解相关的公式特点：例如（a+b）2其实是4个ab面积加上（a-b）2的面积组成的，即（a+b）2=（a-b）2+4ab，反过来讲就可以得到（a-b）2=（a+b）2-4ab，还可以得到（a+b）2-（a-b）2=4ab，通过图形的演示，学生能够简单明了的知道这些原理，进而更好的提升学生的学习积极性，让学生的数学知识学习显得更为趣味多彩、更加容易理解。

此外教师还可以例举相关的应用题让学生进行计算、探究，通过学生学生的实践、运用来巩固他们的学习成果，丰富学生的学习体验。例如已知实数a、b满足（a+b）2=10，ab=1。求下列各式的值：（1）a2+b2；（2）（a-b）2。

分析：此例是典型的整式求值问题，若按常规思维把a、b的值分别求出来，非常困难；仔细探究易把这些条件同完全平方公式结合起来，运用完全平方公式的变形式很容易找到解决问题的途径。

解答：（1）原式=（a+b）2-2ab=10-2=8。

（2）原式=a2-2ab+b2=（a+b）2-4ab=10-4=6。

四、做好课下运用，巩固学生学习成果

我们知道，作业是检验学生学习成果的重要形式，也是引导学生进行课下复习的基本手段，传统教学中的“题海式”作业很大程度上的抹杀了学生的学习兴趣，导致学生对于数学学习的恐惧、反感。在新时期就需要教师能够从学生的学习兴趣入手，从学生的生活经验入手，善于引导学生通过数学学习进行生活问题的解决，通过生活问题的解决加深学生的学习印象，实现作业的真正价值。例如教学之后教师就可以引导学生计算99992。这些在没有接触完全平方公式的时候是一个巨大的计算项目，而在学习了完全平方公式之后，我们就能够简便的进行计算，甚至是999992、9999992，我们同样可以简便进行计算。此外教学中教师还可以引导学生通过小组之间的交流、小组之间的总结，更好的丰富学生的学习经历，巩固学生的学习基础。让学生能够在相互交流中丰富自己的学习认知、在给其他同学讲解的过程中完善自身的语言组织能力与知识体系构建。

总之，数学教学中需要我们尊重学生的学习主体地位，认识到学生的认知基础，不断丰富教学模式、不断改进教学策略，引导学生全面发展、健康成长。