基于随机投影的快速稀疏表示人体动作识别方法
2016-02-16吴建宁徐海东王佳境
吴建宁 徐海东 王佳境 凌 雲
(福建师范大学数学与计算机科学学院,福州 350007)
基于随机投影的快速稀疏表示人体动作识别方法
吴建宁*徐海东 王佳境 凌 雲
(福建师范大学数学与计算机科学学院,福州 350007)
为有效解决体域网人体行为动作远程识别系统低功耗和快速准确识别的问题,提出一种基于随机投影的快速稀疏表示人体行为动作识别的方法。该方法基于压缩感知随机投影方式压缩数据,获取待测试样本邻近类中较少最近邻训练样本,构建测试样本稀疏表示时的训练样本集,以期达到最优线性重构测试样本;在降低传感器装置功耗和稀疏表示识别算法计算复杂度基础上,捕捉人体行为动作本质特征信息,提高多类别动作识别率。采用国际公开可穿戴传感器动作识别数据库WARD多类别动作数据,验证所提算法的有效性。实验结果表明,当数据压缩率为50%,所提算法能够获得最高平均识别率(92.78%),比传统稀疏表示分类算法获得的动作识别率提高近5%,并显著降低其相应的运行时间,能准确稀疏表示多类别人体行为动作信号,有效降低稀疏表示分类算法的计算法复杂度和运行时间,明显提高多类别动作识别率,为构建快速稀疏表示动作识别提供一个新的思路和方法。
体域网;随机投影;稀疏表示;邻近类;动作识别
引言
基于体域网远程监测人体活动状况,对于远程诊断、治疗、评价人体步态及健康状态变化具有重要意义[1]。快速、准确识别人体动作变化是基于体域网远程监测人体活动的关键技术,也是目前相关研究的重要内容,其基本思路主要是通过可穿戴传感器装置采集人体运动信号,并通过互联网将其传送至远端数据处理中心进行分析及鉴别。如何有效降低传感器装置功耗和快速准确识别人体动作是当前相关研究的热点问题,目前研究大多将这两个问题分别考虑研究,未能将两者结合来综合、全面地考虑体域网远程人体活动监测系统,探寻有效的人体活动识别方法。
近年来,数据压缩方法在基于体域网远程监测人体活动研究中受到广泛关注和重视。该方法的核心思想主要是:将传感器装置采集的数据在无线传输前压缩,降低数据传输量和功耗;在远端将压缩数据重构恢复,进行分析和识别。目前,一种新的数据压缩方法——压缩感知(compressed sensing,CS)理论[2]在相关研究中受到广泛关注和应用,其基本思路主要是将人体运动信号考虑为在某一个正交空间上具有稀疏性(或可压缩性),利用随机投影压缩方法,获取远低于奈奎斯特采样频率的数据,并以较高概率重构恢复原始信号。研究发现,压缩感知随机投影方法比传统数据降维方法(如主成分分析、线性判别分析等)具有较低的计算复杂性,比较适合应用于计算和存储资源有限的传感器装置上。特别地,随机投影数据压缩方法无需获取数据任何先验知识,有助于随机选择测量矩阵和压缩重构解决方案。压缩感知应用于基于体域网远程监测人体活动研究中的另一个关键问题就是压缩重构,对于准确识别人体行为动作模式至关重要。目前,研究思路主要分两个步骤实现,首先采用压缩感知重构算法恢复原始运动信号,然后设计模式识别算法对其进行鉴别,其过程耗时,难以快速、准确识别人体行为动作模式变化[3]。如何采用压缩数据快速分类,是上述研究近年来相关领域探讨的热点问题。目前,一种基于压缩数据分类方法在图像识别、人脸识别等应用领域得到广泛重视,其基本思想主要是考虑压缩数据包含原始信号的结构信息,利用少量压缩数据作为样本数据来实现信号分类[4],其关键技术主要体现为如何准确稀疏表示数据来进行分类。
近年来,新兴的稀疏表示理论在机器学习、机器视觉和模式识别等领域得到广泛关注,为基于稀疏表示信号分类提供了理论基础。Wright等学者首次基于稀疏表示理论,提出了稀疏表示分类算法(sparse representation based classifier,SRC)[5],其基本思想是将模式识别问题转化为信号稀疏表示问题,也就是在测试样本所属类的训练样本数足够多的情况下,该类测试样本可由所属类训练样本线性组合,无需考虑其他类的样本数据。当线性组合表示系数足够稀疏时,SRC算法对数据特征空间的选取并不敏感,与传统模式识别方法(如最近邻NN、最近子空间NS、支持向量机SVM等)相比,具有较高的识别精度和鲁棒性,在生物特征识别等相关领域得到广泛应用[6-7]。近年来,一些学者尝试将稀疏表示分类算法应用于体域网人体行为动作识别中,探寻解决传感器装置低功耗、快速准确识别问题的有效方法[8-10]。诸如,文献[10]提出一种基于随机投影的动作识别方法(sparse representation classification with random projection,SRC-RP),尝试对随机投影压缩样本数据进行稀疏表示分类,以降低传感节点的能量开销和提高动作识别率。研究发现,使用所有类的训练样本稀疏表示测试样本, 计算复杂度大,并且非所属类训练样本会干扰算法的识别精度和鲁棒性。目前研究的一个关键问题就是如何寻找一个局部稀疏表示的动作模式识别算法,也就是利用测试样本少数邻近样本而非所有训练样本稀疏表示测试样本,从而降低计算复杂度,其关键点是如何寻找准确稀疏表示测试样本的少数同类别的近邻训练样本[11]。当前,基于优化过完备字典的稀疏表示分类算法在相关研究领域受到广泛关注,它旨在通过对样本训练学习,获取准确稀疏表示测试样本的过完备字典,从而解决降低计算复杂度和提高识别率的问题。Huang等提出一种基于原型表示的快速稀疏表示算法,尝试利用K-SVD算法构造一个较小且满足稀疏表示条件的过完备字典,将稀疏表示问题转化为一个l1最小化范数问题[12]。但研究发现,K-SVD算法缺乏严格的理论支撑,基于其优化算法获得的过完备字典难以准确稀疏表示测试样本,影响稀疏表示分类算法性能。陈才扣等提出了一种快速的稀疏表示分类算法,旨在解决传统SRC算法计算复杂度高的问题,其基本思路是通过K最近邻(K-nearest neighbor,KNN)算法,寻找一个较小训练样本集来稀疏表示测试样本,尝试在降低算法复杂度的基础上提高算法识别率[13]。目前相关研究仅考虑采用K最近邻方法寻找快速稀疏表示分类算法,而忽略体域网远程监测人体动作系统在低功耗基础上快速识别人体动作模式的实际解决问题的方法。
为全面、综合解决体域网远程监测人体行为动作研究中低功耗和快速准确识别的问题,本研究提出了一种基于随机投影的快速稀疏表示人体动作识别的方法(fast sparse representation classification based on random projection,FSRC-RP)。该方法的基本思路是:基于压缩感知随机投影压缩数据,构建快速稀疏表示动作模式识别算法,也就是基于随机投影压缩数据,获取待测试样本m个邻近类中的k(k≤m)个最近邻训练样本,构建测试样本稀疏表示的训练样本集,以期达到最优线性重构测试样本,从而在降低传感器装置功耗的基础上,提高动作识别率。在实验中,采用公开的可穿戴人体日常行为识别数据库WARD的多种行为动作信号,并与近年相关研究的SRC算法比较,从而验证所提算法的有效性和优越性。
1 基于随机投影的快速稀疏表示人体动作识别方法
1.1 随机投影
随机投影(random projection,RP)是一种利用随机投影矩阵实现高维数据降维的数据压缩方法,具有计算复杂度低等优点[14]。假设传感器装置(或节点)采集的人体运动信号为x∈Rn1,利用随机投影矩阵A∈Rmn,可将原始信号x投影到一个m(m≤n)维子空间中,即
(1)
式中,y∈Rm1为投影压缩数据,其计算复杂度仅为O(mn)。
在实际应用中,投影矩阵的选取对于体域网人体运动信号压缩和重构至关重要。为准确从m维测量值y中以高概率重构恢复原始信号x,投影矩阵A须满足约束等距条件(restrictedisometryproperty,RIP),即对于任意一个s-稀疏信号x,存在一个RIP常数δs∈(0,1),使得下式成立,即
(2)
式中,Λ⊂{1,…,n},且|Λ|≤s,AΛ为A中由索引Λ所指示的相关列构成的子矩阵。
为有效合理地使用体域网传感装置硬件系统的有限计算资源,选用满足RIP性质的稀疏二进制矩阵(仅含0和1元素,且每列元素1的位置可随机分布)作为随机投影矩阵进行数据压缩,为后续构建快速稀疏表示分类算法提供可靠的数据。
1.2 构建稀疏表示人体动作识别模型
假设由L个传感节点(包含一个3轴的加速度数据和2轴的陀螺仪)构建的体域网采集K类人体动作模式,若传感器节点j在t时刻采集的动作信号表示为
(3)
采集h时间的传感器节点j采集的动作信号表示为
(4)
那么,由L个传感节点采样值构成一维动作向量,表示为
(5)
由第i类动作模式对应的训练集中所有一维动作向量构成过完备字典中的一个列向量,即
(6)
式中,ni表示第i类动作模式的训练样本数目,m=5Lh。
这样,由所有K种动作类别构成的过完备字典可以表示为
(7)
式中,n=n1+n2+…+nk。
假设第i类动作样本vkt的所有训练样本可线性表示为
(8)
式中,αi=[αi1,αi2,…,αini]T∈Rni1为待识别动作样本vkt的表示系数。
考虑到vkt为未知类别动作样本,将其线性表示为所有K种动作类别构成的过完备字典,即
(9)
式中,α=[0,…0,αi1,…,αini,0,…,0]T∈Rn1为所有系数,其中非零元素应集中于测试样本所属类的训练样本Vi上。
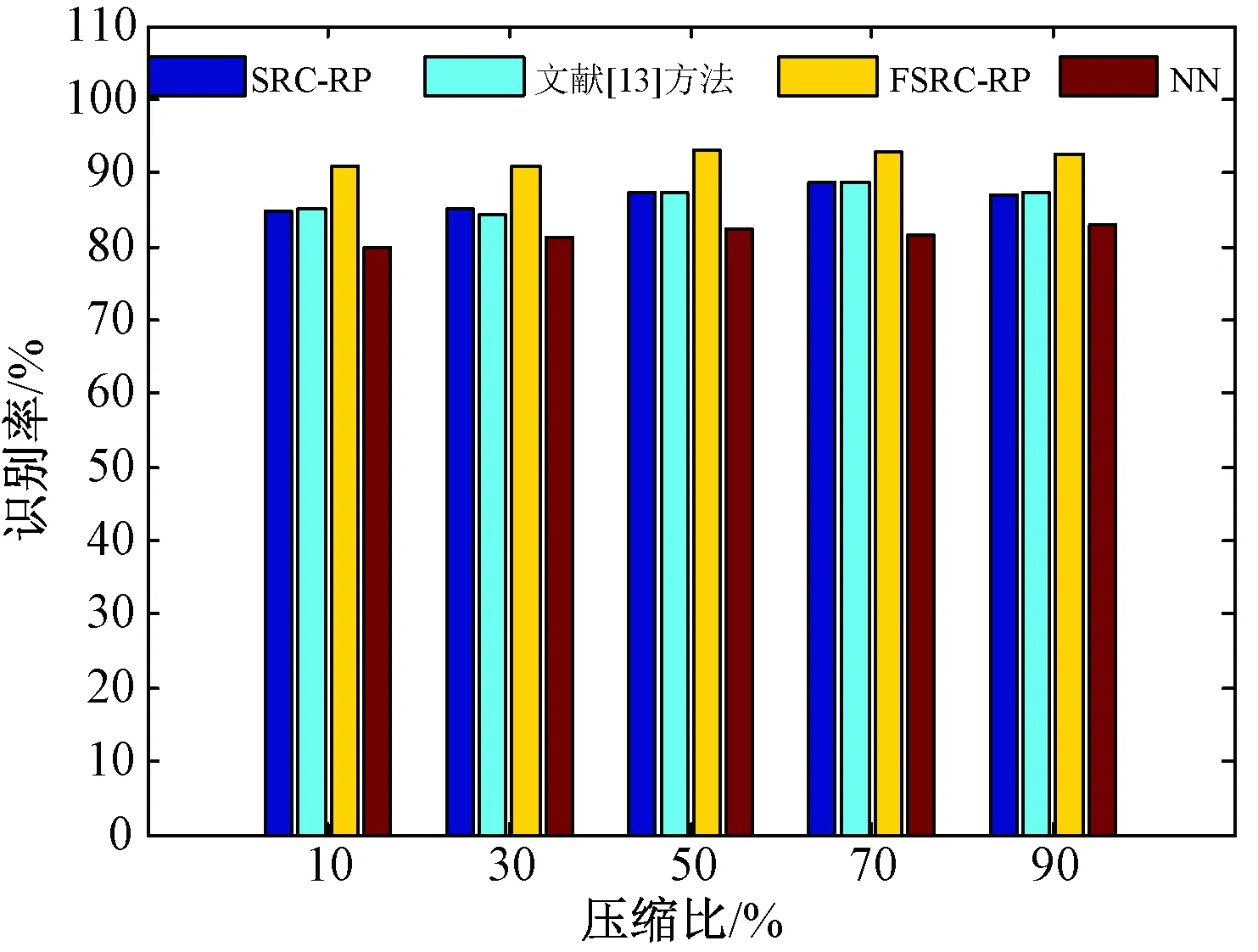
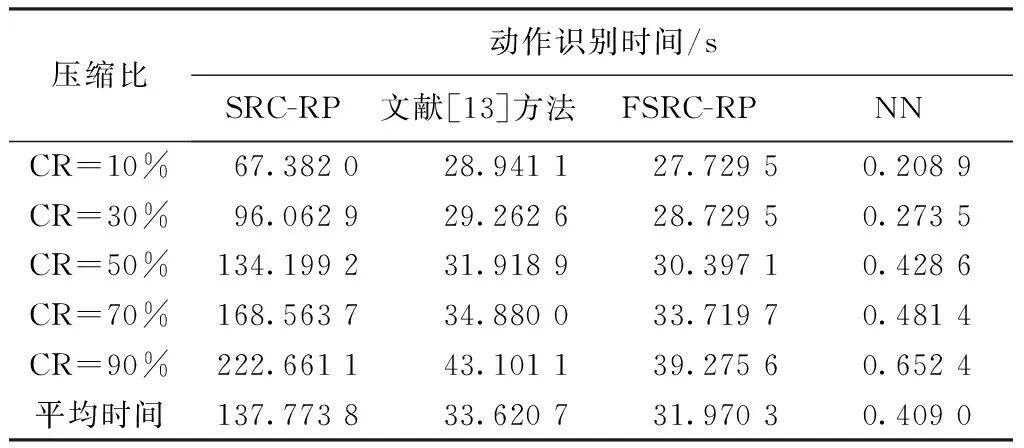
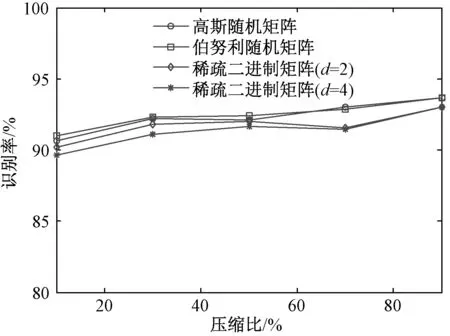
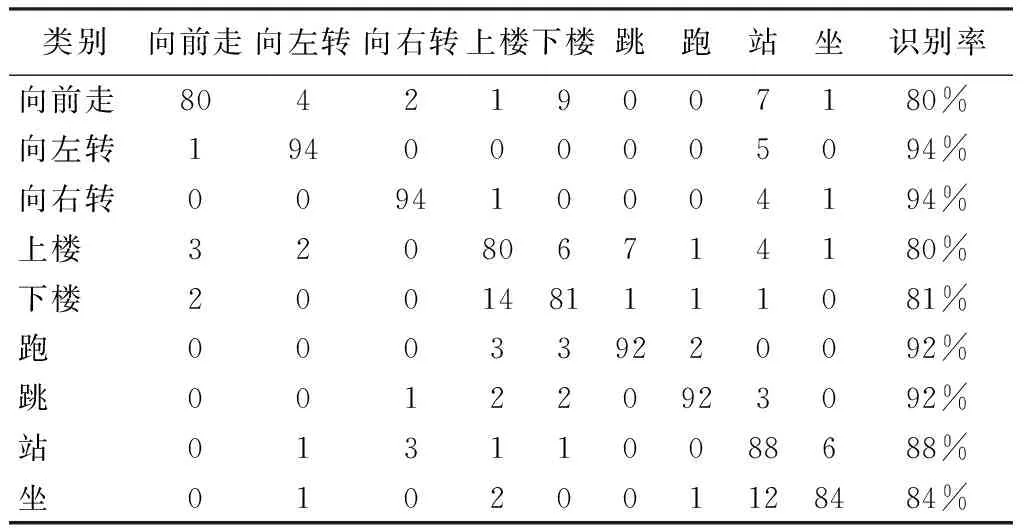
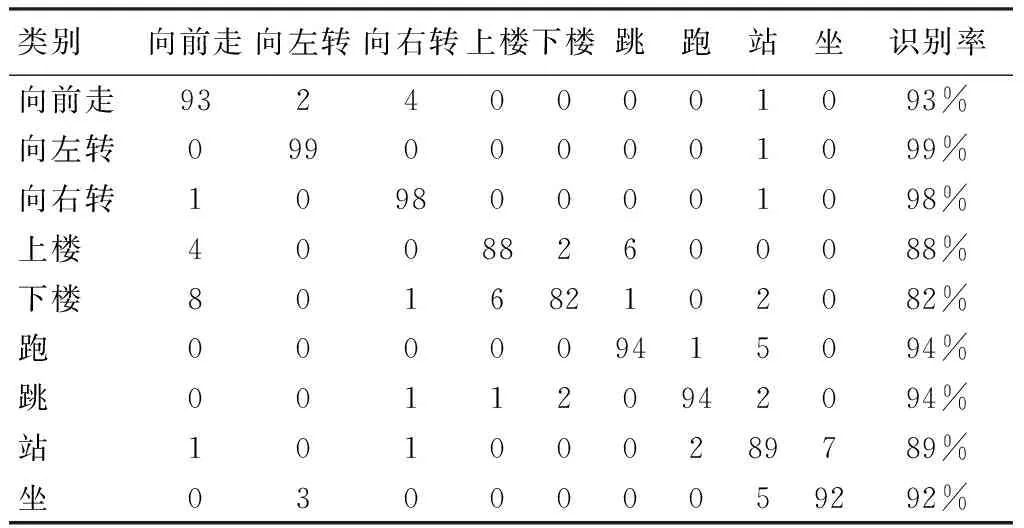
由于m (10) 上述l0最优化问题为NP问题,难以直接求解。基于动作数据的稀疏性特点,可将式(10)等价于求解下列l1最优化问题: (11) 考虑到噪声的干扰,式(9)可表示为 (12) 式中,ε为观测噪声,其稀疏表示系数的求解问题可表示为 (13) 获得稀疏表示系数后,即可根据表示系数判定待识别动作样本类别。由于稀疏表示向量的非零系数主要集中于测试样本所属类别的训练样本集中,从线性表示角度来看,较大系数对应的训练样本为所求测试样本所属的动作类别。为此,SRC算法通过计算待识别动作向量与每一类别中所有训练样本的线性加权的差值来判定测试样本所属类别,有 (14) 若差值越小,表明所属类训练样本对所选取的测试样本贡献越大,即可判定测试样本所属动作类别,有 identity(vkt)=arg minri(vkt) (15) 式中,identity(vkt)为测试样本vkt所属动作类别。 1.3 基于随机投影的快速稀疏表示分类算法 1.3.1 重新构造训练样本集 基于随机投影压缩数据构建快速稀疏表示动作识别模型的关键之处,在于寻找尽可能少的训练样本来最优线性重构测试样本。首先,在传感器节点j上,利用随机投影矩阵Aj对待识别动作向量vj,kt进行随机投影,即 (16) 在远端数据处理中心,由L个传感器节点构成的待识别动作向量为 (17) 式中,d=d1+d2+…+dL。 将矩阵A∈Rdm表示为由随机投影矩阵Aj的对角线元素构成的对角矩阵,则式(17)可表示为 (18) 同时,采用相同随机投影矩阵压缩训练样本集, 则基于随机投影的人体动作识别模型可表示为 (19) 若稀疏系数β保持足够稀疏,则可基于压缩感知理论,采用l1最小化范数问题求解。 然而,使用训练样本集中所有类的训练样本对测试样本进行稀疏表示时计算量较大,且样本集中可能包含有一些对重构测试样本贡献较小的动作类别,会降低动作识别准确率。为此,笔者假设测试样本线性表示的训练样本来自于与测试样本同类的训练样本,其他类训练样本对重构该测试样本的贡献为0。也就是说,FSRC-RP算法首先寻求其可能归属的m个邻近类别,然后利用KNN近邻方法寻找该动作向量可能归属类的k个最近邻训练样本,重新构造用于测试样本稀疏表示的训练样本集,减少不相干类别的训练样本干扰,提高动作识别的准确性,同时降低稀疏表示分类的计算开销。 1.3.2 简化KNN近邻算法 采用KNN近邻方法搜寻一个测试样本m个邻近类,即首先计算该测试样本点与所有类别的训练样本点之间的距离,然后通过比较这些距离的大小,从中找出k个训练样本点。假设xk,nn=[x1,x2,…,xk]为测试样本点对应的k个最近邻样本点,L=[l(x1),l(x2),…,l(xk)]为k个最邻近样本点对应的类别标签,通过对比k个最邻近样本的类别标签,可以确定测试样本点对应的m个邻近类别为c1,c2,…,cm。为有效降低寻找测试样本的m个邻近类的k个最近邻样本点的计算量,提出一种简化KNN近邻方法,其步骤描述如下。 步骤1:求解训练集中每类动作样本的中心样本点,有 (20) 式中,i为类序号,ni为第i类动作类别的训练样本数目。 步骤2:采用欧式距离计算测试样本、所有类的中心样本点的距离,即 (21) 式中,Cij为第i类中心样本点中第j个特征值,m为特征向量维数。 步骤3:根据步骤2计算测试样本与各类中心样本点之间的欧式距离,选出m个近邻中心样本点所对应的类别标签,即为测试样本点的m个邻近类别。 步骤4:计算第i类所有训练样本与测试样本的欧式距离,比较其大小选取其中k个最小的样本点作为该类的训练样本。重复上述步骤,直到找到测试样本m个邻近类的k个近邻样本点为止。 为此,可得到FSRC-RP算法的训练样本集为 (22) (23) 基于压缩感知理论,通过求解l1最小化范数的优化问题,可求解得到式(23)的稀疏表示系数,即 (24) 求解出稀疏系数β后,通过计算各类动作样本的重构残差,并选择残差最小的动作类别作为待识别动作向量vkt的最终识别结果。 1.3.3 本研究算法步骤 步骤1:初始训练样本集V=[v11,v12,…,vKnK],测试样本vkt,每个传感器节点的随机投影矩阵Aj,误差容忍参数,SCI阈值τ。 步骤2: 构造训练样本集和测试样本集。训练样本集:在每个传感节点上,利用随机投影矩阵Aj压缩数据;在远端数据处理中心,利用各个节点的随机投影矩阵和初始训练样本集构建训练样本集AV。基于测试样本vk,t构建测试样本Avkt。 步骤3: 将训练样本集中的每列向量归一化处理。 步骤5: 通过l1范数最小化问题求解测试样本稀疏表示系数,有 步骤6: 计算各动作类别的重构残差,有 1.4 算法验证 1.4.1 数据获取 在本研究中,选用了美国加州伯克利大学人体日常行为动作识别数据库WARD(Wearable Action Recognition Database)的人体运动数据[15]。该数据库将可穿戴多传感节点放置于人体腰部、左手腕、右手腕、左脚踝、右脚踝的解剖部位上,采集20名受试者(13名男性和7名女性)在自然状态下的13种动作数据(包括站、坐、躺、向前走、逆时针走、顺时针走、向左转、向右转、上楼、下楼、慢跑、跳、推轮椅)。每一个动作要求每名受试者重复采集5次,共采集到1 300个动作样本。其中,每个传感装置包含一个3轴的加速度计和一个2轴的陀螺仪,数据采样频率为20 Hz。选取其中常用的9种行为动作(向前走、向左转、向右转、上楼、下楼、跑、跳、站、坐)进行仿真实验。 1.4.2 数据预处理 利用滑动窗口(sliding window)方式提取数据库中的运动数据,根据数据采样频率选取滑动窗口长度为1 s,即在采样频率为20 Hz的样本中选取一段为20个采样点的运动数据作为一个动作样本。每个采样点包含一个三维加速度数据和二维陀螺仪数据,从而由5个传感器节点构成的训练样本维数m=500。 1.4.3 算法评价 为了客观、准确地评价本算法的性能,采用留一交叉验证方法评价其多类别动作识别性能,其具体方法为:将所有20名受试者的动作数据平均分成20份,依次将每名受试者的动作数据选为测试集,剩下19名受试者的动作数据作为训练集,重复上述过程,获得最终平均动作识别率。在实验仿真时,误差容忍参数选取为0.03,SCI阈值τ选取为0.4。首先测试待识别动作向量邻近类别数目对FSRC-RP算法识别性能的影响,其中稀疏二进制随机投影矩阵中每一列的非零元素个数设为2;然后比较本算法与传统最近邻NN算法、SRC-RP算法以及文献[13]的识别算法在不同压缩比下的动作识别率和识别时间,其中数据压缩比定义为 CR=d/m (25) 式中,d表示投影压缩数据的动作向量维数,m表示原始动作向量维数。 CR越大,表示原始动作向量的压缩程度就越小。此外,为进一步验证随机投影矩阵对本算法动作识别性能的影响,选择3种常用的随机矩阵(高斯随机矩阵、伯努利随机矩阵和稀疏二进制矩阵)作为本算法的随机投影矩阵。考虑到随机矩阵中元素选取的不确定性,每种随机矩阵均分别产生5次,选择5次随机矩阵的平均结果作为最终的动作识别率。通过实验仿真,根据SRC-RP算法和FSRC-RP算法在所选取数据压缩比为50%状况下的9种日常行为动作类别的混淆矩阵,验证本算法的有效性和优越性。 图1给出了数据压缩比为50%时本算法(FSRC-RP)性能随测试样本邻近类别数目的变化状况。可以看到,基于FSRC-RP算法的动作识别率随着邻近类数目的增加而增大,当邻近类数目为5时,算法识别率呈下降趋势。这可能是由于当所选取的邻近类数目较少时,测试样本所属的动作类别可能并没有被包含在所寻求的邻近类中,随着邻近 类数目的增加,算法识别率也随之上升。但当邻近类数目较大时,所寻求的邻近类中包含较多的与测试样本不相关的动作类别,导致算法识别性能下降。上述结果表明,合理选择测试样本的邻近类数目,可有效提高FSRC-RP算法的动作识别率。 图1 不同邻近类下的动作识别率变化情况Tab.1 The activity recognition rates of our method versus the variation of the training sample sizes 为验证本算法的有效性和优越性,用SRC-RP算法[8]、文献[13]的算法以及传统最近邻NN算法进行比较分析。对于本算法FSRC-RP、SRC-RP以及文献[13]方法中的动作向量稀疏系数的重构问题,采用SPGL1工具箱[16]中的基追踪去噪算法进行求解。图2给出了当邻近类数目为6、训练样本数为60时的4种分类器平均识别率随不同压缩比变化的状况。可以看到,各分类器动作识别率随数据压缩比增大而增大。当达到一定的投影维数时,各分类算法性能趋于稳定。相比而言,本算法能够获得最高平均识别率(92.78%),明显高于SRC-RP算法、文献[13]方法及NN算法动作识别率5%。结果表明,本算法能够在测试样本可能归属类的所有训练样本中,寻求k个最能稀疏表示测试样本的训练样本点,可有效降低算法计算复杂度,提高动作识别率。 图2 4种分类器在不同压缩比下的动作识别率Fig.2 The activity recognition rates of four classification algorithms on different compression rate 表1给出了上述4种分类算法在不同压缩比状况下识别9种动作类别的运行时间。从表1可以发现,基于各分类算法运行的动作识别时间均随数据压缩比的增加(也就是所要处理的动作特征向量维数越大)而增加。基于稀疏表示的动作识别方法比较而言,本算法运行的平均时间仅为31.970 3s,明显低于传统SRC-RP算法和文献[13]方法的平均运行时间,表明本算法采用较小训练样本集稀疏表示测试样本,能有效降低识别算法的计算复杂度。 表1 不同压缩比下各分类器的动作识别时间 Tab.1 The activity recognition runtime of each classification algorithms on different compression rate 压缩比动作识别时间/sSRC-RP文献[13]方法FSRC-RPNNCR=10%67.382028.941127.72950.2089CR=30%96.062929.262628.72950.2735CR=50%134.199231.918930.39710.4286CR=70%168.563734.880033.71970.4814CR=90%222.661143.101139.27560.6524平均时间137.773833.620731.97030.4090 图3 不同压缩比下不同随机投影矩阵下的动作识别率Fig.3 The activity recognition rates of different random projection matrices on different compression rate 在相同实验条件下,选取3种不同的随机投影矩阵(包括高斯随机矩阵、伯努利随机矩阵以及稀疏二进制矩阵),在不同压缩比状况下动作识别率的变化状况如图3所示。可以看到,对于不同的随机投影矩阵而言,基于本算法的动作识别率均随数据压缩比增加而增加,3种随机矩阵几乎获得相同的动作识别率。但稀疏二进制随机矩阵能够通过减少矩阵中每列非零元素的数目,进一步降低体域网传感装置计算资源和功耗[17]。上述结果表明,稀疏二进制随机矩阵有助于降低本算法的计算复杂度,提高动作识别率。 此外,表2、3分别给出基于SRC-RP算法和FSRC-RP算法在数据压缩比为50%时的9种动作类别的混淆矩阵。从结果来看,基于FSRC-RP算法可获得最优动作识别率92.11%,而基于SRC-RP算法仅获得87.22%的动作识别率,前者明显高于后者。结果表明,本算法能够充分利用随机投影矩阵,捕获不同动作的内在特征信息,有效提高了动作识别率。 表2 基于SRC-RP算法的9种动作的混淆矩阵 Tab.2 The confusion matrix of nine activities based on SRC-RP algorithm 类别向前走向左转向右转上楼下楼跳跑站坐识别率向前走804219007180%向左转194000005094%向右转009410004194%上楼320806714180%下楼2001481111081%跑000339220092%跳001220923092%站013110088688%坐0102001128484% 表3 基于FSRC-RP算法的9种动作的混淆矩阵 Tab.3 The confusion matrix of nine activities based on FSRC-RP algorithm 类别向前走向左转向右转上楼下楼跳跑站坐识别率向前走932400001093%向左转099000001099%向右转109800001098%上楼400882600088%下楼801682102082%跑000009415094%跳001120942094%站101000289789%坐030000059292% 实验结果表明,本算法能够充分基于随机投影压缩数据,寻找到尽可能少的训练样本的最优线性重构测试样本,构建快速稀疏表示动作识别模型,有效降低传感系统功耗,提高动作识别率。 基于稀疏表示构建人体动作识别模型,关键之处在于无需考虑非所属类的样本数据,选取尽可能少的所属类训练样本来线性重构测试样本。基于机器学习理论的测试样本与其相邻的某个训练样本点的类别标签一致性假设,笔者尝试寻求待识别动作向量可能归属的m个邻近类别,也就是测试样本的邻近类,然后基于邻近类的多个训练样本点稀疏表示测试样本,判定待识别动作向量所属类别。本研究与文献[11]提出的基于局部稀疏表示的分类算法不同,本算法采用待识别动作样本的邻近类而非邻近点构建的训练样本集,克服了局部稀疏表示分类算法的局限性[18]。正如图1所示,本算法能够通过所求的局部近邻样本构建的训练样本来线性重构测试样本,提高了动作识别率。此外,图1的结果与文献[13]的研究结果相似,但本算法采用不同于文献[13]的寻找m个邻近类别训练样本的选取方法。本算法既未使用邻近类的所有样本,也未使用按顺序选取的前k个样本,而是依据KNN分类算法准则,从邻近动作类别中选取最优稀疏重构测试样本的训练样本作为局部训练样本集,能够将不同类别的训练样本分别归属一个独立线性子空间中,避免各动作类别的训练样本集之间的相互干扰,有效降低测试样本因不同类别训练样本线性表示时产生的误判,提高了基于稀疏表示动作的识别算法性能,相应实验结果如图2和表2、3所示,本算法的动作识别性能明显优于传统的NN算法、SRC算法和文献[13]方法的动作识别性能。此外,本算法仅利用每个邻近类别较少的k个近邻样本稀疏表示测试样本,有效降低本算法的时间复杂度和计算复杂度,相应的实验结果如表1所示,基于本算法的动作识别时间明显低于传统SRC算法和文献[13]方法的动作识别运行时间。 从表2、3的结果发现,采用本算法能够较好识别向前走、上楼和下楼等区分度差的动作模式,这可能是由于本算法能够获得与测试样本属于同一局部子空间的k个训练样本进行线性重构,获取更本质的动作模式差异信息,有效提高动作识别算法的性能。 此外,从图3的结果可以看到,采用稀疏二进制随机矩阵,能够获得与高斯、伯努利随机矩阵几乎相同的动作识别性能。更重要的是,稀疏二进制随机矩阵能够有效控制矩阵中每列非零元素数目,有效减少传感器节点的计算资源,易于设计简单系统架构的传感器节点硬件电路系统,降低系统功耗。 在本研究中,提出了一种基于随机投影的快速稀疏表示人体动作的识别方法。该方法能够基于压缩感知随机投影矩阵压缩数据,有效降低体域网传感节点功耗,并且基于随机投影压缩数据,能有效寻找最优线性表示测试样本的较少训练样本集,构建快速稀疏表示动作识别模型,有效提高多类别动作模式识别性能,为基于体域网远程监测人体行为动作提供一个新的方法和思路。今后的工作主要是尝试基于体域网多传感数据的时空相关性,探寻在高压缩比状况下提高动作识别率的有效分类算法。 [1] 宫继兵, 王睿, 崔莉. 体域网BSN的研究进展及面临的挑战 [J]. 计算机研究与发展, 2010, 47(5): 737-753. [2]DonohoDL.Compressedsensing[J].IEEETransonInformationTheory, 2006, 52(4): 1289-1306. [3]AkimuraD,KawaharaY,AsamiT.Compressedsensingmethodforhumanactivitysensingusingmobilephoneaccelerometers[C] //IshizukaH. 2012NinthInternationalConferenceonNetworkedSensingSystems.Antwerp:IEEE, 2012: 1-4. [4]DavenportM,DuarteM,WakinM,etal.Thesmashedfilterforcompressiveclassificationandtargetrecognition[C] //ProceedingsofSPIEComputationalImagingV.SanJose:SPIE, 2007: 326-330. [5]WrightJ,YangA,GaneshA,etal.Robustfacerecognitionviasparserepresentation[J].IEEETransonPatternAnalysisandMachineIntelligence, 2009, 31(2): 210-227. [6]PilllaiJK,PatelVM,ChellappaR,etal.Secureandrobustirisrecognitionusingrandomprojectionsandsparserepresentations[J].IEEETransonPatternAnalysisandMachineIntelligence, 2011, 33(9): 1877-1893. [7]HangXiyi,WuFangxiang.Sparserepresentationforclassificationoftumorsusinggeneexpressiondata[J].JournalofBiomedicineandBiotechnology, 2009, 2009:403689. [8]ZhangMi,SawchukAA.HumanDailyactivityrecognitionwithsparserepresentationusingwearablesensors[J].IEEEJournalofBiomedicalandHealthInformatics, 2013, 17(3): 553-560. [9] 吴建宁, 伍滨. 构建基于小波熵的自训练半监督支持向量机分类模型评价老年人步态 [J]. 中国生物医学工程学报, 2013, 5(5): 588-594. [10] 肖玲, 李仁发, 罗娟. 体域网中一种基于压缩感知的人体动作识别方法 [J]. 电子与信息学报, 2013, 35(1): 119-125. [11]LiChunguang,GuoJun,ZhangHonggang.Localsparserepresentationbasedclassification[C] //The20thInternationalConferenceonPatternRecognition.Istanbul:IEEE, 2010: 649-652. [12]HuangJiabin,YangMH.Fastsparserepresentationwithprototypes[C] //IEEEconferenceonComputerVisionandPatternRecognition.SanFrancisco:IEEE, 2010: 3618-3625. [13] 陈才扣, 喻以明, 史俊. 一种快速的基于稀疏表示分类器 [J]. 南京大学学报: 自然科学版, 2012,48(1): 70-76. [14] 刘红, 刘蓉, 李书玲. 基于随机投影的加速度手势识别 [J]. 计算机应用, 2015,35(1): 189-193. [15]YangY,JafariR,ShankarS,etal.Distributedrecognitionofhumanactionsusingwearablemotionsensornetworks[J].JournalofAmbientIntelligenceandSmartEnvironments, 2009, 1(2): 1-5. [16]BergEV,FriedlanderMP.SPGL1:asolverforlarge-scalesparsereconstruction[EB/OL].http://www.cs.ubc.ca/labs/scl/spgl1, 2015-04-01/2015-08-29. [17] 吴建宁, 徐海东. 用块稀疏贝叶斯学习算法重构识别体域网步态模式 [J]. 计算机应用, 2015, 5(5): 1492-1498. [18]ChengHong,LiuZicheng,YangJie.Sparsityinducedsimilaritymeasureforlabelpropagation[C] //IEEEConferenceonComputerVision.Kyoto:IEEE, 2009: 317-324. A Fast Sparse Representation Classification Method for Human Activity Recognition Based on Random Projection Wu Jianning*Xu Haidong Wang Jiajing Ling Yun (CollegeofMathematicsandComputerScience,FujianNormalUniversity,Fuzhou350007,China) In this paper, a fast sparse representation classification method for human activity recognition based on random projection was proposed, in order to minimize the energy consumption and accurately recognize human activities from wireless body sensor networks-based telemonitoring system of human daily activity. The basic idea of the proposed method is that the random projection way of compressed sensing theory is used to reduce the amount of sampling on sensor nodes within body sensor network, and then the smaller number of nearest neighbor training samples within the neighbor classes of testing sample, which can optimally liner reconstruction testing sample, are obtained to construct the training sample set of the sparse representation of testing sample. Thus, a fast sparse representation classification algorithm with superior performance of generalization can be developed for capturing valuable features of human activity and improving the recognition rate on the basis of the lower energy consumption and computation complexity of algorithm. The multi-class activity data from international open wearable sensor action recognition database WRAD was selected to evaluate the effectiveness of our method. The experimental results showed that, when the data compression rate was 50%, the proposed algorithm could obtain the highest average recognition rate (92.78%), which was increased by approximately 5% compared with that of the traditional sparse representation classification algorithms. Meanwhile, the operating time of our proposed algorithm was significantly reduced compared with the above traditional methods.We believed that the proposed algorithm could not only effectively reduce the computational complexity and its running time but also significantly enhance the human activity recognition accuracy, providing a new idea and method for developing the fast sparse representation classification algorithm for activity recognition. body sensor network (BSN); random projection; sparse representation; neighborhood classes; activity recognition 10.3969/j.issn.0258-8021. 2016. 01.005 2015-09-16, 录用日期:2015-10-13 福建省自然科学基金(2013J01220);福建省高等学校教学改革研究专项(JAS14674);福建师范大学2014年研究生教育改革研究项目(MSY201426) R318 A 0258-8021(2016) 01-0038-09 *通信作者(Corresponding author), E-mail: jianningwu@fjnu.edu.cn
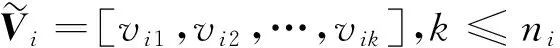

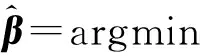
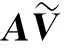
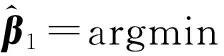
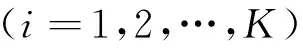
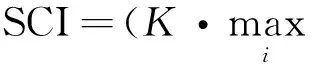
2 结果

3 讨论
4 结论
