基于滤波反投影算法的血管内光声图像重建

韩朵朵 孙 正 苑 园

(华北电力大学电子与通信工程系，河北 保定 071003)

基于滤波反投影算法的血管内光声图像重建

韩朵朵 孙 正*苑 园

(华北电力大学电子与通信工程系，河北 保定 071003)

将目前在光声断层(PAT)成像中得到广泛应用的滤波反投影(FBP)重建算法应用到血管内光声(IVPA)成像中，提出一种简单快速的二维图像重建方法。首先，对组织产生的光声信号进行滤波、逆卷积和时域一阶求导的预处理；然后，针对IVPA在血管腔内封闭成像的特殊性，采用权重法将预处理后的光声信号数据对导管以外的成像区域沿弧线进行反投影，得到成像平面内每个网格点处的初始光声压。最后，得到反映血管壁组织结构形态的横截面灰阶图像。对仿真血管模型的实验表明，采用所提出的方法重建IVPA图像的结构，相似性指标(SSIM)可达到0.571 7。合理选择滤波函数、滤波截止频率以及测量位置数，可以提高IVPA重建图像的质量；对光声信号进行时域一阶求导处理，能有效地突出重建图像中的组织结构信息。该方法为后续图像重建算法的优化奠定基础。

血管内光声成像；图像重建；滤波反投影；结构相似性

引言

生物组织光声成像(photoacoustic，PA)技术是近20年发展起来的新兴生物组织成像技术，其原理是利用不同生理状态的生物组织对光的吸收差异，激发出不同幅度的光声信号来反映组织内部结构。光声成像兼具了纯光学成像和纯超声成像的优点，可以实现高分辨力和高对比度的深度成像，已经成为当前生物医学成像研究的热点。

将光声成像技术应用于血管内部成像，即血管内光声(intravascular photoacoustic，IVPA)成像技术，可直接检测血管壁的结构与组织病变，为血管疾病的及早诊断和治疗提供可靠的依据。这种技术的原理是将微型光声成像导管插入待测血管腔内，当导管绕其轴旋转时，脉冲激光或幅度调制的连续激光均匀照射到血管壁上，激发血管壁组织产生超声信号，安置在探头顶端的超声探测器采集来自各个方向的超声回波并传送至计算机，最后重建出血管横截面的二维光吸收系数分布或者初始光声压强分布图像，获得血管的组织结构图像和几何形态信息[1]。目前，对IVPA成像的研究主要集中在成像导管和系统的实现方面[1-3]。

图像重建是光声成像必不可少的组成部分，不同类型的探测器和信号采集方式需采用不同的图像重建算法[4-6]。与扫描设备围绕成像物体旋转的光声断层(photoacoustic tomography，PAT)成像系统不同，IVPA是在封闭的血管腔内成像，其扫描孔径在血管腔内是封闭的，使光声信号数据的采集方式受到高度限制，对于这样的几何成像并不存在可靠的重建算法，只能探索应用传统方法实现图像重建的可行性和有效性[7]。目前，对IVPA成像系统的研究主要限于单阵元探测器的二维圆周扫描，适用于此类探测器的图像重建算法有滤波反投影(filtered back-projection，FBP)算法[7-9]、时间反演(time-reversal，TR)算法[10-11]和迭代重建算法[12]等，其中以FBP最为典型。

在本研究中，将目前在体外PAT图像重建中得到广泛使用的FBP算法应用到IVPA成像中，定性和定量地分析滤波函数、截止频率以及测量位置数对图像重建效果的影响，并且通过与TR算法的图像重建结果进行对比，分析FBP算法的优势与不足。

1 方法

1.1 光声成像理论

在光声成像中，由光声波动方程可得到扫描轨迹上接收到的光声信号p(r，t)[4]，有

(1)

式中，A(r)是组织的光吸收系数分布，I0是激光脉冲能量，c是生物组织中的声速，β和Cp分别是生物组织的等压膨胀系数和比热容，τ为激光脉冲宽度。

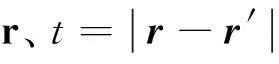
1.2 FBP算法的原理

光声成像技术利用组织激发的光声信号重建组织的光吸收分布，然而受传播过程中噪声污染和探测器自身有限带宽的影响，探测器实际检测到的光声信号并不是初始的光声信号，而是初始光声信号与探测器的脉冲响应卷积后再加上噪声的结果。因此，在进行图像重建前，必须对信号进行滤波和逆卷积处理，这对提高重建图像的质量起着重要作用。

FBP算法就是将经滤波和逆卷积处理后的光声信号沿弧线进行反投影，通过各个方向的多次叠加呈现出物体的精确位置和结构[8]。它要求投影数据必须是完备的，即探测器必须要围绕检测物体旋转360°来采集各个方向的投影数据。这种算法的优点是简单而且计算速度快，已广泛应用于单阵元探测器的体外PAT图像重建中。

1.3 基于FBP的IVPA图像重建

如图1(a)所示，IVPA的成像平面通过超声探测器并垂直于成像导管。为了简化问题，将超声探测器看作是理想的点探测器，其扫描轨迹为位于成像平面内且半径等于导管半径的圆形轨迹，成像重建区域位于扫描轨迹圆的外部。

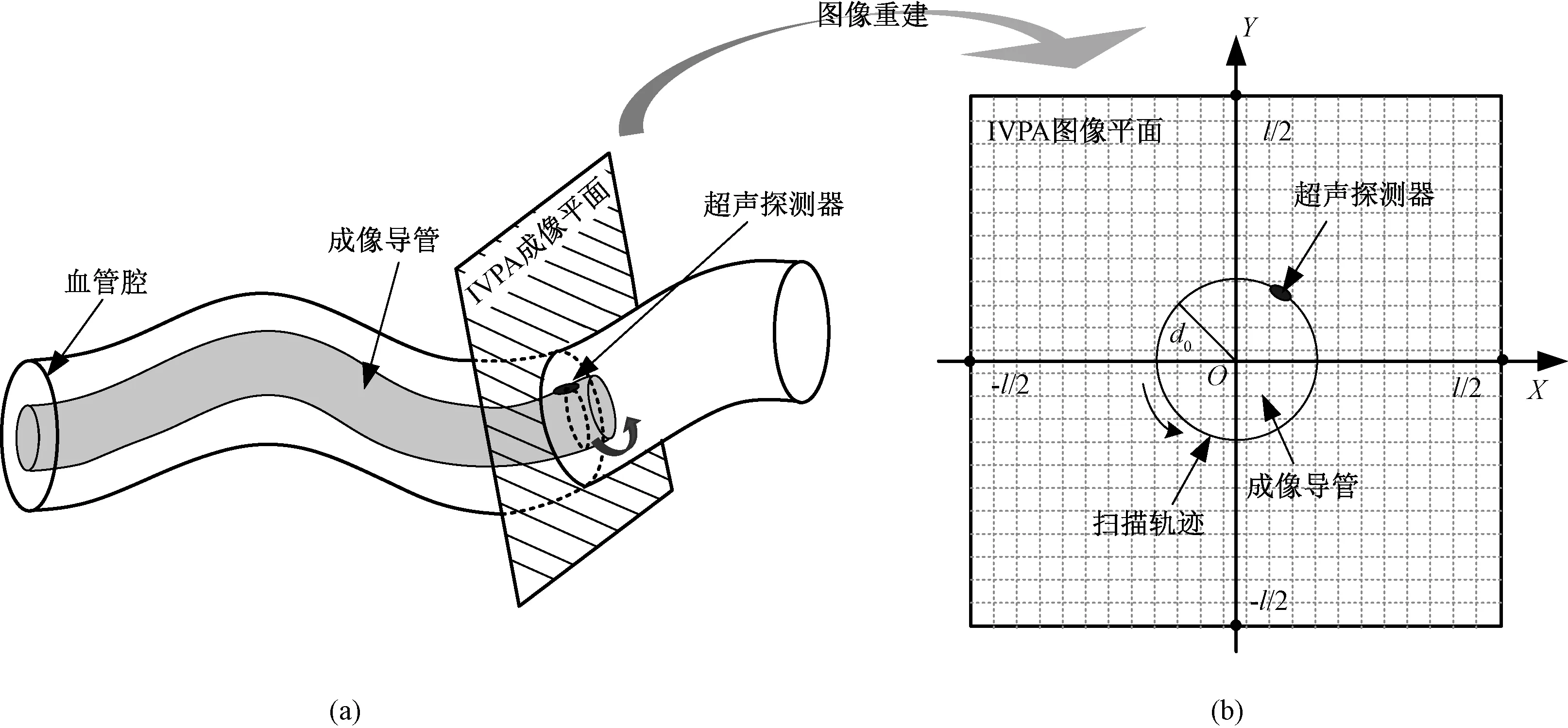
图1 IVPA图像重建。(a) IVPA成像系统；(b)初始重建图像Fig.1 IVPA image reconstruction. (a) IVPA imaging system；(b) Initial reconstruction image

结合IVPA封闭成像的特点，将FBP算法应用到IVPA图像重建中。下面对血管横截面的二维初始光声压强分布图进行重建。

1.3.1 建立初始图像

如图1(b)所示，初始图像A的宽度和高度均为l，A由M×M个正方形网格组成，第m行、第n列的网格点编号记为(m,n)，其中m=1,2,…,M，n=1,2,…,M。用M×M的矩阵B表示A，B的第m行、第n列元素的值B(m, n)是图像A中网格点(m, n)的灰度值。成像平面所在的坐标系为X-Y平面直角坐标系，其中坐标原点O是成像导管中心。

1.3.2 对采集到的光声信号进行预处理

设定成像导管在成像平面内旋转一周均匀采集K个位置的光声信号，步进角度为φ=2π/K，成像设备的采样频率为f，超声探测器的有效接收角度为θ，其在每个测量位置采集到的离散信号长度为T。用1×T的向量gi表示探测器在第i(i=1,2,…,K)个测量位置处实际采集到的光声信号。

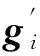
(2)

式中，Gi(ω)是gi的傅里叶变换，H(ω)是探测器的频率响应，W(ω)为滤波器的窗函数，IFFT(·)表示快速傅里叶反变换。

式(2)中的ω实际是一个简单的高通滤波函数，所以光声信号中的高频成分会被放大，进而对重建图像的质量造成严重影响，所以需要一个能抑制高频噪声的有效滤波窗函数[13-14]。

目前，常用的滤波窗函数是Ram-Lak窗函数WRL(ω)、Shepp-Logan窗函数WSL(ω)和Hanning窗函数WH(ω)[15]，定义如下：

(3)

(4)

(5)

式中，ωc表示截止频率。

用理想滤波函数|ω|乘以窗函数，即得到相应的滤波函数，分别为|ω|WRL(ω)、|ω|WSL(ω)和|ω|WH(ω)。当截止频率为5MHz时，上述3种滤波函数的频率响应曲线如图2所示。可以看出，Shepp-Logan滤波函数和Hanning滤波函数与|ω|的偏差比较大，能很好地抑制高频噪声。笔者将在本文第2节中结合实验结果，对这两种滤波函数的抗噪性能进行详细讨论。

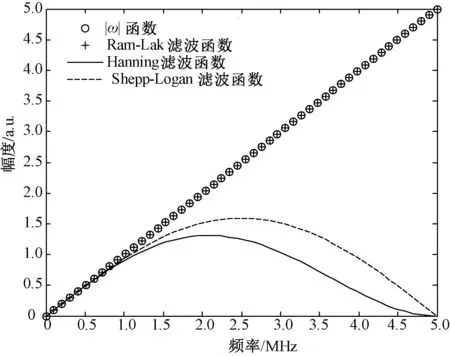
图2 3种滤波函数的频率响应曲线Fig.2 Frequency response curves of three filter functions

1.3.3 重建血管横截面的初始光声压强分布图像

图像A中的网格点(m, n)到坐标原点(即成像导管中心)的距离为

(6)

式中，dx=l/M是离散网格点之间的距离。

设成像导管的半径为d0，当r(m，n)≤d0时，说明网格点(m, n)位于成像导管内，对该类网格点不做计算。反之，当网格点在超声成像导管外部，即r(m，n)>d0时，对这些网格点继续进行以下步骤。

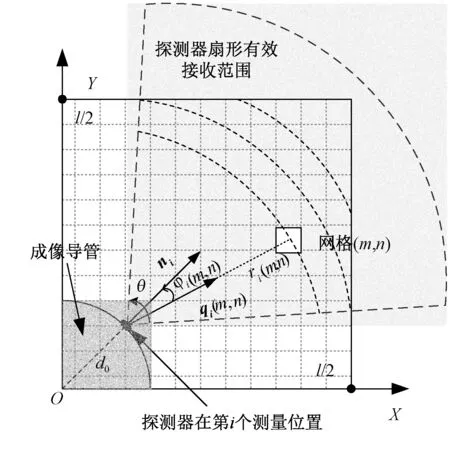
图3 IVPA反投影重建原理Fig.3 Schematic diagram of IVPA back-projection reconstruction

如图3所示，当探测器位于第i个测量位置时，其位置坐标为(d0cos(iφ),d0sin(iφ))，该点到网格点(m, n)的向量为

(7)

接收平面的法向量为

(8)

ni与qi(m,n)之间的夹角为

(9)

式中，·是向量的点积运算。

若φi(m，n)≤θ/2，说明网格点(m, n)位于以第i个测量位置为中心、圆心角为θ的扇形有效测量范围内，并且该网格点位于半径为

(10)

(11)

式中，wi(m，n)是权重因子；M×M的矩阵Di是探测器在第i个测量位置探测到的光声压强值组成的矩阵；Di(m，n)为Di的第m行、第n列元素的值，也是探测器在第i个测量位置探测到的、网格点(m, n)产生的光声压强值。

当测量位置比较密集时，相邻测量位置之间的扇形有效测量范围会发生重叠。为了避免重复计算重叠区域的网格点在不同测量位置产生的光声压强，引入权重因子wi(m，n)，有

(12)

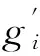
对于第i个测量位置，对图像A的M×M个网格点都进行以上计算，得到矩阵Di的所有元素值。此后，对第i+1个测量位置的采样数据重复上述操作，直至完成所有测量位置的计算，最终得到各网格点的初始光声压强值组成的M×M的矩阵D,有

(13)

式中，D(m,n)为矩阵D的第m行、第n列元素的值。

最后，将矩阵D进行归一化处理，转换为M×M维的256级灰度矩阵B，即可得到重建图像，有

(14)

式中：m=1,2,…,M；n=1,2,…,M；B(m, n)为B的第m行、第n列元素的值；Dmin和Dmax分别为D所有元素中的最小值和最大值。

1.4 算法验证

1.4.1 建立仿真模型

如图4所示，建立大小为512像素×512像素的待成像血管横截面模型，其实际高度和宽度均为4 mm，其中血管外径、管腔直径和管壁厚度分别为3、2和0.5 mm。血管壁内嵌有5个边缘清晰、规则的几何形状(椭圆形、圆形、菱形、矩形和正方形)的斑块，管壁各组织成分的颜色按照灰度条映射表示各组织成分的光吸收系数分布，灰度条数值的动态范围为20 dB。设定IVPA成像导管的直径为1 mm[3]，其中心位于图像直角坐标系的原点。

假定传播介质为理想均匀介质，声速为c=1 500 m/s，介质密度是1 000 kg/m3。超声探测器为理想的点探测器，采样频率为250 MHz，其扫描轨迹为平行于成像平面、半径等于导管半径的圆形轨迹，旋转一周共采集K个位置的光声信号数据。采用K-wave Matlab工具箱[16]，构建超声探测器在各个测量位置采集到的光声信号，再利用本算法对图4中的模拟血管横截面进行二维图像重建。

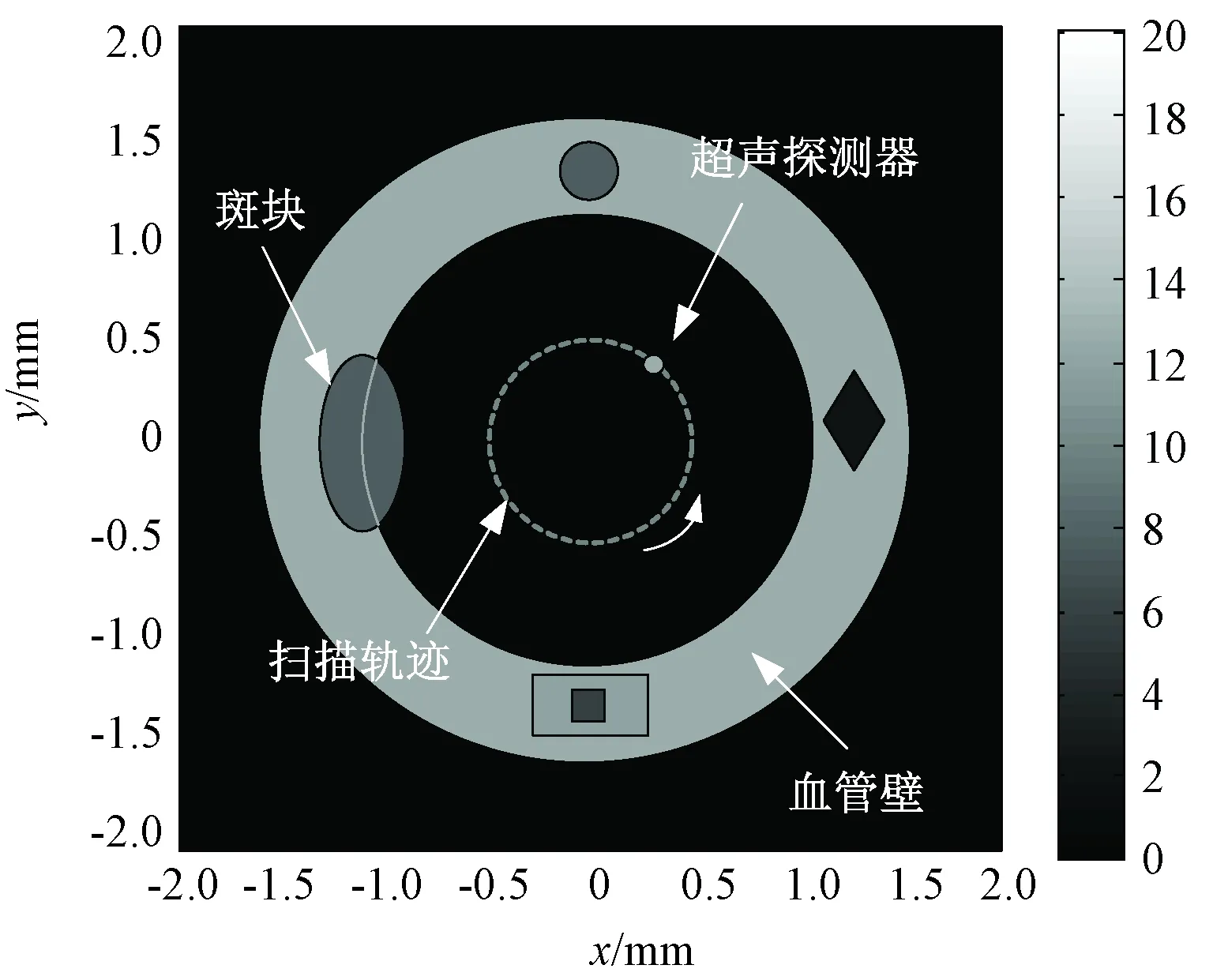
图4 血管横截面模型Fig.4 A vascular cross-sectional model

1.4.2 重建图像的定量评价指标

本研究采用基于结构相似度(structural similarity, SSIM)[17]的定量图像质量评价方法，对重建图像的质量进行客观评价。SSIM将失真建模为亮度变化、对比度变化和结构变化3个不同因素的组合，通过对上述3种变化进行相似性比较，并综合比较结果，最终得到一种评价图像质量的相似性度量指标。设标准图像和失真图像分别为X和Y，则SSIM指标可定义为

(15)

式中：μX及μY分别为标准图像和失真图像的平均亮度值；σX和σY分别为两幅图像的亮度标准差；σXY为两幅图像亮度的协方差；c1与c2是极小的正常数，用来增加计算的稳定性。

在本研究的实验中，标准图像是图4所示的血管横截面模型，那么SSIM指标值越大，说明重建图像的失真越小，当且仅当标准图像与重建图像完全一致时，其值达到最大值1。

1.4.3 时间反演重建算法

TR算法是医学图像重建中常用的方法之一[10-11]。利用TR算法重建IVPA图像时，通过建立超声传播模型，将IVPA成像扫描轨迹圆上的各个超声测量位置看作是时变的点光声信号源，并且分别依照各个位置采集到光声信号的逆时间顺序变化，在重建区域内模拟光声波传播，即可得到对原初始光声压分布的近似重建。

2 结果

在本节中，结合仿真实验结果，对滤波窗函数、滤波器的截止频率、测量位置数进行讨论，对光声信号的一阶求导预处理、对重建图像质量的影响进行分析，并与TR算法的重建结果进行对比，对本方法进行定量评价。

2.1 窗函数对重建图像质量的影响

在不同信噪比(SNR=60、20、10 dB)、截止频率为3 MHz、探测器旋转一周共采集K=360个位置的光声信号数据的条件下，分别在无滤波函数、Hanning滤波函数和Shepp-Logan滤波函数3种情况下重建图像，结果分别如图5～7所示，SSIM指标值如表1所列。从图5(a)、图6(a)和图7(a)可以看出，未进行滤波时，重建图像很模糊，血管壁的轮廓失真。由表1可见，未进行滤波的重建图像的SSIM值比经过滤波的SSIM值要小，验证了对光声信号进行滤波的必要性。分别对比图5(b)与图5(c)、图6(b)与图6(c)以及图7(b)与图7(c)，并结合表1，发现SNR=60 dB时，采用Hanning和Shepp-Logan滤波函数的SSIM值相差不大。随着噪声的逐渐增大，虽然采用两种滤波函数的重建图像的SSIM值和图像分辨率都逐渐降低，但是Hanning滤波函数的重建效果明显优于Shepp-Logan滤波函数，表明Hanning滤波函数对强噪声有较好的抑制作用，能明显提高重建图像的质量。

图5 SNR=60 dB的重建结果。(a) 无滤波重建图像；(b) Hanning滤波重建图像；(c) Shepp-Logan滤波重建图像Fig.5 Reconstructed images when SNR=60 dB. (a) Without filtering; (b) After Hanning filtering; (c) After Shepp-Logan filtering

图6 SNR=20 dB的重建结果。(a) 无滤波重建图像；(b) Hanning滤波重建图像；(c) Shepp-Logan滤波重建图像Fig.6 Reconstructed images when SNR=20 dB. (a) Without filtering; (b) After Hanning filtering; (c) After Shepp-Logan filtering

图7 SNR=10 dB的重建结果。(a) 无滤波重建图像；(b) Hanning滤波重建图像；(c) Shepp-Logan滤波重建图像Fig.7 Reconstructed images when SNR=10 dB. (a) Without filtering; (b) After Hanning filtering; (c) After Shepp-Logan filtering

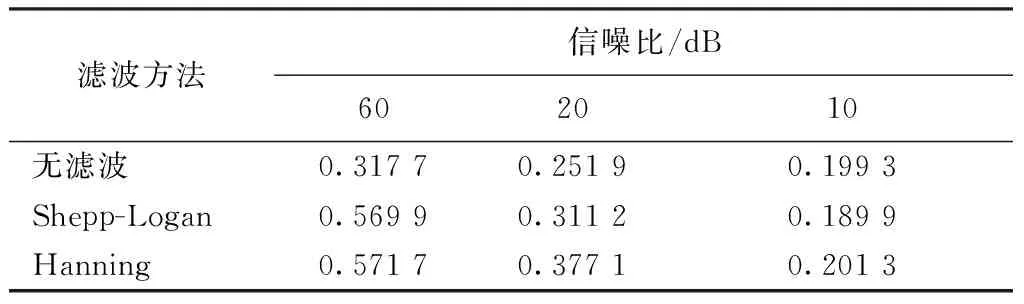
滤波方法信噪比/dB602010无滤波0.31770.25190.1993Shepp-Logan0.56990.31120.1899Hanning0.57170.37710.2013

2.2 滤波截止频率对重建图像质量的影响

选择Hanning滤波函数，在0.5～6 MHz之间以0.5 MHz为步长取值作为滤波器的截止频率ωc，采用本方法对图4所示的血管模型进行IVPA图像重建，并计算重建图像的SSIM指标值，结果如图8所示，图9是ωc分别为0.5、1.5、3、6 MHz时的重建图像。

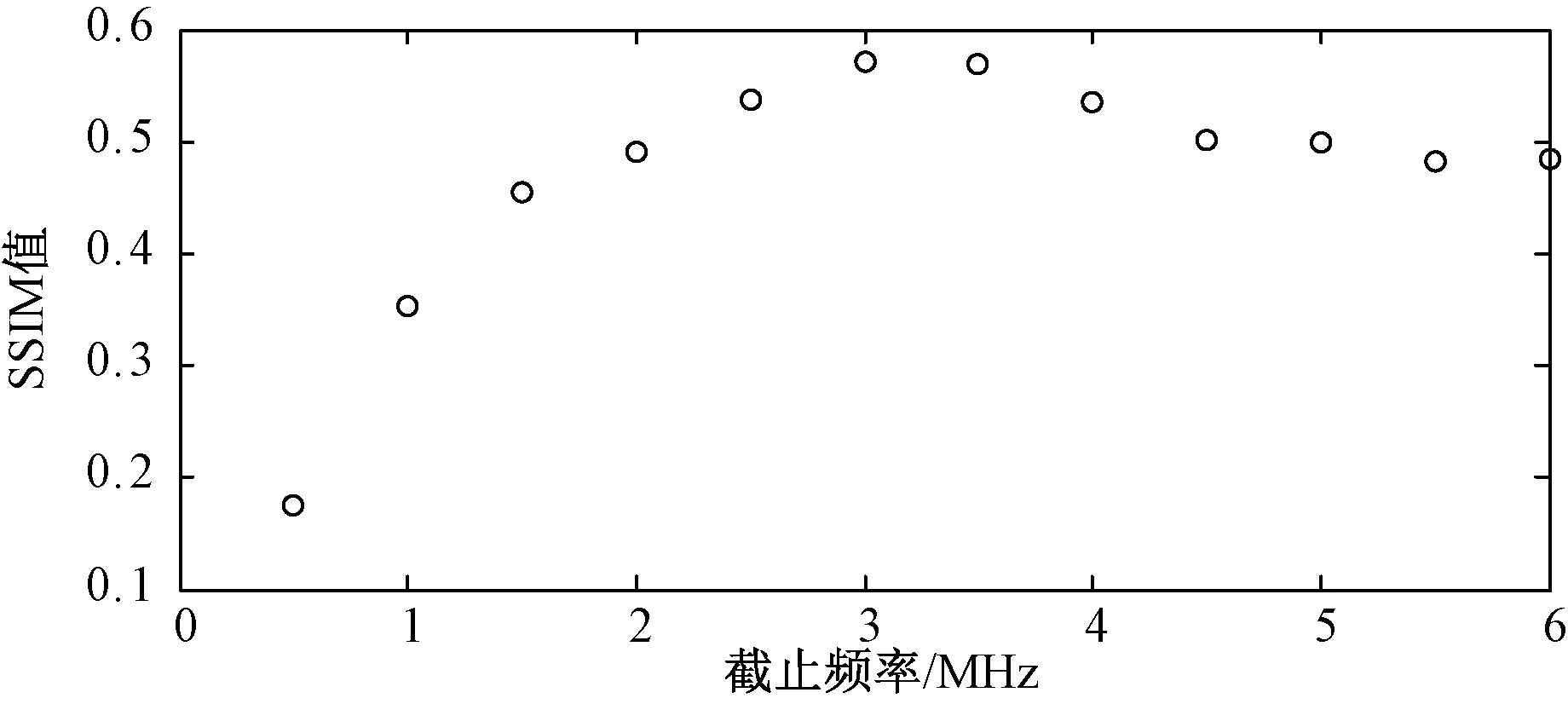
图8 采用不同截止频率的Hanning滤波函数得到的IVPA重建图像的SSIM值Fig.8 SSIM values of the reconstructed IVPA images using Hanning filters with different cut-off frequencies

由生物组织光声成像理论可知，组织产生的光声信号中的高频部分决定了成像目标细节以及边界处的成像质量。本实验采用的血管模型管壁厚度为0.5 mm，其产生的光声信号的中心频率约为2.5 MHz[18]。结合图8、9可以看出，当ωc=0.5 MHz时，重建图像的SSIM值最低；由于信号的高频成分丢失严重，图像中包含高频信息的细节和血管壁的边缘变得模糊难以辨认。随着ωc的增大，重建图像的SSIM值也逐渐升高，信号中的高频成分被放大，重建图像逐渐清晰，ωc=3 MHz时成像效果达到最好。随着ωc的继续增大，SSIM值开始下降，如图9(d)所示，图像中的血管壁边缘变得锐化，图像整体亮度降低，质量下降。上述结果说明，采用FBP算法重建IVPA图像时，图像质量对滤波器的截止频率比较敏感，需要根据实际情况进行多次实验，选择适当的截止频率，得到满意的重建图像。

图9 采用不同截止频率ωc的Hanning滤波函数得到的IVPA图像重建结果。(a) ωc=0.5 MHz；(b) ωc=1.5 MHz；(c) ωc=3 MHz；(d) ωc=6 MHzFig.9 Reconstructed IVPA images using Hanning filters with different cut-off frequencies. (a) ωc=0.5 MHz; (b) ωc=1.5 MHz; (c) ωc=3 MHz; (d) ωc=6 MHz

2.3 一阶求导预处理对重建图像质量的影响

对测量位置数分别为K=30、180和360时的仿真光声信号，分别利用原预处理方法(即仅进行滤波和逆卷积处理)和式(2)的方法进行预处理，然后再进行图像重建，其中均采用Hanning滤波窗函数，截止频率ωc=3 MHz，重建结果分别如图10、11所示，SSIM值如表2所列。对比图10、11发现，从视觉效果上来看，当测量位置数相同时，利用式(2)的预处理方法重建出的血管壁和斑块的轮廓比原预处理方法的重建结果清晰。由表2可知，除K=70时两种方法的SSIM值相近以外，在K=180和K=360时，采用式(2)的预处理方法得到的重建图像的SSIM值分别比原预处理方法得到图像的SSIM值高出10.8%和13.2%。上述结果表明，在相同测量位置数时，采用式(2)的预处理方法，可以有效提高重建图像的质量，突出成像目标的结构特征，验证了对原始光声信号进行一阶求导的必要性。

表2 不同信号预处理方法得到的重建图像的SSIM值

Tab.2 SSIM values of the reconstructed images with, respectively, the original and proposed signal preprocessing method

信号预处理方法K=70K=180K=360原始方法(滤波+逆卷积)0.35870.44480.5049本方法0.35920.49300.5717

图10 采用原信号预处理方法的IVPA图像重建结果。(a) K=70；(b) K=180；(c) K=360Fig.10 Reconstructed IVPA images with the original signal preprocessing method. (a) K=70; (b) K=180; (c) K=360

图11 采用本信号预处理方法的IVPA图像重建结果。(a) K=70；(b) K=180；(c) K=360Fig.11 Reconstructed IVPA images with the proposed signal preprocessing method. (a) K=70; (b) K=180; (c) K=360

2.4 测量位置数对重建图像质量的影响

分析图10、11和表2发现：当K=70时，由于测量位置数较少，血管壁和斑块的轮廓较模糊，且图像伪影现象严重，SSIM值也较小；当K=180时，图像的视觉效果和SSIM值都有所提高；当K=360时，SSIM值最大，成像效果最好，斑块的轮廓形状更接近原图。上述结果说明，当测量位置数较多时，能在一定程度上消除由于采集的光声数据不完备带来的伪影现象，提高重建图像质量。在实际中，受硬件设备的限制，成像导管旋转一周最多采集360个位置的光声信号，一般在此范围内测量位置数越多，则重建图像的质量越高。

2.5 与TR重建算法的对比

图12为测量位置数分别为70、180和360时的TR重建结果，其SSIM值分别为0.591 1、0.773 9和

0.864 2。对比图11、12发现，在相同测量位置数时，TR重建图像的视觉效果和SSIM指标均明显优于FBP。而且，随着测量位置数的增加，重建图像的质量也逐渐改善，在K=360时重建图像非常接近图4所示的标准图像。但是，TR算法的缺点在于其计算量大，单帧图像的重建时间过长。表3为在不同测量位置数下，分别采用FBP和TR算法重建图像所需的时间(实验所用计算机的配置为2.3 GHz Intel Core I5-2410M CPU，2G RAM)。由表3可知，FBP的重建时间随测量位置数的增加而延长，而TR算法的重建时间受测量位置数的影响很小，并且在相同测量位置数时，TR算法的重建时间约是FBP的16倍，这就限制了TR算法在实时IVPA成像中的应用。

图12 基于TR算法的IVPA图像重建结果。(a) K=70；(b) K=180；(c) K=360Fig.12 Reconstructed IVPA images based on time reversal algorithm. (a) K=70; (b) K=180; (c) K=360

Tab.3 The image reconstruction time with the FBP and time reversal algorithm

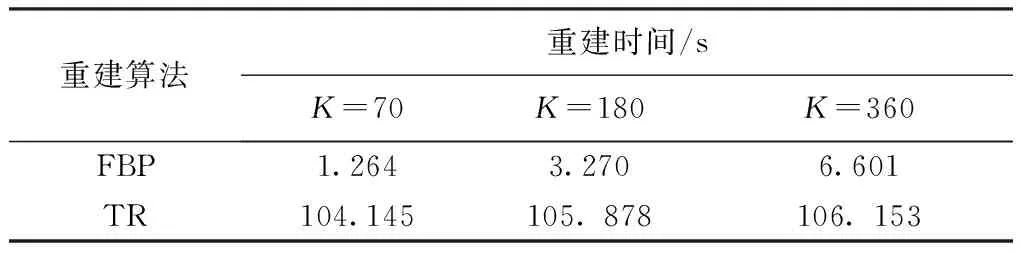
重建算法重建时间/sK=70K=180K=360FBP1.2643.2706.601TR104.145105.878106.153

3 讨论和结论

由本文第2节中的仿真实验结果可知，通过选择合适的滤波窗函数和滤波截止频率，增加测量位置数，对原始光声信号进行合理的预处理，能有效地提高重建图像的质量。但是，血管模型中的一些组织边界仍未得到有效的重建，其主要原因可归结为两方面的原因。

1) FBP算法并不是基于精确解的重建，有其固有缺陷：一是FBP算法的关键是反投影重建，而在IVPA成像中反投影是沿圆弧进行的，可能使原图像上灰度值为零的点在重建图像上的灰度值不为零，即产生伪像；二是成像对象的结构越复杂，这种现象越严重，对重建结果的影响也越大。

2) IVPA自身的成像特征局限所致。以图4中位于血管壁底部(六点方向)、相互重叠的、呈长方形和正方形的两个斑块为例，在图11(c)和图12(c)中可以看出，斑块中法线经过探测器测量位置的边界显示比较清晰，其他边界相对较模糊。这是因为对于吸收体的某一段边界，当探测器位于该边界的法线方向时，探测器测量到的这部分边界产生的光声信号达到最大；随着探测器位置逐渐偏离法线，测量到的光声信号会迅速下降。图像重建是光声信号采集的逆过程，因此在探测器位于边界的法线时边界的投影值达到最大，最易被重建出来；随着探测器位置的偏移，投影值迅速减小，重建边界变得模糊甚至不可见[19]。

另外，FBP算法的成像精度虽然不如TR算法，但其在实时成像方面具有TR算法所不能比拟的优势。采用FBP算法重建IVPA图像时，无需等待所有光声信号数据采集完毕后再进行图像重建，而是当成像导管进行机械圆周扫描时，每采集到一个位置上的光声信号，即可对其进行预处理及反投影运算。这样，可以在回撤成像导管的过程中，实时地提供血管横截面的灰阶图像。

目前，对IVPA成像的研究尚处于起步阶段，对其图像重建的研究也主要是借鉴其他比较成熟的成像技术的重建理论。本研究采用广泛应用于体外PAT图像重建的FBP算法，针对以成像导管外径为扫描轨迹的信号采集方式，在对原始光声信号进行滤波和逆卷积的基础上，增加对信号的时域一阶求导，采用权重法将预处理后的光声信号沿位于成像导管外部的重建区域内的弧线进行反投影重建，得到血管横截面的二维初始光声压分布。对仿真血管模型的实验结果表明：合理选择滤波函数、截止频率和探测器测量位置数，可以有效提高重建图像的质量；对原始光声信号进行结合了滤波、逆卷积和时域一阶求导的预处理，也能有效地提高重建图像的质量，其SSIM值可达到0.5717。与TR算法相比，FBP算法具有原理简单、成像速度快的优点，可以应用于IVPA实时成像。该方法为进一步优化IVPA图像重建算法奠定了基础，如何提高该算法的成像精度是笔者下一步的研究方向。

[1] 杨思华，袁毅，邢达. 一种血管内光声超声双模成像内窥镜装置及其成像方法 [P]. 中国专利:101912250，2012-01-04.

[2] Wang Bo, Karpiouk A, Yeager D, et al. In vivo intravascular ultrasound-guided photoacoustic imaging of lipid in plaques using an animal model of atherosclerosis [J]. Ultrasound in Medicine and Biology, 2012, 38(12):2098-2103.

[3] Bai Xiaosong, Gong Xiaojing, Hau W, et al. Intravascular optical-resolution photoacoustic tomography with a 1.1 mm diameter catheter[J]. PLoS ONE, 2014, 9(3): e92463-e92463.

[4] Xu Yuan, Feng Dazi, Wang Lihong. Exact frequency-domain reconstruction for thermoacoustic tomography-I: planar geometry [J]. IEEE Transactions on Medical Imaging, 2002, 21(7): 823-828.

[5] Xu Yuan, Xu Minghua, Wang Lihong. Exact frequency-domain reconstruction for thermoacoustic tomography-II: cylindrical geometry [J]. IEEE Transactions on Medical Imaging, 2002,21(7):829-833.

[6] Xu Minghua, Wang Lihong. Time-domain reconstruction for thermoacoustic tomography in a spherical geometry [J]. IEEE Transactions on Medical Imaging, 2002, 21(7):814-822.

[7] Sheu YL, Chou CY, Hsieh BY. Image reconstruction in intravascular photoacoustic imaging [J]. IEEE Transactions on Ultrasonics Ferroelectrics and Frequency Control, 2011, 58(10):2067-2077.

[8] Pan Xiaochuan, Anastasio MA. Minimal-scan filtered backpropagation algorithms for diffraction tomography [J]. Journal of the Optical Society of America A, 1999, 16(12): 2896-2903.

[9] Xu Minghua, Wang Lihong. Pulsed-microwave-induced thermoacoustic tomography：filtered back projection in a circular measurement configuration[J]. Medical Physics, 2002, 29(8):1661-1669.

[10] Hristova Y, Kuchment P, Nguyen LV. Reconstruction and time reversal in thermoacoustic tomography in acoustically homogeneous and in homogeneous media [J]. Inverse Problems, 2008, 24(5): 05500601-05500625.

[11] Hristova Y. Time Reversal in thermoacoustic tomography-an error estimate[J]. Inverse Problems, 2009, 25(5):55008-55021.

[12] 向良忠，邢达，谷怀民，等. 改进的同步迭代算法在光声血管成像中的应用 [J]. 物理学报, 2007, 56(7):3911-3916.

[13] 邹俊. 基于有限元的光声成像算法研究 [D]. 西安：西安电子科技大学，2012.

[14] 谭毅，邢达，杨迪武. |ω|滤波器对光声成像的影响 [J]. 激光生物学报, 2005, 15(3): 323-327.

[15] 刘晓，杨朝文. 用滤波函数的改进对卷积反投影图像重建的影响 [J]. 四川大学学报, 2004, 41(1): 112-117.

[16] Treeby BE, Cox BT. K-Wave: MATLAB toolbox for the simulation and reconstruction of photoacoustic wave fields [J]. Journal of Biomedical Optics, 2010, 15(2): 02131401-02131412.

[17] Wang Zhou, Bovik AC, Sheikh HR, et al. Image quality assessment: from error visibility to structural similarity [J]. IEEE Transactions on Image Processing, 2004, 13(4):600-612.

[18] Ku Geng, Wang Xueding, George Stoica, et al. Multiple-bandwidth photoacoustic tomography[J]. Physics Medical Biology, 2004, 49:1329-1338.

[19] Xu Yuan, Wang Lihong, Ambartsoumian G, et al. Reconstructions in limited-view thermoacoustic tomography [J]. Medical Physics, 2004, 31(4):724-733.

Reconstruction of Intravascular Photoacoustic Images Based on Filtered Back-projection Algorithm

Han Duoduo Sun Zheng*Yuan Yuan

(DepartmentofElectronicandCommunicationEngineering,NorthChinaElectricPowerUniversity,Baoding071003,Hebai,China)

A simple and fast image reconstruction method based on filtered back-projection (FBP) that has been widely applied in photoacoustic tomography (PAT) was proposed for intravascular photoacoustic (IVPA) imaging. First, the raw photoacoustic signals generated by the tissues were preprocessed by filtering, deconvolution and first-order derivation in time domain. Then, according to the specificity of IVPA scanning in the closed vascular lumen, the pre-processed photoacoustic signal data were back-projected along arcs with a weighting method to obtain the initial photoacoustic pressure of each grid point in the imaging region outside the catheter. Finally, grayscale images displaying the morphological structure of vascular cross-sections were constructed. The experimental results with a computer-simulated vessel phantom show that the structural similarity (SSIM) of the reconstructed image reached 0.5717. The image quality was improved by setting a proper filter prototype, cut-off frequency and the number of measuring positions. The structural information of the vessel wall and plaque tissues can be effectively enhanced through first-order derivation performed to the raw photoacoustic signals. This method provides the foundation for subsequent optimization of image reconstruction algorithm.

intravascular photoacoustic (IVPA) imaging; image reconstruction; filtered back-projection (FBP); structural similarity

10.3969/j.issn.0258-8021. 2016. 01.002

2015-06-01， 录用日期:2015-11-27

国家自然科学基金(61372042)；中央高校基本科研业务费专项资金(2014ZD31)

R445.9

A

0258-8021(2016) 01-0010-10

*通信作者(Corresponding author)， E-mail:sunzheng_tju@163.com