四层复杂球颅脑模型的构建
2016-02-16高彦照
柯 丽 高彦照 杜 强 韩 凌
1(沈阳工业大学生物医学与电磁工程研究所,沈阳 110870)2(东北大学中荷生物医学工程与信息学院,沈阳 110819)
四层复杂球颅脑模型的构建
柯 丽1高彦照1杜 强1韩 凌2
1(沈阳工业大学生物医学与电磁工程研究所,沈阳 110870)2(东北大学中荷生物医学工程与信息学院,沈阳 110819)
颅脑模型构建的研究是颅内成像的基础,也是磁感应断层成像(MIT)系统设计中正问题计算的必要条件。根据人体颅脑真实结构,通过Comsol Multiphysics有限元数值仿真软件的几何建模工具,构建近似真实颅脑结构的四层复杂球颅脑模型。首先,根据大脑体积和颅骨内径,构建脑实质模型;其次,根据人体解剖结构,构建颅骨模型,并进行枕骨修正、轮廓修正、额骨修正和眼眶修正;第三,通过对颅骨模型的缩放,构成头皮层、颅骨层、脊液层,并与脑实质模型共同构成具有4层结构的颅脑模型;最后,将模型置入10 MHz的交流磁场中,通过仿真计算获得头皮层、颅骨层、脊液层和脑实质层感应电流的分布,感应电流在脊液层最强,在皮肤层和脑实质层较弱,在颅骨层最弱,且各层感应电流密度值之比为32∶1∶190∶21,与电导率之比相近。结果表明,该模型可以很好地显示出人体头部各组织的电磁特性差异,为MIT系统研究提供可靠的依据。
颅脑模型;磁感应断层成像;有限元;电磁特性
引言
磁感应断层成像(magnetic induction tomography, MIT[1])技术通过求解逆问题进行图像重建,可以获得头部某一剖面的图像来反映脑组织的生理和病理变化。而MIT逆问题是通过多次迭代求解正问题去逼近的,因此正问题的算法对逆问题是十分重要的,如何快速、准确地求解出MIT正问题是MIT逆问题求解成功与否的关键。颅脑模型构造的研究是MIT正问题研究中的一个热点,也是正问题计算的基础。
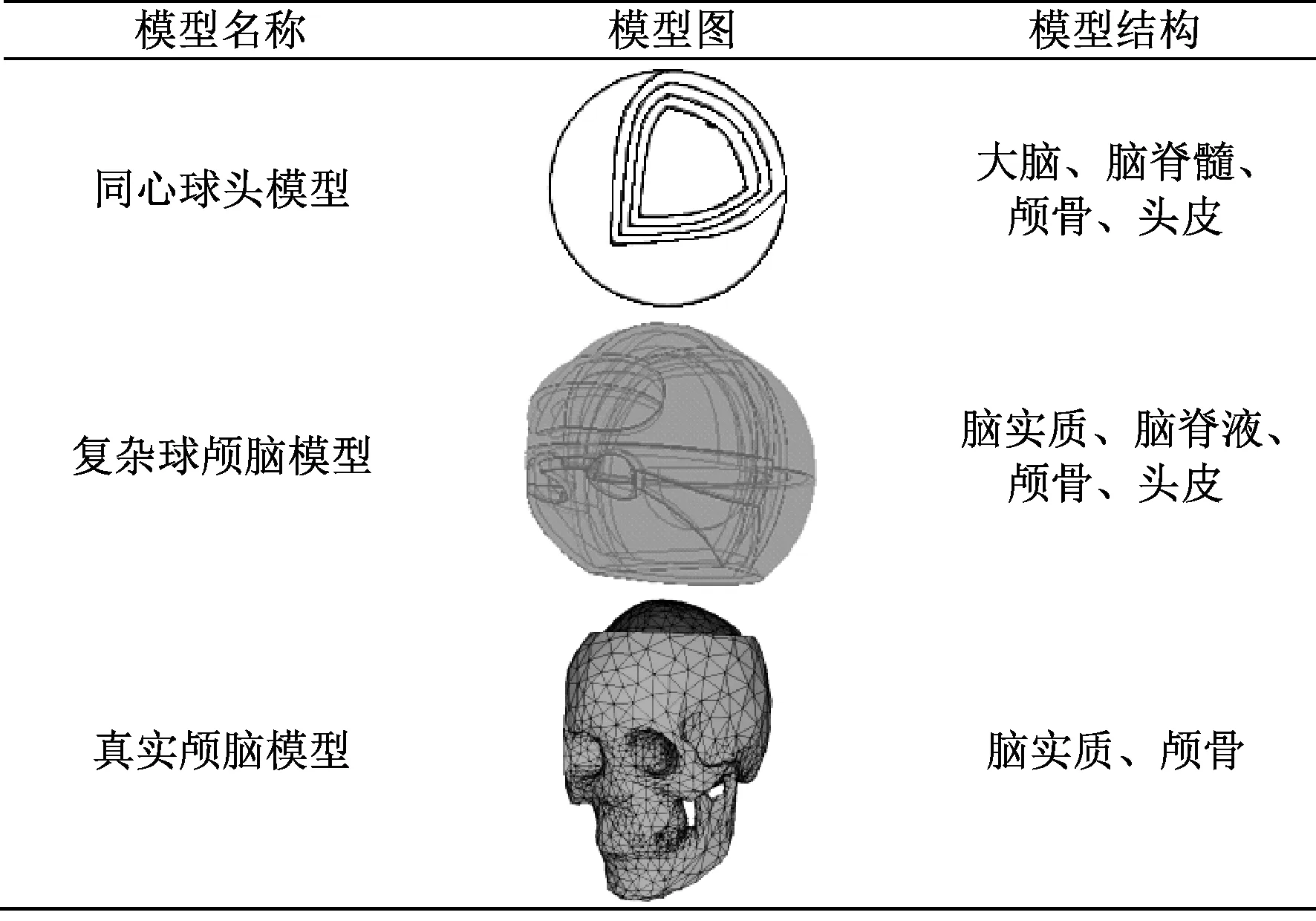
颅脑模型的构造主要涉及大脑各部分电磁特性和几何特性两方面,因此颅脑模型必须近似真实地反映颅脑各部分的电磁特性。同时,为降低计算的复杂度,模型构造应尽可能简单。在目前的研究中,出现的颅脑计算模型可以分为3类:球模型、复杂球模型和真实颅脑模型。研究人员早在1950年就开始用简单球模型[2]模拟人体头部,到1979出现了多层同心球模型[3]。球模型是对人体头部构造的一个简单近似,因此利用这样的模型对MIT正、逆问题进行求解必然会带来很大的误差。真实颅脑模型[4]是根据颅脑组织结构的真实情况而构建出的模型,其数据来源可以是解剖学的图像,也可以是通过医学成像设备(如CT、MRI和PET等)得到的医学图像,它在形状上更接近颅脑的真实构造,有利于计算精度的提高。但是,由于颅脑结构复杂,各组织电磁特性又不相同,使得利用真实颅脑模型的计算复杂度高。球模型精度差,而真实脑模型复杂度高,所以综合两种方法,一些学者提出了复杂球模型的构建理论,主要有重叠球模型[5]和Shepp-Logan模型[6]。复杂球模型构建相对简单,且具有与真实脑模型相当的精度,兼有真实脑模型和球模型共同的优点。
由于人体头皮、颅骨、脑脊液与人脑的电导率差距悬殊,因此本研究通过球、椭球等多个规则几何体的组合,以颅骨与脑实质的几何结构为主体,构建了一个逼近真实颅脑结构且具有头皮、颅骨、脑脊液、脑实质4层剖分结构的三维颅脑模型,为脑部电磁相关问题的计算提供便利。
1 颅脑模型的建立
目前,MIT系统常用的工作频率是10 MHz[7],且这个频率是医学应用的短波频率,对人体是安全的[8]。当激励频率为10 MHz时,线圈的趋肤深度约为线径的1%[9],电流几乎只在线圈的表面传输。因此,可以忽略线圈的线径,从而降低有限元网格的数量,提高计算效率。
在10 MHz下,人体头部主要组织的电导率特性如表1所示[4]。颅脑模型的主要剖分结构包含头皮、颅骨、脑脊液、脑灰质和脑白质等。由于人体头部的几何形状是由颅骨的组成和结构特点决定的,而皮肤是附着于颅骨上的一层组织,脑组织则填充于颅骨内,所以要确定颅脑模型的整体尺寸首先要确定颅骨的尺寸。而脑实质主要包括大脑和小脑,所以要建立接近真实颅脑结构的颅脑模型,首先要分析颅骨和脑实质的组成以及结构特点,构建颅骨模型和脑实质模型,才能完成具有近似真实颅脑结构的颅脑模型。而颅脑的几何轮廓整体呈卵圆形,结构较为复杂且不规则,无法用单一、规则的几何体来构建。因而本研究借助Comsol Multiphysics软件,通过以椭球为主的多个规则几何体的组合,以颅骨几何结构为主体,构建一个逼近真实大脑轮廓、具有4层剖分结构的三维仿真模型,为脑部电磁相关问题的计算提供依据。
表1 10 MHz下人体颅内主要组织的介电特性
Tab.1 The main tissue dielectric properties of human head at 10 MHz
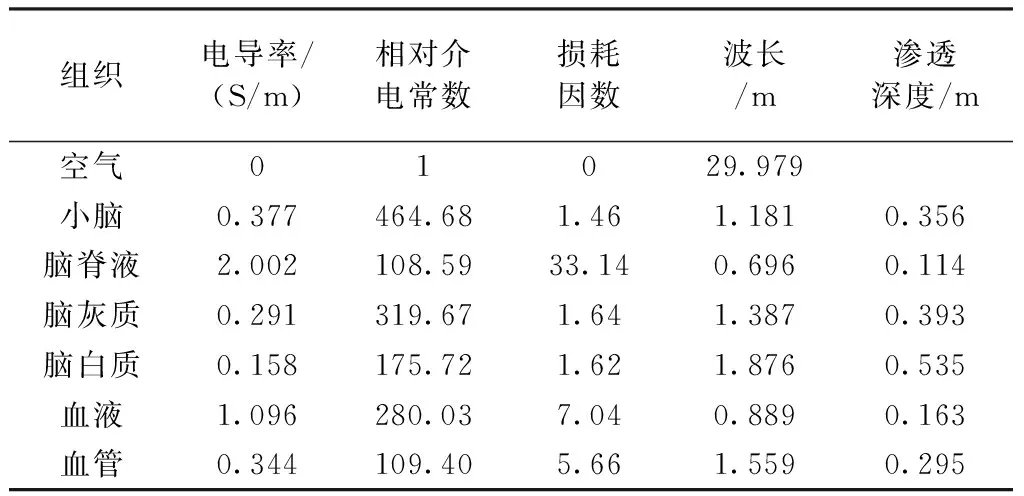
组织电导率/(S/m)相对介电常数损耗因数波长/m渗透深度/m空气01029.979小脑0.377464.681.461.1810.356脑脊液2.002108.5933.140.6960.114脑灰质0.291319.671.641.3870.393脑白质0.158175.721.621.8760.535血液1.096280.037.040.8890.163血管0.344109.405.661.5590.295
1.1 颅脑模型尺寸的确立
1)颅骨尺寸的确立:根据人体的解剖结构,眦耳线将人体的颅骨分为颅脑和颅面两部分(见图1),因为脑电特性的活动以及生理疾病所引起的功能变化是发生于颅脑内部,所以只需建立颅脑部分的仿真模型。参照普通成人颅骨的平均数据,其前后距约为19.0 cm,左右距约为17.0 cm,上下距约为17.0 cm,所以颅骨的前后距最大,左右距和上下距相近,确定总体结构以椭球体为主,椭球体的长轴对应颅骨的矢状轴[9]。
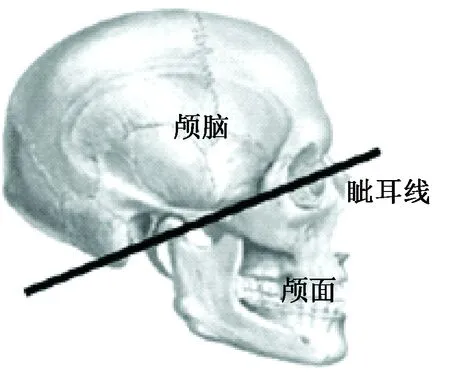
图1 人体颅骨结构Fig.1 Human skull structure
2)脑实质尺寸的确立:颅骨模型的前后、左右、上下按0.895∶0.882∶0.882的比例缩小后为颅骨内径。根据人脑结构(见图2)、大脑的体积(979~1 064 cm3)和颅骨内径,求出大脑前后距约为16.8 cm,左右距约为14.2 cm,上下距约为8.3 cm。

图2 人脑结构Fig.2 Brain structure
1.2 脑实质模型的构建
人脑的构造,主要包括脑干、小脑与前脑三部分(见图2)。脑干上承大脑半球,下连脊髓,呈不规则的柱状形。小脑位于大脑及枕叶的下方,恰在脑干的后面,是脑的第二大部分。小脑由左右两个半球所构成,且灰质在外部,白质在内部。前脑包括端脑和间脑,端脑包括左右大脑半球,是中枢神经系统的最高级部分,间脑由丘脑与下丘脑构成。本研究只建立前脑和小脑部分的仿真模型,具体的构建过程如下:
1)根据人脑结构特点,大脑的整体轮廓可以由不同大小的 2个椭圆近似构成,因此,在绘图界面分别插入2个实体椭球体,半轴长度X、Y、Z分别为(8, 7, 8.3)、(8.2, 7.1, 8.4),轴基准点分别为(0, 0, -0.5)、(0.6, 0, -0.5),取并集消除内部边界,用长方体截取,如图3所示。

图3 大脑模型Fig.3 Brain model
2)根据小脑的结构特点,将小脑简化为半椭球体,半轴长度X、Y、Z依次为(4.5, 5.8, 4),用长方体截取并将其置于小脑位置,模型如图4所示。

图4 脑实质模型Fig.4 Brain parenchyma model
1.3 颅骨模型的构建
具体的构建过程如下:
1)根据颅脑结构特点,模型整体轮廓可以由不同大小的3个椭圆体近似构成。因此,在绘图界面分别插入3个椭球体,椭球体的半轴长度X、Y、Z分别为(10, 9, 9)、(9, 7, 7)、(10, 8.5, 8.5),轴基准点分别为(0, 0, 0)、(0, 0, 2.5)、(0, 0, -1.8),取并集消除内部边界,如图5所示。
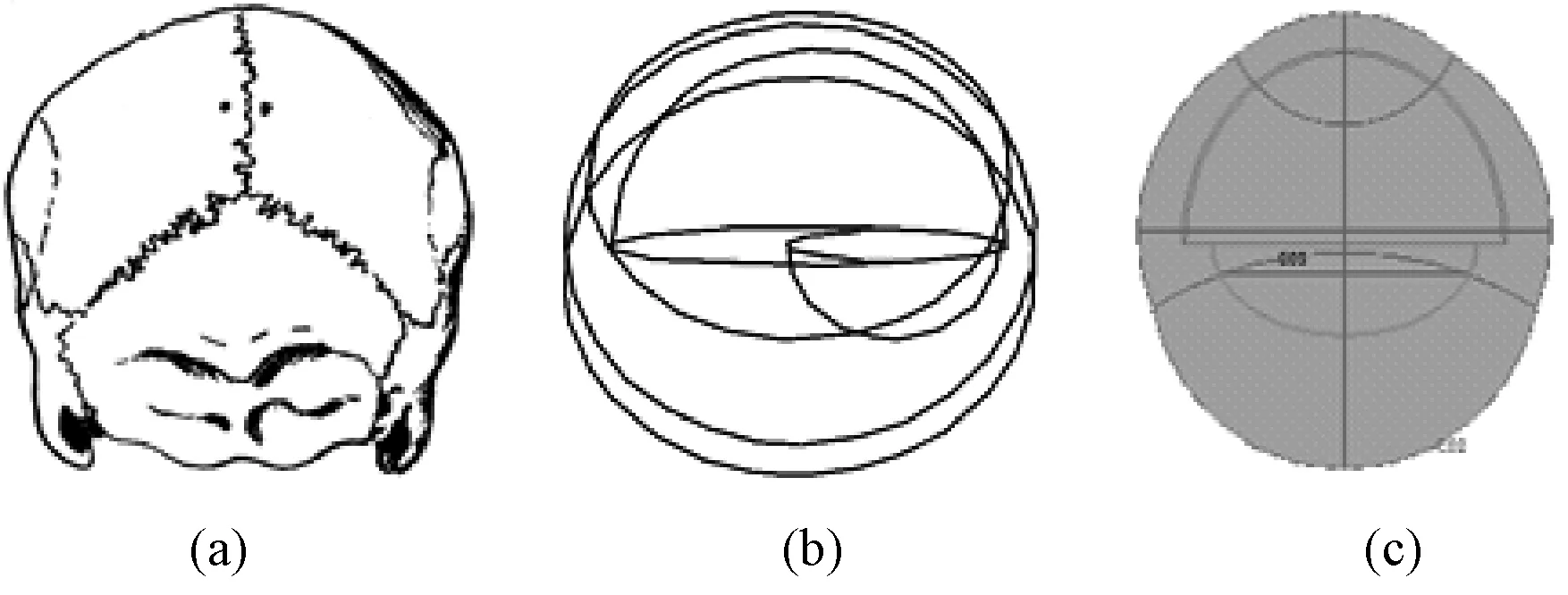
图5 颅骨模型整体轮廓构建。(a)真实颅骨后视图;(b)颅骨轮廓示意图;(c)颅骨轮廓图Fig.5 Construction of the overall outline of the skull model. (a) Rear view of the skull; (b) Contour sketch of the real skull; (c) Skull contour
2)枕骨较宽且弧度较小,因此对模型进行枕骨的修正。插入1个半轴长为(8, 9, 9)的椭球体,并将其置于枕骨位置,取并集消除内部边界,如图6所示。
3)对颅骨轮廓模型修正。绘制尺寸为(20, 20, 4)、轴向量为(1, 0, 1.73)的长方体,移动到眦耳线的位置,与模型取差集。用长方体对模型底部截取,使截取后模型的上下距为17.0 cm,得到颅骨轮廓模型,如图7所示。
4)颅骨额骨较窄且弧度较大,因此对模型进行额骨修正。插入1个半轴长为(3, 6, 4.2)的椭球体,并将其置于额骨位置,取并集消除内部边界,结果如图8所示。
5)对模型进行眼窝修正。在绘图界面放置2个半径为2.2 cm的球体,样式为实体。通过移动,将其放置在眼窝的位置并与原模型取差集,如图9所示,即为颅骨模型。

图6 枕骨轮廓修正。(a) 真实颅骨俯视图;(b)轮廓示意图;(c)枕骨修正图Fig.6 Correction of the occipital contour.(a)The real skull planform; (b) Contour sketch; (c) Correction of the occipital
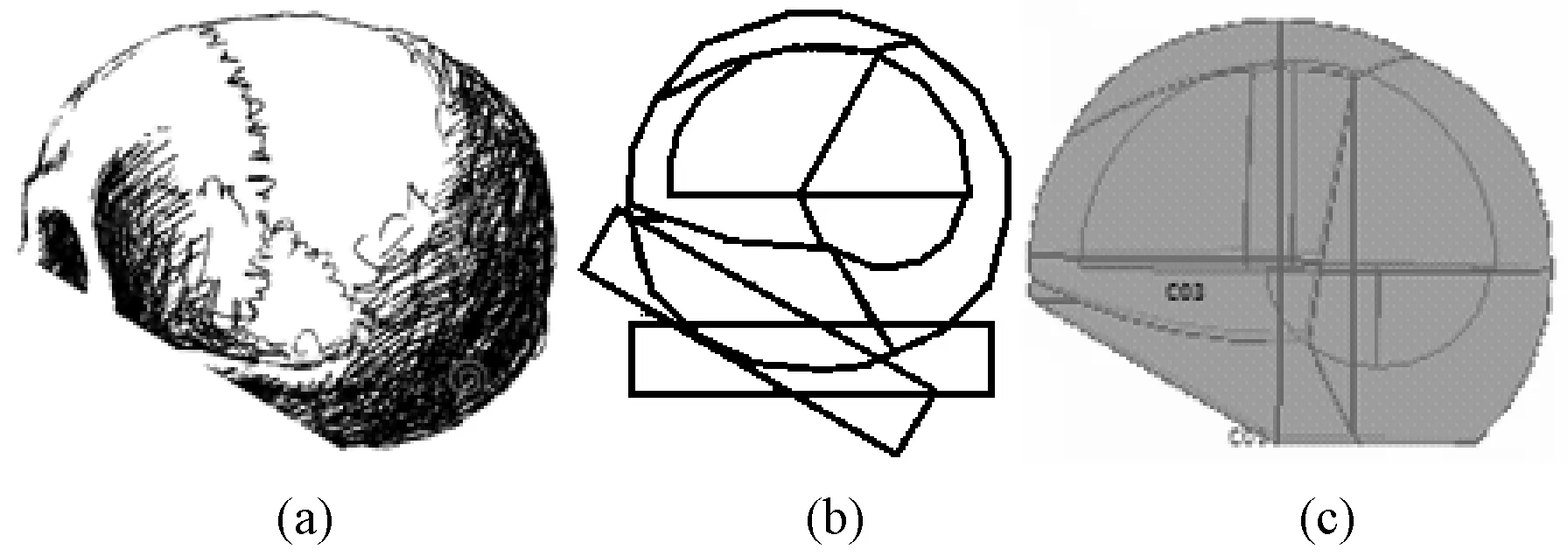
图7 颅骨轮廓修正。(a) 真实颅脑侧视图;(b)颅骨轮廓修正示意图;(c)颅骨轮廓修正图Fig.7 Correction of the skull contour. (a) Real cranial side view; (b) Correction skull contour;(c) Modified sketch of skull contour

图8 额骨修正Fig.8 Correction of the frontal
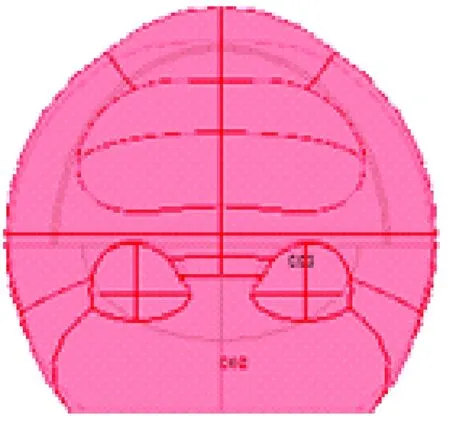
图9 眼眶修正Fig.9 Correction of the orbit
将额骨修正模型(见图8)复制,并按(0.895, 0.822, 0.822)的比例进行缩放,使缩小后的模型与颅骨轮廓模型间厚约1.0 cm,眼窝修正半径为2.3 cm,构成颅骨层。
1.4 头皮层与脊液层的构建
1.4.1 头皮
将额骨修正模型(见图8)复制,并按1.053∶1.059∶1.059的比例进行缩放,使放大后的模型比颅骨轮廓模型增厚约0.5 cm,眼窝修正半径为2.0 cm,构成头皮层。
头皮上有很多神经末梢,有些神经末梢距离大脑很近,头皮上的信息很容易传入大脑。头皮位于颅骨的外层,通常被分为皮层、皮下层、帽状腱膜层、腱膜下层、腱膜下间隙5个层次。其中,皮层是最厚的,并且内部布满了毛细血管,当头部受到外部损害时会产生流血现象;皮下层内部有大量的脂肪、纤维束和血管神经,是头皮结合至关重要的部位;帽状腱膜层位于颅脑上部,比较有韧性;腱膜下层和腱膜层下间隙都是结合形成头皮的重要部位。头皮厚度极薄,是除了眼皮以外人体最薄的皮肤;头皮又可分为真皮组织和表皮组织,其中真皮组织厚0.2 ~0.3 cm,表皮组织厚0.08~0.11 cm。考虑到电导率的影响,在研究中不可以忽略头皮层。
1.4.2 脑脊液
由于人体脑脊液与人脑的电导率差距悬殊,因此将脑脊液与脑实质区分开了,由颅骨与脑实质之间部分构成脑脊液层。
脑脊液是一种无色透明略有黏性的液体,充满于各脑室、蛛网膜下腔和脊髓中央管内。脑脊液由脑室中的脉络丛产生,又不断被吸收回流至静脉,不断地循环,循环途中任何部位发生阻塞均可引起脑积水。脑脊液在中枢神经系统起着淋巴液的作用,供应脑细胞一定的营养,运走脑组织的代谢产物,调节中枢神经系统的酸碱平衡。脑脊液保护脑和脊髓,维持颅内压,参与脑和脊髓的代谢,在脑和脊髓周围形成一个完整的液体垫,可以缓冲震动,分散压力,从而起到支持、保护和营养脑和脊髓的作用。脑脊液的性状和压力受多种因素的影响,若中枢神经系统发生病变、神经细胞的代谢紊乱,将使脑脊液的性状和成分发生改变;若脑脊液的循环路径受阻,颅内压力将增高。因此,当中枢神经系统受损时,脑脊液的检测成为重要的辅助诊断手段之一。
由皮肤层、颅骨层、脊液层、脑实质层,构成颅脑4层模型(见图10)。选择半径、高均为2 cm的圆柱面作为激励线圈仿真模型,线圈中心点位于xy平面,法线穿过线圈中心点与坐标原点。设置空气域为半径为20 cm的球体。

图10 4层颅脑模型Fig.10 Four layer brain model
2 仿真实验
2.1 颅脑模型的剖分
基于上述模型,进行相应的仿真实验,参数设置如下:求解域半径20 cm,6层剖分,模型4层,激励线圈中通入10 MHz、1 A的交流电。在边界设定中,空气域的边界面为磁绝缘,其他为连续。空气域的电参数与线圈域的电参数配置相同,相对磁导率为1,电导率为0,相对介电常数为1,自由网格参数较粗化,模型部分自由网格参数大小为0.005,单元增长率为1.5,其他为正常。对其进行四面体有限元网格剖分,图11为所得的颅脑模型系统有限元剖分图。
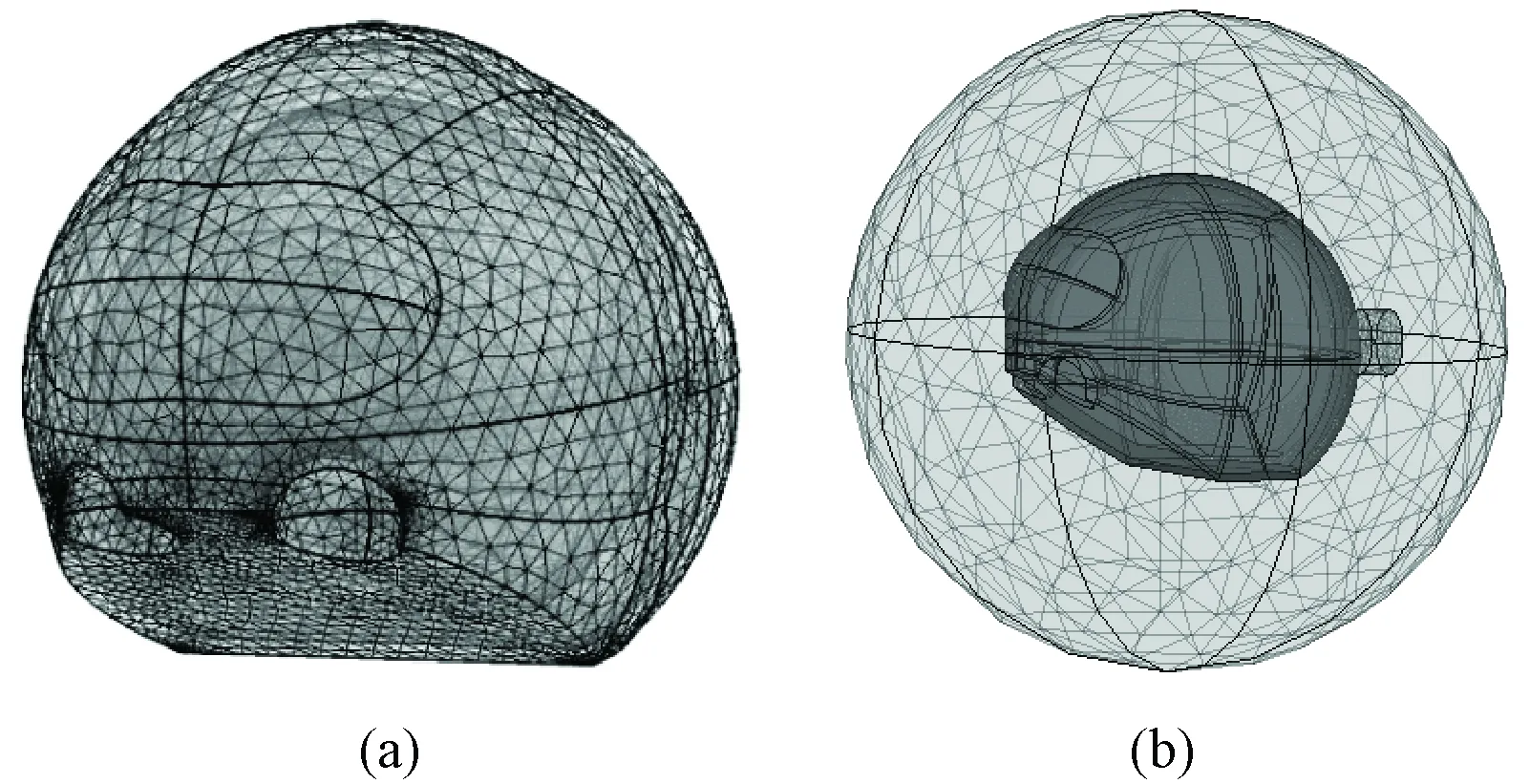
图11 颅脑模型系统有限元剖分图。(a)颅脑模型剖分图;(b)系统剖分图Fig.11 Finite element mesh of brain model system. (a) Mesh generation of brain model; (b) Mesh generation of MIT system
2.2 颅脑模型的求解
2010年,Dannhauerz等进行了人体的脑电源分析,并且给出了颅骨的电导率为0.01 S/m[10]。根据Bashar等的研究,头皮层的电导率为0.33 S/m[11]。因为皮质体积约占大脑半球体积的40%[12],由表1中脑灰质、脑白质的电导率与各自占大脑体积比例的乘积之和,得到脑实质电导率与相对介电常数值。颅脑模型各部分仿真参数如表2所示。
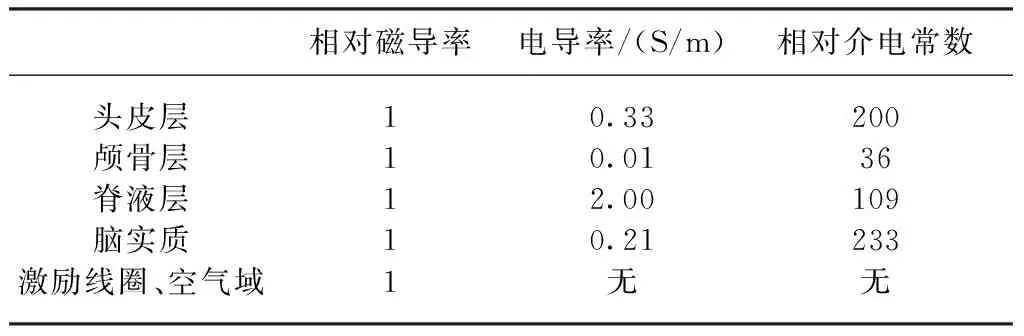
表2 颅脑模型各层仿真参数Tab.2 The brain model simulation parameters
接着对4层颅脑模型MIT仿真系统进行求解,求解器分析类型为时谐感应电流,采用稳态迭代GMRES线性求解器求解,预处理器采用几何多重网格法。通过后,处理得到颅脑模型的感应电流密度和磁场分布,结果如图12所示。
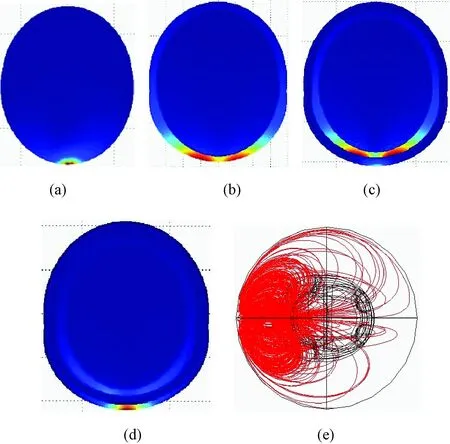
图12 颅脑模型感应电流和磁场分布。(a)单层模型感应电流分布;(b)2层模型感应电流分布;(c)3层模型感应电分布;(d)4层颅脑模型感应电流分布;(e)颅脑模型磁场分布Fig.12 Induced current and magnetic field distribution of brain model. (a) Induced current distribution of single layer model; (b) Double layer model; (c) Three layer model; (d) Four layer model; (e) Magnetic field distribution of brain model
在图12中,(a)为脑实质层感应电流强度分布,(b)为脑实质、脊液2层模型感应电流强度分布,(c)为脑实质、脊液和颅骨3层模型感应电流强度分布,(d)为4层颅脑模型感应电流强度分布;(e)为颅脑模型磁场分布,其中红线表示磁场的方向,流线通过激励线圈中心向空间发散,又回到线圈,形成回路。对图12中各图比较得出,头皮层、颅骨层、脊液层都能影响脑实质层的感应电流强度,其中脊液层的影响最大、颅骨层的影响最小。
3 结果
图12(a)~(d)可清晰地分辨出感应电流在模型各层结构的分布特点,即感应电流在皮肤层、脊液层较强,在颅骨层、脑实质层较弱。然而,图12为模型的粗略求解结果,不能作为感应电流在模型各层结构中敏感性分析的有效根据。为研究颅脑模型各层结构的敏感性,对颅脑模型做精细仿真。
图13为颅脑模型示意图。对颅脑模型分别做沿x轴从A到B和沿y轴从C到D的精细仿真,取从A到B和从C到D的感应电流密度分布,如图14所示。

图13 颅脑模型示意图Fig.13 Schematic diagram of the craniocerebral model

图14 颅脑模型感应电流密度值。(a) x轴上从A到B的值;(b) y轴上从C到D的值Fig.14 Induced current density of brain model. (a) The value from A to B on x axis; (b) The value from C to D on y axis
图14(a)的横坐标表示的检测范围为图13中沿x轴从A到B的检测点,且检测点关于中心点对称;纵坐标表示各检测点处对应的感应电流密度的模值。图14(b)的横坐标表示的检测范围为图13中沿y轴从C到D的检测点,纵坐标表示各检测点处对应的感应电流密度的模值。
4 讨论
4.1 颅脑成分对磁感应信号的影响分析
对比图13、14可以看出,颅脑模型与激励线圈关于y轴对称,图14(a)中的数据也关于中心点呈对称状态。图14(a)中感应电流密度的最大值出现在脊液层,最小值出现在颅骨层,头皮层与脑实质层的感应电流密度值相近。图14(b)中感应电流密度的模值受检测点到激励线圈距离的影响呈衰减状态,且衰减过程中各层与(a)中对应各层有相同的变化,即在颅骨层锐减,在脊液层突增,在脑实质层锐减。由于C处的头皮层距离激励线圈最近,感应电流密度出现最大值;而在D处的头皮层距离激励线圈最远,对应的感应电流密度值也最小。
对比图12、14可以看出,颅脑模型的感应电流密度在脊液层最强,对脑实质层的检测影响最大,因此不能忽略脊液层;感应电流密度在皮肤层较脑实质层强,对脑实质层的检测影响较大,不能忽略头皮层;感应电流密度在脑实质层较弱,而在颅骨层[13]的感应电流几乎为零,但颅骨层决定人体头部的几何形状,因此也不能忽略。各层中感应电流密度值有较大的起伏,这是因为感应电流强度分布与电导率分布有关。同时,感应电流强度在颅脑模型中的分布还与各检测点到激励线圈的距离有关。由表2数据可知,脊液层的电导率最大,所以产生的感应电流最大;头皮层的电导率相对较大,产生的感应电流也比较大;脑实质层的电导率相对较小,产生的感应电流就比较小;颅骨层的电导率几乎为零,产生的感应电流也就几乎为零。仿真结果表明,该模型可以很好地显示出人体头部各组织的电磁特性差异,可以作为MIT系统的颅脑计算模型。
由图14(a)分析得,头皮层、颅骨层、脊液层、脑实质层感应电流密度的均值约为1.60、0.05、9.50、1.05 A/m2,而对应各层的电导率分别为0.33、0.01、2.00、0.21 S/m。图14(a)为垂直于激励线圈法线的x轴上的感应电流密度分布,x轴上各点到激励线圈的距离差距较小。忽略距离的影响,各层感应电流密度值之比为32∶1∶190∶21,与电导率之比33∶1∶200∶21相近。由于图14(b)中数据受各检测点到激励线圈距离的影响较大,呈衰减状态,所以不能很好地显示感应电流值与对应各层电导率的关系。然而衰减过程中,感应电流值在各层中有与图14(a)中对应各层相同的变化趋势,从而说明颅脑模型各层中电导率差异对感应电流有与(a)中对应各层相同的影响。通过分析颅脑模型各层电导率差异与对应产生的磁感应信号的关系,进一步验证了该模型的可行性。
4.2 与其他模型的对比分析
常见的颅脑计算模型有球模型、复杂球模型和真实颅脑模型。将本研究中的4层复杂球颅脑模型与4层同心球头模型、2层真实颅脑模型进行对比,如表3所示。同心球模型的构建过于简单,与人体头部的构造有很大差异,利用这样的模型对MIT正、逆问题进行求解[14]必然会带来很大的误差。而赵璐璐等人构建的真实颅脑模型在形状上更接近颅脑的真实构造,但由于其构建过程和模型结构复杂,不利于后续的有限元剖分和求解计算,考虑到后续的网格剖分、计算机的内存容量和计算的时间等因素,只构建出包含颅骨层和脑实质两层结构的模型,而忽略头皮层与脊液层会对脑实质部分的检测产生很大影响。而在本研究中构建的4层复杂球颅脑模型,其构造接近于真实的颅脑结构,且构建过程比真实模型的构建过程简单,降低了有限元剖分和求解计算的复杂度;通过仿真计算,可以很好地显示出人体头部各组织的电磁特性差异,兼有真实脑模型和球模型共同的优点。
因此,本研究中的4层复杂球颅脑模型的构建过程相对简单,且与颅脑的真实结构近似,具有与真实颅脑模型相当的精度,仿真过程较真实颅脑模型简单,克服了球模型精度差、真实脑模型计算复杂度高的缺点。
表3 3种头模型的对比
Tab.3 The contrast of three kinds of head model
5 结论
颅脑模型的构造主要涉及大脑各部分电磁特性和几何特性两方面,因此必须近似真实地反映大脑各部分的电磁特性。同时,考虑到计算的复杂度,模型构造应尽可能简单。
本研究从人体颅脑的真实模型出发,通过Comsol Multiphysics有限元数值仿真软件的几何建模工具,用多个规则几何体的合并和分割,构建了一个近似真实颅脑结构的4层复杂球颅脑模型。仿真结果表明,该模型可以很好地显示出人体头部各组织的电磁特性差异,且模型构造接近真实颅脑结构,仿真过程也比真实的颅脑模型简单。结果表明,该复杂球模型兼有真实脑模型和球模型共同的优点,可以为MIT系统的设计提供参考。
[1] Yasin M. Imaging of hemorrhagic stroke in magnetic induction tomography: an in vitro study [J]. International Journal of Imaging Systems and Technology, 2014, 24(2): 161-166.
[2] Wilson FN, Bayley RH. The electric field of an eccentric dipole in a homogeneous spherical conducting medium [J]. Circulation, 1950, 1(1): 84-92.
[3] Cuffin BN, Cohen D. Comparison of the magnetoencephalogram and electroencephalogram [J]. Electroencephalography and Clinical Neurophysiology, 1979, 47(2): 132-146.
[4] 柯丽,赵璐璐,杜强. 颅脑血肿MIT涡流场仿真与分析[J].系统仿真学报,2014,26(3):517-522.
[5] Huang MX, Mosher JC, Leahy RM. A sensor-weighted overlapping-sphere head model and exhaustive head model comparison for MEG [J]. Physics in Medicine and Biology, 1999, 44(2): 423-440.
[6] 孙丰荣, 刘泽, 李艳玲, 等. 基于模型的CT三维医学图像重建仿真 [J]. 系统仿真学报, 2006, 18(3): 781-784.
[7] 李烨, 董秀珍, 刘锐岗, 等. 磁感应断层成像中的一种高精度同步相位测量方法 [J]. 仪器仪表学报, 2009, 30(4): 796-801.
[8] 秦明新. 检测脑水肿的磁感应成像测量方法研究 [D]. 西安: 西安电子科技大学, 2005.
[9] 王雷. 脑磁感应断层成像正问题的三维有限元仿真研究 [D]. 西安: 第四军医大学, 2013.
[10] Dannhauer M, Lanfer B, Wolters CH, et al. Modeling of the human skull in EEG source analysis [J]. Human Brain Mapping, 2010, 32(9): 1383-1399.
[11] Bashar MR, Li Y, Wen P. Effects of local tissue conductivity on spherical and realistic head models [J]. Australasian Physical & Engineering Sciences in Medicine, 2010, 33(3): 233-242.
[12] Henery CC, Mayhew TM. The cerebrum and cerebellum of the fixed human brain: efficient and unbiased estimates of volumes and cortical surface areas [J]. Journal of Anatomy, 1989, 167: 167-180.
[13] 柯丽,李盼盼,陈红.颅骨对磁感应断层成像信号检测影响的仿真与实验研究[J].中国生物医学工程学报,2015,34(5):566-573.
[14] 柯丽,曹冯秋,杜强.MIT中反投影矩阵的计算与数据处理方法[J].仪器仪表学报,2014,35(10):2256-2262.
Establishment of a Four Layer Complicated Ellipsoid Brain Model
Ke Li1Gao Yanzhao1Du Qiang1Han Ling2
1(SchoolofElectricalEngineering,ShenyangUniversityofTechnology,Shenyang110870,China)2(SchoolofSino-DutchBiomedical&InformationEngineering,NortheasternUniversity,Shenyang110819,China)
The study of brain model establishment is the basis of intracranial imaging, and it is also the necessary condition for the calculation of forward problem solution in the magnetic induction tomography (MIT) system. According to the brain structure, a four layers complicated ellipsoid brain model was established through a finite element simulation software Comsol Multiphysics. Firstly, the brain parenchyma model was constructed according to the brain volume and the skull inner diameter. Secondly, the skull model was constructed according to the human anatomy structureand the contour, occipital, frontal and orbit of the model were corrected. Thirdly, the head cortex, skull and spinal fluid layer were constituted by scale model of the skull, and the four layers brain model were constituted together with the brain parenchyma layer. Finally, put the model into alternating current magnetic field of 10 MHz, and gave the induced current distribution of scalp layer, skull layer, spinal fluid layer and parenchymal layer. The induced current was strongest in the spinal fluid layer and weaker in the skin layer and the parenchymal layer, while was the weakest in the skull layer. The ratio of the induced current density values in each layer was 32:1:190:21, closed to the ratio of electrical conductivity. The simulation experimental results showed that the model could display the difference of the electromagnetic characteristics of human head tissues, providing reliable data for MIT system.
brain model; magnetic induction tomography; finite element; electromagnetic characteristics
10.3969/j.issn.0258-8021. 2016. 01.007
2015-06-01, 录用日期:2015-11-29
国家自然科学基金(51377109);辽宁省自然科学基金(2013020050);辽宁省教育厅重点实验室基础研究项目(LZ2014011)
R318
A
0258-8021(2016) 01-0055-08
*通信作者(Corresponding author), E-mail:ke.l@live.cn
