例谈“整理与复习课”的教学策略

□蔡雯丽

例谈“整理与复习课”的教学策略

□蔡雯丽

通过整理与复习课的教学，有利于巩固学生在小学阶段所学的基础知识和基本技能，对知识形成过程有全面、结构化的认识，提升灵活运用所学知识解决实际问题的能力。结合“立体图形的整理与复习”的教学实践，提出教师应该从“挖掘联系，串联计算方法；对比理解，活用解决问题；优化结构，完善复习方法模型”三方面来对六年级总复习课进行教学实施。

立体图形 整理与复习

人教版六年级下册第六单元的教学内容是“整理和复习”。通过整理和复习课的教学，可以有效巩固学生小学阶段所学的基础知识和基本技能，对知识形成过程有全面的、结构化的认识，渗透数学思想方法，发展思维，提升灵活运用所学知识解决实际问题的能力。那么六年级的整理与复习课该怎么上？笔者以“立体图形的整理与复习”教学为例，就此问题进行了重新认识与思考。

一、教材分析

“立体图形的整理与复习”属于“图形与几何”领域的整理与复习，教材将这一领域的复习分为“图形的认识与测量”“图形的运动”以及“图形与位置”三条主线展开，这一课时属于图形的认识与测量，教材上安排了如下两个例题。

例4是整理和复习立体图形的特征。例5是整理和复习四种立体图形的表面积、体积的计算公式。

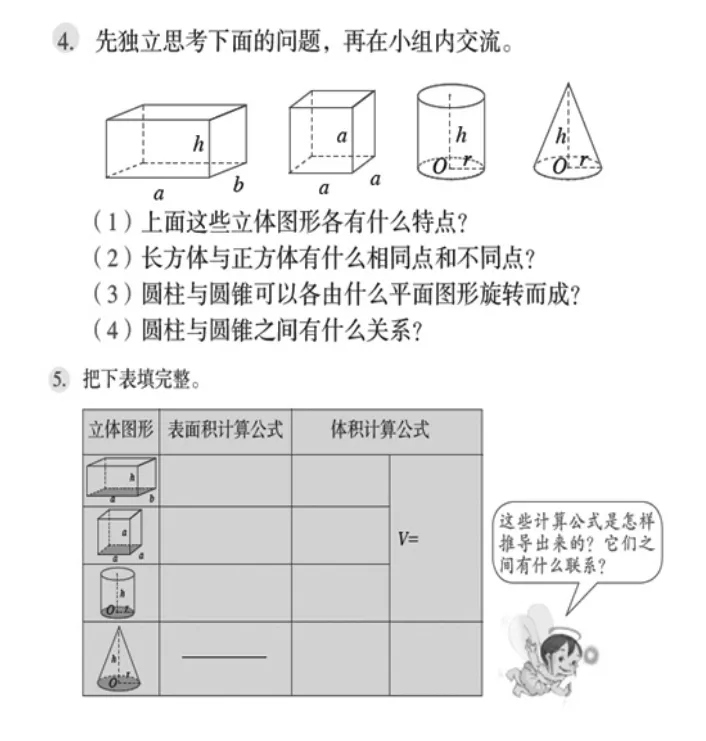
例4将小学阶段学过的立体图形集中在一起，并通过提问的形式复习它们的特征及各组成部分的名称，比较相同点和不同点，沟通立体图形与平面图形之间的联系。例5通过填写表格的方式掌握计算公式，并且通过小精灵的话厘清计算公式的推导过程，从而沟通长方体、正方体与圆柱体积之间、圆柱与圆锥体积之间的联系，形成知识网络。例题后的练习中基本上可以分为求非规则物体的体积计算、立体图形的三视图以及表面积、体积的基本计算及在生活中的应用四个方面。

本节内容是小学阶段“图形与几何”知识领域有关立体图形的系统整理与复习，覆盖的内容很广，不可能面面俱到，也不可能仅靠这一节课上完。那么这节复习课，我们应该找准哪些复习的“点”？笔者认为，要找准复习的“点”，必须要聚焦三个核心点：一是建立表面积和体积概念内涵，会进行相应的计算是基础；二是作为一节整理与复习课，沟通几何图形知识之间的关系（平面与立体、立体与立体），优化认知结构，形成知识网络是手段；三是从能力提升而言，帮助学生形成几何形体的表象，建立空间观念，融会贯通，提高解决问题的能力是目的。

二、教学策略

【片段1】挖掘联系，将计算方法“串”起来

作为一节立体图形整理与复习课，对表面积和体积概念内涵进行理解，会熟练进行相应的计算是本节课的目标之一。但是由于不同的立体图形分布在各个年级中学习，学生往往只是对一个个公式进行单纯的记忆，却对它们内在的联系、公式的来龙去脉缺乏一定的认识。因此通过将图形归类来认识立体图形内在的联系；通过想象侧面展开图，沟通平面与立体之间的关系，既是将一个个计算公式串起来，又加深了对表面积和体积概念内涵的理解。

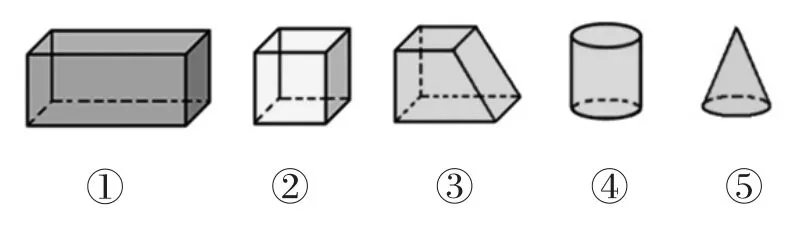
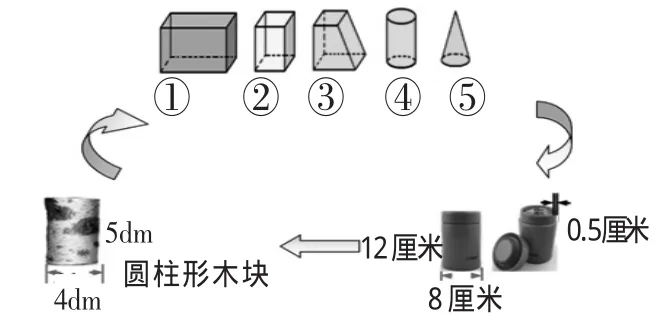
1.出示图形。

提问：这5个立体图形，哪些可以归为一类？

出示要求：分一分：哪些归为一类？说一说：为什么把它们归为一类？

2.交流反馈。

生：①②③为一类，因为这3个没有曲面，而后面2个有曲面。

师：他是从图形的特征来归类的，前3个图形都有6个面，还有8个顶点、12条棱。这种分类是正确的。

生：①②④一类，因为它们都是直柱体。

生：我也是按是不是直柱体来分的，但我觉得①②③④是一类。

师：③号图形到底是不是直柱体？说明自己的理由。

生：我觉得不是，因为它上下两个面不一样大。

生：我觉得是，虽然它上下两个面不一样大，但是它前后两个面一样大！

生：我觉得是，只要把这个图形转一转，上下两个面就都是梯形了，可以看成是梯形平移得到的。

师（引导）：按你们的意思来说，要判断一个图形是不是直柱体的标准是什么？

生：上下一样粗细，而且上下两个面一样大。

师（明确）：也就是说，可以由一个面平移得到另一个面，是这样吗？（生点头）

师：按照这样的标准，我们来看看③号图形到底是不是直柱体？（学生发现：原来它是前面的面向后平移得到的，也是直柱体）

师：想象一下，其他几个立体图形是怎样平移得到的？用手势表示一下。

小结：原来①②③④都可以通过底面的平面图形平移得到，所以它们都是直柱体。

师：那你们知道直柱体的体积怎样计算吗？

生：直柱体体积都可以用底面积×高来表示。

师：这又是为什么呢？

生：高就是底面平移的距离，所以直柱体体积就是底面积×高。

师：除了体积有一样的公式，它们的侧面积呢？

生：直柱体侧面积=底面周长×高，因为侧面都是长方形。

师：拿着手上的长方形纸折一折几个立体图形的侧面给同桌看一看。

（重点反馈③号图形，教师用教具模型演示）

3.沟通小结。

师：刚才同学们从运动平移的角度发现了立体图形之间的联系，从运动的角度看，这些图形还有没有不同？

生：⑤号圆锥可以通过旋转得到。

生：④号圆柱除了可以通过圆形平移得到，还可以通过长方形绕长或宽旋转得到。

师（引导）：通过刚才的交流，你有什么感受？

生：图形间是有关系的。

生：不同的平面图形经过运动变换得到了不同的立体图形。

【思考分析】

教材中立体图形的相关知识是分散编排、螺旋上升的，要把相对独立的立体图形整体把握，就要加深对知识的理解与沟通，寻求知识内部的联系，提升对图形的认识。这一片段中，转化这一思想方法，就是变“点”为“线”的关键。

1.动态转化，发展空间想象。

“这5个立体图形，哪些可以归为一类？”这一主打问题引导学生从整体的角度来重新认识这些立体图形。有的从图形基本的面、顶点、棱的特征来加以分类；有的则从运动转化的角度加以分类。通过二维到三维的运动转化，发现立体图形和平面图形间存在着密切的联系：立体图形可以通过平面图形旋转或者平移得到。学生在比画想象运动轨迹的过程中发展着空间想象能力。

“③号图形也是直柱体吗？”引导学生聚焦这个教材中不曾学到过的图形，学生在以往的学习中已经有了类比、合情推理的能力，在六年级整理与复习这一对知识总结与综合运用的阶段，将新的图形与已学过的图形进行类比沟通，用合情推理、从动态运动转化的角度沟通直柱体之间的联系，完善认知结构。

在分类的过程中将各种信息聚集起来进行分析整合，通过寻找图形的共同点，发展学生的求同思维。

2.有序转化，理解方法本源。

“为什么直柱体的体积可以用底面积×高来表示？”这一问题引领学生将零散的各个立体图形的体积公式变成“底面积×高”这个通用公式。因为都是可以由底面平移一定的高度得到，将静态图形变为动态发展，从运动观点沟通图形体积计算的联系，构建成网络，渗透数学思想方法，让知识由厚变薄。

“为什么侧面积都可以用底面周长×高来解决？”因为它们的侧面积展开图都是长方形，求侧面积的本质就是求长方形的面积，而长方形的长就是立体图形底面的周长，宽就是立体图形的高。

几个立体图形长得虽然不一样，但是通过分析概括抽象，发现它们有着共同的本质，发展了学生的逻辑思维。

【片段2】对比理解，让解决问题“活”起来

在平时的练习中，学生对于直接计算的问题基本上不会出错，但当条件比较隐蔽、需要转化时，错误率往往会提升。主要是学生对基本的直接问题与发展后的间接问题不能很好地加以联系，因此要将知识置于多变的问题情境之中，通过对比理解，让解决问题“活”起来。

师：这些立体图形都可以代表我们生活中各种各样的物体，比如说圆柱，你想到了关于保温杯的哪些问题？

生：这个保温杯可以装多少水？生：需要多大的盒子才能装得下这个保温杯？生：用包装纸包保温杯盒子，需要多大的包装纸？根据学生的回答生成以下问题，请学生解答：（1）给这个保温杯做个无盖保护套，需要多大的布料？（2）这个保温杯能容纳多少毫升水？（3）至少需要多大的纸盒才能装下保温杯？

对比1：这个问题实际上就是要解决——（区分表面积和体积）

对比2：得数要求保留整数，分别是多少？（进一法、去尾法、四舍五入法）

【思考分析】

面对需要复习的多种知识点，我们要有取舍整合：根据课后配套的习题；根据本节课复习的核心——规则物体表面积和体积，抓准基础知识；根据平时这一模块中学生的易错点和混淆点。在这三个“根据”的驱动下，编制题组同时呈现，根据学生的解答进行分析。

保温杯能容纳多少毫升水？

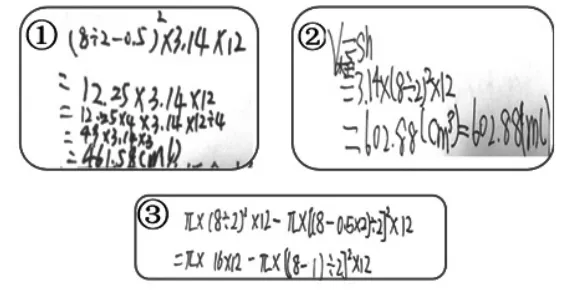
给保温杯做个无盖保护套，需要多大的布料？

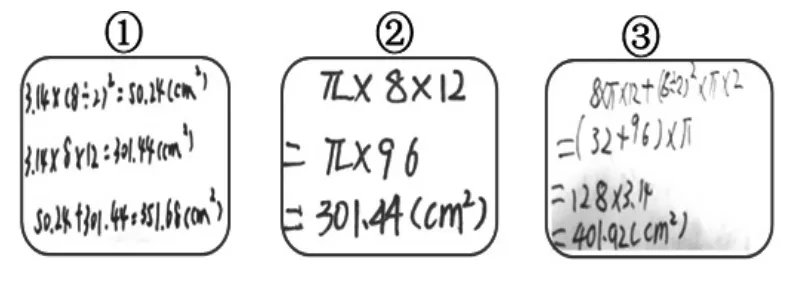
在分析中进行第一次对比“都是解决保温杯问题，有什么不同”，从而明确在解决具体问题时首先要分析情境和什么有关，是求表面积呢，还是求体积？如果是求表面积，还得特别注意有几个面。呈现三个问题的正确答案后进行第二次对比“得数要求保留整数，分别是多少？”明确我们需要根据实际情况对结果进行合理的处理。两次对比，在练习中关注知识点之间的联系，让学生在观察、尝试、运用、比较的过程中建立情境之间的联系，加深对知识的再认识、理解和运用。

【片段3】优化结构，完善复习方法模型

通过整理与复习，将零散的知识点通过各种途径沟通联系串起来，我们试图让知识由厚变薄，从单独的变成一个整体；同时，我们也要注意知识的拓展应用，完善方法模型，优化方法结构，让方法由薄变厚，让一种方法拓展到一类课型。

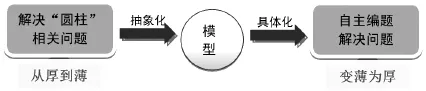
师：回忆一下，今天我们是怎么来复习立体图形的？

自主编题应用：

想一想：比画一下，这些物体有多大？可能是什么？

编一编：选择其中一个物体，编一编生活中的相关问题。

用一用：用你今天所复习的知识解决同桌的问题。

【思考分析】

弗赖登塔尔认为，数学化有横向数学化和纵向数学化之分，横向数学化“是把生活世界引向符号世界”，而“在符号世界里，符号的生成、重塑和被使用”，则是纵向数学化。

在横向数学化的过程中，我们通过运动感受立体图形和平面图形之间的关系，将一个个公式通过直柱体沟通联系，梳理立体图形本身之间的关系；通过重点解决圆柱的相关知识，将表面积、体积的实际应用以及“进一法”“去尾法”“四舍五入法”等处理结果的方法放置于一个情境中，抽象出复习的模型，让学生经历了知识从厚到薄的过程。

在纵向数学化的过程中，学生利用圆柱的复习方法，自主编题解决其他立体图形。这是一个触类旁通的过程，也是从圆柱复习模型具体化到更多立体图形的过程，让学生经历了方法从薄到厚的过程。发现原来很多问题都是以这样的原始模型出现的，它们原来是一类的，我们基本上都可以用这样的方式去解决，优化结构，构建方法模型。

[1]陈庆宪.理顺解题思路 拓展空间想象——“立体图形体积计算”复习教学实录与思考[J].小学教学（数学版），2013（5）.

[2]魏光明.让认知结构具有生长活力——试谈数学复习课的改革路向[J].人民教育，2008.

（浙江省杭州市学军小学 310012）