挖掘教材内涵 渗透基本思想——以“极限思想”的教材研读及教学实施为例

□郑维荣

挖掘教材内涵 渗透基本思想
——以“极限思想”的教材研读及教学实施为例

□郑维荣

数学基本思想是蕴含于数学知识技能教学中的“隐性”内容。对于教师而言，唯有读懂教材内容背后隐含的数学基本思想，方能在组织教学时有的放矢、有效施教。以极限思想为例，教师在教学中如果能够把握极限思想的出发点、增长点及突破点，就能较好地达成教学目标。

教材研读 基本思想 极限思想

曾有教育家说过：当学生把学过的所有知识都忘记，剩下的便是教育。笔者以为，就数学教育而言，当学生把学过的所有数学知识都忘记，剩下的便是数学的基本思想及活动经验。史宁中教授认为：“数学思想需要满足两个条件：一是数学产生过程中所必须依赖的那些思想，二是学习过数学的人所具有的思维特征。”如转化思想、符号化思想、分类思想、集合思想等，都属于学生通过数学学习应该了解、掌握的数学基本思想。然而，相对于知识技能这样跃然纸上的教学“明线”而言，基本思想这条“暗线”确实让一线教师困于琢磨、难以把握。为此，笔者查阅了大量的文献资料，经过阅读与反思，发现通过研读教材、挖掘内涵、相机渗透是基本思想教学的必由之路。下面笔者以“极限思想”为例展开阐述。

极限思想相对于其他基本思想更为抽象。因此，在小学阶段，“极限思想”的学习离不开“无限思想”的积累，主要是让学生通过相关数学知识的学习，适度体会“无限”，进而感受“极限”。为此，人教版在各册小学数学教材中都安排了相关内容，来丰富学生的相关认知。以下仅作简要列举（见下表）。

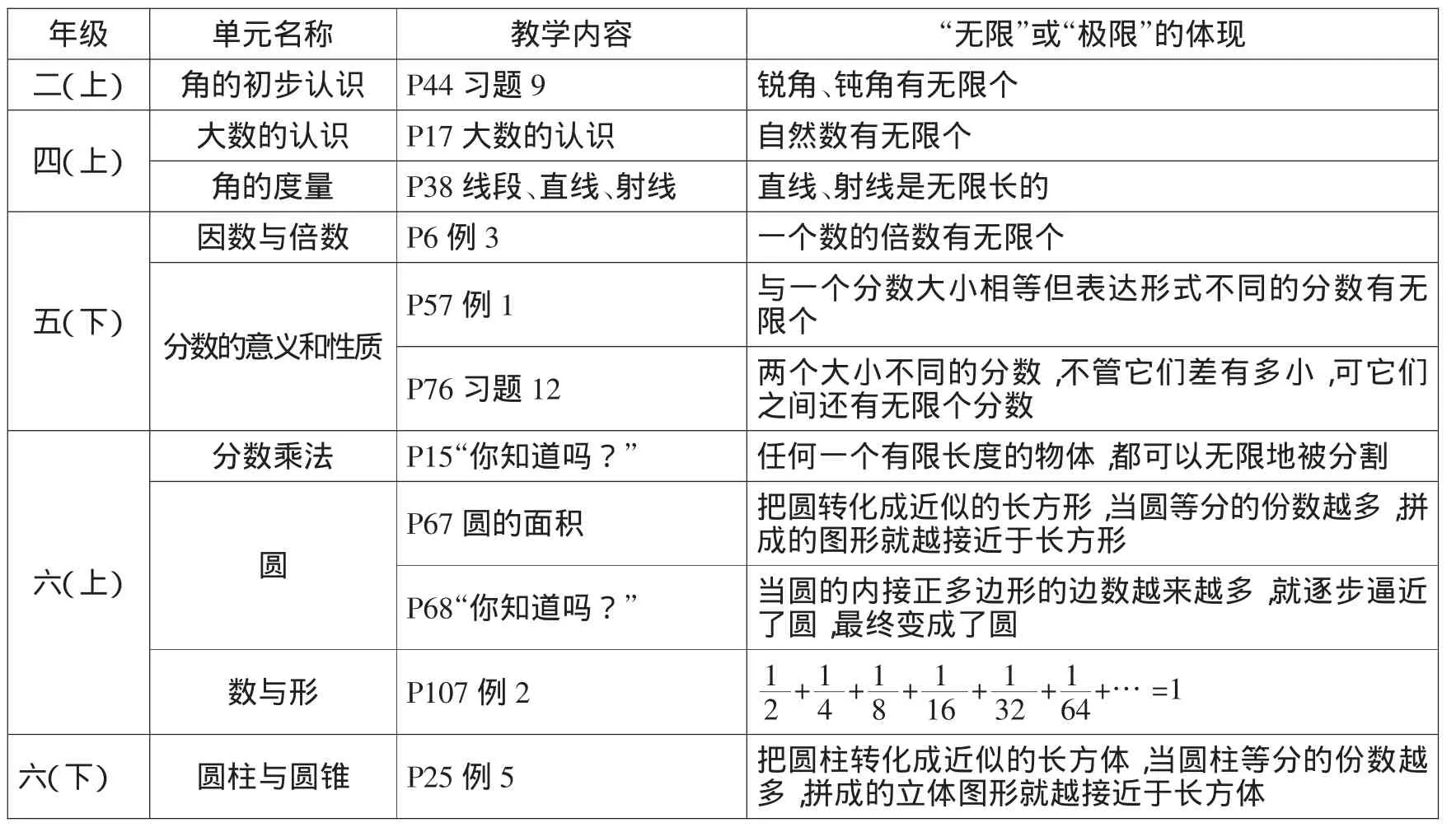
年级 单元名称 教学内容 “无限”或“极限”的体现二（上） 角的初步认识 P44习题9 锐角、钝角有无限个四（上） 大数的认识 P17大数的认识 自然数有无限个角的度量 P38线段、直线、射线 直线、射线是无限长的因数与倍数 P6例3 一个数的倍数有无限个五（下）分数的意义和性质P57例1 与一个分数大小相等但表达形式不同的分数有无限个P76习题12 两个大小不同的分数，不管它们差有多小，可它们之间还有无限个分数分数乘法 P15“你知道吗？” 任何一个有限长度的物体，都可以无限地被分割六（上）4＋…=1六（下） 圆柱与圆锥 P25例5 把圆柱转化成近似的长方体，当圆柱等分的份数越多，拼成的立体图形就越接近于长方体P67圆的面积 把圆转化成近似的长方形，当圆等分的份数越多，拼成的图形就越接近于长方形P68“你知道吗？” 当圆的内接正多边形的边数越来越多，就逐步逼近了圆，最终变成了圆数与形 P107例2 1圆2＋14＋18＋116＋132＋16

读懂教材内容隐含的基本思想，是达成教学目标的基本前提。下面，笔者围绕三个方面，谈谈教材研读及教学实施的一些建议。

一、把握极限思想的“生发点”

通过上表对各册教材中极限思想渗透点的分析，我们不难发现，编者对于极限思想的教学安排是由易至难、逐步深入的。这样的教学安排非常适合正处于抽象意识、概括能力形成过程中的小学生的认知规律。学生通过数数，发现“自然数的个数是无限的”；通过想象，发现“直线、射线是可以无限延长的”；通过运用相关的数学知识，知道“一个分数可以写出无限个与它大小相等但形式不同的分数”……虽然这里存在“无限”现象，但对学生而言，立足原有的知识经验，借助具体的学习情境，还是能够理解并形成无限思想的。

正是由于学生积累了这么多的无限思想，极限思想才有可能渗透到学生的数学思维中。因此，教学过程中，我们应牢牢把握这些极限思想的生发点，帮助学生更好地从“无限”过渡到“极限”。比如，六年级上册教材中的“圆的面积”（如图1），便是典型课例。它是学生思维从“无限”走向“极限”的重要环节，是其感悟极限思想的不可或缺的生长点。学生通过动手操作，借助数形结合的方法，直观感知了“把圆平均分的份数越多，每一份就越小，拼成的图形就会越接近于一个长方形”。教学中还可借助“几何画板”等软件，让学生观察“份数多到极致”的画面，得出“此时就能拼成长方形”的结论，进而推导出圆面积计算公式，从中体会极限思想，并为后续相关学习积累经验。

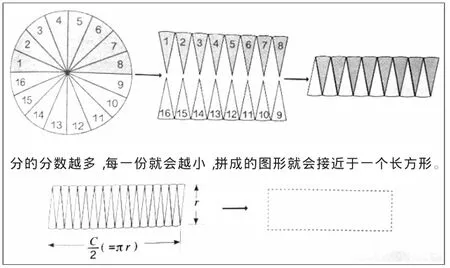
图1

二、领会极限思想的“增长点”

如果说，学生通过圆面积计算公式的推导过程初步感受了极限思想，那么，六年级上册教材“数与形”中例2的学习（如图2），则是学生深入触碰极限思想的一次经历。教材以“计算＋…”为例，让学生通过计算、观察、想象、归纳与总结，得出“和为1”的结论。

图2

通过对教材的分析，我们可以发现，编者依旧采用了循序渐进的编写方式，拉伸学生自主体验的过程：呈现数学问题——化难为易，在简单计算中寻求规律——借助数形结合，感受“随着加数个数不断增多，计算结果所表示的图形面积（线段长度）越来越接近于1，最终等于1”——得出“和为1”的结论。

教学实践表明，学生从“结果无限接近于1”过渡到“结果就是1”的思维转变是“艰难”的，甚至部分学生认为“这是绝对不可能的”。确实，学生出现这样的学习“危机”也是情理中的事。但换个角度来看，这个思维转变的过程，其实就是从“无限思想”到“极限思想”的增长过程。为帮助学生顺利实现这种“思想增长”，教材巧妙借助数形结合的直观优势。不光适时出示了“圆形图”，还跟进呈现了“线段图”。这样的“两条腿走路”的双重解释，正是编者考虑到学生“思想增长”的难度而做出的安排。教学过程中，我们应领会教材意图，于学生困惑处、愤悱时，细化组织，优化点拨。笔者在执教本课时，在对教材的两幅图进行了动态展示的基础上，还增加了“圆面积计算公式推导”的过程演示，为学生实现数学思想的深层跨越提供了新的抓手。

三、捕捉极限思想的“突破点”

学生对极限思想的学习，之所以困难重重，这是因为它高度的抽象性所决定的。因此，作为教师，不仅要在课前潜心研读教材，挖掘文本内涵，而且还要在教学现场及时捕捉有利于渗透极限思想的突破点，让学生在有限的学习时间中尽可能充分地感悟、形成极限思想。

例如，前文提到的“数与形”教学中，在学生利用“线段图”解释“计算结果等于1”的过程中，笔者根据学生的回答，随机安排了一次现场操作活动：让学生动手剪取一根绳子（即单位“1”）的，，…，切身感受“取得越多，剩下的便越少；直至没法再取，便可理解成取了全部”。就这样，在数学思想的教学中，让学生适时地“慢下来”，停一停，动一动，想一想，悟一悟，无疑比“就题说题”更有意义。

另外，教师及时、恰当的归纳总结，也是促进学生将极限思想纳入自身认知体系的有效策略。当学生学完全课后，教师可以这样总结：“今天的学习中，我们一直在与‘无穷无尽’打交道，它需要我们一直往下想、往下分，永不停止。然后，猜想出最后的结果。这里面，就蕴含着一种非常重要的数学思想，叫作极限思想。”

正如史宁中教授所说的：“数学思想是一种智慧，不是教出来的，而是悟出来的。”作为教师，我们应竭力厘清教材内容背后隐含的数学思想，并通过自己的合理组织，为学生感知思想、体会思想、认同思想、建构思想提供强力支撑。

[1]史宁中.数学的基本思想[J].数学通报，2011（50）.

[2]王永春.再论极限思想[J].小学教学（数学版），2015（5）.

（浙江省绍兴市上虞区丰惠镇中心小学 312300）