插值多项式的构造与类范德蒙行列式的计算

孙玉香， 许 勇

(安徽师范大学 数学计算机科学学院，安徽 芜湖 241003)

插值多项式的构造与类范德蒙行列式的计算

孙玉香， 许 勇

(安徽师范大学 数学计算机科学学院，安徽 芜湖 241003)

利用Newton插值多项式及差商的计算给出了类范德蒙行列式的计算公式的显示表达式；且在实际计算中很容易在计算机上实现.

插值多项式;差商;类范德蒙行列式

1 预备知识

1.1 插值多项式

插值多项式的应用非常广泛如股票分析、计算机图形学、计算生物学、医药卫生、天文等，但它构造的基本方法只有三种[1-3]：待定系数法、基函数法(Lagrange插值构造思想)、余项校正法(Newton插值的构造思想)，如n次的Newton插值多项式：

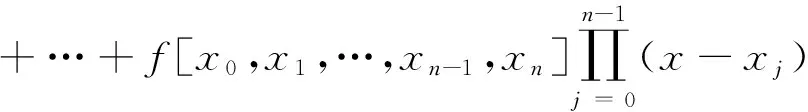
(1)

其中f[x0,x1,…,xk],k=1,2,…,n为函数f(x)的k阶差商，节点xi,i=0,1,2,…,n互不相同，且pn(x)满足插值条件

pn(xi)=f(xi),i=0,1,2,…,n.

1.2 范德蒙行列式

关于互不相同的实数xi,i=0,1,…,n的n+1阶的范德蒙行列式为

问题1[1]已知

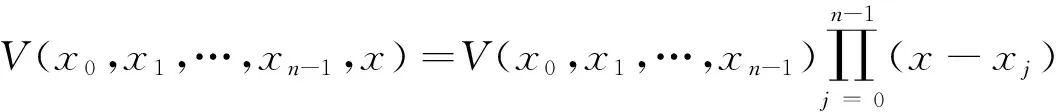
证明：由已知V(x0,x1,…,xn-1,x)是关于x的n次多项式，且

V(x0,x1,…,xn-1,xj)=0,j=0,1,…,n-1

将行列式按最后一行展开，知V(x0,x1,…,xn-1,x)的最高次项xn的系数为V(x0,x1,…,xn-1)，即得c=V(x0,x1,…,xn-1)，所以得(ⅰ)

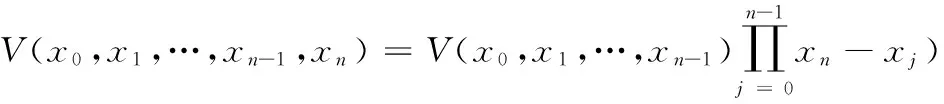
此证明恰恰利用了插值基函数的构造思想，即利用函数的零点及多项式的性质，从而使得范德蒙行列式的计算很简单！

范德蒙行列式的推广形式(范德蒙少列(行)的情形)的计算很多文献[4-7]都有研究，得出了不少的计算公式.文献中主要是利用对称多项式得出此行列式计算的递推公式，推导过程比较复杂，而且不易在计算机上实现计算.

在实际研究和教学中，发现一种类范德蒙行列式，也就是只有一列(行)与相应的范德蒙行列式不一样，针对它的计算，本文利用插值多项式给出了显示的计算公式，并且可以很方便地在计算机上实现其计算.

类范德蒙行列式定义如下：

(2)

即范德蒙行列式V(x0,…，xk)的第j+1列换成任意一组不全为零的实数yi,i=0,1,…,k，其中xi,i=0,1,…,k互不相同.

2 类范德蒙行列式的计算

问题2 计算行列式

的值，其中已知xi,i=0,1,2,…,k互不相同，n是非负整数.

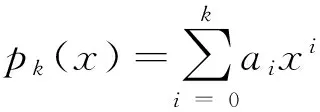
则由xi,i=0,1,2,…,k互不相同知

V(k,k)≠0⟹ak=V(k,n)/V(k,k);

而由Newton插值多项式(1)得

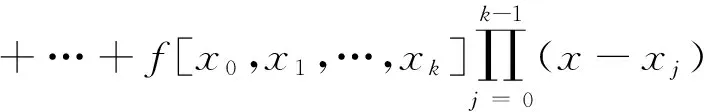
所以ak=f[x0,x1,…,xk]，则V(k,n)=f[x0,x1,…,xk]V(k,k).

由数学归纳法及差商的定义知…

所以

综合①②得

在具体的计算中，可以利用差商表编程计算出差商f[x0,x1,…,xk]，然后再计算V(k,n).

例1 计算行列式

解：令f(x)=x4，构造f(x)的差商表

2-24

3-3465

4-44120 55

则f[2,3,4]=55，所以V(2,4)=55×(3-2)(4-2)(4-3)=110.

问题3 计算行列式

的值，其中已知xi,i=0,1,2,…,k互不相同，yi,i=0,1,…,k是任意一组不全为零的实数.

则由xi,i=0,1,2,…,k互不相同知

V(k,k)≠0⟹aj=V(j)/V(k,k),j=0,1,…,k；

而由Newton插值多项式得

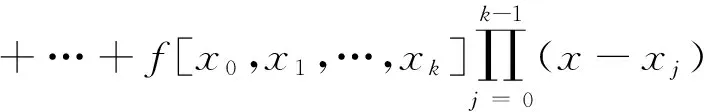
所以比较多项式pk(x)对应的xi,i=0,1,…,k系数，得

(3)

其中aj,j=0,1,…,k如(3)所示.

在具体的计算中，可以利用差商表编程计算出各阶差商及插值多项式，然后再计算V(j).

3 数值实例

例2 计算行列式

解：令f(2)=49,f(3)=142,f(4)=313,f(5)=586,f(6)=985，构造f(x)的Newton插值多项式为

p4(x)=49+93(x-2)+39(x-2)(x-3)+4(x-2)(x-3)(x-4)

则p4(x)=1+2x+3x2+4x3，

所以a3=4,得

V(3)=a3(3-2)(4-2)(5-2)(6-2)(4-3)(5-3)(6-3)(5-4)(6-4)(6-5)⟹V(3)=1152.

例3 计算行列式

解：令

f(0.3)=0.29850,f(0.4)=0.39646,f(0.5)=0.49311，f(0.6)=0.58813,f(0.7)=0.68122

构造f(x)的Newton插值多项式为

p4(x)=0.29850+0.97960(x-0.3)-0.06550(x-0.3)(x-0.4) -0.05333(x-0.3)(x-0.4)(x-0.5)+0.00833(x-0.3)(x-0.4)(x-0.5)(x-0.6)

则p4(x)=0.00026+0.99753x+0.00842x2-0.06833x3+0.00833x4，所以a1=0.99753，得

V(1)=a1(0.4-0.3)(0.5-0.3)(0.6-0.3)(0.7-0.3) ·(0.5-0.4)(0.6-0.4)(0.7-0.4)(0.6-0.5)(0.7-0.5)(0.7-0.6) ⟹V(1)=0.28728864×10-7

以上计算均是应用matlab编程实现.

[1] 王能超.计算方法简明教程[M].北京：高等教育出版社，2004 ：27-44.

[2] 何旭初,苏煜城，包雪松.计算数学简明教程[M].北京：人民教育出版社，1980:75-83.

[3] JOHN H. Mathews,Kurtis D. Fink(美国). Numerical methods using MATLAB fourth edition[M].北京：电子工业出版社，2005:161-177.

[4] 汤健儿，范舒羽.广义范德蒙行列式[J].高等数学研究，2010，(4)：48-49.

[5] 顾燕，张俊伟.范德蒙行列式的推广及其应用[J].大学数学，2015，(6)：72-76.

[6] 凌征球，廖珊莉，等.广义范德蒙行列式的定义及其计算[J].高师理科学刊，2015，(9)：5-7.

[7] 夏敏.范德蒙行列式推广形式的多项式证法[J].工科数学，1995，(1)：95 -98.

The Structure of the Interpolation Polynomial and the Computation of a Similar Vandermonde Determinant

SUN Yu-xiang， XU Yong

(College of Mathematics and Computer Science， Anhui Normal University， Wuhu 241000， China)

Using Newton interpolation polynomial and computation of divided-difference, an explicit computation formula of a similar vandermonde determinant is given; It is easy to calculate with computer.

interpolation polynomial; divided-difference; similar vandermonde determinant

10.14182/J.cnki.1001-2443.2016.06.003

2016-01-08

安徽省自然科学研究重点项目(KJ2016A268).

孙玉香(1964-)，女，安徽芜湖人，副教授.

孙玉香，许勇.插值多项式的构造与类范德蒙行列式的计算[J].安徽师范大学学报：自然科学版，2016，39(6)：521-525.

O241.6

A

1001-2443(2016)06-0521-05