非牛顿流体在多孔介质和霍尔电流效应下的几类精确解

张道祥， 程 航

(安徽师范大学 数学计算机科学学院,安徽 芜湖 241002)

非牛顿流体在多孔介质和霍尔电流效应下的几类精确解

张道祥， 程 航

(安徽师范大学 数学计算机科学学院,安徽 芜湖 241002)

非牛顿二阶流体的运动方程是一个高维的非线性微分方程,其精确解求解非常困难.本文利用逆方法求得非牛顿流体在多孔介质和霍尔电流效应下的几类精确解,所得的精确解有助于人们认识和理解非牛顿流体的流动特性.

非牛顿流体;逆方法;霍尔效应;多孔介质

由于经典的Navier-Stokes方程只能描述简单的非牛顿流体运动,为了解决复杂的非牛顿流体的运动,许多研究者将注意力集中在了非牛顿流体的研究上.最常见的求解非牛顿流体的方法就是Nemenyi提出的逆方法[1].逆方法是预先假设规定的涡量场或流场满足某种物理或者数学上的性质,再根据此求解其精确解.Taylor[2]通过假设涡量分布与流函数成正比,在牛顿流体中获得了随时间指数衰减的双无限涡列的精确解.Lin和Tobak[3]通过假设涡量与受到一个均匀流扰动的流函数成正比,运用逆方法解出了牛顿流体的精确解.Asghar[4],Labropulu[5],Siddiqui[6],张道祥,冯素晓[7]等利用逆方法获得二阶流体精确解.最近本文作者运用预设流函数求解偶应力流体的Riabouchinsky 型精确解[8].

受上述文章的启发,本文研究非牛顿流体在多孔介质和霍尔电流效应下的几类精确解.首先假设非牛顿流体的涡量分布满足

▽2ψ=A(ψ-Ux-BUy),

(1)

其中A,U,B都为常数且A≠0,U≠0.

1 基本方程

带有多孔介质和霍尔电流效应下的不可压缩二阶流体的控制方程为:

divV=0

(2)

(3)

其中V是速度向量,P为压力,ρ是常值密度,J是电流密度,B是总磁场,u是磁导率,E是总电场电流,K是多孔介质的渗透性,f是体力,T是Cauchy应力张量.

(4)

其中,u,α1,α2是可测量的物质常数,A1,A2为第一和第二阶Rivlin-Ericksen张量.

(5)

根据霍尔效应[9]有

▽·B=0,▽×B=umJ,▽×E=0,

(6)

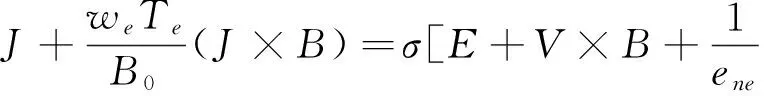
(7)

we是回旋频率,Te是电子碰撞时间,σ是导电性,e是总电子电荷,Pe是电子压力.将方程(4)-(7)代入方程(2)和(3),并且我们引入流函数ψ(x,y,t),它满足

代入方程(2)和(3)我们得到

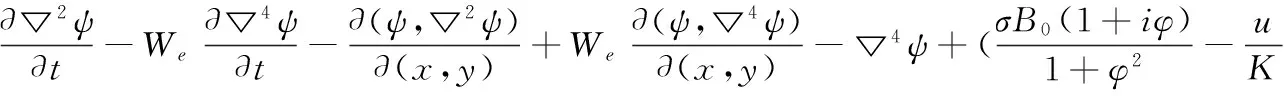
(8)

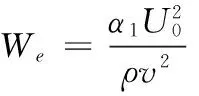
(9)

当1-WeA=0时,我们可以看出方程(9)变为ψ(x,y)=Ux+BUy,则u(x,y)=BU,v(x,y)=-U.

下面,我们考虑1-WeA≠0时定常和非定常下的精确解.

2 定常下的精确解

在定常条件下方程(9)变为

(10)

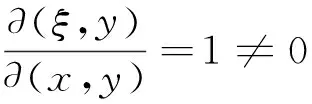
(11)

可以解出方程(11)的通解为

ψ=Uξ+eNyg(ξ)

(12)

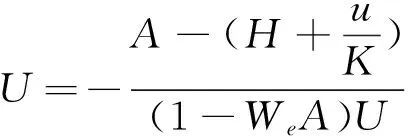
(1+B2)g″(ξ)+(B+BN)g′(ξ)+(N-A2)g(ξ)=0

(13)

此时的特征方程为

(1+B2)λ2+(B+BN)λ+(N-A2)=0

(14)

令Δ=(B+BN)-4(1+B2)(N-A2)

2.1Δ>0

此时,则

(15)

则g(x)的表达式为

g(ξ)=c1eλ1ξ+c2eλ2ξ

(16)

流函数和速度场为

ψ=Uξ+eNy(c1eλ1ξ+c2eλ2ξ)

(17)

u(x,y)=BU+NeNy(c1eλ1ξ+c2eλ2ξ)+BeNy(λ1c1eλ1ξ+λ2c2eλ2ξ)

(18)

v(x,y)=-U-eNy(λ1c1eλ1ξ+λ2c2eλ2ξ)

(19)

2.2Δ=0

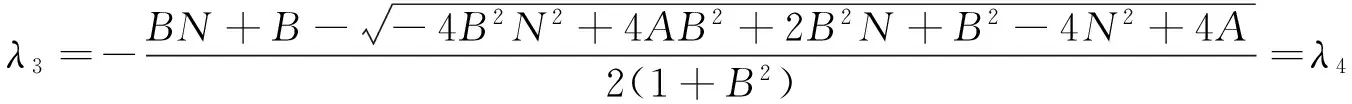
(20)

流函数和速度场为

ψ(x,y)=Uξ+eNy(c1+c2ξ)eλ3ξ，

(21)

u(x,y)=BU+NeNy(c1+c2ξ)eλ3ξ+Bλ1eNyeλ3ξ(c1+c2ξ)+c2BeNyeλ3ξ，

(22)

v(x,y)=-U-c2eNyeλ3ξ-λ1(c1+c2ξ)eNyeλ3ξ，

(23)

其中c1,c2为常数.

2.3Δ<0

流函数和速度场为

ψ(x,y)=Uξ+eNyeIξ(D1sinI2ξ+D2cosI2ξ)，

(24)

u(x,y)=BU+(N+BI1+BI2)eNyeI1ξ(D1sinI2ξ+D2cosI2ξ)，

(25)

v(x,y)=-U-(I1+I2)eNyeI1ξ(D1sinI2ξ+D2cosI2ξ)，

(26)

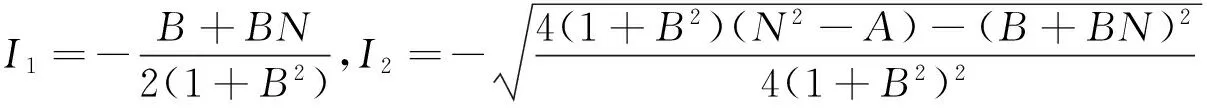
3 非定常下的精确解

在非定常情形下,因为1-WeA≠0,令B=0我们有

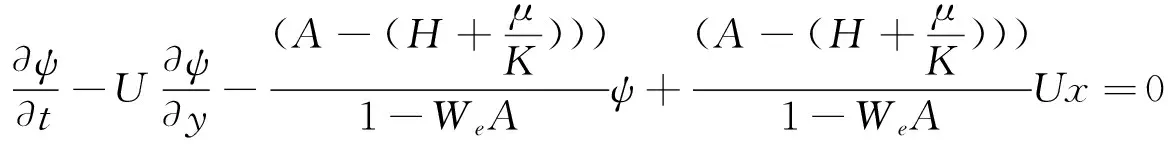
(27)

我们令ξ=y+Ut,y=y.

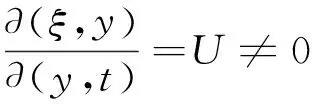
(28)

在新的坐标系下方程(28)转变为

(29)

我们可以得到

ψ=Ux+eNyg(ξ,x).

(30)

将(30)代入(1)中, 我们得到g(ξ,x)满足

(31)

关于方程(31), 我们令

g=G(η),η=ξcosθ+xsinθ，

(32)

θ为常数, 将(32)代入(31)

G″(η)+2NcosθG′(η)+(N2-A)G(η)=0,

(33)

我们假设(33)的解形式为G(η)=emη,我们有

m2+2Ncosθ+(N2-A)=0，

(34)

由方程(34)我们解出

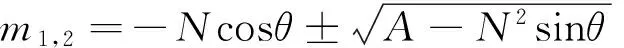
(35)

3.1A-N2sinθ>0

此时我们有

G(η)=A1em1η+A2em2η，

(36)

其中m1,m2在(35)中给出, 这时候流函数以及速度分别为

ψ(x,y,t)=Ux+eNy(A1em1η+A2em2η)，

(37)

u(x,y,t)=NeNy(A1em1η+A2em2η)+eNycosθ(A1m1em1η+A2m2em2η)，

(38)

v(x,y,t)=-U-eNysinθ(A1em1η+A2em2η)，

(39)

其中,A1,A2是常数.图1给出了当U=1,N=1,A1=1,A2=0,t=1,A=0.8,θ=0的流函数等值线.我们得到了带有垂向上有抽(吸)作用的平行流动.

图1 流函数的等值线

3.2A-N2sinθ=0

此时我们有

G(η)=e-Nηcosθ(D1+D2η)，

(40)

这时候流函数以及速度分别为

ψ(x,y,t)=Ux+eNy-Nηcosθ(D1+D2η)，

(41)

u(x,y,t)=eN(y-ηcosθ)[Nsin2θ(D1+D2η)+D2cosθ]，

(42)

v(x,y,t)=-U-eN(y-ηcosθ)sinθ[D2-D2cosθ(D1+D2η)]，

(43)

3.3A-N2sinθ<0

此时我们有

G(η)=e-Nηcosθ[E1sin(mη)+E2cos(mη)]，

(44)

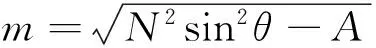
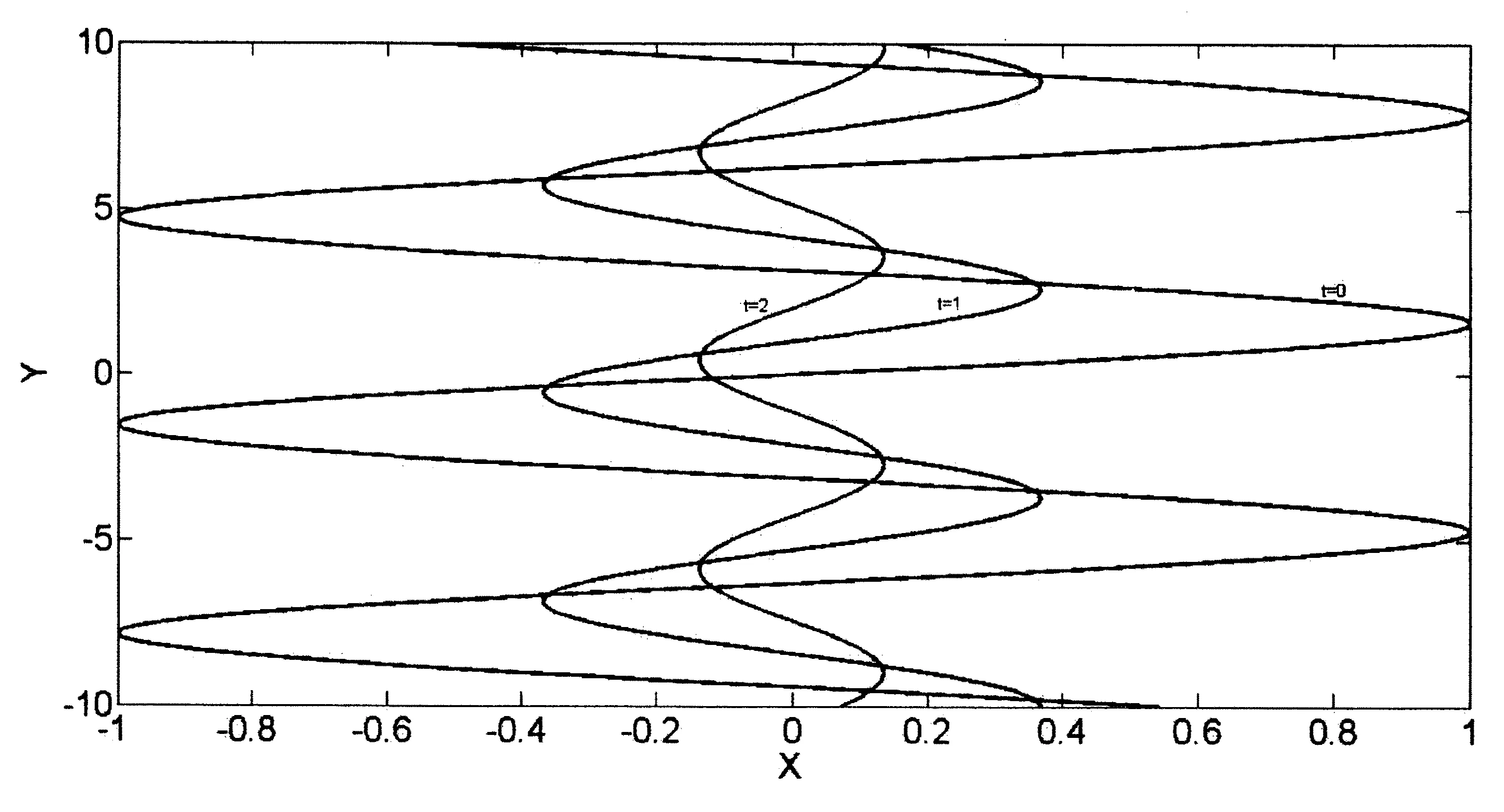
图2 流函数ψ(x,y,t)=-x+e-tsin(y-t)的等值线

ψ(x,y,t)=Ux+eN(y-ηcosθ)[E1sin(mη)+E2cos(mη)]

(45)

u(x,y,t)=eN(y-ηcosθ)Nsin2θ[E1sin(mη)+E2cos(mη)] +eN(y-ηcosθ)mcosη[E1sin(mη)-E2cos(mη)]，

(46)

v(x,y,t)=-U-eN(y-ηcosθ)sinθm[E1cos(mη)-E2sin(mη)] +eN(y-ηcosθ)sinθNcosθ[E1cos(mη)-E2sin(mη)]．

(47)

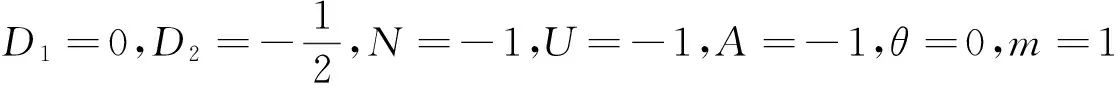
4 结论

非牛顿流体的精确解目前仍是力学和数学研究者关注的热点问题.本文在预设涡量场分布的条件下,研究在多孔介质和霍尔电流效应下定常和非定常情形下二阶流体的精确解.我们得到了带有垂向上有抽(吸)作用的平行流动以及随着时间按指数衰减的流动精确解.

[1]NEMENYIPF.Recentdevelopmentsininverseandsemi-inversemethodsinthemechanicsofcontinua[J]. Advance in Applied Mechanics, 1951,2(11):123-151.

[2] TAYLOR G T. On the decay of vortices in a viscous fluid[J]. Phil Mag, 1923,(46):671-674.

[3] LIN S P, TOBAK M. Reversed flow above a plate with suction[J]. AIAA, 1986,(24):334-335.

[4] HAYAT T, MOHYUDDIN M R, ASGHAR S. Some inverse solutions for unsteanian fluid[J]. Tamsui Oxford Journal of Mathematical Sciences, 2005,21(1):1-20.

[5] LABROPULU F. Exact solutions of non-Newtonian fluid flows with prescribed vorticity[J]. Acta Mechanics,2000,(141):11-20.

[6] SIDDIQUI A M, MOHYUDDIN M R, HAYAT T, ASGHAR S. Some more inverse solutions for steady flows of a second-grade fluid[J]. Arch Mech, 2003,(55):373-387.

[7] 张道祥,冯素晓.二阶非牛顿流行蠕流精确解[J].力学季刊, 2008,29(3):418-423.

[8] 张道祥,程航.偶应力流体的Riabouchinsky型精确解[J].安徽师范大学学报:自然科学版,2005,38(5):414-418.

[9] Muhammad R Mohyuddin, Ehsan Ellahi Ashraf. Inverse solutions for a second-grade fluid for porous medium channel and Hall current effects[J]. Indian Acad Sci, 2004,1(114):79-96.

Some Certain Exact Solutions of Non-Newtonian Fluid for Porous Medium Channel and Hall Current Effects

ZHANG Dao-xiang, CHENG Hang

(College of Mathematics and Computer Science, Anhui Normal University, Wuhu 241002, China)

The equations of non-Newtonian second-grade fluid flow are highly nonlinear partial differential equations. This paper aims to investigate analytical solutions of non-Newtonian fluid for porous medium channel and Hall current effects via inverse method for steady and unsteady cases. The exact solutions help us to understand the flow characteristics of non-Newtonian fluids.

non-Newtonian fluid; inverse method; Hall effects; porous medium

10.14182/J.cnki.1001-2443.2016.06.002

2015-10-20

国家自然科学基金青年项目(11302002).

张道祥(1979-)，男，安徽天长市人，副教授，博士.

张道祥，程航.非牛顿流体在多孔介质和霍尔电流效应下的几类精确解[J].安徽师范大学学报：自然科学版，2016，39(6)：516-520.

O175

A

1001-2443(2016)06-0516-05