基于组合设计框架的无线传感器网络密钥预分配方案

吴苗苗，张勇，曹瑞峰

（盐城师范学院数学与统计学院，江苏盐城224002）

基于组合设计框架的无线传感器网络密钥预分配方案

吴苗苗，张勇*，曹瑞峰

（盐城师范学院数学与统计学院，江苏盐城224002）

本文研究了基于超单纯平衡不完全区组设计的无线传感器网络的密钥预分配方案。主要采用了基于部分平衡t设计的组合研究框架，运用matlab仿真方法对该方案的基本度量进行计算和分析，发现该方案与基于指数为1的平衡不完全区组设计的方案相比，保持了连通性，适当牺牲了弹性，但获得了更大的实用性。

无线传感器网络；密钥预分配方案；部分平衡t设计；BIBD

无线传感器网络是由若干个具有有限存储能力、有限能量和有限计算能力的小的传感器节点组成的自适应网络。节点间能够彼此通信来积累信息，并以安全的方式将其传递给基站。由于这种通信通常发生在敌对区里，因此需要对信息进行加密或认证。公钥密码方案由于其计算量大以及昂贵的计算成本，因此不适宜作为加密方案。通常采用密钥预分配方案(KPS)，即在节点分发前将安全密钥预先安装在每个传感器节点上。影响KPS的主要因素(基本度量)有网络规模、存储要求、网络连通性和网络弹性。设计一个好的KPS方案的根本问题是如何平衡上述指标。

现有基于组合设计的KPS方案[1-3]中，Paters on和Stinson引入了部分平衡t设计的概念，建立了无线传感器网络的密钥预分配方案的组合研究框架[1]。指数为1的平衡不完全区组设计(BIBD)[4]作为部分平衡2设计有较好的弹性和连通性，但指数的限制使其在实际使用中有一定局限性。超单纯BIBD是一类指数大于1且无重复区组的设计，因为它与相同参数的一般平衡不完全区组设计相比，能使被区组覆盖的三元组的个数尽可能大，所以本身有重要的理论价值，同时它在编码和密码中有重要应用。本文提出用超单纯BIBD构造KPS方案，并分析其性能。

1 基于区组设计的KPS方案

一个组合设计(或称为区组设计)是一个二元组（X，H），其中X为有限点集，H是X的子集族，称为区组集，称为A∈H区组，其所含元素个数称为区组长度。若所有区组的长度是定值k，则称（X，H）是k阶一致的。对于x∈X，包含x的区组数称为x的次数。若所有点的次数是定值r，则称（X，H）是r次正则的。

如果一个传感器网络由b个传感器节点U1，…，Ub和v个密钥key1，…，keyv组成，那么可采用区组设计（X，H），X={xi∶1≤i≤v}，H={Aj∶1≤j≤b}。节点Uj（1≤j≤b）接收密钥子集{keyi∶xi∈Aj}中的密钥，xi充当keyi的身份标识，这样就建立了一个基于区组设计的KPS方案。并非所有的区组设计都可用作KPS方案，能用作KPS方案的区组设计被称为部分平衡t设计。

2 部分平衡t设计及其度量

定义1[1]令v，k，t是正整数，λ0，λ1，…，λt-1也是正整数。设（X，H）是v元集X上的一个含有λ0个区组的k阶一致的区组设计，称（X，H）为t-（v,k,λ0，…，λt-1）部分平衡t设计(PB t D)，如果满足：

(1)对于1≤i≤t-1，每个i子集出现在0个区组或者λi个区组中；

(2)对于t≤i≤k，每个i子集出现在0个或1个区组中。

网络连通性和弹性通常分别记为Pr1和fail(1)。

引理1[1]对给定的无线传感器网络，若采用相交门限为η的t-（v，k，λ0，…，λt-1）-PB t D作为KPS方案，则有

在基于PB t D的KPS方案的框架下可以方便地引入基于超单纯BIBD的KPS方案。

3 基于超单纯BIBD的KPS方案

设有v元集X上的一个含有b个区组的r次正则的k阶一致的区组设计（X，H），若X中每一对不同的元素恰好在H的λ个区组中相遇，则称（X，H）是一个（v，k，λ）平衡不完全区组设计，简记为（v，k，λ）-BIBD。容易看出，（v，k，1）-BIBD是部分平衡2设计(PB2D)，因此（v，k，1）-BIBD可以用作KPS方案。但是，当λ＞1时，一个（v，k，λ）-BIBD未必是一个PB t D。例如，将一个（v，k，1）-BIBD的所有区组重复1次，得到一个（v，k，2）-BIBD，这就不是一个PB t D。因此，已有的相关方案都限定λ=1[1-3]。但是，并不是对任意节点的传感器网络都存在一个区组数等于网络节点数的（v，k，1）-BIBD，所以需要研究指数大于1的BIBD作为KPS方案。

如果区组集中没有重复区组，一个（v，k，λ）-BIBD称为单纯的；如果区组集中任意两个区组至多相交于两个公共点，则称为超单纯的。超单纯（v，k，λ）-BIBD记为（v，k，λ）-SSBIBD。当k=3时，单纯设计也是超单纯；λ=1的设计一定是超单纯设计。本文仅涉及k=4的超单纯设计。对于（v，4，λ）-SSBIBD，其参数满足vr=4b以及3r=λ（v-1），因此由引理1得如下定理。

定理1对于基于（v，4，λ）-SSBIBD的KPS方案，Pr1和fail(1)为

对于一个（v，k，λ）-BIBD，（X，H），取X为Zv，即模v的剩余类环，则σ∶i→i+1（mod v）是Zv上的一个置换。如果v整除b，且在H中存在b/v个区组，在σ的作用下可得到所有区组，称（X，H）是循环的，记为（v，k，λ）-CBIBD，b/v个区组称为基区组。超单纯（v，k，λ）-CBIBD简记为（v，k，λ）-SSCBIBD。

分别以相遇数为1，2和4的SSCBIBD为例说明SSBIBD的度量，后面将以这些例子为基础分析一般的SSBIBD的性能。

例1(13,4,1)-SSCBIBD如表1。

表1 (13,4,1)-SSBIBD

这里v=13，k=4。将基区组模加1展开后得所有13个区组，所以b=λ0=13。计算得r=λ1=4，λ=λ2=1。根据定义，这是一个2-（13，4，13，4）-PB2D。由定理1得

例2(13,4,2)-SSCBIBD如表2。

表2 (13,4,2)-SSBIBD

这里v=13，k=4。将基区组模加1展开后得所有26个区组，所以b=λ0=26。计算得，

根据定义，这是一个3-（13，4，26，8，2）部分平衡3设计(PB3D)。由定理1得

例3(10,4,4)-SSCBIBD如表3。

表3 (10,4,4)-SSBIBD

这里v=10，k=4。将基区组模加1展开后得所有30个区组，所以b=λ0=30。计算得，

根据定义，这是一个3-（10，4，30，12，4）-PB3D设计。由定理1得

4 方案的性能分析

首先，关于连通性，对于（v，4，λ）-BIBD而言，由定理1知Pr1恒为1，所以基于超单纯BIBD的KPS方案保持了连通性。

其次，关于弹性，运用Matlab软件画图，以区组数b为自变量，fail（1）为因变量，（v，4，1）-BIBD与（v，4，2）-SSBIBD的fail（1）的对比见图1。

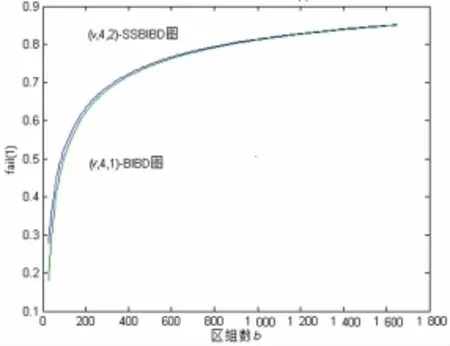
图1 fail(1)对比图，指数为1和2

图1 表明，随着区组数的增加，（v，4，2）-SSBIBD比（v，4，1）-BIBD的弹性稍低，但非常接近。

（v，4，2）-SSBIBD与（v，4，4）-SSBIBD的fail(1)的对比如图2。从图中看出，随着区组数的增加，（v，4，2）-SSBIBD比（v，4，4）-SSBIBD的弹性稍好，但非常接近。

图2 fail(1)对比图，指数为2和4

以节点数v为自变量，fail（1）为因变量，（v，4，2）-SSBIBD与（v，4，4）-SSBIBD的fail（1）比较见图3。

图3 （v,4,2）-SSBIBD与（v,4,4）-SSBIBD的fail（1）对比图

从图3看出，随着节点个数的增加，（v，4，2）-SSBIBD比（v，4，4）-SSBIBD的弹性稍好，但非常接近。

在弹性性能方面，从上述几个例子的计算结果以及图像来看，随着λ的增大，fail（1）的值逐渐增加，弹性有所降低但非常接近，与其他设计的结果差距较小。

最后，要指出基于SSBIBD的KPS方案具有更大的实用性。例如，（v，4，1）-BIBD存在的条件是v≡1,4（mod12），而（v，4，2）-SSBIBD和（v，4，4）-SSBIBD存在的条件是v≡1（mod 3），而（v，4，6）-SSBIBD存在的条件是v是不小于14的整数，所以超单纯设计使得无线传感器网络的密钥数目v选择更为自由。同样，超单纯设计也使得传感器的节点数目b的选择更为自由。因此，基于超单纯平衡不完全区组设计的KPS方案更为实用。

5 SSBIBD的存在性

以（v，4，λ）-SSBIBD为例，说明存在为数众多的SSBIBD，从而说明基于SSBIBD的KPS方案更具有实用性。对于任意k，λ必要条件也是渐进充分的[5]。对于（v，4，λ）-SSBIBD，当λ=2，3,4,5,6,8,9时，一个（v，4，λ）-SSBIBD存在的必要条件也是充分的[2,6-15]。

命题1[2,5-15]对于λ=2,3,4,5,6,8,9,当且仅当v和λ满足表4中所列的条件时存在一个（v，4，λ）-SSBIBD。

表4 （v，4，λ）-SSBIBD存在的条件

命题2[15]对λ=2,3,4于,当且仅当v和λ满足表5所列条件时存在一个超单纯（v，4，λ）-SSCBIBD。

表5 （v，4，λ）-SSCBIBD存在的条件

更多结果请参考文献[4]及相关文献。

6 总结

总之，使用超单纯BIBD的无线传感器网络的KPS方案与基于λ=1的BIBD的KPS方案相比，保持了原有的连通性，适当的牺牲了弹性，但同时换来了更大的实用性。文章还举例说明了存在大量的SSBIBD，这在使用上是很方便的，该方案丰富了基于区组设计的KPS方案理论。

[1]PATERSON M B,STINSON D R.A unified approach to combinatorial key predistribution schemes for sensor networks[J]. Designs,Codesand Cryptography,2014（3）：433-457.

[2]LEE J,STINSON D R.On the construction of practical key predistribution schemes for distributed sensor networks using combinatorial designs[J].ACM Transactions on Information and System Security,2008,11(2):1-35.

[3]DENG W,DU J,HAN Y,et al.A pairwise key predistribution scheme forwireless sensor networks[J]．ACM Transactions on Information and System Security,2005，8:228-258.

[4]COLBOURNC J,DINITZ JH.Handbook of combinatorial designs [M].2nd Edition.Boca Raton:Chapman and Hall/CRC,2007.

[5]GRONAU H D O F,MULLIN R C.On super-simple 2-(v,4,λ) designs[J].JournalofCombinatorialMathematicsand Combinatorial Computing,1992，11:113-121.

[6]KHODKAR A.Various super-simple designswith block size four [J].The Australasian Journalof Combinatorics,1994，9:201-210.

[7]BLUSKOV I,HEINRICH K.Super-simple designswith v<=32[J]. JournalofStatisticsand Planning Inference,2001，95:121-131.

[8]CHEN K.On the existence of super-simple(v,4,3)-BIBDs[J]. Journal of Combinatorial Mathematics and Combinatorial Computing，1995，17:149-159.

[9]CHEN K.On the existence of super-simple(v,4,4)-BIBDs[J]. Journalof Statisticsand Planning Inference，1996，51:339-350.

[10]CHEN K,CAO Z,WEIR.Super-simple balanced incomplete block designswith block size4 and index 6[J].Journalof Statistics and Planning Inference，2005，133：537-554.

[11]CHEN K,WEIR.Super-simple cyclic designswith small values [J].Journal of Statistics and Planning Inference，2007，137：2034-2044.

[12]CAO H,CHEN K,Wei R.Super-simp le balanced incomp lete block designs with block size 4 and index 5[J].Discrete Mathematics，2009，309：2808-2814.

[13]ZHANG Y,CHEN K,SUN Y G.Super-simp le balanced incompleteblock designswith block size4 and index9[J].Journal of Statisticsand Planning Inference，2009，3139：3612-3624.

[14]CHEN K,SUN Y G，ZHANG Y.Super-simple balanced incomplete block designs with block size 4 and index 8[J]. UtilitasMathematics，2013，91：213-229.

[15]周海萍,曹海涛.超单严格循环设计的一些结果[J].数学年刊A辑（中文版），2010（4）：427-442.

Key Predistribution forWirelessWensor NetworksBased on a Classof Combinatorial Design

WU Miao-miao，ZHANG Yong，CAO Rui-feng
(School of Mathematics and Statistics，Yancheng Teachers University，Yancheng，Jiangsu 224002，China)

The paper studies the key predistribution schemes of the wireless sensor networks based on super simple balanced incomplete block design.The combinatorial frame is adoped，which is established based on partially balanced tdesign.MATLAB simulation analysis and computation of the basic metric of this scheme,prove that the schememaintains the original connectivity,slightly sacrifice the flexibility but in exchange for greater practicality compared with KPS based on balanced incomplete block design which index is equal to 1.

wireless sensor networks；key predistribution scheme；partially balanced t-design；BIBD

O157.2

A

1007-4260(2016)04-0053-04

时间：2017-1-3 17:19

http://www.cnki.net/kcms/detail/34.1150.N.20170103.1719.015.html

2016-04-28

江苏省高等学校大学生创新创业训练项目（201410324039Y，201410324058X）。

吴苗苗，女，江苏连云港人，盐城师范学院数学与统计学院硕士研究生，研究方向为传感器网络。

E-mail:1125098835@qq.com

张勇，男，江苏盐城人，博士，盐城师范学院数学与统计学院副教授，研究方向为组合设计。E-mail:zyyctu@gmail.com

10.13757/j.cnki.cn34-1150/n.2016.04.015