预给极点的连分式插值
2016-02-11张澜赵前进
张澜,赵前进
(安徽理工大学理学院,安徽淮南232001)
预给极点的连分式插值
张澜,赵前进
(安徽理工大学理学院,安徽淮南232001)
本文给出一种预给极点的连分式插值算法。通过每个插值函数值乘以一个确定的数,将预给极点的插值转化为无预给极点的插值,基于逆差商构造Thiele型连分式插值,最终通过除以一个确定的函数获得预给极点的连分式插值,具有预给的极点且极点保持原有的重数。数值实例验证了新方法的优点。
连分式;插值;预给极点;重数;逆差商
在工程实践和科学研究领域存在大量有极点的奇异函数的计算问题,连分式插值与逼近是解决此类问题的有效途径之一[1-6]。基于连分式的Thiele型连分式插值是一种多见的有理函数插值,Thiele型连分式容易计算,所以在实际问题中应用十分广泛[7-11]。朱功勤等[1]提出了一个计算预给极点的二元向量有理插值方法,通过设定极点处的向量函数值为无穷大向量以及基于向量的Samelson逆来计算预给极点的二元向量有理插值,但是无法区分和保持极点的重数。本文研究预给极点的连分式插值。
1 连分式插值
设点集X={x0,x1,…,xn}⊂[a,b],函数f(x)在[a,b]上有定义。X上的Thiele型连分式插值[2]为
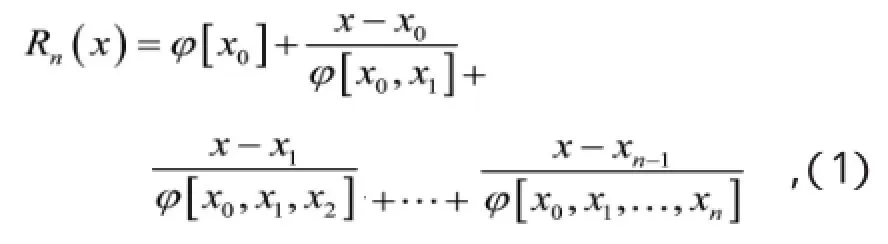
其中φ[x0,x1,…,xk]为f(x)在x0,x1,…,xk处的k阶逆差商,递推定义如下,
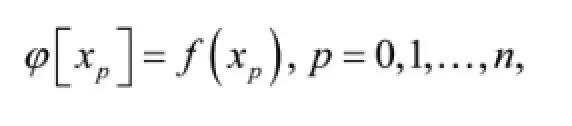
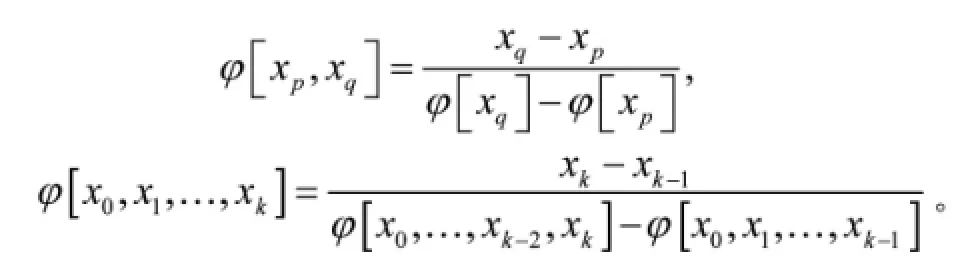
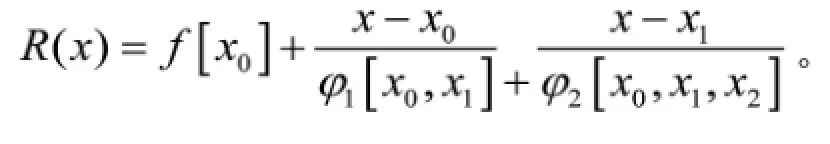
设x0,x1,…,xn是在区间[a,b]上n+1个不同的插值节点,fi=f(xi),i=0,1,…,n是被插值函数f(x)在这些节点处对应的函数值。
2 预给极点的连分式插值
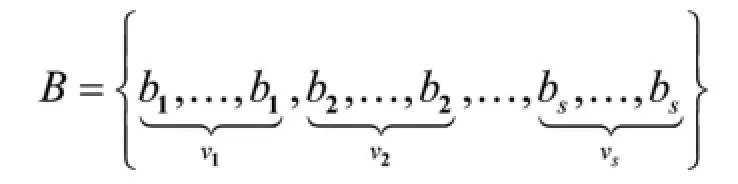
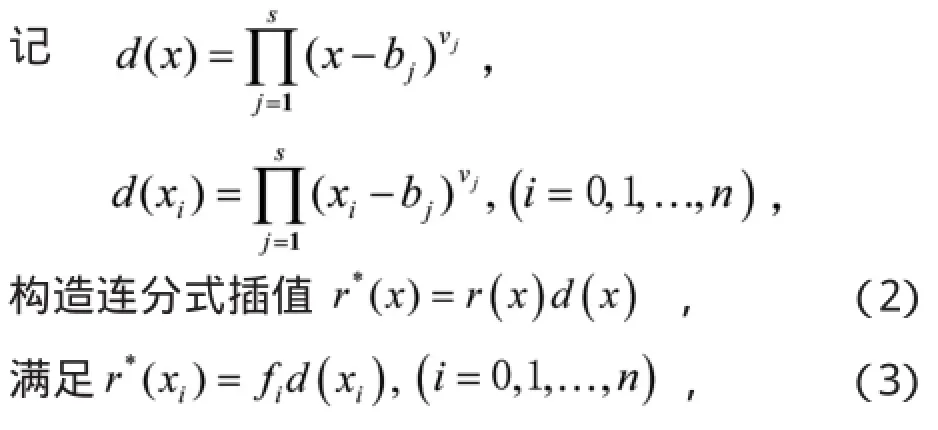
基于逆差商,计算得满足(3)式的Thiele型连分式插值函数r*(x),从而得到预给极点的连分式插值

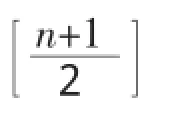
3 数值例子

计算得Thiele型连分式插值函数

显然,当r(x)的分子、分母多项式在各极点处的值均不等于零时,有理插值函数不仅存在r(x)预给的极点,而且每个预给极点保持原有的重数。
朱功勤等[13]中提出计算预给极点的有理插值方法,通过设定极点处的函数值为无穷大,将预给极点结合原有的插值节点都作为新的插值节点。这里设定在x0=0和x6=1处,f(x0)和f(x6)取无穷大,那么由文献[13]的方法得到Thiele型连分式插值函数

此方法虽然能够求出插值函数,但是无法区分和保持极点的重数。
给出不同的插值节点在不同的插值函数处的取值以及误差,如表1所示。
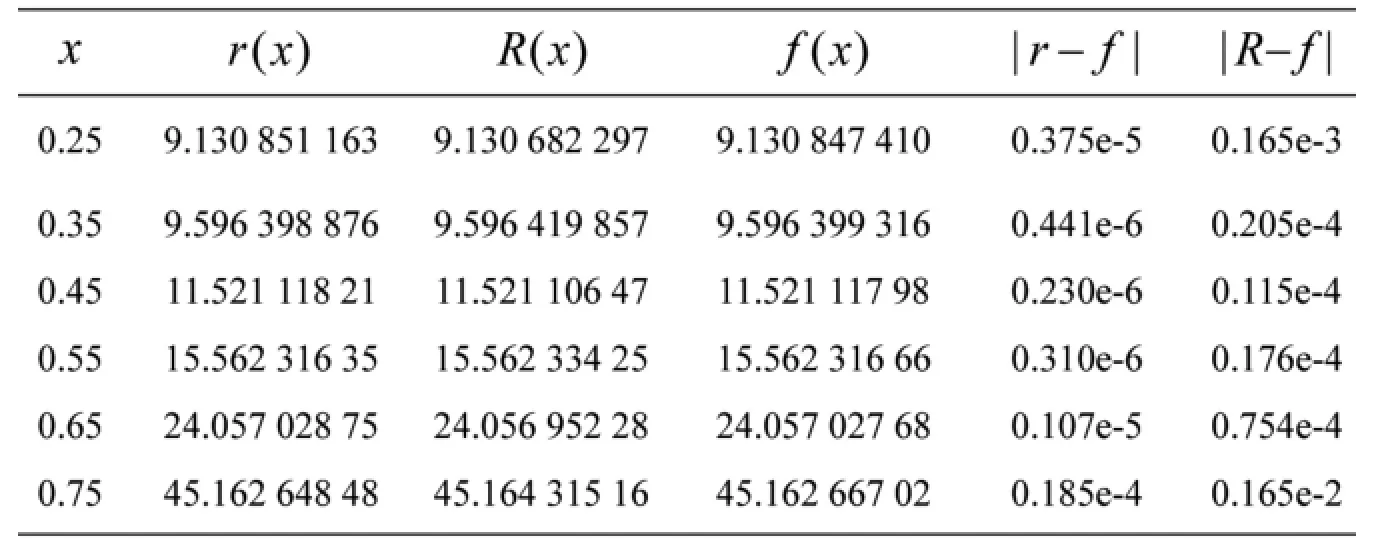
表1 误差分析
经过比较发现│r-f│<│R-f│,验证了新方法的优点。
也可以通过对两种连分式插值函数的定积分结果进行对比分析,如表2所示。

表2 定积分结果分析
上述数值例子验证了预给极点的连分式插值方法误差较小。
4 结论
通过每个插值函数值乘以一个确定的数,将预给极点的插值转化为常规的无预给极点的插值,进一步基于逆差商来计算Thiele型连分式插值,最终再通过除以一个确定的函数获得预给极点的插值函数,它具有预给的极点且每个预给极点保持原有的重数。给出的数值实例说明了新方法的优点。
[1]朱功勤,檀结庆,王洪燕.预给极点的向量有理插值及性质[J].高等学校计算数学学报,2000,22(2):97-104.
[2]檀结庆.连分式理论及其应用[M].北京:科学出版社,2007: 90-130.
[3]TAN J Q,FANG Y.Newton-Thiele's rational interpolants[J]. NumericalAlgorithms,2000,24(1-2):141-157.
[4]TAN JQ.Bivariate blending rational interpolants[J].Approx Theory &Its Appl,1999,15(2):74-83.
[5]ZHAO Q J,TAN JQ.Block-based Thiele-like blending rational interpolation[J].Journalof Computational&Applied Mathematics, 2006,195(1-2):312-325.
[6]LUDW,SONG ZX.Some new continued fraction estimatesof the Somos'quadratic recurrence constant[J].JournalofNumber Theory, 2015,155:36-45.
[7]LORENTZEN L.A convergence theorem for random continued fractions[J].Journalof Approximation Theory,2014,197:1-8.
[8]FANG L,WU M,SHIEH N R,etal.Random continued fractions: Lévyconstantand Chernoff-typeestimate[J].Journal of Mathematical Analysis&Applications,2015,429(1):513-531.
[9]CUYT A,VERDONK B.Multivaite rational interpolation[J]. Computing,1985,34:141-161.
[10]CUYTA,VERDONK B.Different Techniques for the Construction of Multivariate ational Interpolants[M].Nonlinear Numerical Methods and RationalApproximation:Springer Netherlands,1988: 167-190.
[11]CUYT A,VERDONK B.Multivariate reciprocal differences for branched Thiele continued fraction expansions[J].Journal of Computational&App lied Mathematics,1988,21(2):145-160.
[12]BERRUT JP.The barycentric weights of rational interpolation with prescribed poles[J].Journalof Computational&App lied Mathematics,1997,86(1):45-52.
[13]王仁宏,朱功勤.有理函数的逼近以其应用[M].北京:科学出版社,2004:139-142.
Continued Fraction Interpolation with Prescribed Poles
ZHANG Lan,ZHAOQian-jin
(College of Science,Anhui University of Science&Technology,Huainan,Anhui 232001,China)
An algorithm is given to calculate the continued fraction interpolant with prescribed poles.By means of multiplying each interpolated value by a certain number,interpolation with prescribed poles is transformed into the one without prescribed poles.The Thiele-type continued fraction interpolant is constructed based on inverse differences.Finally,the continued fraction interpolant with prescribed poles is obtained and has been prescribed poles with intrinsic multiplicity.An example is given to show the advantage of the newmethod.
continued fraction;interpolation;prescribed poles;multiplicity;inverse differences
O241.3
A
1007-4260(2016)04-0008-03
时间:2017-1-3 17:19
http://www.cnki.net/kcms/detail/34.1150.N.20170103.1719.003.html
2016-06-15
国家自然科学基金(60973050)和安徽省教育厅自然科学基金(KJ2009A50)。
张澜,女,河南南阳人,安徽理工大学理学院硕士研究生,研究方向为有理插值与逼近,数字图像处理。
E-mail:zhanglan0703@163.com
10.13757/j.cnki.cn34-1150/n.2016.04.003
