一类半线性椭圆型偏微分方程组边值问题的可解性研究

吴乐，钟金标

（安庆师范大学数学与计算科学学院，安徽安庆246133）

一类半线性椭圆型偏微分方程组边值问题的可解性研究

吴乐，钟金标*

（安庆师范大学数学与计算科学学院，安徽安庆246133）

利用不动点定理研究了椭圆型方程组边值问题的可解性，针对非线性项关于在无穷远处和零点处为次线性与超线性情形，讨论了一类半线性椭圆型方程组解的存在性。

不动点定理；紧正算子；Green函数

近几十年来，非线性偏微分方程（组）是现代微分方程研究的重中之重，在解决物理学、生态学、气动力学等领域问题中起着重要的作用。但是非线性偏微分方程求解难度很大，一直以来数学工作者们都致力于研究解决非线性偏微分方程（组）的行之有效的方法[1-4]，其中，钟金标[1]运用变分原理深入研究了以下边值问题

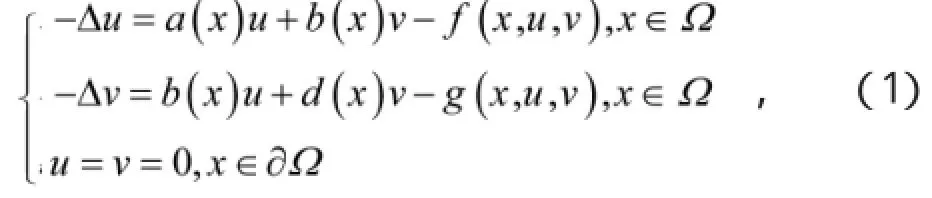
的解的存在性。受此启发，本文主要利用不动点定理研究问题

解的可解性，其中a（x），b（x），c（x），d（x）∈C0（Ω，R），Ω⊆RN(N≥2)是一个有界光滑区域。本文研究的问题（2）中非线性项b（x）与c（x）不要求相等，因而比问题（1）更具有一般性。对问题（2）中f（x，s，t），g（x，s，t）关于s，t在∞处和零点处为次线性和超线性两种情形，利用不动点理论分别证明其解的存在性。

给定条件：

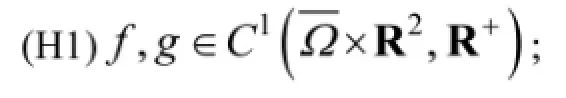
这里记‖wn‖=max｛‖un‖,‖vn‖｝，其中-△算子在有界光滑区域Ω中0-Dirichlet边值问题的第一特征值记为λ1，则λ1＞0，与其对应的特征函数φ1在Ω中是正函数。记

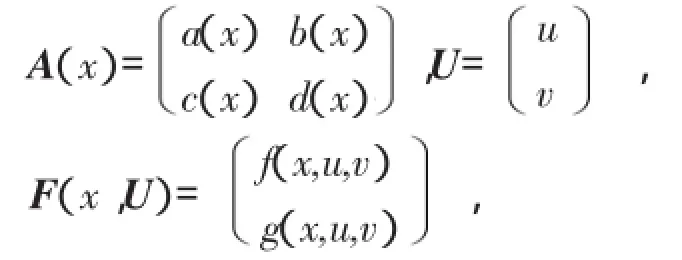
则（2）式可表示为向量方程边值问题

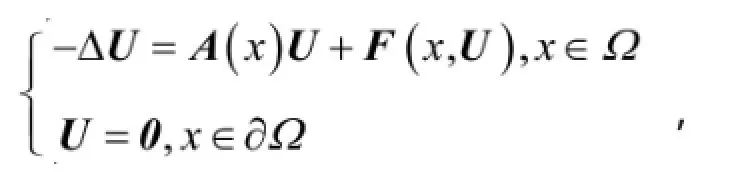
解的存在性。

引进范数:

参考文献:

[1]SILVA E D D.Multiplicity for gradient systems with strong resonanceathighereigenvalues[J].Nonlinear Analysis,2010，72：3918-3928.

[2]ZHONG Jinbiao，CHEN Zuchi.Existence and uniqueness of positive solutions to a class of semilinear elliptic systems[J].Acta Mathematica Scientia，2002，22(4)：451-458.

[3]钟金标，陈祖墀.一类拟线性方程组的可解性[J].应用数学学报,2003,26(3):420-426.

[4]ZHONG Jinbiao，CHEN Zuchi.Existence and nonexistence of positive radialsolutions for a classof semilinear elliptic systems[J]. SystemsScienceand Complexity，2004，17（3）:325-331.

[5]DELIMLINGK.Nonlinear foundationalanalysis[M].Berlin:springer, 1985.

[6]GILBARG D,TRUDINGER N S.Elliptic Partial Differential Equationsofsecond Order[M].2nd ed.Berlin:Springer,1983.

Solvability for Boundary Value Problemsof a Classof Semilinear Elliptic Equation System

WU Le，ZHONG Jin-biao
(School ofMathematics and Computational Science,Anqing Normal University,Anqing,Anhui246133,China)

In this paper,the Boundary value problems of semilinear elliptic system is discussed.According to nonlinear terms with sub-linear and super-linear in the infinity and zero point,the existence of solutions for two kinds of semi-linear elliptic systems have been proved by using the fixed point theorem.

fixed point theorem；compact and positive operator；Green function

O175.25

A

1007-4260(2016)04-0001-04

时间：2017-1-3 17:19

http://www.cnki.net/kcms/detail/34.1150.N.20170103.1719.001.html

2016-03-26

吴乐，女，安徽桐城人，安庆师范大学数学与计算科学学院硕士研究生，研究方向为偏微分方程。E-mail：1223343647@qq.com

钟金标，男，安徽安庆人，博士，安庆师范大学数学与计算科学学院教授，硕士生导师，研究方向为偏微分方程。

E-mail：zjb@aqnu.edu.cn.

10.13757/j.cnki.cn34-1150/n.2016.04.001