应用自回归条件异方差模型研究我国水力发电量
2016-02-11卢维学杨世娟鲍志晖
卢维学,杨世娟,鲍志晖
(黄山学院数学与统计学院,安徽黄山245041)
应用自回归条件异方差模型研究我国水力发电量
卢维学,杨世娟,鲍志晖
(黄山学院数学与统计学院,安徽黄山245041)
为了研究水力发电量条件方差的变化规律及残差的统计分布特征,引入自回归条件异方差模型,建立基于正态分布假设的同阶自回归条件异方差模型对我国2001年1月到2016年2月的水力发电量进行实证分析,研究得出该模型对发电量的估计与预测具有良好的效果。
自回归条件异方差;GARCH模型;水力发电量;正态分布
我国水能资源丰富,不仅在水能资源的蕴藏量上位居世界第一,而且对于开发的水能资源,也处于世界第一位。水电是目前第一大清洁能源,提供全世界大于1/5的电力。水力发电又是进行水资源综合开发、治理、利用、节能减排的一个组成部分。但是目前全国水力发电量仅占技术可开发利用量的13%左右,我国水能开发率在30%左右,水力发电前景广阔[1]。因此有必要对全国水力发电量进行分析预测。
自回归条件异方差(ARCH)模型[2]是由Robert Engle最早提出的,该类模型具有良好的统计特性及对波动现象的准确描述。ARCH模型通常用于对主体模型的随机扰动项进行建模,进而能够更充分提取残差中有用的信息,使得模型最终残差是白噪声的。自回归条件异方差模型在各个领域的应用都十分广泛[3-6],本文应用此模型对我国水力发电量进行实证分析。
1 ARCH模型
1.1 模型介绍
对于通常的回归模型:


其中ηt独立且同分布,并同时满足Eηt=0,Dηt=λ2,则称(2)式为自回归条件异方差模型,简记εt~ARCH(q),(1)式和(2)式组合构成回归-ARCH模型。若已知εt~ARCH(q),则对于AR(p)模型yt=φ1yt-1+φ2yt-2+…+φpyt-p+εt也可以用AR(p)-ARCH(q)模型进行描述。
1.2 ARCH效应检验
检验时间序列是否存在ARCH效应,最常用的是拉格朗日乘数检验法(LM检验)。若模型的随机扰动项εt~ARCH(q),进而建立回归方程:
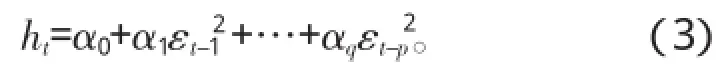
检验序列是否具有ARCH效应,只需检验(3)式中的各个回归系数α0,α1,…,αq是不是同时为0,若同时为0,说明不存在ARCH效应。对此给出检验的原假设与备择假设分别为H0∶α0=α1=…=αq=0;H1∶α0,α1,…,αq至少有一个不为0,检验统计量如下
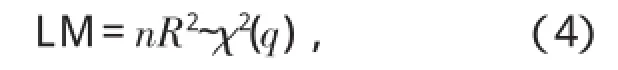

特别地,在LM检验中,(3)式的q值很大(一般q>7)时,检验依然显著,此时存在高阶ARCH效应,则考虑GARCH(p,q)。
1.3 ARCH参数估计
对ARCH模型中的参数进行估计时,采用极大似然方法进行估计。根据(2),(3)式建立回归-ARCH模型的对数似然函数为其中样本量为n,使得(5)式达到最大值时的α,β就是所求估计值。
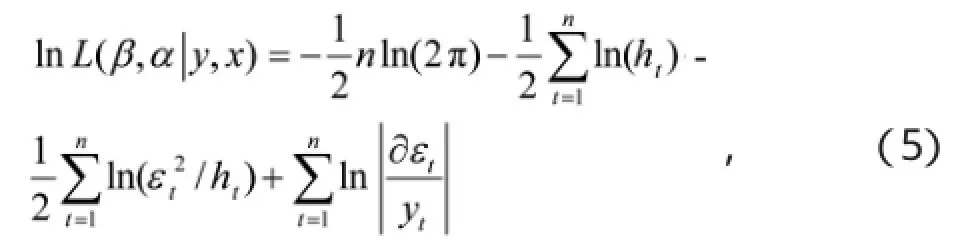
2 实证分析
2.1 数据处理及模型建立
本文数据来源于国家统计局(http://www.stats. gov.cn),通过整理得到。样本数据时间从2001年1月至2016年2月,共182个月我国水力发电量的数据,图1是我国水力发电量时间序列图。
从图1看出,该序列具有明显的季节性,对此通过乘积季节模型[7]进行调整,阶数为12的月度因子系数,如表1所示,消除季节趋势后发现残差序列无法通过白噪声检验。

图1 水力发电量时序图

表1 季节模型的因子指数
消除季节后的序列(图略)具有显著的递增趋势,初步判断序列具有自相关特征。若存在典型自相关,则对其序列构造异方差模型。首先,建立水力发电量y与时间t的回归模型,其结果如表2所示。
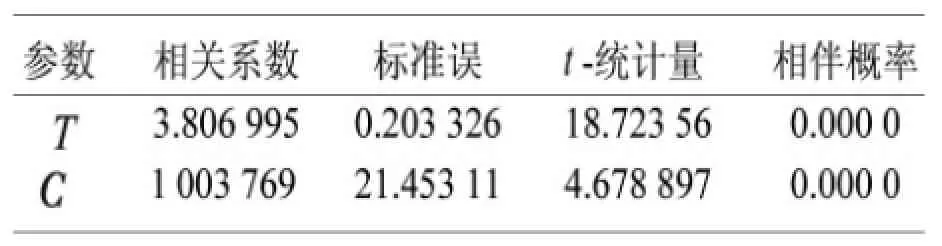
表2 y与时间t的回归模型
该回归模型的表达式为

表2的模型中T检验与F检验的相伴概率均小于显著水平0.05,通过模型的检验,但是模型的拟合优度R2=0.660 743,说明(6)式对数据的拟合程度不高,平均绝对误差MAPE=28.1000091,数值较大,且模型的杜宾检验DW=0.316 645,小于显著水平下的值,具有明显的自相关性,从而需要重新建立更加合适的模型进行预测。因此,对其残差做12阶自相关图,如图2所示,以及p=2阶序列自相关LM检验,如表3所示。

图2 我国水电量残差12阶差分自相关图

表3 LM检验
由图2、表3可知,自相关检验的Q统计量、自相关LM检验的相伴概率均小于0.05,故更加说明序列的残差存在高度自相关性,不满足白噪声。下面对其方差是否同质进行检验,对此选择残差序列的异方差性检验,结果如表4所示。

表4 异方差检验
由于Obs*R-squared统计量的相伴概率p<0.05,拒绝同方差的假设检验,故认为序列存在异方差性。故尝试构造ARCH模型,下面进行ARCH检验及LM检验,如表5所示。
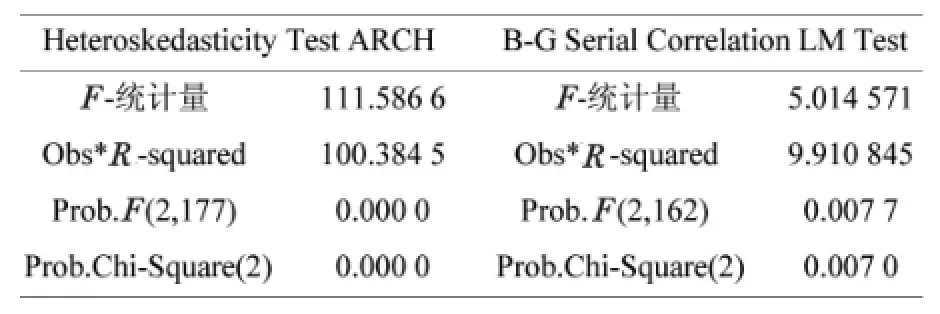
表5 ARCH检验及LM检验
由表5可知,χ2检验的相伴概率p=0.007 0,远小于显著水平α=0.05,则可以认为拒绝(3)各项系数都相等的原假设,即残差序列存在ARCH效应,即
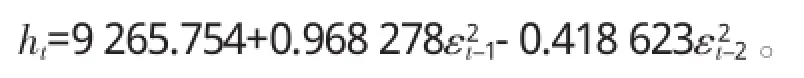
由于残差序列具有明显的ARCH效应,需要对残差序列ht进行自回归AR(p)模型拟合,对此采用逐步回归法[8]进行分析,结果如表6所示。

表6 残差序列逐步回归模型
由表6可以看出,该自回归AR(p)模型中仅有p=1,4,7,11阶时,参数的相伴概率均小于0.05,比较显著,通过模型的检验,由于AR(p)模型中的p>7,这表明模型服从高阶的ARCH(q)模型,对此应建立回归-GARCH(p,q)模型。选用GARCH(0,1)模型,通过最小二乘法及GARCH(0,1)混合模型拟合得出,GARCH(0,1)模型中的常数项与参数都通过检验,如表7所示。
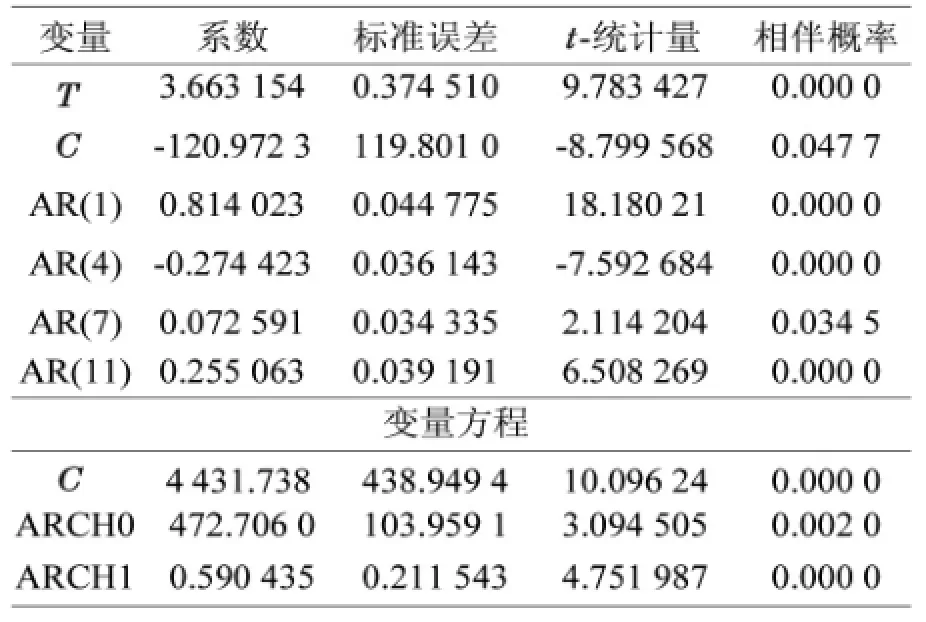
表7 回归-GARCH模型结果
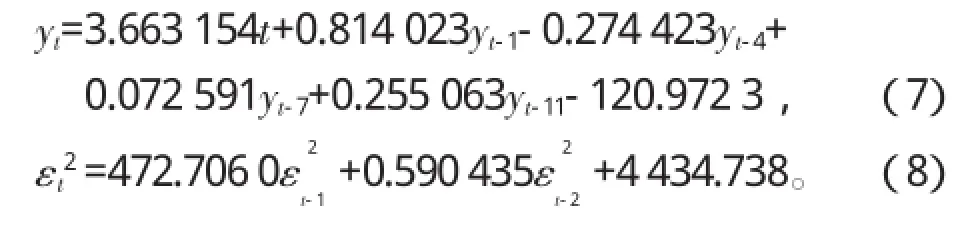
该模型的拟合优度为0.957677,非常接近于1,模型拟合非常好,杜宾检验DW=1.938 338,残差序列不存在自相关性,似然对数比值为-893.4728,AIC与SC值都比较小,可以认为该模型较好地拟合了数据。
2.2 模型有效性检验

图3 残差独立性检验
下面对混合模型的残差ηt进行独立性检验,如图3,可知:残差ηt的Q统计量的相伴概率均大于0.05,残差序列满足独立性;进一步,对残差ηt的正态性进行检验,且在这个检验中,正态性检验的χ2统计量的相伴概率p(value)=0.466 41>0.05,即残差序列通过了正态性检验,说明该模型AR(1,4,7,11)-GARCH(0,1)对数据的拟合十分合理。
最后,给出模型拟合后的效果,如图4,其中黑点为观察值序列,曲线为拟合值序列。拟合图形显示点线重合的比较好,这说明AR(1,4,7,11)-GARCH(0,1)模型拟合效果比较好,平均绝对误差MAPE=7.041 532 73,更加说明模型的合理性。
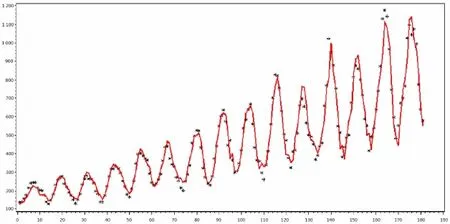
图4 模型拟合后的效果图
3 结论与建议
对于我国的水力发电量的研究用以往的普通回归模拟的方法拟合效果很差,拟合优度检验仅仅为0.660 743,杜宾检验DW=0.316 645,说明序列直接存在明显的自相关,自回归模型的拟合程度很差,一般是由序列的异方差性导致的。而利用回归-GARCH模型对水利发电量的预测进行建模,拟合优度检验提升为0.957 677,杜宾检验DW=1.938 338,说明序列不存在自相关性,建模通过了各项检验,取得了满意的效果,进而可以通过该模型对我国水电发电量进行合理的预测,能够对我国水电发电量的决策提供参考。
[1]康信茂.我国水力发电的现状及发展趋势[J].轻工科技,2016(3):64-65.
[2]ENGLERF.Autoregressive conditionalheteroscedasticitywith estimatesof thevarianceofUnited Kingdom inflation[J].Econometrica, 1982,50(4):987-1007.
[3]刘西陲,沈炯,李益国.基于加权双高斯分布的广义自回归条件异方差边际电价预测模型[J].电网技术,2010,34(1):139-144.
[4]刘达,王尔康,牛东晓.小波分析和考虑外生变量的广义自回归条件异方差模型在电价预测中的应用[J].电网技术,2009,33(18):99-104.
[5]吴其明,季忠贤,杨晓荣.自回归条件异方差(ARCH)模型及应用[J].预测,1998(4):47-54.
[6]黄春萍,倪宗瓒.自回归条件异方差模型在医学数据分析中的应用[J].数理医药学杂志,2004,17(4):341-343.
[7]徐国祥.统计预测与决策[M].5版.上海:上海财经大学出版社, 2016:51-55.
[8]易丹辉.统计预测:方法与应用[M].北京:中国人民大学出版社, 2014:44-46.
Hydropower Generating Capacity Forecasting Based on Auto-Regressive Conditional Heteroskedasticity Model
LUWei-xue,YANG Shi-juan,BAO Zhi-hui
(College ofMathmatic and Statistics,Huangshan University,Huangshan,Anhui245041,China)
The regularity of conditional variance variation and the statistical distribution characteristic of residual error of hydropower generating capacity(hgc)in hydropowermarket are researched.On this basis,bymeans of leading in the generalized auto-regressive conditional heteroskedasticity(GARCH)model,a GARCHmodel based on the Normal distribution is proposed to research the variation regularity of HGC.Taking the actual data from HGCmarket in China as samples,both GARCH model and the proposed GARCH model are tested.The testing results show that the GARCH model can offer good estimation and forecasting resultsof HGC.
auto-regressive conditional heteroskedasticity;GARCH model;hydropower generating capacity(hgc);normal distribution
F222;C812
A
1007-4260(2016)04-0019-04
时间:2017-1-3 17:19
http://www.cnki.net/kcms/detail/34.1150.N.20170103.1719.006.html
2016-04-02
黄山学院自然科学研究项目(2015xkj004,2015xkj005)和安徽省教育厅科研项目(KJHS2016B04,KJ2011Z364)。
卢维学,男,黑龙江依安人,硕士,黄山学院数学与统计学院教师,研究方向为数理统计。E-mail:lwx@hsu.edu.cn
10.13757/j.cnki.cn34-1150/n.2016.04.006
