鼓泡塔中气泡群运动的实验与模拟

周晓琳，田 震，王丽军，成有为，李 希

浙江大学化学工程与生物工程学院，浙江 杭州 310027

鼓泡塔中气泡群运动的实验与模拟

周晓琳，田 震，王丽军，成有为，李 希

浙江大学化学工程与生物工程学院，浙江 杭州 310027

采用高速摄像法测量了均匀鼓泡流状态下，水以及体积分数分别为20%和40%的甘油-水体系中气泡群的浮升运动，考察了气含率、雷诺数和分布器孔径对气泡尺寸、形状、浮升速率和曳力系数的影响。构建了立方体单元胞模型，并根据雷诺数的不同选取层流和湍流模型，模拟得到气泡的浮升速率和曳力系数与实验值吻合较好。结果表明：随着气含率及液体黏度的提高，气泡群浮升阻力增大，浮升速率减少；随着雷诺数和气泡直径的增加，曳力系数减小，气泡浮升速率增大。单元胞模型能较好地反映气泡群浮升过程中各因素的影响，是处理气泡群运动的有效工具。

气泡群 高速摄像 单元胞模型 曳力系数

鼓泡塔具有结构简单、操作方便、无机械传动部件及相间接触面积大等优点，被广泛地应用于化工生产过程。鼓泡塔中气泡群的浮升及其与液体间的相互作用决定了鼓泡塔的流动特性，有关鼓泡塔内气泡群的研究较多。Martinez-Mercado等[1,2]使用双电导探针法研究了气泡群浮升过程中气泡直径和相对滑移速率等参数。Rabha等[3]采用高速摄像技术研究了气泡群在均匀分布和非均匀分布条件下的气泡直径和浮升速率随气含率的变化，高速摄像所获得的图像更直观，可靠性较高，更适用于气速较低的均匀鼓泡的情况。在气泡群运动模拟方面，目前采用的模型主要为直接数值模拟（DNS）和单元胞模型。DNS能更好地描述气泡群的真实运动，但模型的计算量较大。Bunner等[4]用DNS模拟了216个气泡，计算耗时数十天。单元胞模型由Happel[5]提出，该模型的核心是将液体均分，通过计算典型单个气泡，获得气泡群浮升运动规律。相对DNS模型，单元胞模型的计算量较小。Leclair等[6]用单元胞模型模拟了雷诺数（Re）小于1 000时的球形气泡群，模拟与实验值吻合较好。Manjunath等[7]用单元胞模型研究了Re小于100时气泡群曳力系数与气含率和雷诺数的关系。毛在砂[8]模拟了Re为50时气泡的运动，并考虑了气泡在运动过程中的变形。本工作使用高速摄像方法拍摄3种不同黏度状态下液体中气泡群浮升过程，测量了气泡大小、形态变化以及浮升速率等，并利用单元胞模型进行气泡群浮升速率和曳力计算，通过选取合适的单元胞结构和流体方程，将单元胞模型应用于更宽的雷诺数范围。从实验和理论两方面对鼓泡塔中气泡群浮升运动规律进行研究。

1 实验部分

1.1 实验装置

实验装置如图1所示，主要包括流体控制和检测两个部分。流体控制系统由空气压缩机、储蓄罐、调压器、测试塔和阀门等组成。鼓泡塔为长方体透明有机玻璃水槽，尺寸为170 cm×15 cm×5 cm，厚度方向比较小，近似可作为二维鼓泡塔，塔底部采用分布器进气，进气口均匀分布于塔底，为考察进气孔径的影响，选择了0.2和0.6 mm两种孔径分布器。测量系统由压差计和图像采集装置组成。压差计用于测量塔内平均气含率。图像装置设备包括照明、高速摄像机和计算机等单元。采用德国Mikrotron公司的Cube7高速摄像机测量二维鼓泡塔中的气泡群浮升运动，每秒1 000幅的拍摄速度，采用1 000 W的冷光源逆向照射，拍摄垂直方向气泡的运动图像，采集图像分辨率为1 024×1 024，帧频为500 fps。

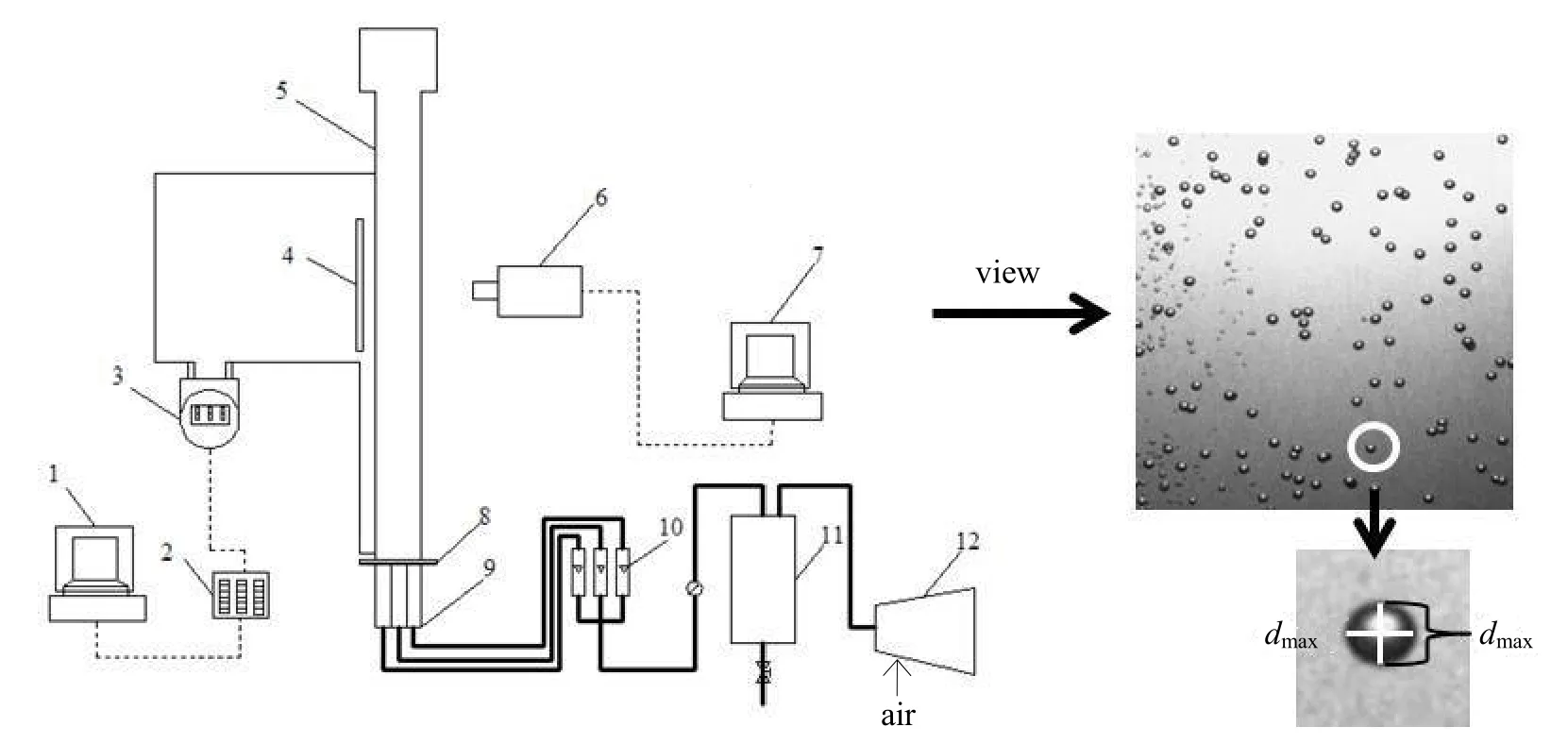
图1 实验装置及典型气泡示意Fig.1 Experimental set-up and typical bubble figure1,7-computer; 2-A/D conversion card; 3-pressure transmitter; 4-light; 5-bubble column; 6-camera; 8-gas distributor; 9-gas chamber; 10-flow meter; 11-gas buffer tank; 12-compressor

实验所用气体为空气，为考察雷诺数变化对气泡浮升运动的影响，选择了水及两种配比的水-甘油混合物（室温10.3 ℃）为液相流体，相关组成及物性列于表1。在此3种气液体系下，当气体的表观气速小于0.05 m/s，鼓泡流型为均匀鼓泡流，气泡群浮升过程中不存在气泡聚并和破碎现象。

表1 液相组成及物理性质Table 1 Liquid phase composition and physical properties

1.2 实验步骤

首先进行尺寸标记，向鼓泡塔中注入液体，并放入6 mm管，调节高速摄像机焦距以获得最清晰的图像，作为测量气泡尺寸的基准；然后打开空气压缩机，调节流量计，使空气通过分布器以鼓泡形式均匀进入鼓泡塔中；待鼓泡塔运行稳定后，进行图像实时采集，不断调节流量计改变表观气速，获得不同表观气速实验数据。为考察分布器孔径影响，更换不同孔径分布器孔，再次重复以上实验步骤。

1.3 图像处理

图像分析采用Matlab编程实现，将采集的图像转化为灰度图，如图2所示。气泡所对应的灰度较高，因而可利用图像中灰度的梯度变化识别每一个气泡的边缘信息，并通过全局阈值设置调节图像的分辨率。为计算气泡的尺寸，使用标准6 mm的实心管在测量位置上进行标定，通过拍摄到的气泡大小与标定管的尺寸比较，确定变形椭球气泡长轴dmax，短轴dmin和纵横比x（x=dmax/dmin），得到气泡的等效直径。气泡浮升速率采用颗粒跟踪算法（PTV）计算，根据所获得的动态图像，在较短的时间间隔内，跟踪每个气泡的运动轨迹，计算出单个气泡浮升速率的瞬时速率，进而得到平均浮升速率（Vg），根据式（1）计算气泡的曳力系数（CD）：

式中：Vrel=Vg-Vl，在本实验所考虑的均匀鼓泡流范围内，Vl≈0，Vrel≈Vg。

2 单元胞数学模型

单元胞模型是处理鼓泡塔内气泡群浮升运动的重要方法，其假设气泡群中的气泡均匀地分布在液体中，并且每个气泡表面携带的液体量相等，单元胞由位于中心的气泡和它周围的液体所构成，单元胞中气液间的体积比例与鼓泡塔的平均气含率一致。

2.1 单元胞模型

Happel等[5-7]采用球形单元胞，球形的对称性好且理论推导方便。Sirignano等[9]认为更合理的单元胞形状是立方体形，不足之处是立方体单元胞属于三维问题，求解计算量较大，但随着计算机能力的提高，求解3维计算流体力学（CFD）问题目前已不困难，因而本工作采用立方体单元胞模型模拟气泡群运动。

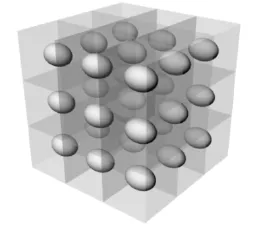
图2 单元胞模型示意Fig.2 Diagram of cell model

图3 单气泡绕流示意Fig.3 Diagram of flow around the single bubble

立方体单元胞如图2所示，假设气泡以相同的间隔均匀地分布在液体里，每个气泡分属于各自的立方体内，研究一个立方体中的流场即可掌握整个气泡群的运动规律。以气泡作为运动参考系，图3给出了立方体单元胞中的绕流场的速度分布。

2.2 流体力学方程

有关单元胞流体力学模型均采用层流方程，适用雷诺数较低的情况[7,8,10]，本实验在水体系下，气泡的浮升雷诺数接近1 000，应该使用湍流模型进行模拟，而对于水-甘油混合体系，液体黏度较高，雷诺数为50～400，可以采用Navier-Stokes方程计算，相关流体力学方程列于表2。

表2 流体力学方程Table 2 Fluid mechanics equations

单元胞中心气泡为椭球形，椭球长轴和短轴大小通过实验拍照确定。椭球所占立方体单元胞体积分数等于全塔气含率，故立方体单元胞边长（a）为：

边界条件为：（1）单元胞之间的分界壁为对称边界条件，二维鼓泡塔中单元胞与容器壁面边界条件采用无滑移边界条件，湍流模型使用标准壁函数；（2）气泡表面采用部分滑移边界条件，参照文献[10]，设置污染角为90°；（3）入口和出口定义为充分发展边界，以保证进出口流体分布规律相同，给定入口及出口边界的质量流率。

2.3 求解方法

模型采用Star-CCM+10.0软件求解，采用三维稳态模拟，使用分离求解器，收敛标准为相对残差小于10-3。利用几何结构的对称性，仅选取一半的物理区域进行计算，以减少计算负荷。使用Star CCM+特色的网格划分工具划分多面体网格，所需内存较少，求解速率较快。网格密度设置为：当αg小于2%时，网格基本尺寸为3×10-4m；当αg大于2%时，网格基本尺寸为1.5×10-4m，该网格密度通过网格无关性检验。

3 结果与讨论

3.1 平均气含率

图4 不同表观气速下全塔气含率Fig.4 Gas holdup of whole tower as a function of superficial gas velocity

全塔平均气含率随表观气速的变化如图4所示。由图可知，随着表观气速的增大，平均气含率单调递增，且3种液体中气含率随表观气速变化规律相近。在本实验范围内，气含率与表观气速满足线性关系。

3.2 气泡尺寸和形状

在相同表观气速下3种不同体系中拍摄得到的典型气泡群浮升图像如图5所示。图5（a）～（c）采用的分布器孔口直径为0.2 mm，图5（d）～（f）使用的分布器孔口直径为0.6 mm。由图可知，气泡为椭球形，水体系中气泡等效直径大于水-甘油混合体系，并且随着气含率的增大气泡变形程度增大。在0.6 mm分布器条件下，水体系中气泡变形高于水-甘油混合体系。

图5 典型气泡群运动Fig.5 Motion diagram of typical bubble swarma, d-water; b, e-20% glycerol-water; c, f-40% glycerol-water

图6为在不同气含率下3个体系中的气泡等效直径。由图可知，随着气含率的增大，气泡等效直径增大，纯水中气泡直径明显大于水-甘油混合体系。这是由于降低液体表面张力可以减小气泡尺寸，而水的表面张力最大。对比0.2和0.6 mm孔径分布器，大孔径分布器所得到的气泡直径也较大，说明在均匀鼓泡状态下，气泡尺寸受分布器影响较大。

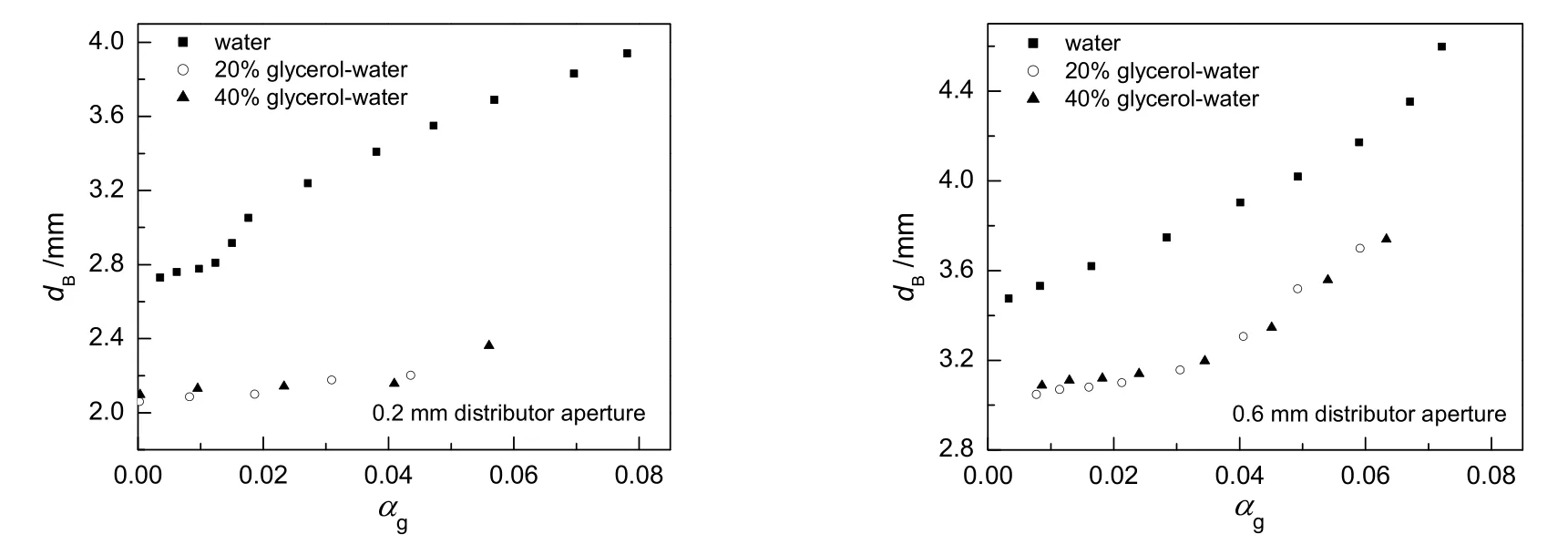
图6 不同气含率下气泡等效直径Fig.6 Equivalent diameter of bubble as a function of gas holdup

3.3 气泡浮升速率

图7为实验和模拟得到的气泡浮升速率。由图可以看出，气泡浮升速率均随着气含率增大而减小，这是由于气泡群随着气含率的增大，气泡间距减少，气泡浮升过程中气泡间隙处的气液相对滑移速率增大，使得气泡所受阻力增大，导致气泡浮升速率减小。由图还可以看到，随着甘油浓度的增加，气泡浮升速率减少，这是由于甘油含量的增大使得液体黏度增大，摩擦阻力增大。对比不同分布器孔径结果，分布器孔径增加，气泡浮升速率增大，这是由于大孔分布器产生的气泡等效直径大，所受浮力更大。

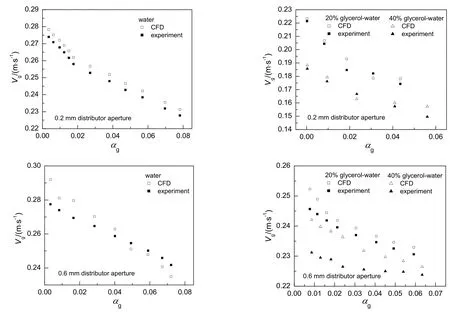
图7 不同气含率下气泡浮升速率Fig.7 Bubble velocity as a function of gas holdup

对比模拟与实验结果可知，在0.2 mm分布器条件下，模拟和实验吻合结果更好，0.6 mm分布器条件下偏差增大，这可能是因为大孔径分布器产生的气泡在浮升过程中动态变形较大，单元胞模型很难描述这种现象。此外，随着体系黏度增加，模拟与实验值间误差也增大，实验发现黏度提高，气泡团聚有所增加，导致实验值与模拟值的偏差。

3.4 气泡曳力系数

表3为实验和模拟得到的曳力系数相关数据汇总，气泡的曳力系数实验值和模拟值的相对误差在±10%左右，二者符合较好，说明单元胞模型能较好地描述均匀鼓泡流中气泡群所受到的阻力。由表可知，随着气含率的增大气泡的变形程度增大，浮升速率减小，曳力系数增加。

使用立方体单元胞模型计算得到雷诺数对气泡曳力系数的影响结果见图8。由图可知，随着雷诺数的增加，气泡曳力系数减小，在低气含率层流条件下，模型计算结果与Tomiyama等[11]给出的单气泡曳力公式符合较好。在高雷诺数情况下，湍流模型与层流模型计算结果差异较大，在水体系中湍流模型与实验结果吻合较好，说明高雷诺数下，采用湍流模型更合理。

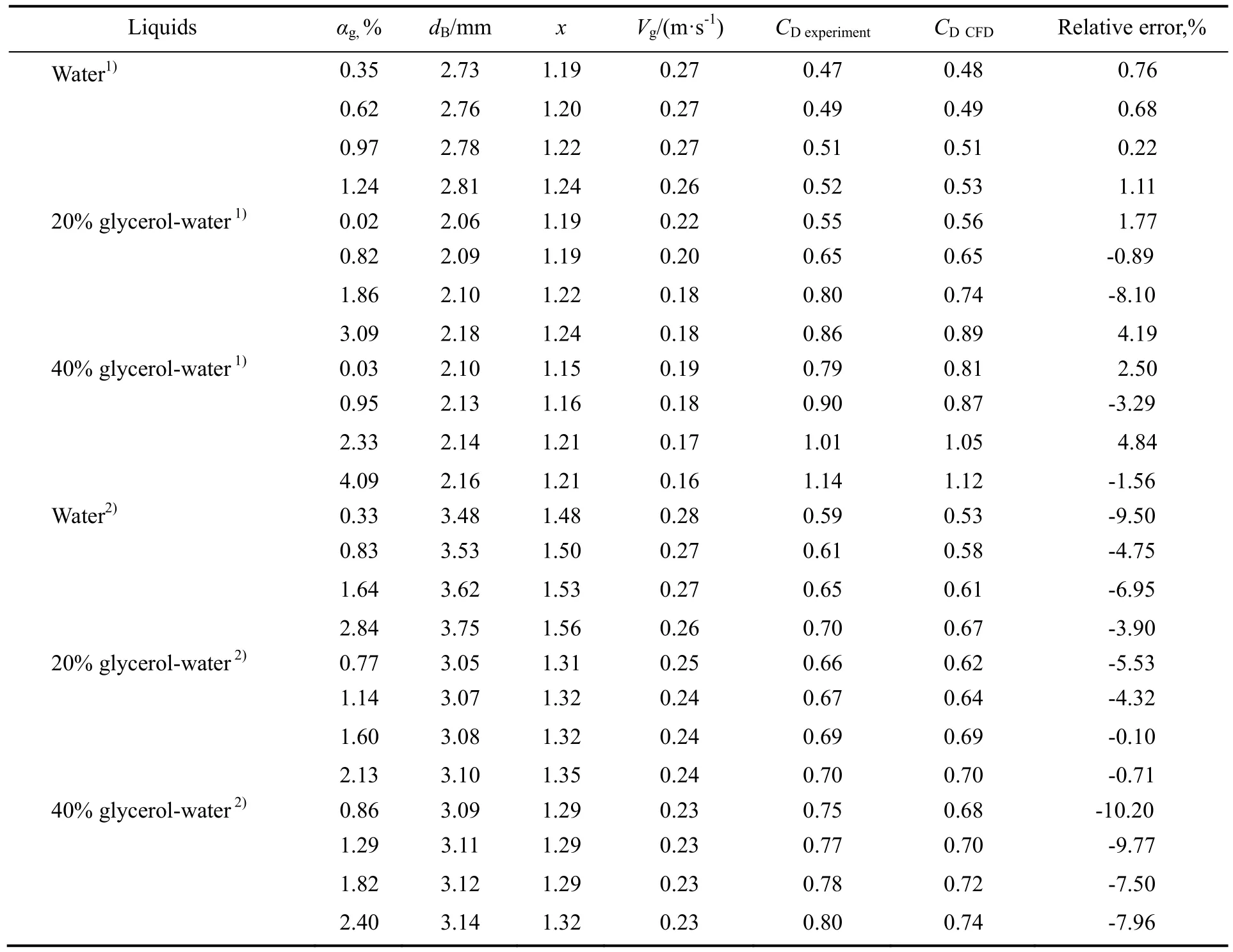
表3 曳力系数相关数据汇总Table 3 Summary of drag coefficient data

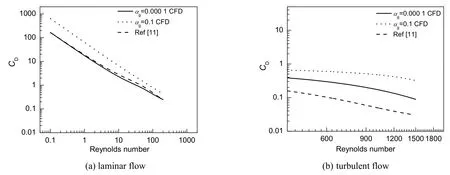
图8 不同雷诺数下曳力系数值Fig.8 Drag coefficient as a function of Reynolds number

Manjunath等[7,8]采用单元胞模型研究了Re为50时，气泡曳力系数与气含率的关系，相同条件下采用本实验模型进行了模拟计算，结果见图9（a）。由图可知，随着气含率的增大，气泡曳力系数增大，文献[7]的结果明显偏小。这主要是由于其没有考虑气泡变形，本实验模型计算结果与文献[8]的结果略有偏差，可能是由于本实验采用立方体单元胞，而文献[8]采用球形单元胞。图9（b）进一步给出了在较高雷诺数情况下，预测气泡曳力系数与气含率的关系，随着气含率的增大，气泡曳力系数随之增大。

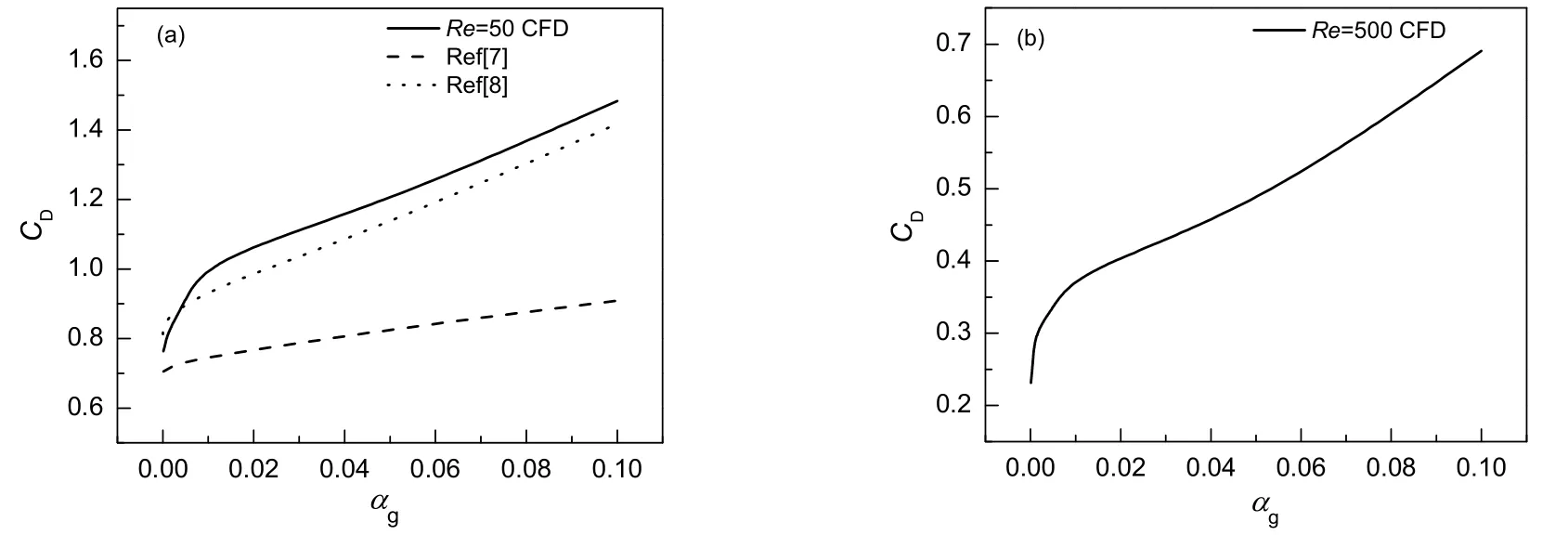
图9 不同气含率下曳力系数值Fig.9 Drag coefficient as a function of gas holdup

4 结 论

采用高速摄像法测量了水、20%甘油-水和40%甘油-水3种体系中均匀鼓泡流状态下的气泡群浮升运动，构建了立方体结构的单元胞数学模型，实验及模拟结果表明：

a）随着气含率的增大，气泡等效直径增加，气泡变形程度增大，气泡间隙处的流体运动受到阻碍，气泡的曳力系数增大，浮升速率减小。

b）随着液体黏度增大，气泡等效直径减小，并且0变形程度较小，黏度的增大使气泡所受摩擦阻力增大，气泡浮升速率减小，曳力系数增大。

c）气泡尺寸与分布器孔径有关，分布器孔径对气泡浮升速率有较大影响。

d）随着雷诺数的增加，气泡的曳力系数减小，水体系中采用湍流模型更合理。

e）计算得到的气泡浮升速率及曳力系数与实验值符合较好，本工作所提出的单元胞模型能较好地预估均匀鼓泡流中气泡群浮升的运动行为。

符号说明

参考文献：

[1] Martínez-Mercado J, Palacios-Morales C A, Zenit R. Measurement of pseudoturbulence intensity in monodispersed bubbly liquids for 10＜Re＜ 500[J]. Physics of Fluids, 2007, 19(10): 103302.

[2] Simonnet M, Gentric C, Olmos E, et al. Experimental determination of the drag coefficient in a swarm of bubbles[J]. Chemical Engineering Science, 2007, 62(3): 858-866.

[3] Rabha S S, Buwa V V. Experimental investigations of rise behavior of monodispersed/polydispersed bubbly flows in quiescent liquids[J]. Industrial & Engineering Chemistry Research, 2010, 49(21): 10615-10626.

[4] Bunner B, Tryggvason G. Dynamics of homogeneous bubbly flows part 1: rise velocity and microstructure of the bubbles[J]. Journal of Fluid Mechanics, 2002, 466(1): 17-52.

[5] Happel J. Viscous flow in multiparticle systems: slow motion of fluids relative to beds of spherical particles[J]. AIChE Journal, 1958, 4(2): 197-201.

[6] Leclair B P, Hamielec A E. Viscous flow through particle assemblages at intermediate Reynolds numbers: a cell model for transport in bubble swarms[J]. The Canadian Journal of Chemical Engineering, 1971, 49(6): 713-720.

[7] Manjunath M, Tripathi A, Chhabra R P, et al. Numerical simulation of the drag on a swarm of bubbles[J]. International Journal of Engineering Science, 1994, 32(6): 927-933.

[8] 毛在砂. 用单元胞模型数值模拟气泡群中气泡的运动[J]. 化工学报, 2007, 58(5): 1155-1162. Mao Zaisha. Cell model approach to motion of bubbles in swarm[J]. Journal of Chemical Industry and Engineering, 2007, 58(5): 1155-1162.

[9] Sirignano W A, Tal R. Cylindrical cell model for the hydrodynamics of particle assemblages at intermediate Reynolds numbers[J]. AIChE Journal, 1982, 28(2): 233-237.

[10] Nalajala V S, Kishore N, Chhabra R P. Effect of contamination on rise velocity of bubble swarms at moderate Reynolds numbers[J]. Chemical Engineering Research and Design, 2014, 92(6): 1016-1026.

[11] Tomiyama A, Kataoka I, Zun I, et al. Drag coefficients of single bubbles under normal and micro gravity conditions[J]. JSME International Journal Series B: Fluids and Thermal Engineering, 1998, 41(2): 472-479.

Experiment and Numerical Simulation of the Motion of Bubble Swarm in a Bubble Column

Zhou Xiaolin, Tian Zhen, Wang Lijun, Cheng Youwei, Li Xi
Department of Chemical and Biological Engineering, Zhejiang University, Hangzhou 310027, China

High-speed digital video processing was used to measure the motion of bubble swarm in water, 20% glycerol-water and 40% glycerol-water mixture under the uniform bubble flow state, respectively. The effects of gas holdup, Reynolds number and distributor aperture on the bubble size and shape, bubble velocity and drag coefficient were investigated. The cubic cell model was established and the laminar flow model and turbulent flow model were selected according to the different Reynolds number to simulate the motion of the bubble swarm. The results showed that the numerical rise velocity and the drag coefficient of the bubbles were in good agreement with the experimental data. The rise resistance of the bubble swarm increased and the rise velocity decreased with the increase of gas holdup and liquid viscosity. With the increase of the Reynolds number and the bubble equivalent diameter, the bubble swarm drag coefficient decreased and the rise velocity increased. It is suggested that the cell model can well reflect the influences of various factors in the process of the bubble swarm motion and it is an effective tool to deal with the movement of the bubble swarm.

bubble swarm; high-speed video; cell model; drag coefficient

TQ018；TQ021.1

：A

1001—7631 ( 2016 ) 06—0481—09

2016-03-21；

：2016-09-27。

周晓琳（1991—），女，硕士研究生；王丽军（1976—），男，博士，副研究员，通讯联系人。E-mail: wang_lijun@zju.edu.cn。

国家自然科学基金重大研究计划（91334105）。