非高斯噪声激励下双稳系统的平均首次穿越时间

赵 燕

(山西省机电职业技术学院 基础部，山西 长治 046001)

非高斯噪声激励下双稳系统的平均首次穿越时间

赵 燕

(山西省机电职业技术学院 基础部，山西 长治 046001)

研究了非高斯噪声激励下的双稳系统，应用路径积分和统一色噪声近似的方法得到系统的定态概率密度和平均首次穿越时间的表达式.发现了噪声强度、偏离参数及自相关时间均不能诱导非平衡相变发生；非高斯噪声强度D和加性噪声强度Q的增加有利于粒子的逃逸；自相关时间τ0的增加会阻碍粒子的逃逸；当非高斯噪声强度D较小时，非高斯噪声参数p值增大会阻碍粒子的逃逸，当D增加到一定值时，p值的增大就会利于粒子的逃逸.

双稳系统；非高斯噪声；定态概率密度；平均首次穿越时间

噪声根据统计性质通常分为高斯噪声和非高斯噪声两类.一般高斯噪声便于运算处理，而非高斯噪声[1]属于非马尔科夫过程不容易处理，所以研究非高斯噪声的文章较少.近20年，人们对双稳系统的研究有很多，靳艳飞等[2]研究了色关联的色噪声驱动的双稳杜芬模型的稳态分析，罗晓勤等[3]讨论了由两种不同色噪声驱动的双稳系统的随机共振现象.非高斯噪声驱动的双稳系统的研究是一篇基础性的研究.

本文主要研究了非高斯噪声激励下双稳系统的定态概率密度和平均首次穿越时间，应用路径积分法将非高斯噪声处理成高斯色噪声，根据统一色噪声理论近似得到系统的FPK方程和定态概率密度函数.用平均首次穿越时间的定义得到粒子在两个稳态之间的跃迁时间的表达式，讨论了非高斯加性噪声强度Q，乘性噪声强度D、偏离参数p及关联时间τ0对定态概率密度和平均首次穿越时间的影响.

1 双稳系统的稳态定态概率密度函数

由乘性非高斯噪声和加性白噪声激励下的双稳杜芬系统模型，其遵循的朗之万方程为：

(1)

(2)

其中U(x)是杜芬的双稳势阱，有两个稳定点x1=-1，x2=1和一个不稳定点x0=0,η(t)是非高斯噪声，具有下列分布：

(3)

式中p表示非高斯噪声η(t)偏离高斯分布的程度，显然p≠1(若p=1，则η(t)不再是非高斯噪声，成为自相关时间为τ0，噪声强度为D的高斯色噪声)；ε(t)和ξ(t)都是具有零均值的相关白噪声，其统计性质如下：

〈ε(t)〉=0，〈ε(t)ε(t′)〉=2Dδ(t-t′)

〈ξ(t)〉=0，〈ξ(t)ξ(t′)〉=2Qδ(t-t′)

〈ε(t)ξ(t′)〉=〈ξ(t)ε(t′)〉=0

(4)

其中，D和Q分别是高斯白噪声ε(t)和ξ(t)的噪声强度.非高斯噪声η(t)的统计性质如下：

〈η(t)〉=0

(5)

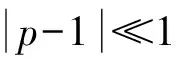
(6)

这里ε1(t)为高斯白噪声，

〈ε1(t)〉=0，

〈ε1(t)ε1(t′)〉=2D1δ(t-t′)，

〈ε1(t)ξ(t′)〉=〈ξ(t)ε1(t′)〉=0

(7)

这里的τ1和D1为有效噪声的相关时间和有效噪声强度

(8)

此时，非高斯噪声η(t)近似为关联时间为τ1，噪声强度为D1的高斯色噪声.再利用统一色噪声近似[5]求解出方程(1)的近似FPK方程表达式：

(9)

其中，

(10)

根据方程(9)和方程(10)得近似的稳态概率密度函数为:

(11)

(12)

经过计算得：

(13)

图1 定态概率密度函数pst(x)在不同乘性噪声强度D的变化曲线Q=0.5,p=0.5，τ0=0.3

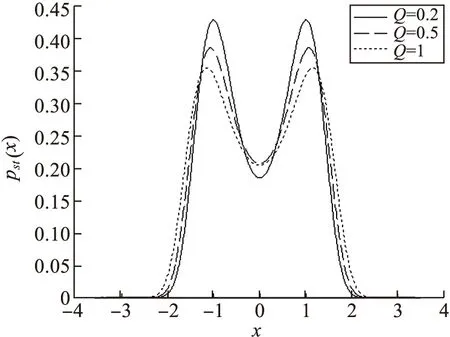
图2 定态概率密度函数pst(x)在不同加性噪声强度Q的变化曲线D=0.5,p=0.5，τ0=0.3

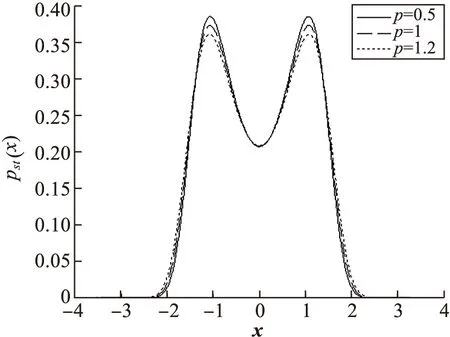
图3 定态概率密度函数pst(x)在不同非高斯参数p的变化曲线D=0.5，Q=0.5，τ0=0.3

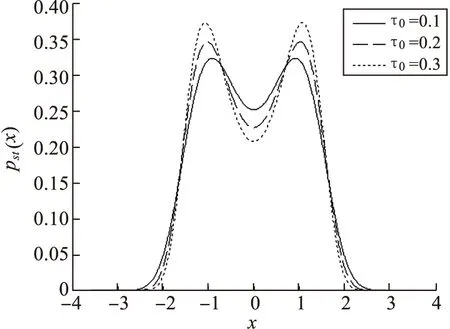
图4 定态概率密度函数pst(x)在不同自相关时间τ0的变化曲线D=0.5，Q=0.5，p=0.5

图1～4中，我们观察到非高斯噪声的噪声强度D，非高斯参数p，自相关时间τ0和加性噪声强度Q变化时，稳态概率密度函数pst(x)的双峰始终对称出现在x=±1附近，pst(x)的谷底始终在x0=0处.当非高斯噪声的噪声强度D值从0增加到0.25时，pst(x)的峰值先快速变大，但随着D值得继续增加，峰值出现下降；同时随着D值得增加，谷值单调升高.随着加性噪声强度Q值的增加，pst(x)的峰值逐渐降低，谷值先升高后有略微的降低.随着非高斯参数p值的增加，pst(x)的峰值逐渐降低，谷值基本变化不大.自相关时间τ0和加性噪声Q对稳态概率的影响相反，随着τ0值的增加，pst(x)的峰值逐渐上升，谷值逐渐下降.综上4图可以发现pst(x)图形始终是对称的双峰结构.因此，乘性非高斯噪声强度D和加性噪声强度Q、偏离参数p及自相关时间τ0均不能诱导非平衡相变发生.

2 非高斯噪声驱动的FHN模型的平均首次穿越时间

根据平均首次穿越时间的定义和最速下降法得到：粒子从一个稳态到另一个稳态的平均首次穿越时间为：

(14)

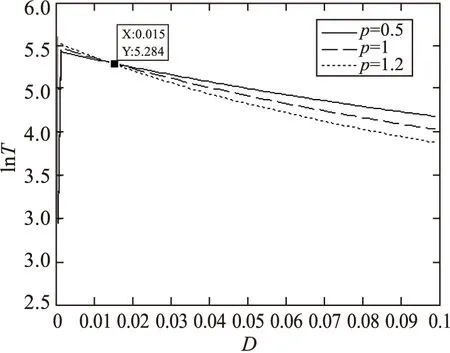
图5 T+作为乘性噪声强度D的函数随不同的偏离参数p变化的曲线Q=0.1，τ0=0.1

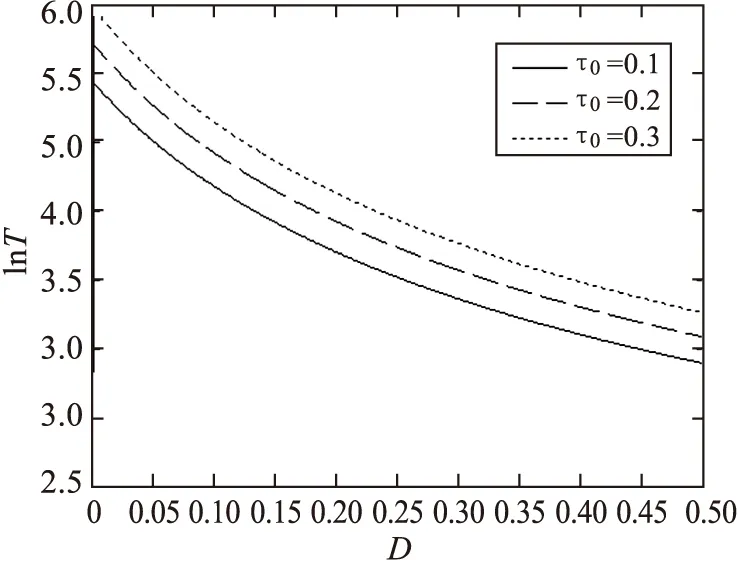
图6 T-作为乘性噪声强度D的函数随不同的自相关时间τ0变化的曲线Q=0.1，p=0.5

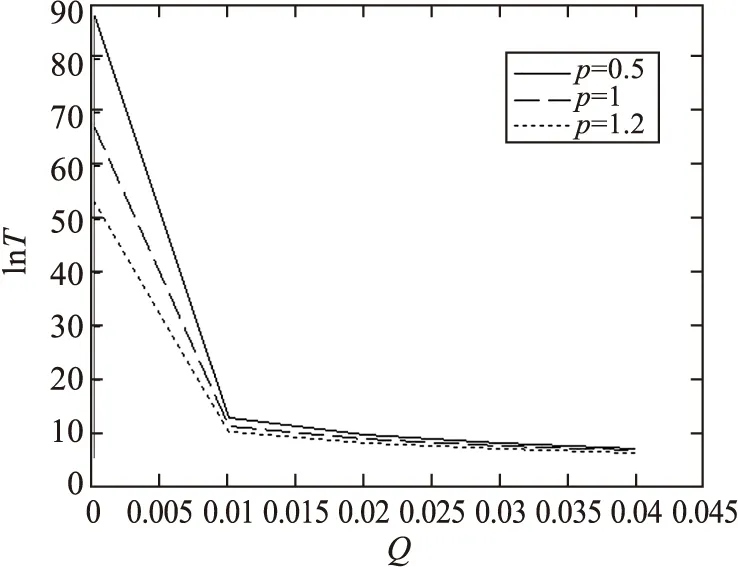
图7 T+作为加性噪声强度Q的函数随不同的偏离参数p变化的曲线D=0.1，τ0=0.1

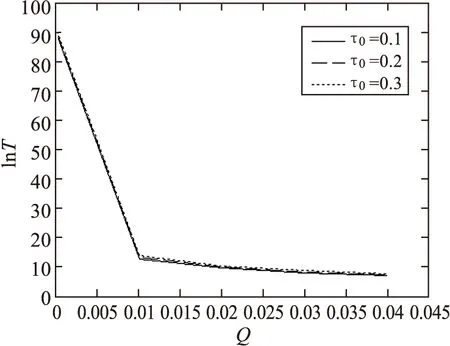
图8 T-作为加性噪声强度Q的函数随不同的自相关时间τ0变化的曲线D=0.1，p=0.5

从图5～8可以看到平均首通时间T随非高斯噪声的噪声强度D值和加性噪声强度Q值的增加而减少，说明乘性非高斯噪声强度D和加性噪声强度Q会加速粒子的跃迁.在图5中，平均首通时间T并不是随着非高斯噪声参数p值的增加而单调变化的，当非高斯噪声的噪声强度D<0.015时，平均首通时间T随p的增大而增大；当D≥0.015时，平均首通时间T随p的增大而减小，即当D<0.015时，非高斯噪声参数p的增大阻碍了粒子的跃迁，当D≥0.015时，p的增大利于粒子的跃迁.观察图6可知，固定D值，平均首通时间T随着自相关时间τ0的增加而增加.说明自相关时间的增大会阻碍粒子的跃迁.从图7看到，当加性噪声强度Q<0.01时,平均首通时间T随着Q值的增加骤降，当Q≥0.01时，均首通时间T在缓慢的几乎趋于平缓的下降.图8看到，固定Q值时，自相关时间τ0的增加几乎不会改变平均首通时间T.

3 结论

文中得到了由乘性非高斯噪声及加性白噪声共同驱动的双稳模型的定态概率密度和平均首次穿越时间的表达式.发现非高斯噪声和加性噪声均不能诱导非平衡相变的发生；非高斯噪声强度D值和加性噪声强度Q值的增加会减少粒子在两稳态之间的跃迁时间；当非高斯噪声强度D较小时，非高斯噪声参数p值增大会增加粒子在两个稳态间的跃迁时间，当D增加到一定值时，p值的增大会缩短粒子在两个稳态间的跃迁时间；当加性噪声强度Q较小时，非高斯噪声参数p对平均首通时间T的影响较大，即p值的增加会明显的降低粒子在两势阱之间的跃迁时间，当Q较大时，p对平均首通时间T的影响程度减小，即p值的增加仍然会降低粒子在两势阱之间的跃迁时间；非高斯噪声的自相关时间τ0的增加会延长粒子在两个稳态之间的跃迁时间.

[1]WIESENFELDK,PIERSOND,PANTAZELOUE,etal.Stochasticresonanceonacircle[J].Phys.Rev.Lett,1994,72:2125-2129.

[2] 靳艳飞，徐伟，李伟，等.色关联的色噪声驱动的双稳杜芬模型的稳态分析[J].动力学与控制学报，2005,3(2):62-67.

[3]LUOXQ,ZHUSQ.Stochasticresonancedrivenbytwodifferentkindofcolorednoiseinabistablesystem[J].Phys.Rev.E,2003,67:1104-1113.

[4]FUENTESMA,TORALR,WIOHS.Enhancementofstochasticresonance:Theroleofnon-Gaussiannoise[J].PhysicaA, 2001,295:114-122.

[5]CAOL,WUDJ,KESZ.Bistablekineticmodeldrivenbycorrelatednoises:Unifiedcolored-noiseapproximation[J].Phys.Rev.E,1995,52(3):3228-3231.

[责任编辑 王新奇]

The Mean First Passage Time for A Bi-stable System Drivenby Non-Gaussian Noise

ZHAO Yan

(Basic Department, Shanxi Institute of Mechanical & Electrical Engineering, Changzhi 046001, China)

In this paper, the bi-stable system driven by non-Gaussian noise is studied. The expressions of the stationary probability distribution and the mean first-passage time are obtained through the approach and the unified colored noise approximation. The results show that the path-integral intensity of noise, the derivation parameter and the self correlation time cannot induce phase transition. The increase of the non-Gaussian noise intensity and additive noise intensity enhance the escape, while increase of the self correlation time reduces the escape. When the D value of non-Gaussian noise intensity is small, the p value increase of non-Gaussian noise parameter can hinder the particle’s escape; when the D value of non-Gaussian noise intensity is added to a certain value, the increase of p value will be conducive to the particle’s escape.

bi-stable system; non-Gaussian noise; steady state probability distribution; mean first passage time

1008-5564(2016)05-0021-05

2016-03-19

赵 燕(1982—)，女，山西长治人，山西机电职业技术学院基础部讲师，理学硕士，主要从事非线性动力随机系统研究.

O324

A