融合IWT与SVD的鲁棒和隐蔽性数字图像水印方案*

廖洪建， 黄良永

(1.广西科技师范学院 数学与计算机科学学院，广西 来宾 546199) (2.武汉理工大学 信息工程学院，湖北 武汉 410082)



融合IWT与SVD的鲁棒和隐蔽性数字图像水印方案*

廖洪建1*， 黄良永1,2

(1.广西科技师范学院 数学与计算机科学学院，广西 来宾 546199) (2.武汉理工大学 信息工程学院，湖北 武汉 410082)

针对数字图像水印的鲁棒性和隐蔽性问题，提出一种基于整数小波变换(IWT)和奇异值分解(SVD)的图像水印方案.首先，利用整数小波变换将宿主图像变换到小波域.然后，在获得的每个频带上进行奇异值分解，并根据比例因子将水印嵌入奇异值中.最后，在权衡考虑鲁棒性和隐蔽性下，利用粒子群优化(PSO)算法获得最优的比例因子.实验结果表明，该水印方案对常见的图像处理操作具有较好的鲁棒性，同时保持了优良的隐蔽性.

图像水印；整数小波变换；奇异值分解；粒子群优化算法

随着图像安全技术的发展，数字水印技术在图像安全领域得到广泛应用.数字水印图像一般分为水印生成、水印嵌入和水印萃取三个部分.水印嵌入过程可以分为两类：空间域嵌入和变换域嵌入.其中，嵌入变换域的水印具有更好的鲁棒性[1].最常见的两种变换域方法是离散余弦变换(Discrete Cosine Transform, DCT)[2]和离散小波变换(Discrete Wavelet Transform, DWT)[3].在基于DWT的水印方法中，将宿主图像变换到小波域，然后将水印插入三个子频带中的有效系数上，即LL(低-低)、LH(低-高) 和HL(高-低).鲁棒性和隐蔽性[4]是评价一种图像水印方案是否可行的标准.鲁棒性指水印抵抗各种图像处理操作或攻击的能力，隐蔽性指水印图像和原始图像之间的差异.为了保证鲁棒性，水印方案需要有更多有效的版权信息被嵌入.基于奇异值分解(Singular Value Decomposition, SVD)[5]的数字水印具有较高的信息容量，且对隐蔽性几乎没有影响.为此，学者提出了多种基于SVD和DWT的混合方案，例如，[6]提出一种基于SVD和DWT的主成分小波域水印算法.然而，其将水印嵌入主成分中，导致较弱的隐蔽性与鲁棒性.[7]提出一种SVD和整数小波变换(Integer Wavelet Transform, IWT)的水印方案，并将水印嵌入各频带奇异值中.然而其没有最优化比例因子，这为隐蔽性和鲁棒性方面提供了改进的余地.

本文提出一种基于SVD和IWT的图像水印方案.首先，对宿主图像进行IWT，然后对变换获得的各频带进行SVD，并根据比例因子进行水印嵌入.为了进一步提高水印质量，使用粒子群优化(Particle Swarm Optimization, PSO)算法获得最优比例因子.与现有相关方案相比，以峰值信噪比(Peak Signal-Noise Ratio, PSNR)和归一化相关性作为评估指标，结果表明本文方案在测试图像上表现出优越的鲁棒性和隐蔽性.

1 相关知识

1.1 奇异值分解(SVD)

SVD是一种将对称矩阵对角化的线性代数技术.数字图像也可视为一个整数矩阵，所以可以直接在数字图像上进行SVD.SVD将给定矩阵分解成三部分，即左奇异矩阵U、右奇异矩阵V和奇异矩阵S.其中，矩阵S仅包含对角元素，称为奇异值，矩阵U和V包含图像分解的详细信息[8].假设A是一个n维矩阵，那么矩阵S可以有最大n个对角元素.母矩阵A可以用矩阵S的少量元素再生，但是这个再生的矩阵AS将导致其质量下降.矩阵U和V遵循下列约束条件：UUT=In和VVT=In.对角矩阵S的对角线元素遵循下式：d1≥d2≥…≥dr≥dr+1≥dr+2≥…>dn=0.其中，r(≤n)代表矩阵S的秩，d1,d2,…,dn为矩阵S的对角线元素.

1.2 整数小波变换(IWT)

经典小波变换在假设输入为浮点型数据下执行变换，但在现实中，许多应用程序(如图像水印)只涉及整数输入，所以，可以由整数到整数的小波变换来消除浮点数转换成整数的误差.可通过修改分解、预测和更新三个基本步骤来应用IWT，步骤如下[9]：

分解：将原始信号(C)分解为偶数(Ce)和奇数(Co)部分.

预测：在基于偶数序列下预测得到奇数序列，奇数序列预测值与实际值之间的差用做下一层整数小波变换的新奇数序列.

更新：将预测的奇数样本与原始偶数样本相结合，更新产生一个新偶数样本来确保新样本具有相同功能.

2 提出的水印方案

2.1 水印嵌入过程

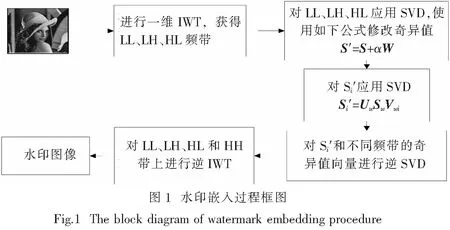
水印嵌入过程如图1所示.具体步骤如下：

(1) 使用IWT将宿主图像H变换到小波域，将获得的LL,LH和HL频带作为嵌入频带.

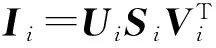
(1)

(3) 根据式(2)修改每个频带的奇异值，其中α代表比例因子，W代表水印,

Si′=Si+αW.

(2)

(4) 根据式(3)对Si′进行另一次SVD,Si′=UwiSwiVwiT.

(3)

(5) 利用矩阵Swi以及Ui、Vi，为每个模块生成水印子带Iwi，如式(4)所示：

Iwi=UiSwiViT.

(4)

(6) 将水印子带Iwi进行逆IWT，生成水印图像HW.

2.2 水印萃取过程

从失真水印图像HW*中萃取水印的过程如图2所示.具体步骤如下：

(1) 首先，对水印图像进行一维IWT得到IW*和LL,LH，HL频带.

(2) 根据式(5)在水印图像中的LL,LH，HL频带上进行SVD,

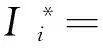
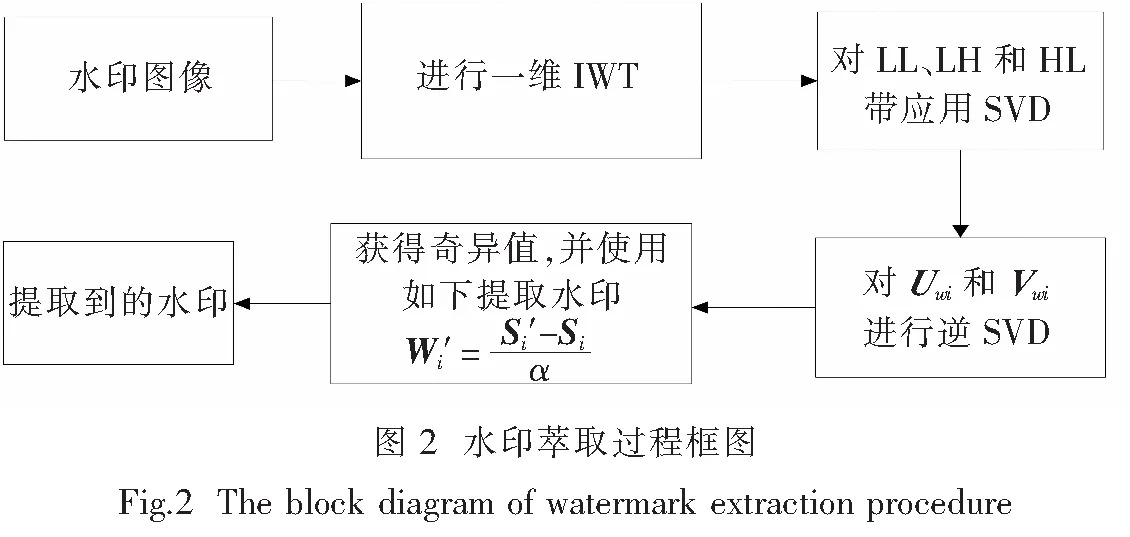
(3) 根据式(6)，对矩阵Uwi和Vwi进行逆SVD，在LL,LH和HL频带上得到S′的近似值,

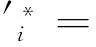
(6)

(4) 根据式(7)可以得到LL,LH和HL频带上水印的近似值,

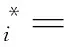
(7)

(5) 萃取过程结束.

2.3 采用PSO优化比例因子

PSO算法[10]是一种基于群体智能的随机优化算法，粒子群中的每一个粒子代表一种可行解，粒子在整个解空间中运动，逐渐向最优个体靠拢，最终找出最优解.

从本文嵌入过程和萃取过程可以看出，提出方案的隐蔽性和鲁棒性在很大程度上依赖于比例因子α.较小的α值可以提供较好的隐蔽性，但鲁棒性较差；而较大的α值则相反.因此，本文利用PSO算法来寻找最优比例因子α，从而均衡隐蔽性与鲁棒性.本文利用归一化相关性来表示水印的鲁棒性，定义如下：

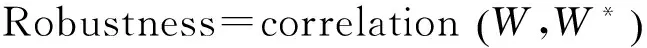
(8)

相关性函数correlation()定义如下：

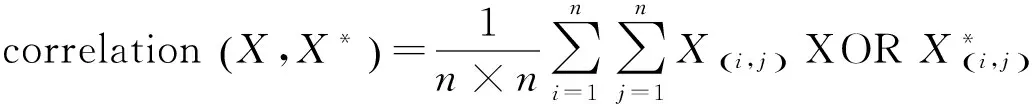
(9)

其中，H为宿主图像，其尺寸为n×n，HW为水印图像，W为原始水印，W*为萃取的水印.假设水印图像有N种攻击且可插入M频带中，那么方案的平均鲁棒性表示为：

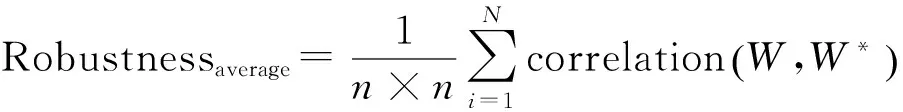
(10)

本文利用PSNR来表示水印的隐蔽性.PSNR反映了水印图像与宿主图像的相似性，PSNR越高说明嵌入水印后的图像越接近原始图像，即水印隐蔽性越好.假设宿主图像(X)和水印图像(X*)的大小均为n×n，并且它们均可以达到最大像素Xmax，那么PSNR可以定义为：

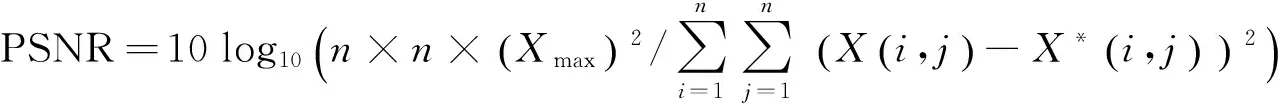
(11)

本文优化目标为均衡隐蔽性和鲁棒性，为了构建一个适应度函数,设定Nor(PSNR)为归一化的PSNR值，所以适应度函数表示如下：

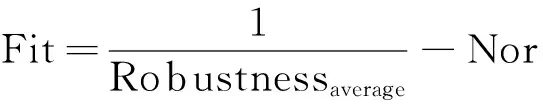
(12)

每一个比例因子被视作一个大小为256的粒子向量.由于PSO算法是现有较为成熟的智能优化算法，这里将不再描述其具体过程.对于本文中PSO算法的参数，设置粒子种群大小为20，最大迭代数设为100，学习因子C1=C2=2.

3 实验及分析

3.1 实验设置

实验中，采用3个灰度图像“李娜”“房屋”和“辣椒”(大小均为512×512)作为宿主图像，一个大小为512×512的灰度标度图像W1作为水印图像，宿主图像和水印图像如图3所示.

3.2 实验结果

将本文方案与[7]和[6]方案进行比较，三种方法的相同点和不同点如表1所示.尽管[7]使用IWT+SVD，但其使用了所有子带且没有最优化比例因子.

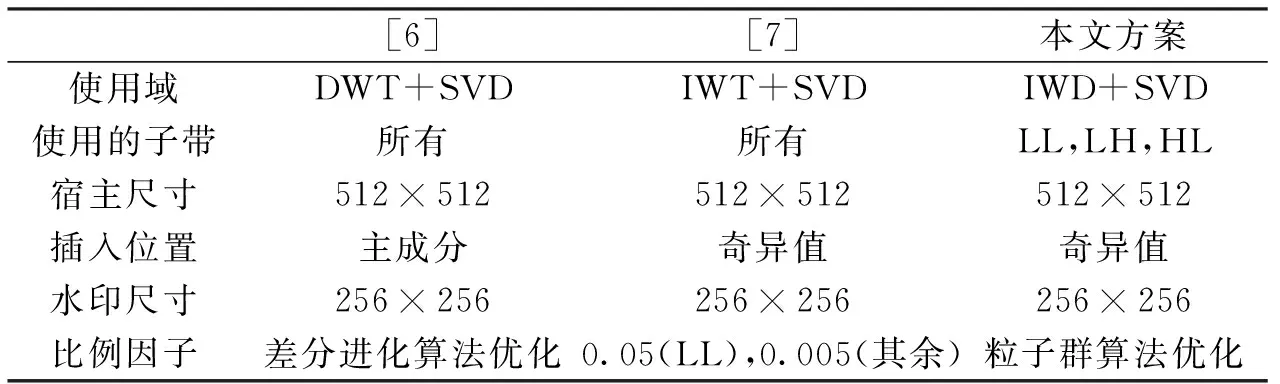
表1 本文方法与其他方法的技术区别Tab.1 The difference between proposed method with other methods

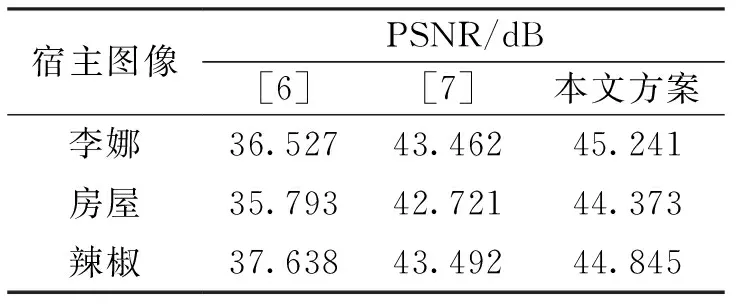
表2 不同方案中水印嵌入后图像的峰值信噪比Tab.2 The peak signal to noise ratio of different scheme after embedded watermark image

宿主图像PSNR/dB[6][7]本文方案李娜36.52743.46245.241房屋35.79342.72144.373辣椒37.63843.49244.845

表2列出了不同方案中，插入水印W1后，图像的PSNR.可以看出，本文方案具有最高的PSNR.这说明本文方案水印嵌入后的水印图像与原始图像最为接近，即水印隐蔽性最好.

目前，针对水印图像的攻击有很多种，大体可分为加噪声、低通滤波、比例缩放、剪裁、旋转等.图4举例显示了对嵌入水印′W1′的水印图像“李娜”进行噪声和旋转攻击后的图像，图5显示了经过攻击后从LL、LH和HL频带萃取的水印′W1′.

表3给出了在图像“李娜”中存在不同攻击时，各种水印方案中原始水印和萃取水印的相关性，即水印方案的鲁棒性比较.其中，[7]和[6]的值为其所有频带相关性最好的值，本文方案的值为LL、LH和HL频带中相关性最好的值.可以看出，本文方案在各种攻击下，水印图像的鲁棒性最好.在[6]方法中，利用主成分来代替奇异值进行水印插入，虽然能够消除虚警问题，但也降低了方案的鲁棒性和隐蔽性.这是因为，随着主成分的改变，会引发奇异矩阵的改变，而奇异矩阵包含着大量图像信息，导致较低的鲁棒性.由于本文方案在奇异值中插入水印，所以在相关性或鲁棒性以及峰值信噪比方面优于[6]方案.另外，由于本文方案使用粒子群算法优化比例因子，所以在隐蔽性和鲁棒性方面优于[7]方案.

表3 各种水印方案的鲁棒性比较Tab.3 The robustness comparison of all kinds of watermarking schemes

本文方案的性能在其他2个宿主图像(“房屋”和“辣椒”)上也进行了测试，在隐蔽性和鲁棒性方面，与在图像“李娜”上的实验结果相似.

4 结束语

本文提出一种基于IWT和SVD的图像水印方案，同时融入了PSO来优化水印嵌入的比例因子.将宿主图像进行IWT变换，并在每个频带上进行奇异值分解，根据最优比例因子将水印嵌入奇异值中.与相关方案的比较结果证明，本文方案水印在保持高隐蔽性的同时，对常见图像处理操作也具有很好的鲁棒性.

[1] 雷蕾, 郭树旭, 王雷. 基于小波变换的SVD数字图像水印算法研究[J]. 计算机仿真, 2013, 30(9):169-172.

[2] 杜肖山, 廖述剑. 一种DWT与DCT相结合的图像水印算法[J]. 计算机技术与发展, 2011, 21(1):147-150.

[3] 蔡宜嘉, 牛玉刚, 苏庆堂. 基于DWT-SVD和Fibonacci变换的彩色图像盲水印算法[J]. 计算机应用研究, 2012, 29(8):3025-3028.

[4] HAI T, LI C, ZAIN J M, et al. Robust image watermarking theories and techniques: a review[J]. Journal of Applied Research & Technology, 2014, 12(1):122-138.

[5] ALI M, CHANG W A, PANT M. A robust image watermarking technique using SVD and differential evolution in DCT domain[J]. Optik - International Journal for Light and Electron Optics, 2014, 125(5):428-434.

[6] ALI M, CHANG W A. An optimized watermarking technique based on self-adaptive DE in DWT-SVD transform domain[J]. Signal Processing, 2014, 94(1):545-556.

[7] MAKBOL N M, KHOO B E. A new robust and secure digital image watermarking scheme based on the integer wavelet transform and singular value decomposition[J]. Digital Signal Processing, 2014, 33(4):134-147.

[8] 周立, 柳春华, 蒋天发. 基于小波变换和奇异值分解的图像水印算法[J]. 武汉大学学报:工学版, 2011, 44(1):120-123.

[9] 邱群, 马小虎. 采用整数小波变换和多目标遗传算法的可逆灰度水印[J]. 计算机辅助设计与图形学学报, 2015, 27(7):1290-1297.

[10] TSAI H H,HUANG Y J, LAI Y S. An SVD-based image watermarking in wavelet domain using SVR and PSO[J]. Applied Soft Computing, 2012, 12(8):2442-2453.

责任编辑：龙顺潮

Robust and Invisible Digital Image Watermarking Scheme Based on IWT and SVD

LIAOHong-jian1*,HUANGLiang-yong1,2

(1.College of Mathematics and Computer Science, Guangxi Science & Technology Normal University, Laibin 546199；2.College of Information Engineering, Wuhan University of Technology, Wuhan 410082 China)

To resolve the problem of the robustness and invisibility of digital image watermarking, an image watermarking scheme based on integer wavelet transform (IWT) and singular value decomposition (SVD) is proposed. Firstly, the host image is transformed into wavelet domain by using integer wavelet transform. Then, the singular value decomposition is performed on each frequency band, and the watermark is embedded into the singular value according to the scaling factor. Finally, the optimal scaling factor is obtained by using the particle swarm optimization (PSO) algorithm under the tradeoff between robustness and invisibility. Experimental results show that the proposed watermarking scheme is robust to common image processing operations, while maintaining excellent concealment.

image watermarking; integer wavelet transform; singular value decomposition; ant colony optimization

2016-03-18

广西高校科研项目(LX2014500)；柳州市科技课题(2014C030402)；来宾市科技攻关课题(143620)

廖洪建(1977-)，男，湖南 慈利人，副教授.E-mail:lhj181275@163.com

TP391

A

1000-5900(2016)03-0059-05