应变下氮和硼替位掺杂石墨烯的结构与电子性质*

熊扬虹, 彭 琼, 李 金, 张春小, 唐 超, 钟建新

(湘潭大学 物理与光电工程学院，微纳能源材料与器件湖南省重点实验室，湖南 湘潭 411105)



应变下氮和硼替位掺杂石墨烯的结构与电子性质*

熊扬虹, 彭 琼, 李 金, 张春小, 唐 超, 钟建新*

(湘潭大学 物理与光电工程学院，微纳能源材料与器件湖南省重点实验室，湖南 湘潭 411105)

采用第一性原理计算方法，研究了氮(N)和硼(B)替位掺杂石墨烯在加载应变情况下的结构和电子性质.计算结果表明(采用6×6超原胞)，对于纯石墨烯，当应变大于临界应变30%时发生从弹性应变至非弹性应变的转变，体系总能在转变处发生突变.而N和B掺杂石墨烯的临界应变分别变为17.6%和17.4%，这表明掺杂石墨烯的弹性应变范围大幅减小.通过研究纯石墨烯和N/B替位掺杂石墨烯的电子性质，发现纯石墨烯在对称应变下仍为零带隙，而掺杂后费米能级处出现电子态，体系转变为金属，并且发现应变可以调节掺杂石墨烯的费米能级但不能在狄拉克锥处打开带隙.

第一性原理;石墨烯;应变;掺杂

由于热力学涨落，科学家们一直认为任何二维晶体都不能在有限的温度中存在[1-2].然而，2004年，英国曼切斯特大学的NOVOSELOV K S等在实验室用微机械剥离方法成功制备出了石墨烯，证明了单原子层厚的二维晶体能够稳定存在[3-4]，这一发现引起了物理、化学及电子学科研究者们极大的兴趣.石墨烯具有优良的力学性能，是现在世界上已知最为坚硬的材料，其弹性系数为105N/m，杨氏模量达到0.5 TPa[5].此外，石墨烯还具有奇异的电学性质，如高达200 000 cm2/V·s的载流子迁移率[6-10]和仅有10-6Ω·cm的电阻率[8,11-13]，以及反常的量子霍尔效应[8,14-15]、完美的电子遂穿效应[16-17]和弱的安德森局域[17]等优异性质.这些优良的性能使得石墨烯在微纳电子[18]、传感器[19]和储氢[20]等诸多方面有着广阔的应用前景.实验上，人们采用微机械剥离法、还原氧化石墨法、表面或外延生长法、化学气相沉积法、有机物合成生长法等方法制备石墨烯[21-25].

由于石墨烯是零带隙的半金属，不能直接应用于纳米尺度电子器件中，所以如何有效地控制其电子结构是应用中最重要的一环.调制石墨烯电子性质的方式有很多种，如吸附[26]、缺陷[27]、施加应变[28-29]、掺杂[30]、裁剪成纳米带[31]等.人们对于石墨烯掺杂做了很多的研究，PANCHAKARLA等人在实验上成功制备了N原子和B原子掺杂的材料，并且发现通过氮(硼)掺杂可以获得n(p)-石墨烯半导体，并可以通过掺杂浓度调节其性质[30].RANI P等人基于第一性原理研究了N和B掺杂对石墨烯的能带带隙的调制[32]，发现掺杂能够打开石墨烯的带隙.但是，FAN X F[33]等通过第一性原理研究发现，当在3n×3n的石墨烯超原胞中引入N(B)的替位掺杂时并不能打开带隙.这些研究表明，N(B)掺杂可以调节石墨烯的结构和物理性质，可以扩展石墨烯的应用.但是，在实际应用中，由于与衬底或其他环境的作用，都会给石墨烯带来形变，同时这种形变也会对其物理性质产生影响，因此对N(B)掺杂石墨烯在应变之下的结构和电子性质的研究非常重要.本文采用基于密度泛函理论的第一性原理计算方法，研究了N(B)掺杂石墨烯在应变之下的结构和电子性质，希望为掺杂石墨烯的实际应用提供有价值的理论依据.

1 方法与模型

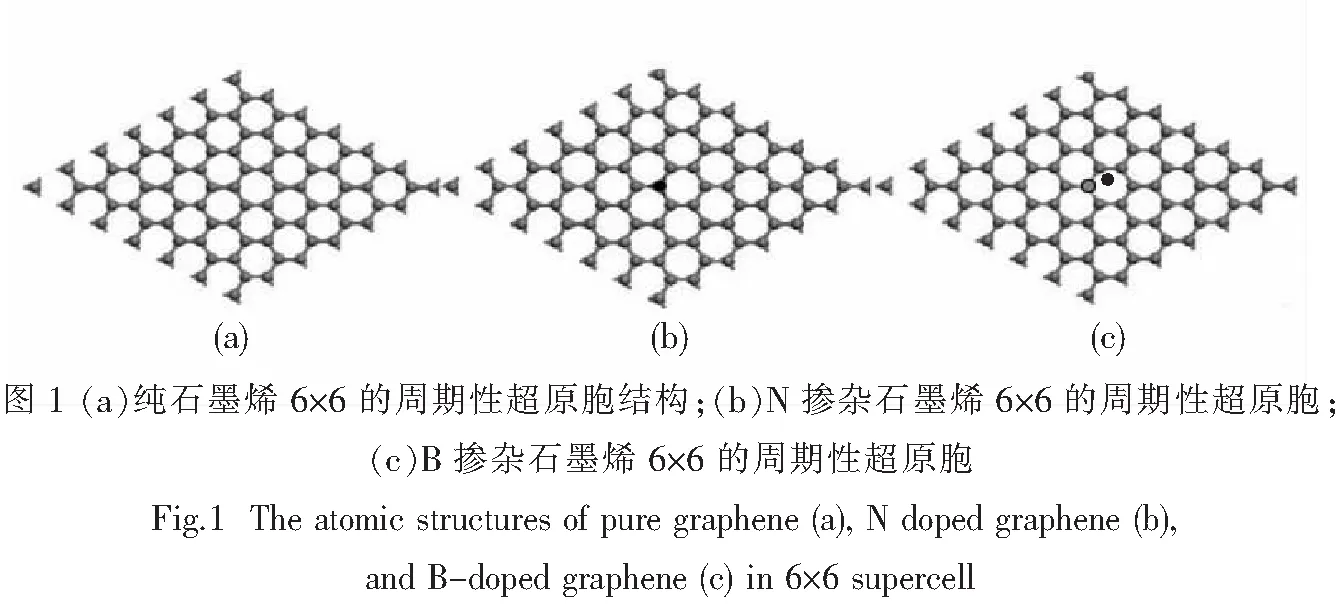
本工作中采用的是基于密度泛函理论[34]的第一性原理的计算方法，计算通过VASP(Vienna Abinitio Simulation Package)软件包[35]来完成的.计算中，价电子与离子实之间的相互作用通过PAW(Projector Augmented Wave)方法[36]来描述，其中交换关联泛函选择的是局域密度近似LDA(Local Density Approximation). 平面波截断能选取为400 eV，在弛豫中采用以Γ点为中心的Monkhorst-Pack方法划分K点网格5×5×1，在静态计算和态密度计算中以同样的方式分别划分K点网格9×9×1，9×9×1.电子的自洽迭代计算的能量收敛标准为10-6eV,弛豫过程中力的收敛精度为-10-3eV/nm.在模拟二维石墨烯片时，采用的是包含72个原子的6×6周期性超原胞结构，为了消除相邻两层石墨烯纳米片之间的相互作用，真空层的大小取为1.5 nm.初始结构见图1(a).掺杂是调节石墨烯电子性质的一种行之有效的方法.掺杂同样采用6×6的周期性超原胞，分别用N和B原子替换超原胞中心的一个C原子，图1(b)～(c)分别为N和B掺杂石墨烯的6×6周期性超原胞结构.

首先，我们研究了对称应变对各个石墨烯体系的电子结构的调控行为，所谓的对称应变是指在保持二维石墨烯的正六角晶格结构不变的情况下，对原胞进行整体的放大或缩小.其应变公式为：

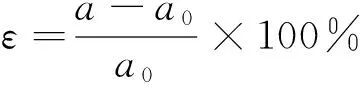
(1)

其中a0和a分别为施加应变前后体系的晶格常数.在对称应变的条件下，原胞保持正六边形的结构不变，只要在不同的晶格常数下弛豫原子的位置即可.当晶格常数大于无应变条件下的晶格常数a0时，对应于拉伸状态;当晶格常数小于a0时，对应于压缩的状态.由于我们研究的是N和B掺杂石墨烯纳米片在拉伸应变下的结构和电子性质，因此只需在晶格常数大于a0时，对体系进行拉伸状态的弛豫计算.

2 结果与讨论

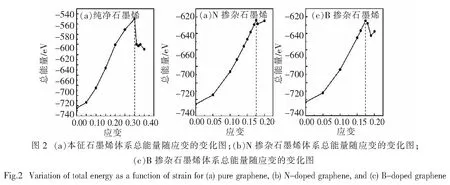
首先，我们对本征石墨烯、N掺杂石墨烯和B掺杂石墨烯体系进行了结构优化，得到了平衡状态下各个体系的晶格常数：本征石墨烯体系的晶格常数为1.468 3 nm；N掺杂石墨烯体系的晶格常数为1.466 3 nm； B掺杂石墨烯体系的晶格常数为1.471 3 nm.与本征石墨烯相比，N掺杂石墨烯的晶格常数减小，B掺杂石墨烯的晶格常数增大，这与PANCHAKARLA[30]等人的实验研究结果相符.接着，我们研究了各体系的总能量随应变的变化趋势，结果如图2所示.从图2(a)中可以看出，在小于30%应变下，本征石墨烯体系总能量随着应变的增大逐渐地增大；而当应变为30%时体系的总能发生了突变，这表明纯净石墨烯体系在应变大于30%的情况下不再处于弹性应变范围，即小于等于30%的应变为弹性应变，而大于30%的应变为非弹性应变.这个结果与TOPSAKAL M等人的研究工作[37]一致.而从图2(b)中可以得到，N原子掺杂石墨烯体系的临界应变为17.6%，在应变小于17.6%时，掺杂体系的总能量随着所施加应变的增大而逐渐增大，当应变增大到17.6%时，掺杂体系的总能量发生突变，体系进入非弹性应变区域.小于等于17.6%的应变为弹性应变，大于17.6%的应变为塑性应变.同样地，从图2(c)中可以看出，B原子掺杂石墨烯体系在小于17.4%的应变下，总能量随应变的增大而逐渐增大.当应变增大到17.4%时，掺杂体系的总能量发生突变，临界应变为17.4%，体系在大于17.4%的应变下进入非弹性应变区域.由此可得出结论，掺杂后体系的弹性应变范围大幅减小.

为了清晰地说明不同对称拉伸应变条件下体系的结构和成键特性的变化情况，我们通过分析电子局域化函数(Electron Localization Function，ELF)来对体系进行成键分析.图3是各石墨烯体系在不同应变下的电子局域化函数图，电子局域化函数值从0到1连续变化.图3(a)～(c)是不同应变下纯净石墨烯体系的电子局域化函数图.从图3(a)中可以看到，每个碳原子与其最近邻的3个碳原子都有3个吸引子，这说明C和C原子之间存在很强的共价键作用.当应变增大至25%，本征石墨烯体系每个碳原子与其最近邻的3个碳原子仍有3个吸引子，体系仍然保持原来的成键特征，但吸引子有所伸长,对应于图3(b).这是因为原子间距离的变大使得电子运动范围扩大，从而导致吸引子的形状发生明显的变化.而当应变进一步增大至45%时(大于30%的非弹性应变)，纯石墨烯体系的碳原子之间的吸引子出现明显的分离现象，电子高局域化区域移向各个碳原子的周围，如图3(c)所示.图3(d)～(f)为N掺杂石墨烯体系在不同应变下的电子局域化函数图.同样地，在小于等于临界应变17.6%时体系能保持六角晶格不变，对应于图3(d)～(e).每个碳原子(或者氮原子)与其最近邻的3个碳原子(或者氮原子)都有3个吸引子，这说明C和N(或C)原子之间存在很强的共价键作用，但是C—N键之间吸引子的形状和位置都明显的偏向N原子，说明由于碳和氮电负性的差异，使得C—N键表现出极性共价键的特点.在大于临界应变17.6%时，石墨烯的六角蜂窝状结构被破坏，C—N键完全断裂，原子键形成原子链或团簇，如图3(f)所示.图3(g)～(i)为B掺杂石墨烯体系在不同应变下的电子局域化函数图.从图3(g)～(h)可以看出，每个碳原子(或者硼原子)与其最近邻的3个碳原子(或者硼原子)都有3个吸引子，C和B(或C)原子之间存在很强的共价键作用，但是C-B键之间吸引子的形状和位置都明显的偏向C原子，碳硼共价键表现很强的极性.在大于17.4%的应变下，掺杂体系不再保持原来的成键特征，此时的C—B键已经断裂，体系进入非弹性应变范围，原子键形成原子链或团簇，见图3(i).

图4(a)为无应变下纯石墨烯的能带结构和态密度图.从能带图上可以看到，石墨烯的Dirac点在布里渊区的Γ点，价带和导带在费米能级相接，这是由于在采用6×6的超原胞时，布里渊区折叠使Dirac点从单胞时的K点折叠到了Γ点[33].图4(b)～(d)分别为10%应变、25%应变和30%应变下本征石墨烯的能带结构和态密度图，发现对称应变不能打开带隙.通过分析分态密度，发现本征石墨烯在费米能级附近的电子态主要是碳原子的pz态所贡献的.

图4(f)～(j)分别为N掺杂石墨烯体系无应变、10%应变、15%应变、17.6%应变和18%应变下的能带结构和态密度图.图4(k)～(o)分别为B掺杂石墨烯体系在无应变、10%应变、15%应变、17.4%应变和20%应变下的能带结构和态密度图.对比图4(f)和(a)、图4(k)和(a)，我们发现掺杂N原子导致费米能级上移，而掺杂B原子导致费米能级下移，这是由于当一个C原子被N(B)原子替换时，会使体系多出(减少)一个公有化电子，从而使得体系的费米能级发生朝上(下)移动.从图4(f)和图4(k)中可以发现N/B原子掺杂并未打开带隙，这是由掺杂后的石墨烯对称性破坏和Dirac点附近的电子态的杂化所致，基于6×6超原胞的计算结果验证了在3n×3n的石墨烯超原胞中引入N(B)的替位掺杂时并不能打开带隙的结论[33].从图4(f)和(i)以及图4(k)和(n)可以看出掺杂后费米能级出现电子态，石墨烯转变为金属，这是由于费米能级移动所致.从图4(f)～(j)可以发现，随着应变的增大，N掺杂石墨烯的能带结构越来越平缓，在20%应变(非弹性应变)时趋于直线，对应于前文电子局域化函数的分析——在大于临界应变17.6%时，石墨烯的六角蜂窝状结构被破坏，C—N键完全断裂，能带结构表现出原子能级的特征.同样由图4(k)～(o)可知，随着应变的增大，B掺杂石墨烯的能带结构也越来越平缓，在20%应变(非弹性应变)时趋于直线.此外，从能带图上还可以发现，在应变之下，费米能级的相对位置也会发生变化.从图4(f)～(j)和图4(k)～(o)中的态密度分布可以看出，在N和B掺杂情况下，加载应变均不能在Dirac处打开能隙.通过对态密度的进一步分析，发现掺杂石墨烯在弹性应变下，费米能级附近的电子态峰主要由C原子的pz态和掺杂原子(N/B)的pz态耦合而成.而在临界应变之后，情况不一样，对于N掺杂石墨烯，费米能级附近的电子态峰主要是由C原子的pz、px态和N原子的px、py态的贡献；对于B掺杂石墨烯，费米能级附近的电子态峰主要是由C原子的pz态和B原子的px、pz态的贡献.

3 结 论

采用第一性原理方法，研究了硼和氮替位掺杂石墨烯在加载应变情况下的结构和电子性质.计算结果表明，本征石墨烯的最大弹性应变范围为30%，而N(B)掺杂石墨烯的临界应变为17.6%(17.4%)，表明掺杂后体系的弹性应变范围显著减小.通过对本征石墨烯和掺杂石墨烯电子性质的研究，发现在对称应变下本征石墨烯体系保持零带隙不变，而在进行氮(硼)原子的替位掺杂之后，费米能级处出现电子态，石墨烯体系从零带隙半金属转变为金属,并且应变对N(B)掺杂石墨烯的费米能级有调节作用.

[1] GONZALEZ J, GUINEA F, HERRERO J. Propagating, evanescent, and localized states in carbon nanotube-graphene junctions[J]. Phys Rev B, 2009, 79(16): 165434.

[2] GRUNEIS A, ATTACCALITE C, WIRTZ L,et al. Tight-binding description of the quasiparticle dispersion of graphite and few-layer graphene[J]. Phys Rev B, 2008, 78(20): 205425.

[3] NOVOSELOV K S, GEIM A K, MOROZOV S V, et al. Electric field effect in atomically thin carbon films[J]. Science, 2004, 306(5696): 666-669.

[4] BAE S, KIM H, LEE Y, et al. Roll-to-roll production of 30-inch graphene films for transparent electrodes[J]. Nat Nanotechnol, 2010, 5(8): 574-578.

[5] LEE C, WEI X D, KYSAR J W, et al. Measurement of the elastic properties and intrinsic strength of monolayer graphene[J]. Science, 2008, 321(5887):385-388.

[6] HU L, HECHT D S, GRUNER G. Infrared transparent carbon nanotube thin films[J]. Appl Phys Lett, 2009, 94(8): 81103.

[7] JEE H, HAN J H, HWANG H N, et al. Pentacene as protection layers of graphene on SiC surfaces[J]. Appl Phys Lett, 2009, 95(9): 93107.

[8] NOVOSELOV K S, GEIM A K, MOROZOV V S, et al. Two-dimensional gas of massless Dirac fermions in graphene[J]. Nature, 2005, 438(7065): 197-200.

[9] WU M, LIU E Z, GE M Y, et al. Stability, electronic, and magnetic behaviors of Cu adsorbed graphene: A first-principles study[J]. Appl Phys Lett, 2009, 94(10): 102505.

[10] TOMBROS N, JOZSA C, POPINCIUC M, et al. Electronic spin transport and spin precession in single graphene layers at room temperature[J]. Nature, 2007, 448 (7153): 571-574.

[11] ZHANG Y, TAN Y W, STORMER H L, et al. Experimental observation of the quantum Hall effect and Berry's phase in graphene[J]. Nature, 2005, 438(7065): 201-204.

[12] LIU G, STILLMAN W, RUMYANTSEV S, et al. Low-frequency electronic noise in the double-gate single-layer graphene transistors[J]. Appl Phys Lett, 2009, 95(3): 33103.

[13] LU G, OCOLA L E, CHEN J. Gas detection using low-temperature reduced graphene oxide sheets[J]. Appl Phys Lett, 2009, 94(8): 83111.

[14] GUILLEMETTE J, SABRI S S, WU B X, et al. Quantum hall effect in hydrogenated graphene[J]. Phys Rev Lett, 2013, 110(17): 176801.

[15] GUSYNIN V P, SHARAPOV S G. Unconventional integer quantum hall effect in graphene[J]. Phys Rev Lett, 2005, 95(14): 146801.

[16] KATSNELSON M I, NOVOSELOV K S, GEIM A K. Chiral tunnelling and the Klein paradox in graphene[J]. Nature Phys, 2006, 2(9): 620-625.

[17] MOROZOV S, NOVOSELOV K, KATSNELSON M, et al. Charge and spin hall conductivity in metallic graphene[J]. Phys Rev Lett, 2006, 97(10): 16801.

[18] SRINIVASAN C, SARASWATHI R. From graphite to graphene and now to graphene[J]. Curr Sci, 2009, 97(3): 302-303.

[19] DATTA S S, STRACHAN D R, MELE E J, et al. Surface potentials and layer charge distributions in few-layer graphene films[J]. Nano Lett, 2009, 9(1):7-11.

[20] BERCIAUD S, RYU S, BRUS L E, et al. Probing the intrinsic properties of exfoliated graphene: Raman spectroscopy of free-standing monolayers[J]. Nano Lett, 2009, 9(1): 346-352.

[21] GILJE S, HAN S, WANG M, et al. A chemical route to graphene for device applications[J].Nano Lett, 2007, 7(11): 3394-3398.

[22] SCHNIEPP H C, LI J L, MCALLISTER J M, et al. Functionalized single graphene sheets derived from splitting graphite oxide[J]. J Phys Chem B, 2006, 110(17):8535-8539.

[23] BERGER C, SONG Z, LI X, et al. Electronic confinement and coherence in patterned epitaxial graphene[J].Science, 2006, 312(5777):1191-1196.

[24] STANKOVICH S, DIKIN D A, PINER R D, et al. Synthesis of graphene-based nanosheets via chemical reduction of exfoliated graphite oxide[J]. Carbon, 2007, 45(7):1558-1565.

[25] STANKOVICH S, DIKIN D A, DOMMETT G H B, et al. Graphene-based composite materials[J]. Nature, 2006, 442(7100): 282-286.

[26] BALOG R, JORGENSEN B, NILSSON L, et al. Bandgap opening in graphene induced by patterned hydrogen adsorption[J]. Nat Mater, 2010, 9(4): 315-319.

[27] OKADA S, KAWAI T, NAKADA K. Electronic structure of graphene with a topological line defect[J]. J Phys Soc Jpn, 2011, 80(1): 13709.

[28] GUI G, LI J, ZHONG J X. Band structure engineering of graphene by strain: First-principles calculations[J]. Phys Rev B, 2008, 78(7): 75435.

[29] WONG J H, WU B R, LIN M F, et al. Strain effect on the electronic properties of single layer and bilayer graphene[J]. J Phys Chem C, 2012, 116 (14):8271-8277.

[30] PANCHAKARLA L S, SUBRAHMANYAM K S, SAHA S K, et al. Synthesis, structure, and properties of boron-and nitrogen-doped graphen[J]. Adv Mater, 2009, 21(46): 4726-4730.

[31] SON Y W, COHEN M, LOUIE S. Half-metallic graphene nanoribbons[J]. Nature, 2006, 444(7117): 347-349.

[32] RANI P, JINDAL V K. Designing band gap of graphene by B and N dopant atoms[J]. RSC Adv, 2013, 3(3): 802-812.

[33] FAN X F, SHEN Z, LIU A Q, et al. Band gap opening of graphene by doping small boron nitride domains[J]. Nanoscale, 2012, 4(6):2157-2165.

[34] KOHN W, SHAM L J. Self-consistent equations including exchange and correlation effects[J]. Phys Rev, 1965, 140(4A): A1133-A1138.

[35] KRESSE G, FURTHMüLLER J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set[J]. Phys Rev B, 1996, 54(16): 11169-11186.

[36] BLÖCHL P E. Projector augmented-wave method[J]. Phys Rev B, 1994, 50(24): 17953-17979.

[37] TOPSAKAL M, CAHANGIROV S, CIRACI S. The response of mechanical and electronic properties of graphane to the elastic strain[J]. Appl Phys Lett, 2010, 96(9): 91912.

责任编辑：罗 联

Structural and Electronic Properties of the Nitrogen and Boron Doped Graphene under Strain

XIONGYang-hong，PENGQiong，LIJin，ZHANGChun-xiao，TANGChao，ZHONGJian-xin*

( Hunan key Laboratory for Micro-Nano Energy Materials and Devices,School of Physics and Optoelectronics, Xiangtan University, Xiangtan 411105 China)

Structural and electronic properties of the nitrogen (N) and boron (B) doped graphene under strain have been studied by the first-principles method. The results show that, the pure graphene undergoes a transition from elastic deformation to non-elastic deformation as the strain is larger than 30% with an abrupt energy drop of the system. For N doped and B doped graphene, the critical strains for the transition of elastic to non-elastic deformation are 17.6% and 17.4% respectively, indicating that the structural stability of the doped graphene is significantly reduced. For the electronic properties of the pure graphene and N/B doped graphene, we found that the pure graphene under symmetrical strain remains its zero band gap, while the N/B doped graphene changes from a semimetal to a metal with finite density of states at the Fermi level. In addition, we found that the strain can adjust the Fermi level of the doped graphene but cannot open a gap at the Dirac cone.

first principles；graphene；strain；doping

2016-04-18

国家重点基础研究发展计划(2012CB921303);国家自然科学基金项目(4040204)；国家自然科学基金青年科学基金项目(11404275，11304263，11204260)；国家自然科学基金理论物理专项基金(11347206)；湖南省教育厅一般项目(14C1095)

钟建新(1964-)，男，湖南 新宁人，博士，教授，博士生导师. E-mail:jxzhong@xtu.edu.cn

O469

A

1000-5900(2016)03-0011-06