微分求积法在弹性压应力波下直梁的动力压曲稳定分析中的应用*

汪亚运， 陈得良， 彭旭龙， 周 露

(长沙理工大学 土木与建筑学院，湖南 长沙 410004)



微分求积法在弹性压应力波下直梁的动力压曲稳定分析中的应用*

汪亚运， 陈得良*， 彭旭龙， 周 露

(长沙理工大学 土木与建筑学院，湖南 长沙 410004)

基于欧拉-伯努利梁理论及能量守恒原理，建立了直梁压曲稳定微分控制方程及其应力波波前附加边界条件，对应力波反射前等截面梁屈曲与压应力波耦合动力屈曲问题进行了研究.利用微分求积法(DQM)并结合边界条件，将直梁压曲稳定控制微分方程离散成线性代数方程组，进而得到了系统的动力屈曲特征方程，并研究了加载端简支远端固支梁在压应力波反射前的动力屈曲问题.数值研究表明该方法具有可靠的精度和收敛性.

等截面直梁；压应力波；微分求积法；动力屈曲

杆件的动力屈曲问题一直以来受到学者的广泛关注，取得了一定的研究成果.王安稳等[1]利用应力波理论和失稳瞬间能量转换守恒，推导出了直杆动力分岔的能量准则，进一步得到了失稳时压缩波前的附加约束条件，并计算得到了梁屈曲与压应力波耦合动力屈曲的理论解.韩大伟等[2]基于双频特征参数法和应力波理论得到了矩形薄板在面内轴向冲击荷载作用下动力屈曲位移的解析解.并在[3]中基于应力波理论，用半解析半数值方法对轴向时变冲击载荷作用下的直杆弹性动力屈曲问题进行了研究.毛柳伟等[4]采用能量守恒原理，根据屈曲时刻能量的转换关系，利用微分中值定理得到了和[1]一致的弹性直杆屈曲控制方程和波前边界条件.此外，毛柳伟等[5-7]基于双特征参数理论和最优模态的方法提出了相应的数值方法，研究了应力波作用下直杆的动力屈曲问题，并得到了可靠的结果.

基于上述已有理论，本文将采用微分求积法(DQM)来求解加载端简支远端固支等截面梁动力屈曲问题.微分求积法是一种求解微分方程的数值方法，广泛应用于工程结构稳定性和自由振动研究领域[8-13].文中通过微分求积法将直梁控制微分方程和边界条件离散成线性代数方程组，继而得到动力屈曲特征方程.并结合静力和动力屈曲分析，验证了该方法在求解直梁屈曲和压应力波耦合动力屈曲问题中的精度和收敛性.

1 微分控制方程及边界条件

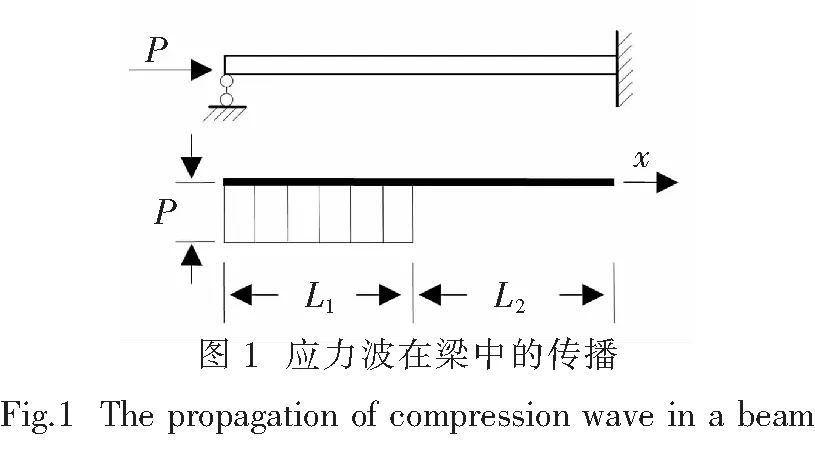
图1中所示加载端简支远端固支欧拉-伯努利等截面梁，长度为L(L=L1+L2)，截面面积为A，截面惯性矩为I，材料密度为ρ，弹性模量为E，横向位移w(x,t).t=0时，在梁加载端作用阶跃荷载P，t时刻应力波的传播距离为L1=ct，c为应力波在梁中的传播速度.

变形能增量为

(1)

动能增量为

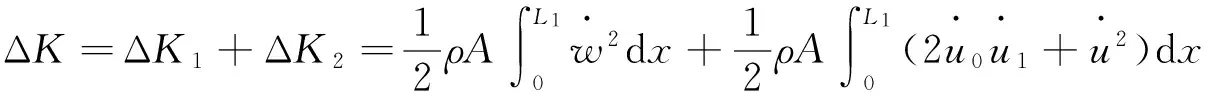
(2)

外力功增量为

ΔW=P·u1(0,t)，

(3)

定义

(4)

由能量守恒定律ΔW=ΔU+ΔK，以及式(4)，有

Upre=Ubuc+ΔK.

(5)

式(5)表示失稳瞬间能量转化过程遵循守恒定律，其中Upre表示失稳时释放出的部分变形能，Ubuc表示新的屈曲变形能.将式(5)对时间t求导，即可得能量转换率守恒条件

(6)

在式(2)中ΔK2相对ΔK1为小量，因而可以忽略ΔK2.将式(2)和式(4)代入临界条件式(5)，采用分离变量式w(x,t)=W(x)·T(t)，并引入无量纲坐标ξ=x/L1，且设

T=C0eωγ(t-t*),

(7)

则可以得到直梁失稳微分控制方程

W(4)(ξ)+λ*W″(ξ)+α*W(ξ)=0,

(9)

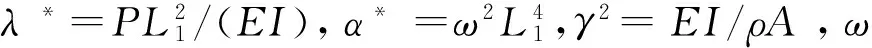
相应边界条件为：

简支端(S)：

W(ξ)=0，W″(ξ)=0.

(10a)

固支端(C)：

W(ξ)=0，W′(ξ)=0.

(10b)

压应力波波前处：

W(ξ)=0，W′(ξ)=0.

(10c)

将式(2)和式(4)代入式(6)，即可得到应力波前附加边界条件

W″(ξ)=0，(ξ=1).

(11)

2 微分求积法(DQM)及其应用

为了对式(9)离散，将积分域等分成n段，共n+1个点,则可以得到有n+5个元素的向量

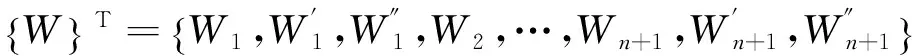
(12)

W表示每个点的位移以及端点的前两阶导数.

设梁的位移函数W(ξ)近似为

(12)

其中[β]为行向量，{f}为Lagrangian坐标列向量.

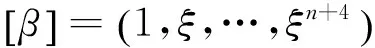
(13)

对式(12)求导，可得

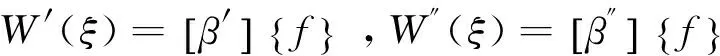
(14)

则有

(15)

采用文献[8-13]中相同的方法，有

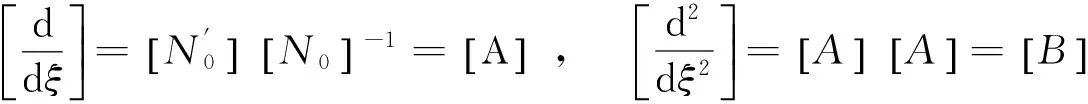
(16)

将控制方程式(9)应用微分求积法，则有

(17)

联立式(17)和边界条件式(10)和式(11)即可得到含临界力参数λ*和动力参数α*的特征方程.

由式(17)和边界条件式(10)和式(11)得到含时间参数的特征方程.逐步增加动力参数α*的值，直到满足附加边界条件(11)式时，即可以得到相应的前三阶动力屈曲临界力参数，且利用式(12)和式(14)即可得到对应屈曲模态和弯矩图.

3 数值算例及讨论

3.1 静力稳定分析

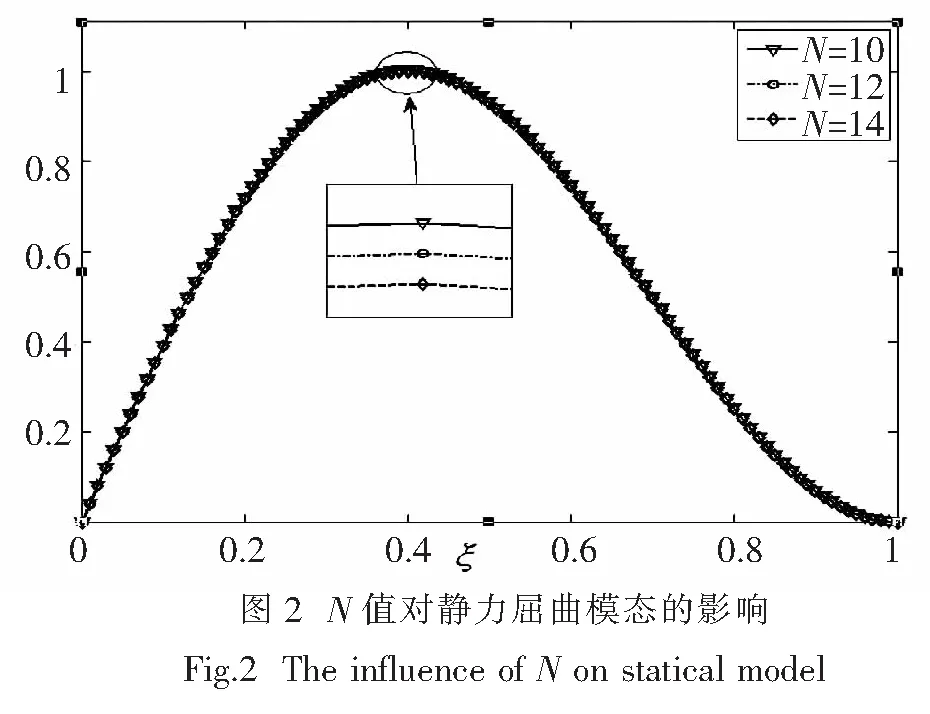
此处先讨论加载端简支远端固支梁的静力屈曲临界力参数，以得到合适的N取值，对动力屈曲进行分析.对于静力失稳，α*=0.利用DQM方法得到加载端简支远端固支梁的静力屈曲临界力参数列于表1，N取不同值时的静力屈曲模态如图2示.

表1 加载端简支远端固支梁静力失稳临界力参数Tab.1 The statical critical buckling loads parameters

从表1可以看出，在N=14时，得到的结果和[14]给出的结果一致.由此可知DQM在求解静力稳定上具有快速收敛和精度高的特点，说明该方法是有效可行的.此外，由图2中可知随着N值的增加，静力屈曲模态幅值变小，更趋近理论解.因此，在接下来的动力稳定分析中取N=14.

3.2 动力稳定分析

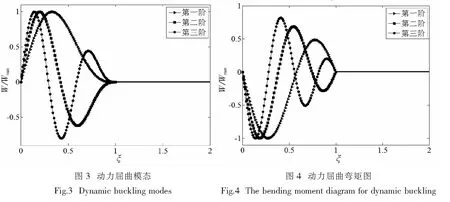
对于动力屈曲，α*>0恒成立.加载端简支远端固支直梁的前三阶动力屈曲临界力参数和动力参数的数值结果列于表2.相应各阶屈曲模态图和弯矩图如图3和图4所示.

表2 应力波在固定端反射前对应的前三阶动力屈曲临界荷载Tab.2 The first three dynamic critical buckling loads before reflection of compression wave

表2表明，在N=14时，本文方法计算得到的动力参数和临界力参数的数值解和[6]中所给结果非常接近，动力参数和临界力参数误差分别小于0.02%和0.03%.相比[15]中利用差分法在N=20时得到的数值结果更加精确，说明本文方法相比差分法更具有收敛速度快和精度高的优点.此外，图3中的屈曲模态和图4中的弯矩图与文献[1]中的结果一致，更进一步验证了该方法的可行性.

3.3 动力与静力比较

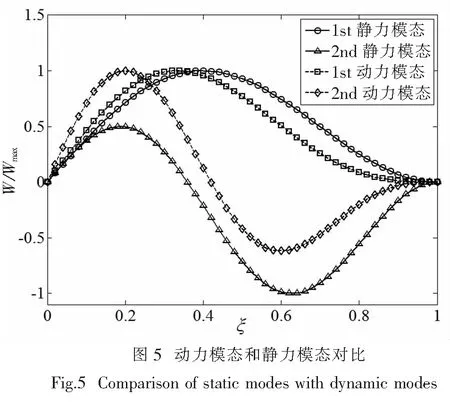
静力屈曲对应动力参数α*=0，应力波下梁动力屈曲对应动力参数α*>0恒成立.为比较两种屈曲形式，考虑等效长度为L1的杆.相应屈曲模态图如图5所示.可见动力屈曲模态和静力屈曲模态有着较大差别.动力屈曲满足应力波前附件边界条件式(11)，即为其有别于静力屈曲的原因.

4 结 论

(1) 利用能量传递和转换守恒推导得到了直梁的屈曲控制方程和压应力波前边界条件.

(2) 利用微分求积法对加载端简支远端固支直梁的静力屈曲和动力屈曲进行了数值分析，并得到了相应临界力参数和动力参数的数值解以及相应屈曲模态图和弯矩图.

(3) 通过与已有文献结果进行对比分析，验证了DQM方法在求解压应力波下直梁动力屈曲问题上的精确性和收敛性.

[1] 王安稳. 弹性压应力波下直杆动力失稳的机理和判据[J]. 力学学报, 2001, 33(6): 812-820.

[2] 韩大伟, 王安稳. 弹性压应力波作用下矩形波板动力屈曲解析解[J]. 工程力学, 2012, 29(11): 12-15.

[3] 韩大伟, 王安稳. 轴向时变冲击载荷作用下直杆弹性动力屈曲研究[J]. 振动与冲击, 2016, 35(5): 181-185.

[4] 毛柳伟, 王安稳. 应力波传播与屈曲耦合情况下结构动力屈曲控制方程及波前边界条件的探讨[J]. 固体力学学报, 2013, 34(4): 152-157.

[5] 毛柳伟, 王安稳, 韩大伟, 等. 考虑应力波效应时直杆塑性动力屈曲研究[J]. 华中科技大学学报(自然科学版), 2012, 40(12): 85-87.

[6] 毛柳伟, 王安稳, 邓磊, 等. 双特征参数法与最优模态法在弹性直杆动力屈曲问题中解的一致性[J]. 工程力学, 2013, 30(1): 87-90.

[7] 毛柳伟, 王安稳, 邓磊, 等. 应力波作用下弹性直杆动力分叉屈曲研究[J]. 振动与冲击, 2014, 33(6): 174-178.

[8] TORNABENE F, FANTUZZI N, BACCIOCCHI M, et al. Free vibrations of composite oval and elliptic cylinders by the generalized differential quadrature method[J]. Thin-Walled Structures, 2015, 97: 114-129.

[9] YUAN Z X, WANG X W. Buckling and post-buckling analysis of extensible beam-columns by using the differential quadrature method[J]. Computers and Mathematics with Applications, 2011, 62(12):4499-4513.

[10] TAHA M, ESSAM M. Stability behavior and free vibration of tapered columns with elastic end restraints using the DQM method[J]. Ain Shams Engineering Journal, 2013, 4(3): 515-521.

[11] DEHGHAN M, BARADARAN G H. Buckling and free vibration analysis of thick rectangular plates resting on elastic foundation using mixed finite element and differential quadrature method[J]. Applied Mathematics and Computation, 2011, 218(6):2772-2784.

[12] YILMAZ Y, GIRGIN Z, EVRAN S. Buckling analyses of axially functionally graded nonuniform columns with elastic restraint using a localized differential quadrature method[J]. Mathematical Problems in Engineering, 2013(2)：1-12.

[13] BEHERA L, CHAKRAVERTY S. Application of differential quadrature method in free vibration analysis of nanobeams based on various nonlocal theories[J]. Computers & Mathematics with Applications, 2015, 69(12):1444-1462.

[14] HUANG Y, LUO Q Z. A simple method to determine the critical buckling loads for axially inhomogeneous beams with elastic restraint[J]. Computers and Mathematics with Applications, 2011, 61(9): 2510-2517

[15] 施连会, 王安稳. 弹性压应力波作用下直杆动力失稳的差分解[J]. 海军工程大学学报, 2007, 19(1): 1-4.

责任编辑：罗 联

The Differential Quadrature Method for Dynamic Buckling of Straight Beam under Elastic Compression Wave

WANGYa-yun,CHENDe-liang*,PENGXu-long,ZHOULu

(School of Civil Engineering and Architecture, Changsha University of Science and Technology, Changsha 410004 China)

Based on the Euler-Bernoulli beam theory and the principle of conservation of energy, the buckling governing equation and the boundary conditions at the compression stress wave front for a uniform beam are established. Then, the dynamic buckling of uniform straight beam under coupled stress wave propagating and dynamic buckling before reflection of compression wave is investigated. And the eigen-equation is obtained with the differential quadrature method(DQM) and the boundary conditions by transferring governing equation into the linear algebraic equation sets. Moreover, a numerical investigation for dynamic buckling of the beam simply supported at loaded end and clamped at other end is carried out. The results shows that the present method has good accuracy and convergence.

straight uniform cross-section ; compression wave; the differential quadrature method; dynamic buckling

2016-05-20

国家自然科学基金项目(11172051，11202038);湖南省自然科学基金项目(2015JJ4006，2016JJ3002)；长沙理工大学研究生科研创新项目(CX2016SS02)

陈得良(1971-)，男，湖北 英山人，博士，教授.E-mail:deliang_chen@126.com

O347

A

1000-5900(2016)03-0030-05