地铁车站导洞双向开挖对地层沉降影响研究*

李 涛， 王 帅， 陈慧娴， 刘 波， 王珑桦

(中国矿业大学(北京) 力学与建筑工程学院，北京 100083)



地铁车站导洞双向开挖对地层沉降影响研究*

李 涛*， 王 帅， 陈慧娴， 刘 波， 王珑桦

(中国矿业大学(北京) 力学与建筑工程学院，北京 100083)

地铁车站洞桩法导洞的开挖过程、方向及顺序是控制地层沉降的关键.基于北京某地铁车站施工过程中地层沉降的实测数据，建立三维有限差分数值模型，详细分析导洞双向开挖时地层的沉降规律；在此基础上，进一步分析了上覆土层厚度、洞径、洞距对地层沉降曲线中反弯点距离i的影响.结果表明：导洞开挖结束后地表沉降便随即趋于稳定，基本无滞后性；地层沉降主要在车站中心线左右30 m范围内；横通道中心线反弯点距离i约为2.5倍洞距，其与洞径是近似线性的反比例关系，其与导洞埋深是近似线性的正比例关系.研究结果对类似工程建设具有参考意义.

地铁车站；洞桩法；数值模拟；地表沉降；沉降槽

近年来，洞桩施工法普遍用于北京地铁车站的建设中.然而，城市地铁车站施工区域一般人口密集、场地较小、交通繁忙、地下管线网复杂，如何准确控制地层沉降便是洞桩法施工的关键问题.

国内外已有许多学者针对上述问题做了研究，并取得了一些成果：[1]在研究巷道的地表沉降时就首次提出了隧道开挖引起的横向地表沉降槽符合高斯分布.[2]提出了地层损失的概念和预测隧道开挖引起地表沉降的使用方法，即Peck公式.[3-5]研究三维弹塑性有限元方法，总结出了三维弹塑性本构模型，使用三维弹塑性有限元分析计算开挖产生的位移，并且对盾构施工过程中的地层损失进行了模拟.[6]基于上海地区特殊的地质条件和施工工况，对Peck公式进行了修正，得到了候学渊公式.[7]通过模型试验得出地表沉降的范围与洞径的关系，即沉降范围约为4倍洞径.另外，有些学者根据不同的理论，进行了数值模拟分析[8-16]，说明导洞开挖阶段引起的地表沉降对地铁车站施工地表沉降的影响最大.

然而，目前大多研究都缺乏充足的现场监测数据，使得理论研究与实际不太相符.基于此，本文以北京地铁7号线达官营车站洞桩法施工为背景，结合现场监测数据，采用FLAC3D数值软件对该车站临时竖井横通道处双向导洞施工进行模拟分析，并与现场数据进行对比，详细分析导洞双向开挖时地层的沉降规律，在此基础上，进一步分析了上覆土层厚度、洞径、洞距对地层沉降曲线中反弯点距离i的影响，为实际施工提供科学合理的依据.

1 工程概况

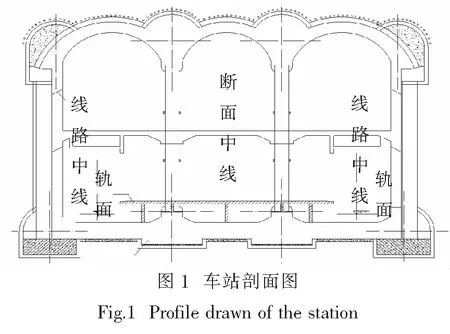
北京地铁某车站采用洞桩法施工.车站中心里程顶板覆土厚度9.17 m，车站为地下二层三跨岛式站台车站(如图1)，地下一层为站厅层，地下二层为站台层.施工的顺序:先开挖上下8个导洞，在上层导洞向下施做围护桩及拱顶，之后开挖上层站厅并施做中板，最后开挖下层站台并施做底板，完成.

施工场地地表以下为潜水，河卵石层、中粗砂1层为主要含水层，这两个岩层透水性好，水位一般为17.15～18.47 m (水位埋深26.40～27.50 m).含水层的地下水分布连续，岩层渗透系数大，为强透水层.水量补给主要来自侧向径流、越流及“天窗”渗漏，排泄方式主要以地下径流为主.该层水的年内动态与大气降水关系密切.由于施工结构位于含水层，应采取降水措施，将水位控制在结构底部1 m以下，确保无水施工.

2 洞桩法数值模拟分析

2.1 模型描述

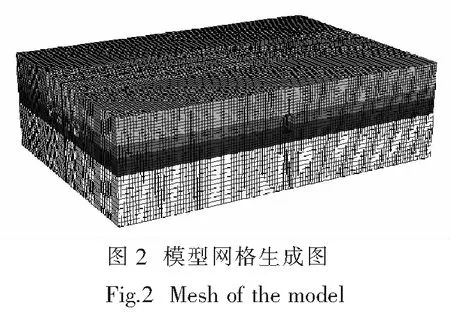
2.1.1 尺寸 根据设计条件，范围确定为：沿车站纵向总长126.5 m，沿车站横向总长88.2 m，高度36 m，单元总数343 012.模拟地层分为4层，即人工填土层、卵石层1、卵石层2和强风化砾岩、泥岩层.三维计算模型网格如图2所示.

2.1.2 荷载 模拟过程考虑地层压力：垂直方向为上覆土层的重度，水平方向为垂直地压乘以侧土压力系数(取0.43).

2.1.3 边界条件 模型上表面为地表，取自由边界；底面和侧面为位移边界，均施加法向约束.

2.1.4 本构模型、变形模式、参数选取 岩土体采用摩尔-库伦准则，柱桩拱等支撑采用弹性体模型.变形采用大应变变形，开挖每步按1 m施工进度推进.注浆采用加强拱部材料参数来实现.开挖是采用null命令模拟，支护用的格栅钢架采用shell单元模拟.数值模拟的各项参数(包括地层参数、支护参数)详见表1、表2.

表1 土层物理力学性质Tab.1 Soils parameters

表2 支护结构参数Tab.2 The parameters of support structures

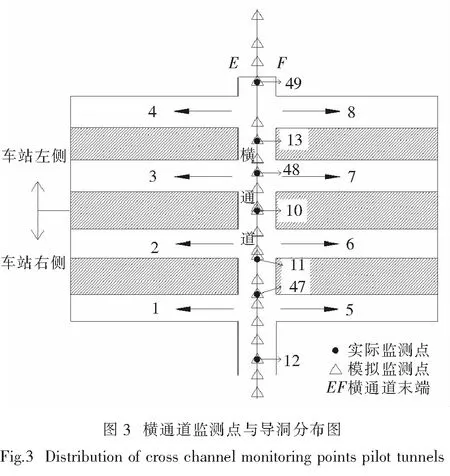
2.1.5 监测点的设置 本次模拟计算设置了多个监测点，这些监测点由两部分组成：实际工程中使用的监测点和数值模拟中添加的监测点，如图3所示，圆形和三角形分别为实际监测点和模拟监测点.这样能在后续数据处理分析中，更好地将模拟结果与实测结果进行对比.本文重点分析了横通道中心线上各监测点的沉降规律.

2.2 开挖方案

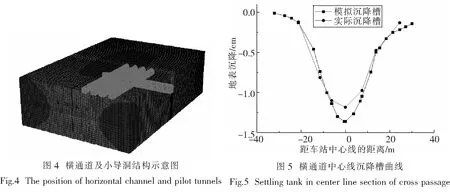
模拟开挖时(如图4)，先开挖横通道，横通道完成后开始开挖小导洞，小导洞双向均开挖至30 m，模拟结束.开挖方案为1，4—2,5,8—3,6—7.实际施工中(如图3)，首先开挖1号和4号导洞(向西)，待1号和4号导洞施工至15 m时，同步开挖2号导洞(向西)、5号和8号导洞(向东)，同样，待2、5、8号三个导洞施工15 m后，继续开挖3号(向西)和6号导洞(向东)，最后等到3号和6号导洞施工至15 m时，同步开挖7号导洞，每次开洞的错开距离为15 m.

2.3 计算与实测结果分析

2.3.1 横通道中心线的地表沉降分析 由图5中变化趋势可以看出，在距车站中心线左右各20 m范围内，地表沉降的现场实测值和数值模拟值是基本吻合的.另，由数值计算结果可知导洞开挖引起的沉降影响范围为车站中心线左右各30 m.右侧沉降区域较左侧略大，原因在于横通道的开挖只到达了点E和F处，横通道末端EF与边导洞4和8的距离是1 m，而横通道端头钢格栅具有加固作用，因此沉降并不是以车站中心线为对称轴的规则图形.在车站中心线左右20 m的范围内，越靠近车站中心的监测点沉降值越大，且最大分别为模拟值-1.36 cm和实际值-1.18 cm.模拟最大沉降值大于实际的最大沉降值，原因在于本次数值模拟的过程仅考虑了土体在荷载及自重情况下开挖产生的位移，而实际工程中，还采取了分层分布开挖、复杂的超前注浆等一系列措施来控制地表的沉降，这些措施在模拟中不能完全再现，而它们对控制变形起到了积极的作用，故数值模拟的结果比实测的结果略大，在复杂的大型工程中留有一定的安全储备也是有必要的.各项支护参数详见表2.

2.3.2 实际地表沉降槽拟合曲线和模拟地表沉降槽拟合分析 依据Peck公式，利用数据分析软件，对实际监测点数据和模拟监测点数据分别进行拟合分析，得到了横通道中心线横截面上的实际地表沉降槽拟合曲线和模拟地表沉降槽拟合曲线(如图6所示).拟合公式[2]如下：

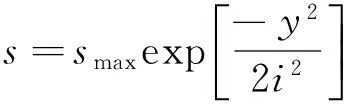
(1)

式中，s为地表任意一点的沉降值；smax为地表沉降最大值，位于沉降曲线的对称中心线上(对应于横通道轴线位置)；y为从沉降曲线中心到所计算点的距离；i为从沉降曲线对称中心到曲线反弯点的距离.

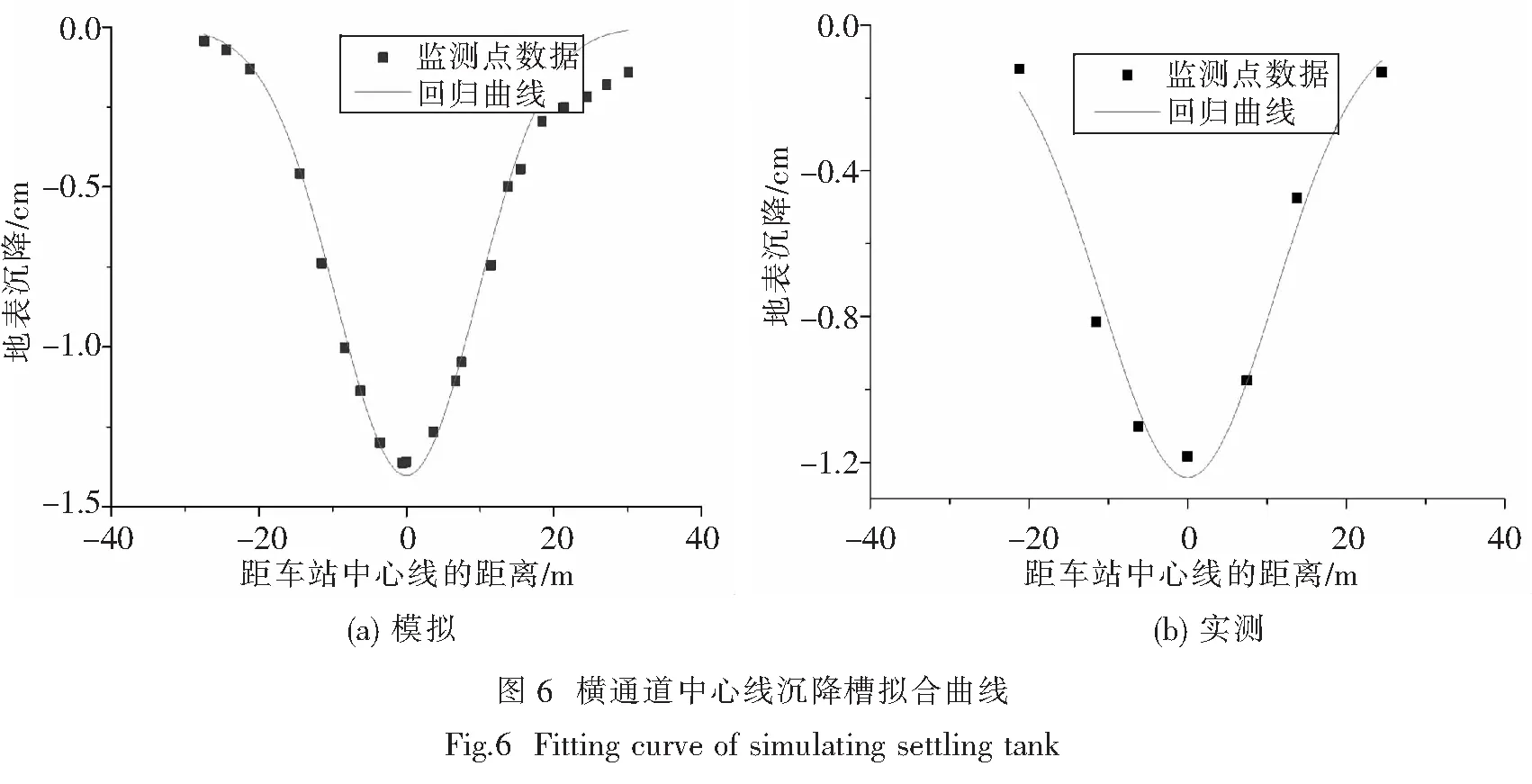
由图6(a)、(b)的变化趋势可以看出，实际沉降槽和模拟沉降槽都是符合Peck曲线分布规律的.实际沉降槽拟合曲线反弯距点i为11.79 m，smax为-1.24 cm；模拟沉降槽拟合曲线i为9.09 m，smax为-1.40 cm.两者i相差2.70 m，smax相差0.16 cm.由于地层非水平均质，注浆情况未完全考虑浆液强度的变化，以及施工中受周围临时附加荷载的影响等，造成实测数据与数值计算结果之间存在一定偏差，而这种偏差都在工程安全控制范围内，且它们表现出规律的一致性.

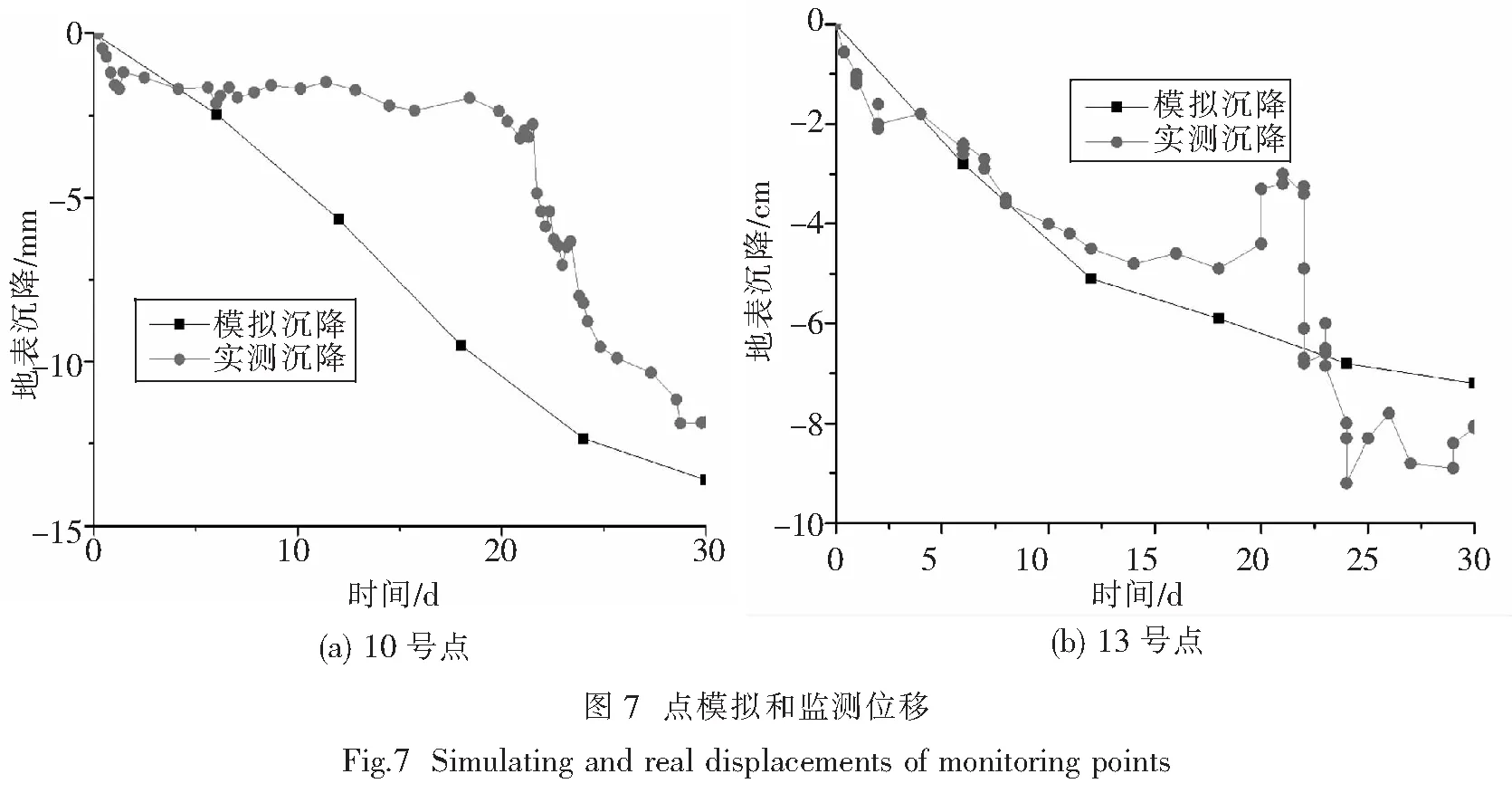
2.3.3 单点沉降分析 选取10号和13号两个监测点进行单个点的沉降分析.由图7(a)和(b)中的变化趋势可以看出，10号和13号监测点最终的模拟和实测沉降值都比较接近.10号监测点的模拟沉降曲线与实际沉降曲线变化趋势大体上是相同的，与13号监测点的变化趋势基本一致.10号点模拟沉降值略大于实测沉降值，这是由于数值模拟未能完全考虑注浆量、注浆压力以及施工荷载等因素对地层位移的影响.13号点模拟沉降呈现平缓下降变化，而实际沉降曲线出现或高或低的波动段，原因在于数值模拟考虑的是按顺序开挖的过程，而实际施工过程要复杂得多， 如施工的1～20 d内开挖至近13号点下方处，施工过程顺利，该过程变化趋势是相对平缓的，最大沉降-5.9 mm；随着开挖深入，距离13号点越来越近，该点受到的扰动在慢慢变大，沉降亦随之增加；20～22 d曲线向上波动，最小沉降-3 mm，这是由于注浆量过大导致该点隆起，现场注浆时注浆量和注浆压力较难控制；22～24 d曲线出现了陡降现象，最大沉降-9.2 mm，这是由于开挖使土体受到扰动过大，出现了一定量的塌方现象；25～30 d曲线上下波动随后趋近平稳，这是塌方被控制后，随着继续开挖距离该点越来越远，该点受到的扰动逐渐变小，最终沉降趋近于稳定.

2.3.4 各个施工节点横通道中心线地表沉降分析 依据实际开挖顺序，分别研究5个施工节点对横通道中心线地表沉降，绘制出了各施工节点的横通道中心线地表模拟沉降槽曲线.

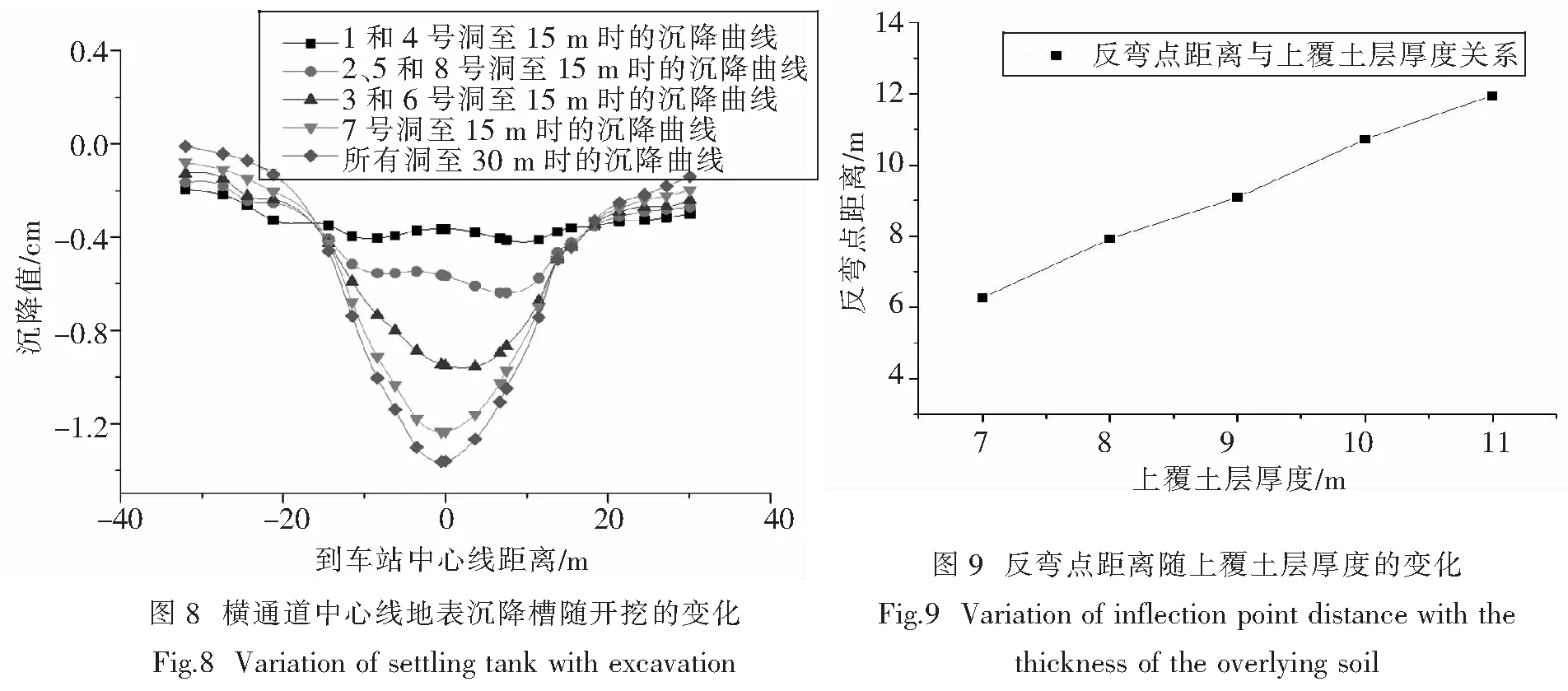
如图8所示，当导洞1和4开挖到15 m后，横通道中心线地表迅速下沉，且两侧沉降较大，最大沉降值为0.41 cm，这主要是由于边导洞1和4离车站中心较远.当导洞2、5和8开挖到15 m后，地表右侧沉降迅速加大，最大沉降值达到0.64 cm，这是由于车站右侧施工的导洞多于左侧，对地表沉降的影响大于左侧；当中导洞3和6开挖到15 m后，车站中心的沉降迅速加快，右侧开挖的导洞仍然多于左侧，因此右侧的沉降仍大于左侧，最大沉降值达到0.64 cm；当导洞7开挖到15 m后，左侧的沉降也迅速加快，中心处的地表沉降继续快速加大，最大沉降值为1.24 cm；最后，当所有导洞全开挖至30 m后，地表沉降快速完成，最大沉降值为-1.36 cm.由此可见，每一步节点完成后，沉降迅速完成.故横通道中心地表沉降随施工节点的进行，基本无滞后性.

3 地层沉降范围的影响因素研究

采用FLAC3D对地铁车站导洞施工进行模拟，探讨上覆土层厚度、导洞洞径、洞距3个因素对地层沉降曲线中反弯点距离i的影响，进而分析这3种因素对地表沉降范围的影响.

3.1 模型及计算参数

为使研究更具有突出性，各模型均选取同样的土层参数(表1)、支护参数(表2)和开挖方案(图3).在2.1节的基础上对模型进行了如下改进：在其他所有条件不变的前提下，改变上覆土层厚度，分别得到上覆土层厚为7、8、9、10、11 m的模型；在其他所有条件不变的前提下，改变导洞开挖时的洞径和洞距，得到洞径分别为3、3.5、4、4.5、5 m，洞距分别为2.85、3.35、3.85、4.35、4.85 m的模型.

3.2 计算结果及分析

3.2.1 上覆土层厚度的影响 上覆土层厚度分别取7、8、9、10、11 m，模拟得到反弯点距离与上覆土层厚度的关系曲线，如图9所示.

从图9可看出：上覆土层厚度对反弯点距离的影响是显著的.当上覆土层厚度为7、8、9、10、11 m时，反弯点距离分别为6.27、7.93、9.09、10.72、11.95 m.随上覆土层厚度的增加，反弯点距离逐渐增大，且变化趋势近似为线性.

由此可见：在一定范围内，反弯点距离与上覆土层厚度是近似线性的正比例关系.

3.2.2 洞径和洞距的影响 导洞洞径分别取3、3.5、4、4.5、5 m，洞距分别取2.85、3.35、3.85、4.35、4.85 m，模拟计算得到反弯点距离与不同洞径及洞距的关系曲线，如图10所示.

从图10可看出：导洞洞径及洞距的改变对反弯点距离的影响都是明显的；随着洞径的增加，反弯点距离明显增大，当导洞洞径为3、3.5、4、4.5、5 m时，反弯点距离分别为10.66、9.89、9.09、8.31、7.66 m；随着洞距的增加，反弯点距离明显减小，当洞距为2.85、3.35、3.85、4.35、4.85 m时，反弯点距离分别为7.66、8.31、9.09、9.89、10.66 m.

由此可见：反弯点距离与导洞洞径是近似线性的反比例关系，反弯点距离与导洞洞距是近似线性的正比例关系，且反弯点距离约为2.5倍洞距.

4 结 论

(1) 导洞施工阶段是引起地表沉降的主要阶段，施工引起的地表沉降变形曲线与Peck公式预测曲线基本一致，导洞施工阶段的地表沉降与导洞群的施工密切相关，沉降基本无滞后性.

(2) 模拟结果表明，横通道中心线的反弯点距离与导洞的埋深、洞径和洞距等因素存在关系.反弯点距离与埋深和洞距皆是近似线性的正比例关系，且反弯点距离约为2.5倍洞距.反弯点距离与洞径是近似线性的反比例关系.

(3) 本次数值模拟的结果符合实际施工的情况，该数值模拟所用的模型及参数较好地与实际情况相符合，因此该模型可以推广用于类似的施工方案.

[1] MARTOS F. Concerning an approximate equation of subsidence through and its time factors[C]. Proc of the International Strata Control Congress.Leipzig,1958.

[2] PECK R B. Deep excavation and tunneling in soft ground[C].Proc 7th Int Conf on Soil Mechanics and Foundation Engineering.Mexico City,1969: 225-290.

[3] LEE K M, ROWE R K. Finite element modeling of the three-dimensional ground deformations due to tunneling in soft cohesive soils : part I——Method of analysis[J]. Computers and Geotechnics,1990,10:87-109.

[4] LEE K M, ROWE R K. Finite element modeling of the three-dimensional ground deformations due to tunneling in soft cohesive soils: part II——Method of analysis[J].Computers and Geotechnics, 1990,10:111-138.

[5] LEE K M, ROWE R K. An analysis of the three-dimensional ground movement: the Thunder Bay tunnel[J].Canadian Geotechnical Journal,1991,28(1):25-41.

[6] 刘建航,候学渊. 盾构法隧道[M].北京：中国铁道出版社,1991.

[7] 周顺华. 地下铁道车站和开挖环境模拟[D].成都：西南交通大学,1996.

[8] 易宏伟,孙钧. 盾构施工对软粘土的扰动机理分析[J]. 同济大学学报,1999,28(3):277-281.

[9] 高成雷, 罗书学, 朱永全. 浅埋暗挖洞桩法的三维有限元模拟分析[J].石家庄铁道学院学报,2002,15(3):44-47.

[10] 陶龙光, 刘波, 丁城刚. 盾构过地铁站施工对地表沉降影响的数值模拟[J].中国矿业大学学报，2003,32(3):236-240.

[11] 李铀, 李小强, 彭意. 地铁施工中的地表沉陷控制方法与工程实例[J].岩石力学与工程学报,2004,23:5111-5117.

[12] 李晓霖. 地铁车站洞柱法的数值模拟研究[J]. 地下空间与工程学报,2007,3(5):928-932.

[13] 俞缙, 许琼鹤, 邢葳葳. 基坑工程地铁隧道隆起位移数值模拟分析[J].岩土力学,2007,28:653-657.

[14] 瞿万波, 刘新荣, 傅晏. 洞桩法大断面群洞交叉隧道初衬数值模拟[J]. 岩土力学, 2009,30(9):2799-2804.

[15] 姚君华, 宋文杰, 董军. 洞柱法导洞不同开挖顺序对地表沉降的影响[J].公路学报,2013(1):298-301.

[16] 宋战平, 张丹锋, 曲建生. 承压水砂土地层桩洞法施工变形控制研究[J].西安建筑科技大学学报,2015, 47(1):33-38.

责任编辑：罗 联

A Research of Two-way Heading Excavation of Subway Station on the Surface Subsidence

LITao*,WANGShuai,CHENHui-xian,LIUBo,WANGLong-hua

(School of Mechanics and Civil Engineering, China University of Mining and Technology(Beijing), Beijing 100083 China)

The pilot tunnel excavation process, the direction and the sequence of subway station hole pile method are keys to control strata subsidence. Based on the measured data of surface subsidence in the process of Beijing metro station construction, the 3 d finite difference numerical model is established and the subsidence regularity of two-way heading excavation is analyzed minutely. On this basis, the influences of the overburden thickness,hole diameter and hole spacing on the strata subsidence curve inflection point distanceiare further analyzed. Results show that, after the pilot tunnel excavation the surface subsidence is stable immediately and nearly has no lag. Surface subsidence is mainly located in the area within the range of 30 meters to the center line of the station. Theiis about 2.5 times of hole spacing. The relationship between hole spacing andiis proportional and linear. The relationship between overburden thickness andiis also proportional and linear. The results of the study have reference and significance for similar engineering construction.

subway station; hole pile method; numerical simulation; surface subsidence; settling tank

2016-03-05

国家自然科学基金青年科学基金项目(51508556)；北京高等学校青年英才计划项目(YETP0944)；中央高校基本科研业务费专项资金项目(2009QL02)

李涛(1981-)，男，河南 新郑人，博士，副教授，硕士生导师. E-mail:litaocumtb@163.com

U231.3

A

1000-5900(2016)03-0023-07