不能这样“巧用对称求最值”

北京丰台二中

甘志国 (邮编：100071)



不能这样“巧用对称求最值”

北京丰台二中

甘志国 (邮编：100071)

我们先看发表的文章《巧用对称求最值》[1]的主要内容：

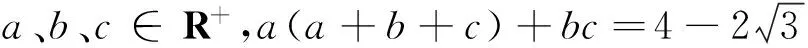
解 由已知b、c位置对称，可知当2a+b+c取最小值时，b=c成立，此时

a(a+b+c)+bc=a2+2ab+b2

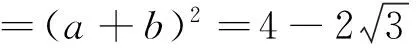
题2 (1989年苏联奥林匹克数学竞赛题)若x、y、z∈R+,xyz(x+y+z)=1,求(x+y)(y+z)的最小值.

解 由已知x、z对称可得，当(x+y)(y+z)取最小值时，x=z,所以题设变为

1=xyz(x+y+z)=x2(2xy+y2)

(x+y)(y+z)=(x+y)2≥2，

解 由式子结构知，x1、x2位置对称，当取得最小值时，x1=x2成立.

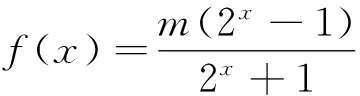
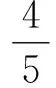
题4 若二次函数f(x)=ax2+bx+c的值域为[0,+),求的最小值.

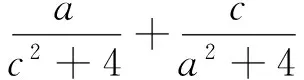
也有文献资料用“对称原理”来编拟关于不等式的习题：在△ABC中，我们欲求sinA+sinB+sinC的最值.

反例2 设x、y∈R,x+y=2,求x+y的最值.

易知x+y的最大值、最小值均是2，但并不一定是在x=y时取到.

反例3 (《数学通报》2010年第4期数学问题1844)已知a、b、c为正实数，且a+b+c=12,ab+bc+ca=45,求abc的最大值.

答案 当且仅当a、b、c中有两个取3，另一个取6时，abc取到最大值，且最大值是54(但此最大值并不是在a=b=c时取到).

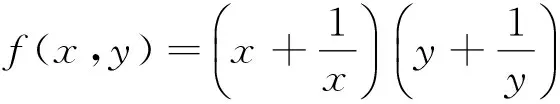
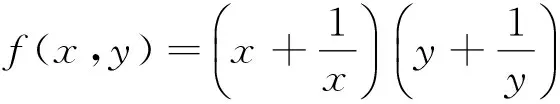
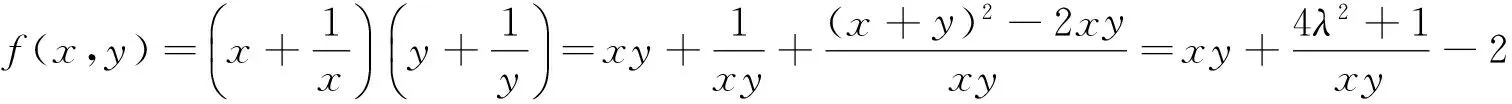
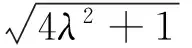
反例7 设x、y∈R,x+y=20,求f(x,y)=xy(x4+y4)的最值.

下面再来研究反例7的一般情形：设x、y∈R,x+y=2λ(λ是正常数)，求f(x,y)=xy(x4+y4)的最大值.

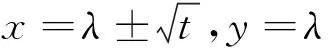
f(x,y)=g(t)=…=-2(t3+5λ2t2-5λ4t-λ6)(t≥0)，

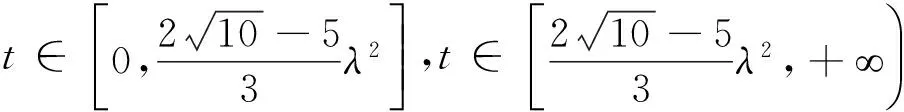
反例8 (2016年高考江苏卷第14题)在锐角三角形ABC中，若sinA=2sinBsinC,则tanAtanBtanC的最小值是______．

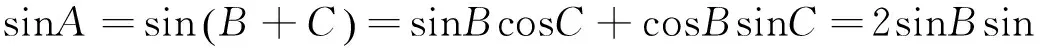
又三角形ABC为锐角三角形，得cosB>0,cosC>0，

所以tanB+tanC=2tanBtanC．

所以

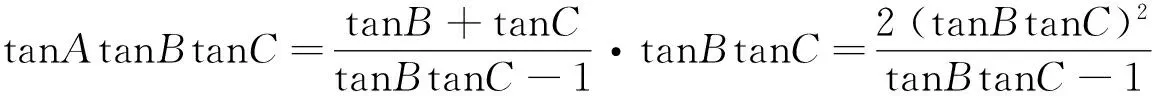
再设t=tanBtanC-1(t>0),得

注 本题是关于B、C对称的，但所求的最小值并不是在B=C时取到的.

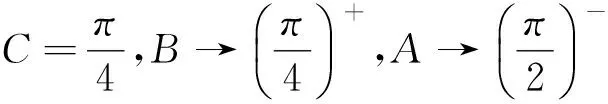
下面再来给出文献[1]中四道例题的正确解答.

题1的解答 由题设，可得

题2的解答 由题设，可得

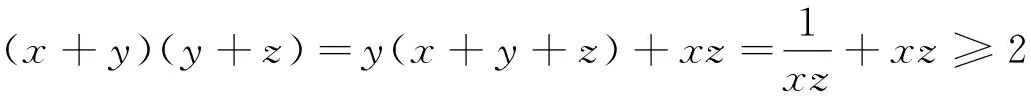
当且仅当x,y∈R+,xz=y(x+y+z)=1时，(x+y)(y+z)取到最小值且最小值是2.

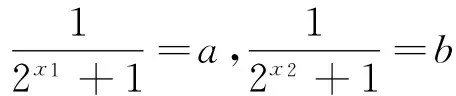
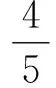
题4的解答 在原解答中已得题设即“a>0,c>0,ac=4”，所以a+c≥4.

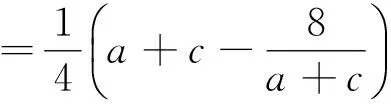
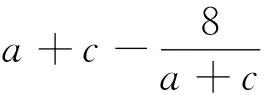
1 高丰平.巧用对称求最值[J].数理天地(高中版)，2013(3)：6

2 甘志国著.初等数学研究(II)下[M].哈尔滨：哈尔滨工业大学出版社，2009：389-390

3 甘志国.也谈一道三角题的解答[J].中学数学教学，2011(2)：41-42

2016-08-25)