由一道竞赛题引发的思考

山东省高青县教学研究室

董 林 (邮编：256300)

山东省高青县第一中学

赵桂霞 (邮编：256300)



由一道竞赛题引发的思考

山东省高青县教学研究室

董 林 (邮编：256300)

山东省高青县第一中学

赵桂霞 (邮编：256300)

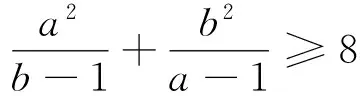
这是一道第26届独联体数学奥林匹克试题.本题看似结构简单，但却蕴含着丰富的资源和信息，本文将围绕这个题目展开思考，借以探讨数学问题研究的角度和维度.

1 考虑问题的解决方法

对于分式不等式，最常规的证明方法是去分母，但作为竞赛题的解决，这个思路一般是不胜其烦或难于奏效.

竞赛中的分式型不等式问题的证明，常用的是代换法，代换一般采用分母整体代换、增量代换和三角代换的方法.

证法1 (分母整体代换)

设x=a-1，y=b-1，已知a>1，b>1，所以x>0，y>0.根据基本不等式有

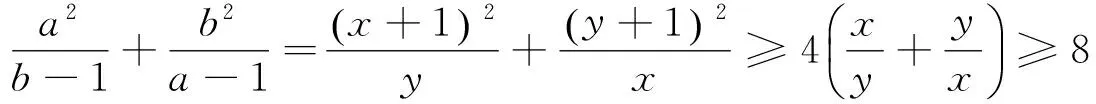
证法2 (增量代换)

已知a>1，b>1，设a=1+x，b=1+y，以下同证法1，从略.

证法3 (三角代换)

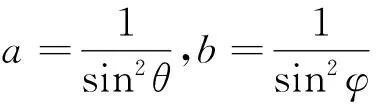
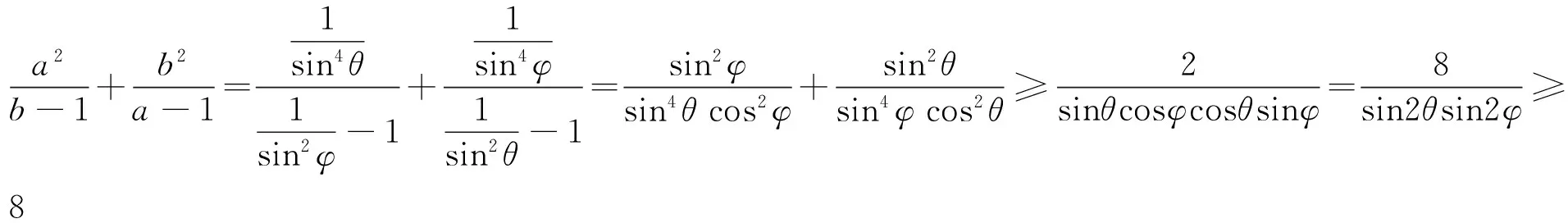
竞赛中的分式型不等式的证明，还常常借助于一些现成的结论，如排序不等式、Cauchy不等式，等等.

证法4 (利用排序不等式)

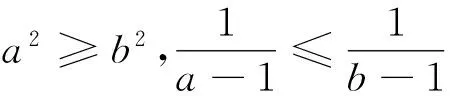
证法5 (利用Cauchy不等式)

已知a>1，b>1，所以a-1+b-1>0，利用Cauchy不等式知

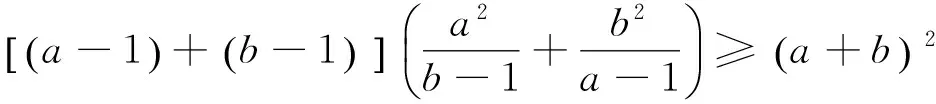
所以有

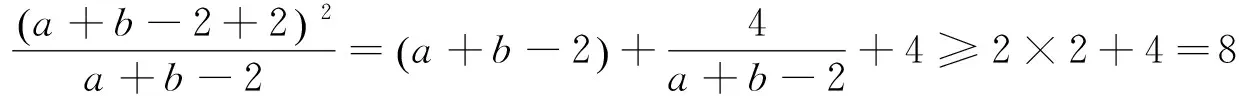
另外，通过配凑“处理掉”不等式中的分母，也是时常思考的解决问题的角度之一.

证法6 (配凑法)

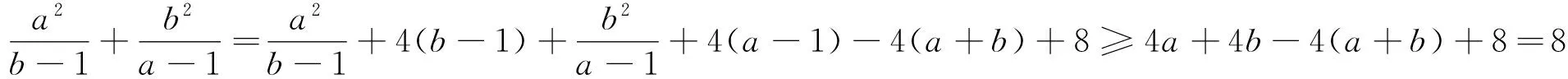
从代换、去分母、运用基本不等式等多方面思考还会找到其他的证明方法，读者不妨一试.

2 推广

考虑问题的推广，我们往往从维数和次数两个角度进行探索.

2.1 维数的推广

从对原问题的证明过程中我们可以看到，原问题中的不等式等价于下面的不等式：

命题1 若x、y是正数，则有

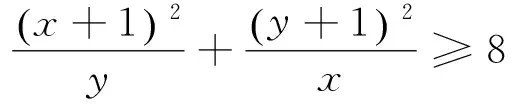
对于这个问题，最为简洁的证法是上述证法中的证法1.

顺着这个思路，我们可以得到

命题2 若x、y、z是正数，则有

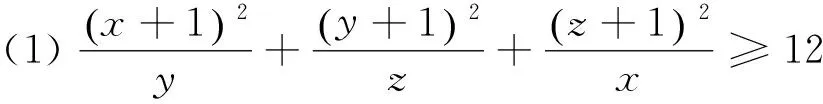
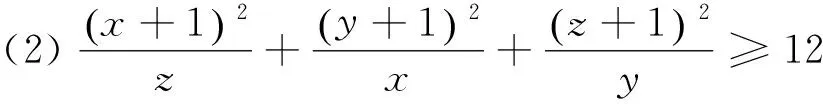
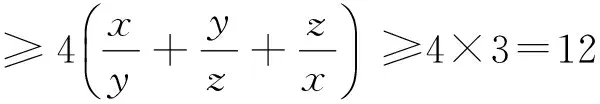
(2)的证明与(1)相似，在此从略.

将命题2中的两个不等式还原成原来的形式就是如下两个不等式：

命题3 若a>1，b>1，c>1，则有

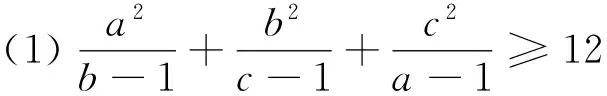
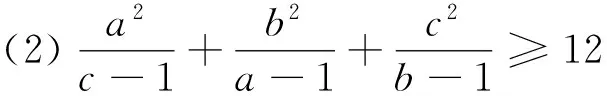
读者可以探究上述命题的其它解法，继续顺着这个思路，我们可以进一步得到

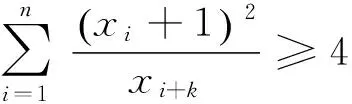
(注：当i+k>n时，取xi+k=xi+k-n)

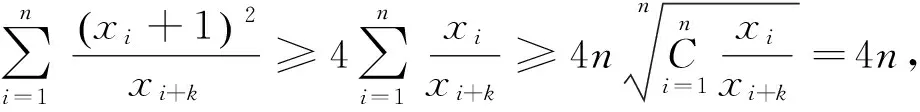
2.2 次数的推广

考虑将分式中分子的次数进行推广，我们可以得到

命题5 若x、y是正数，n是整数且n≥2，则有

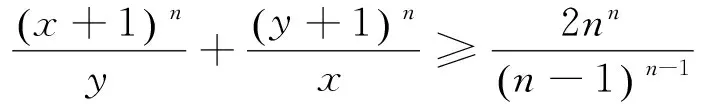
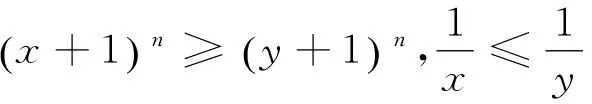
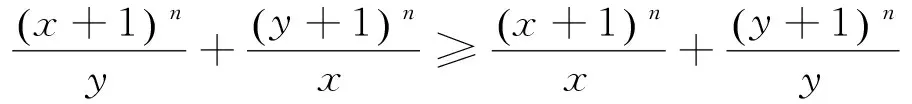
已知n是整数且n≥2，考察函数

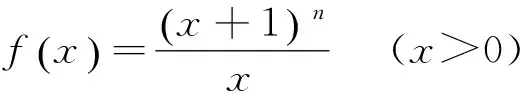
对其求导数，有

显然有

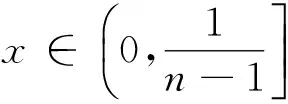
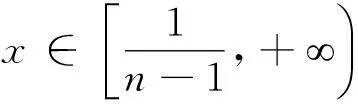
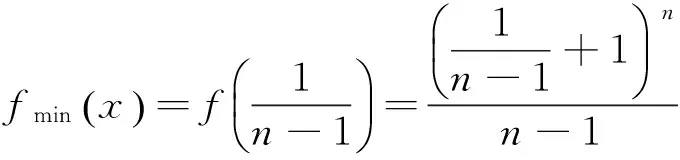
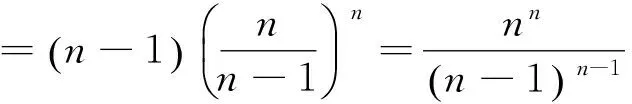
从而有

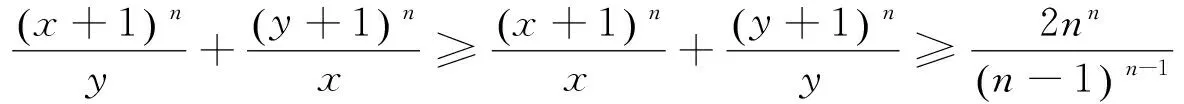
有兴趣的读者，不妨将维数、次数的推广结合考虑，会得出更多漂亮的结果.

3 加强

在不等式问题的研究中，我们还通常考虑对其进行加强，得到更强的结果，比如对于命题1，我们可以得到

命题6 若x、y是正数，则有

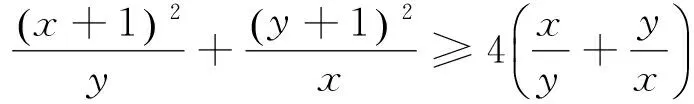
将命题6的结果还原成原来的形式就是

命题7 对任意实数a>1、b>1，有

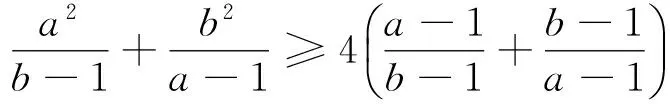
经探索，我们还会得到如下结果

命题8 对任意实数a>1、b>1，有

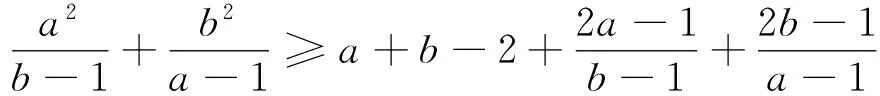
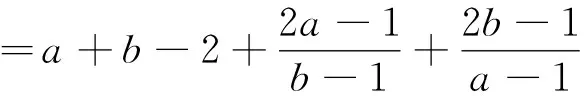
下面说明命题8也是原不等式的一个加强：

只要说明

根据命题8的证明可知

≥2+2+2×2=8.

所以命题8的结论强于原问题.

读者可顺着这样的思路考虑对我们推广了的结论进行加强.

对不等式问题，从寻求多种证法、对结论进行推广和加强等角度进行探究，除了能发现许多有价值的、漂亮的结论外，更重要的是能够培养良好的数学思维能力，优化思维品质，有兴趣的读者不妨找一些不等式结论进行探究，相信一定会收到意外的惊喜！

2016-08-26)