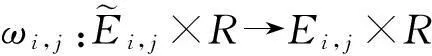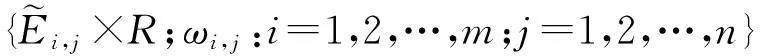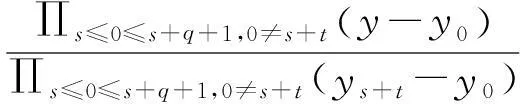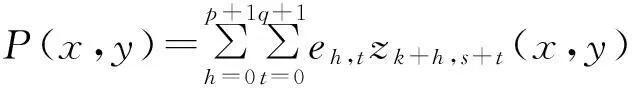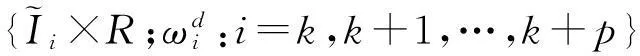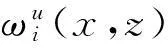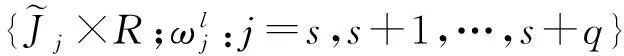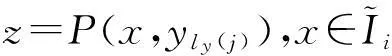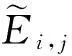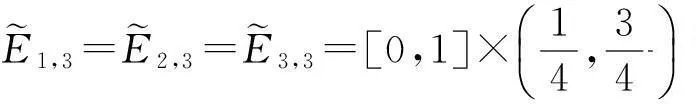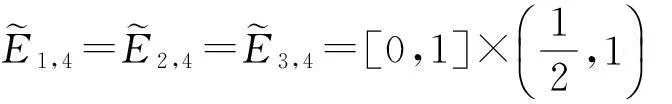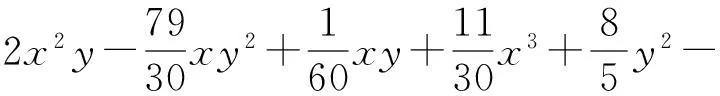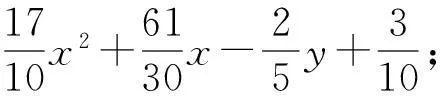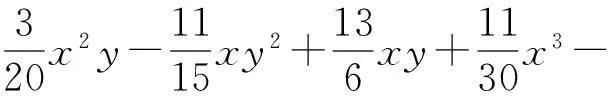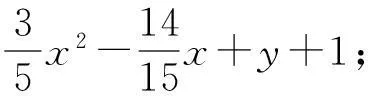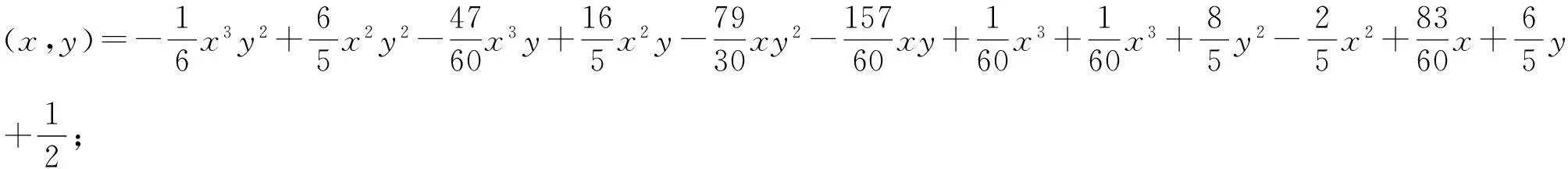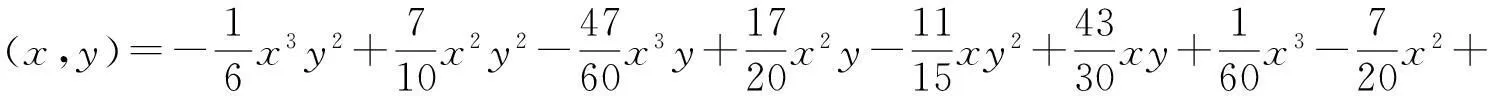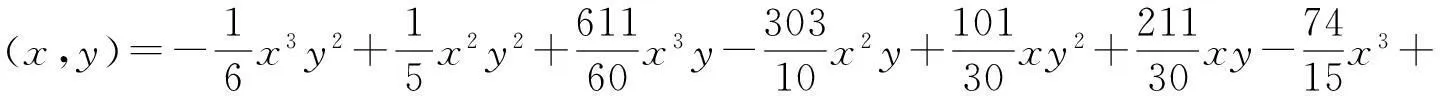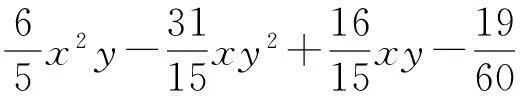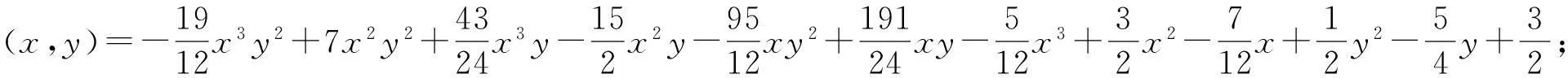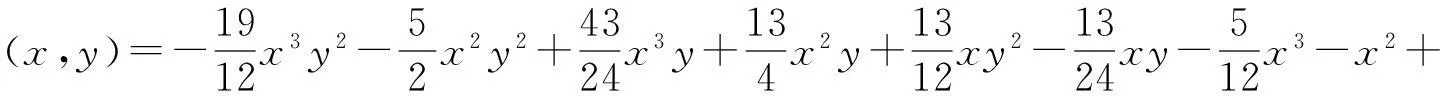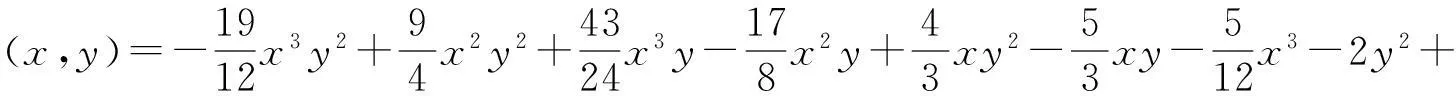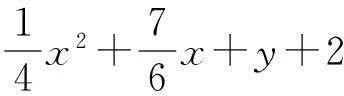基于多项式的递归分形插值曲面的构造

康　云， 冯志刚*， 郭艳芳

(1 江苏大学 理学院，江苏 镇江 212013； 2 山西应用科技学院， 山西 太原 030062)



基于多项式的递归分形插值曲面的构造

康云1， 冯志刚1*， 郭艳芳2

(1 江苏大学 理学院，江苏 镇江 212013； 2 山西应用科技学院， 山西 太原 030062)

摘要：为了利用多项式构造递归分形插值曲面，根据分形插值方法给定的插值节点, 可以构造适当的迭代函数系(IFS), 使得迭代函数系的不变集是一个连续插值函数的图像。根据这个多项式, 构造含有常数尺度因子的迭代函数系, 证明该迭代函数系的不变集就是过插值节点的分形插值曲面。通过改变分形纵向尺度因子的大小可以调节分形插值曲面的粗糙程度。

关键词:递归迭代函数系；分形插值曲面；二元连续多项式；不变集

MR subject classification: 03C40

分形插值函数是拟合数据的一个常用方法，在函数逼近、数值分析研究以及数据拟合应用中都占有重要地位,受到相关学者的广泛关注。它既为函数逼近论开辟了新的研究领域，又为计算机图形学提供了有力的工具，还广泛用于冶金学、地质学、化学、医药科学等领域。

20世纪80年代，美国数学家Barnsley[1-2]首先提出了分形插值方法, 根据给定的插值节点, 可以构造适当的迭代函数系(IFS), 并且说明了迭代函数系的不变集就是一个插值函数的图像。可以通过选择迭代函数系的某些参数(称为纵向压缩因子)，使得这个插值函数具有理想的粗糙程度。 基于Barnsley分形插值的思想，文献[3]提出了三角区域上分形插值曲面的构造方法。为了保证得到的分形插值曲面的连续性，附加了边界上插值节点共面的条件。 但Massopust的构造方法仍然存在一些问题，就是缺少自由压缩因子和插值点必须要共面。 文献[4]将多边形区域分割成若干个三角形来研究多边形上的分形插值问题，而且插值节点是任意的。 文献[5]用三角剖分的方法够构造分形插值曲面，同时提出了两种迭代算法。文献[6]首先提出了矩形区域格点上分形插值问题。文献[7]研究矩形区域上边界插值节点共线条件下的分形插值曲面。文献[8]提出二元递归插值曲面的构造方法。文献[9]运用文献[8]中的原理，构造了一些封闭的分形插值曲面。文献[10]把分形插值函数的概念拓展到n+1维。文献[11]在迭代函数系中引用反射变换,给出任意插值节点的分形插值函数的构造方法, 但在此方法中要求纵向尺度因子都相等。 文献[12]给出矩形区域分形插值曲面连续的一般条件, 但由于该条件需要考虑生成的分形插值曲面的边界曲线, 因此它在曲面生成之前无法判断。 对于矩形区域上任意插值节点的情形,文献[13]在迭代函数系中引入函数纵向尺度因子, 从而保证分形插值曲面的连续性。 这种方法摆脱了边界插值点共线和纵向压缩因子相等的局限性，但由于函数纵向尺度因子的引入，使得这类分形插值曲面的维数难以控制。 综观以上研究，在构造插值曲面时，不是在局部区域边界共线的条件下研究, 就是要求纵向尺度因子相等或者尺度因子是一个函数，使得研究有一定的局限性。

基于以往的研究，本文主要讨论矩形区域网格点上任意插值节点、一般常数纵向尺度因子的递归分形插值曲面的构造方法。 首先由插值函数构造递归迭代函数系；紧接着证明该方法构造的迭代函数系有唯一的不变集且此不变集是一个过给定插值点的连续函数图像，即P(xi,yj)=zi,j。最后，给出一个例子来阐述多项式递归分形插值曲面的构造方法，并且通过改变纵向压缩因子的大小可以形象的观察出曲面的粗糙程度的变化。

1 递归分形插值曲面的构造

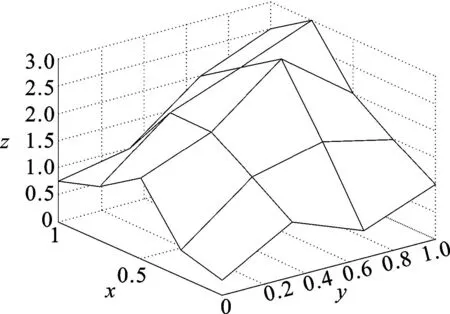
给定闭区间I=[a,b],J=[c,d],E=I×J,设a=x0

Fi,j(x,y,z)=si,jz+ξi,j(x,y),

(1)

其中ξi,j(x,y)是二元多项式，则得到射影

ωi,j(x,y,z)=(φi(x),φj(y),Fi,j(x,y,z)),

i=1,2,…,m;j=1,2,…,n。

(2)

(3)

(4)

且满足如下条件：

P(xi,yj)=zi,j,

i=0,1,…,m;j=0,1,…,n。

(5)

取

(6)

h=0,1,…,p+1;t=0,1,2,…,q+1。则

(7)

设4个一元多项式κ1、κ2、λ1、λ2构成1个二元多项式

由Φ(κ1,κ2,λ1,λ2)(x,y)的构造，易得如下引理1。

2一些重要的引理和定理

引理1设κ1(x)、κ2(x)、λ1(y)、λ2(y)为一元多项式，当κ2(xlx(i))=λ1(yry(j)),κ2(xrx(i))=λ2(yry(j)),κ1(xlx(i))=λ1(yly(j)),κ1(xrx(i))=λ2(yly(j))时，由(8)式计算有:

Φ(κ1,κ2,λ1,λ2)(x,yly(j))=κ1(x);

Φ(κ1,κ2,λ1,λ2)(x,yry(j))=κ2(x);

Φ(κ1,κ2,λ1,λ2)(xlx(i),y)=λ1(x);

Φ(κ1,κ2,λ1,λ2)(xrx(i),y)=λ2(x)。

在函数Fi,j(x,y,z)=si,jz+ξi,j(x,y)中分别取y=yly(j),y=yry(j),x=xlx(i),x=xrx(i),且[xrx(i)-xlx(i)]内有p个插值点,[yry(j)-yly(j)]内有q个插值点,p≥1,q≥1,xlx(i)对应于整个区间于xk,yly(j)对应于整个区间于ys，可以得到4组二元函数。从而可以构造下列4个迭代函数系:

(9)

ξi,s+q(x,yry(j)));

(10)

sk,jz+ξk,j(xlx(i),y));

(11)

ξk+p,j(xrx(i),y))。

(12)

引理2如果迭代函数系(9)—(10)中的多项式

ξi,j(x,y)=P(φi(x),φj(y))-si,jΦ(P(·,yly(j)),P(·，yry(j)),P(xlx(i),·),

P(xrx(i),·))(x,y),

(13)

并且,|si,j|<1，则以上4个迭代函数系都有唯一的不变集。它们分别是函数:

的图像。

证明由(8)、(13)式和引理1，i=k,k+1,…,k+p;j=s,s+1,…,s+q;有

ξi,s(x,yly(j))=P(φi(x),φj(yly(j)))-

si,sΦ(P(·,yly(j)),P(·,yry(j)),

P(xlx(i),·),P(xrx(i),·))(x,yly(j))=

P(φi(x),yj-1)-si,sP(x,yly(j))。

(14)

因此，

Fi,s(x,yly(j),P(x,yly(j)))=si,sP(x,yly(j))+

ξi,s(x,yly(j))=P(φi(x),yj-1)。

定理1设|s|=max{|si,j|∶i=1,2,…,m;j=1,2,…,n}<1,令

ξi,j(x,y)=P(φi(x),φj(y))-si,jΦ(P(·,yly(j)),

P(·,yry(j)),P(xlx(i),·),P(xrx(i),·))(x,y),

其中P和Φ分别由(7)式和(8)式给出，则由以上方法构造的近代函数系(3)有唯一的不变集，并且此不变集是一个过给定插值节点{(xi,yj,zi,j)∶i=0,1,…,m;j=0,1,…,n}的二元函数的图像。

ξi,j(x,yly(j))=P(φi(x),yj-1)-si,jP(x，yly(j));

ξi,j(x,yry(j))=P(φi(x),yj)-si,jP(x,yry(j));

ξi,j(xlx(i),y)=P(xi-1,φj(y))-si,jP(xlx(i),y);

ξi,j(xrx(i),y)=P(xi,φj(y))-si,jP(xrx(i),y),

则

ξi,j+1(x,yly(j))=P(φi(x),yj)-si,j+1P(x,yly(j));

ξi+1,j(xlx(i),y)=P(xi,φj(y))-si+1,jP(xlx(i),y)。

所以,

ξi,j+1(x,yly(j))-ξi,j(x,yry(j))=

P(φi(x),yj)-si,j+1P(x,yly(j))-

P(φi(x),yj)+si,jP(x,yry(j))=

-si,j+1P(x,yly(j))+si,jP(x,yry(j))。

同理，

ξi+1,j(xlx(i),y)-ξi,j(xrx(i),y)=

P(xi,φj(y))-si+1,jP(xlx(i),y)-

P(xi,φj(y))+si,jP(xrx(i),y)=

-si+1,jP(xlx(i),y)+si,jP(xrx(i),y)。

下证

si,jzlx(i),ly(j)+ξi,j(xlx(i),yly(j))=P(xi-1,yj-1)=

zi-1,j-1,si,jzrx(i),ly(j)+ξi,j(xrx(i),yly(j))=

P(xi,yj-1)=zi,j-1,

si,jzlx(i),ry(j)+ξi,j(xlx(i),yry(j))=P(xi-1,yj)=

zi-1,j,si,jzrx(i),ry(j)+ξi,j(xrx(i),yry(j))=

P(xi,yj)=zi,j。

首先证第一个式子。由引理2得si,jzlx(i),ly(j)+ξi,j(xlx(i),yly(j))=P(φi(xlx(i),yly(j)))=P(xi-1,yj-1)，再由(5)式得P(xi-1,yj-1)=zi-1,j-1。其余同理可证。根据文献[12]中定理2.2,令|s|<1对所有的φi,j满足条件|φij(x1,y1)-φij(x2,y2)|≤Lij|x1-x2|αij+Pij·|y1-y2|βij,(x1,y1)、(x2,y2)∈D和sijz00+φij(0,0)=z(i-1)(j-1),sijzm0+φij(1,0)=zi(j-1),sijz0n+φij(0,1)=z(i-1)j,sijzmn+φij(1,1)=zij。则此迭代函数的不变集是连续函数的图象当且仅当(1)φi,j+1(x,0)-φi,j(x,1)=si,jf0(x)-si,j+1fu(x);(2)φi+1,j(0,y)-φi,j(1,y)=si,jfr(y)-si+1,jfl(y)以及推论2.1,在D上的二元连续函数f(文献[12]中定理2.2中的连续函数f)是一个过插值点{(xi,yj,zi,j)}的插值函数，即f(xi,yj)=zij，可知定理成立。

3例子

设E=[0,1]×[0,1]，且E的格点上有如下插值点:

则求得的多项式为：

插值点及分形插值曲面见图1、2。

图1　插值点

图2　分形插值曲面

4 结论

本文运用多项式构造递归分形插值曲面，讨论矩形区域网格点上任意插值节点、一般常数纵向尺度因子的递归分形插值曲面的构造方法。 构造含有常数尺度因子的迭代函数系, 证明该迭代函数系的不变集就是过插值节点的分形插值曲面。 通过实例论证了多项式插值理论的正确性。

参考文献:

[1] BARNSLEY M F. Fractal functions and interpolation[J]. Constructive Approximation,1986,2:303-329.

[2] BARNSLEY M F. Fractal everywhere[M]. New York: Academic Press, 1988.

[3] MASSOPUST P R. Fractal surfaces[J]. Journal of Mathematical Analysis and Applications, 1990, 151:275-290.

[4] GERONIMO J S, HARDIN D. Fractal interpolation surfaces and a related 2D multiresolution analysis[J]. Journal of Mathematical Analysis and Applications,1993,176: 561-586.

[5] ZHAO N L. Construction and application of fractal interpolation surfaces[J]. The Visual Computer, 1996,12:189-212.

[6] XIE H P, SUN H Q, JU Y, et al. Study on generation of rock fracture surfaces by using fractal interpolation[J]. International Journal of Solids and Structures, 2001,38:5765-5787.

[7] DALLA L. Bivariate fractal interpolation functions on grids[J]. Fractals 2001,10 (1): 53-58.

[8] BOUBOULIS P, DALLA L, DRAKOPOULOS V. Construction of recurrent bivariate fractal interpolation surfaces and computation of their box-counting dimension[J]. Journal of Approximation Theory, 2006,141: 99-117.

[9] BOUBOULIS P, DALLA L. Fractal interpolation surfaces derived from fractal interpolation functions[J]. Journal of Mathematical Analysis and Applications, 2007,336: 919-936.

[10] BOUBOULIS P, DALLA L. A general construction of fractal interpolation functions on grids of Rn[J]. European Journal of Applied Mathematics,2007,18: 449-476.

[11] MALYSZ R. The Minkowski dimension of the bivariate fractal interpolation surfaces[J]. Chaos, Solitons & Fractals, 2006,27: 1147-1158.

[12] FENG Z G. Variation and Minkowski dimension of fractal interpolation surface[J]. Journal of Mathematical Analysis and Applications, 2008,345:322-334.

[13] FENG Z G, FENG Y Z, YUAN Z Y. Fractal interpolation surfaces with function vertical scaling factors[J]. Applied Mathematics Letters, 2012,25: 1896-1900.

〔责任编辑宋轶文〕

第一作者： 李雄，男，硕士研究生，研究方向为控制理论、统计模型。E-mail:ica_lixiong@163.com

Construction of recurrent fractal interpolation surfaces with polynomial

KANG yun1， FENG Zhigang1*, GUO Yanfang2

(1 Faculty of Science, Jiangsu University, Zhenjiang 212013, Jiangsu, China;

2 Shanxi College of Applied Science and Technology, Taiyuan 030062, Shanxi, China)

Abstract:A construction of recurrent fractal interpolation surfaces with polynomial is considered. According to the fractal interpolation method, for the given interpolation points, by constructing a proper iterated function system (IFS), a continuous interpolation function, whose graph is an invariant set of the IFS can be obtained. In accordance with the polynomial, iterated function system with constant scaling factors is posed. Then it can be proved that the invariant set of the (IFS) is the interpolation surfaces which passes through interpolation points. By changing the fractal vertical scaling factors, the size roughness of fractal interpolation surface can be regulated.

Keywords:recurrent iterated functions system(RIFS); fractal interpolation surfaces(FIS); bivariate continuous polynomial; invariant set

通信作者：* 李生刚，男，教授，博士生导师。E-mail: topologyli@126.com

基金项目：国家国际科技合作专项基金(2012DFA11270); 海南省国际科技合作专项基金(KJHZ2014-25); 陕西师范大学研究生教育教学改革研究项目(GERP-14-04)

收稿日期：2015-02-14

doi:10.15983/j.cnki.jsnu.2016.01.114

文章编号：1672-4291(2016)01-0019-05

中图分类号：O174

文献标志码：A