模糊集的逻辑等价相似度
2016-02-01段景瑶李永明
段景瑶, 李永明
(1 陕西师范大学 数学与信息科学学院, 陕西 西安 710119;
2 宝鸡文理学院 数学系, 陕西 宝鸡 721013)
模糊集的逻辑等价相似度
段景瑶1,2, 李永明1
(1 陕西师范大学 数学与信息科学学院, 陕西 西安 710119;
2 宝鸡文理学院 数学系, 陕西 宝鸡 721013)
摘要:证明论域X上的全体模糊集之集上的两种度量是等价的。讨论这种度量空间中孤立点的分布情况, 并将这些结论推广到格值模糊集之集上。从模糊推理系统鲁棒性分析的角度, 比较几种不同的蕴涵算子生成的度量或者拓扑。
关键词:正则蕴涵算子; 相似度; 逻辑度量空间; 格值相似度; 鲁棒性
MR subject classification: 03B05;03B52
模糊推理是模糊控制的重要工具。1973年Zadeh提出了模糊推理的CRI方法[1],此后许多学者陆续提出了若干不同的模糊推理方法。1999年王国俊教授提出模糊推理的全蕴涵三I算法[2]。在模糊推理的过程中, 模糊集的选取具有主观性, 所以就产生了模糊推理的鲁棒性问题: 输入的小偏差会引起输出怎样的变化。若小的输入偏差不会导致大的输出偏差, 则称这个系统具有良好的鲁棒性。但是,什么是“小的偏差”?用什么标准去衡量?不同的学者有不同的观点。文献[3]提出模糊集的最大扰动和平均扰动的定义,文献[4]提出连接词的δ-灵敏度,给出模糊推理扰动的最大估计。 由于模糊推理系统的性质主要取决于它的内蕴结构:模糊连接词和蕴涵算子,文献[5-6]提出基于逻辑等价的相似度
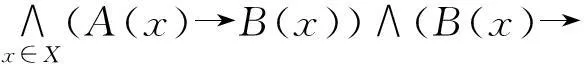
A(x)),A、B∈F(X),
F(X)是论域X上的所有模糊集的全体,→表示[0,1]上的模糊蕴涵。以逻辑等价的相似度作为讨论鲁棒性的指标时用到了逻辑连接词→,这对研究模糊推理系统的鲁棒性赋予了逻辑意义。文献[7-8]在此基础上提出基于逻辑等价的平均相似度
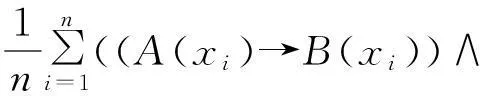
(B(xi)→A(xi))),
A、B∈F(X),X={x1,x2,…,xn},
并证明由4种蕴涵算子诱导的d*(A,B)=1-S*(A,B)可作为F(X)上的度量。在这4种度量空间中讨论了孤立点的分布情况,将4种扰动参数dG*、dR0*、dπ*、dL*作了比较。如果度量空间(F(X),d*)中的孤立点很多, 在孤立点的周围很难找小的扰动,那么如借助参数d*去衡量扰动,就很难讨论推理系统的鲁棒性。那么,对于逻辑等价的相似度S(A,B)而言,1-S(A,B)是否也可作为F(X)上的度量?如果可以,它与1-S*(A,B)有什么关系?此外,以上讨论均是在F(X)上讨论的,能否将这些结论推广到格值模糊集的全体FL(X)上,以便讨论格值推理的鲁棒性?
1F(x)上的两种度量
定义1[9]设L是完备格。二元算子⊗:L2→L被称为是L上的一个T模,如果⊗满足交换律、结合律,对每个变量都不减,且1⊗x=x,∀x∈L。设存在另一个二元算子→:L2→L使得
a⊗b≤c当且仅当a≤b→c,a、b、c∈L,
则称(⊗,→)为L上的伴随对。若L上有伴随对(⊗,→),则称(L,⊗,→)为剩余格。
例1罗列几种[0,1]区间上的重要算子:
(1)a⊗Lb=(a+b-1)∨0,
a→Lb=(1-a+b)∧1;
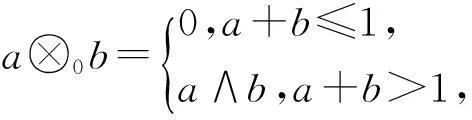
由定义1不难得出,(⊗,→)均为[0,1]上的伴随对,其中⊗∈{⊗L,⊗G,⊗π,⊗0};→对应地取→L,→G,→π,→0。
定义2[7,9-10]设
a↔b=(a→b)∧(b→a),a、b∈L。
a↔b也记作s(a,b)。更一般地,如果L不是剩余格,只是格,→是L上的模糊蕴涵(即→关于第一变量不增,第二变量递减,且0→0=1,0→1=1,1→1=1,1→0=0),也可定义s(a,b)。在文献[3]中,s(a,b)又被记作ρ(a,b),但是ρ(a,a)=1,所以ρ不能作为L上的度量。在L=[0,1]上定义二元算子d:L2→L如下:
d(a,b)=1-s(a,b)=1-(a→b)∧(b→a),∀a、b∈L。
下面的命题1表明例1所述的4种蕴涵诱导的d均可以作为L上的度量。
命题1[7]d0(a,b)=1-s0(a,b)=1-a↔0b=1-(a→0b)∧(b→0a)是[0,1]上的度量。类似地,dL、dπ、dG均为[0,1]上的度量。
命题1中提到常用的4种蕴涵算子可以诱导出[0,1]上的度量,那么其他的蕴涵算子是否也有这种性质?为了讨论这一问题,借助以下的定义2。
定义3[11]设→是[0,1]上的二元运算,如果→满足:
(1)a→b=1当且仅当a≤b;
(2)a≤b→c当且仅当b≤a→c;
(3)a→(b→c)=b→(a→c);
(4) 1→a=a;
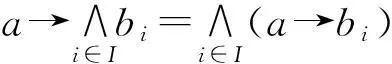
(6)a→b关于b单调递增,关于a单调递减,则称→为[0,1]上的正则蕴涵算子。
定义4[5-6,12]设X是一个非空集合,R是[0,1]上的模糊蕴涵,
∀A、B∈F(X),
称为A、B的R相似度(在不至引起混淆时,可省略下标R,简称为相似度),其中→R是与R相关的蕴涵算子。若SR(A,B)≥δ,则B称为A的一个1-δ扰动。因为SR(A,B)是通过逻辑蕴涵算子构造的,所以把它称为逻辑相似度。若不致产生混淆时,下标R可以去掉。
命题2 设→是[0,1]上的正则蕴涵,如果满足∀a、b∈[0,1],a+a→b≤1+b,则
d(a,b)=1-s(a,b)=1-(a→b)∧(b→a)
是[0,1]上的度量。
证明由于→是正则蕴涵,所以在[0,1]上定义的二元运算⊗:c⊗d=∧{w|c≤d→w},w、c、d∈[0,1],⊗是与→成为伴随对的三角模。∀x、y、z∈[0,1],
参考文献(x↔y)⊗(y↔z)≤x↔z ([9]中定理7.2.14)⟹
(x↔y)≤(y↔z)→(x↔z)(伴随对的性质)⟹
(y↔z)+(x↔y)≤(y↔z)+(y↔z)→(x↔z)(两边同时加上y↔z)≤
1+(x↔z)(由题设条件),
即s(y,z)+s(x,y)≤1+s(x,z),故
d(y,z)+d(x,y)≥d(x,z)。
文献[7-8]中定义的S*(A,B)是对所有s(A(xi),B(xi))(xi∈X,X={x1,x2,…,xn})取平均之后的结果,且以[0,1]上s算子的性质为桥梁,证明4种蕴涵算子按d*(A,B)=1-S*(A,B)的方式导出了F(X)上的度量。
命题3[7-8]设X={x1,x2,…,xn},A、B∈F(X),蕴涵分别取作Gödel蕴涵→G,R0蕴涵→0,Gougen蕴涵→π,Lukasiweicz蕴涵→L时,
d*(A,B)=1-S*(A,B)=
(B(xi)→A(xi))
均是F(X)上的距离度量。
借助命题2,可以将命题3推广为以下推论。
推论1设X={x1,x2,…,xn},A、B∈F(X),→是[0,1]上的正则蕴涵,且满足∀a、b∈[0,1],a+a→b≤1+b,则d*(A,B)均是F(X)上的度量。
在推论1的条件下,对于逻辑相似度S而言,H(A,B)=1-S(A,B)也可作为F(X)上的度量。
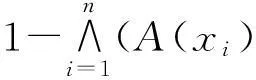
证明(1) 设A、B∈F(X)。显然H(A,B)≥0。若A=B,则∀xi∈X,A(xi)=B(xi)。从而

(B(xi)→A(xi)))=1-1=0。
反之,设H(A,B)=0,则

(B(xi)→A(xi)))=1,
从而∀xi∈X,
(A(xi)→B(xi))∧(B(xi)→A(xi))=1。
因此,∀xi∈X,A(xi)→B(xi)=1,B(xi)→A(xi)=1。故∀xi∈X,A(xi)≤B(xi),B(xi)≤A(xi)。即得∀xi∈X,A(xi)=B(xi),有A=B。
(2) 显然H(A,B)=H(B,A)。
(3)设A、B、C∈F(X),再设
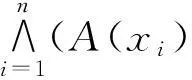
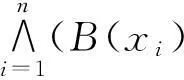
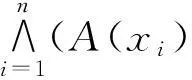
为证明关于H的三角不等式,先证∀A、B、C∈F(X),S(A,B)+S(B,C)≤S(A,C)+1。
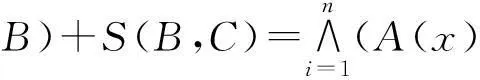
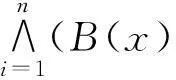
A(xk)↔B(xk)+B(xs)↔C(xs)≤
A(xt)↔B(xt)+B(xt)↔C(xt)≤
A(xt)↔C(xt)+1(由定理1及命题2)=
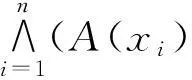
两边同时用2减,即得
H(A,B)+H(B,C)≥H(A,C)。
综上所述,H是F(X)上的一个度量。
注1由命题2及定理1可得,例1中的4种蕴涵算子可按定理1中H的方式诱导出F(X)上的度量。将4种度量依次记作HG、H0、Hπ、HL,不难得出HL≤H0≤HG,HL≤Hπ≤HG,但是H0和Hπ不可比较。
至此,可以借助一些蕴涵算子,在F(X)上用2种方式构造度量,一种是d*, 另一种是H。这2类度量有如下关系。
定理2设X={x1,x2,…,xn},→是[0,1]上的正则蕴涵,且满足∀a、b∈[0,1],a+a→b≤1+b。则F(X)上的2种度量
d*(A,B)=1-S*(A,B)=
(B(xi)→A(xi))和
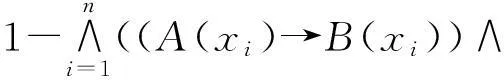
(B(xi)→A(xi)))
等价[14],其中A、B∈F(X)。
证明设B*(A,ε)为度量空间(F(X),d*)中的球形邻域,B(A,ε)为度量空间(F(X),H)中的球形邻域。一方面,∀A∈F(X),ε>0,∀B∈B*(A,ε)令d*(A,B)=ε2。取ε3=ε-ε2,从而∀C∈B(B,ε3)有
d*(A,C)≤d*(A,B)+d*(B,C)≤
ε2+H(B,C)≤ε2+ε3=ε,
第二个不等号成立是因为d*(M,N)≤H(M,N),∀M、N∈F(X)。因此,C∈B*(A,ε),从而B(B,ε3)⊆B*(A,ε)。即对(F(X),d*)的球形邻域,B*(A,ε)中的任意点B都可找到(F(X),H)中的一个球形邻域B(B,ε3)含于其中。故(F(X),d*)中的任意开集均为(F(X),H)中的开集。

H(A,C)≤H(A,B)+H(B,C)≤
ε2+n·d*(B,C)≤
ε2+n·ε3=ε2+ε-ε2=ε。
第二个不等号成立是因为
d*(M,N)=1-S*(M,N)=
(N(xi)→M(xi))=
(N(xi)→M(xi))),
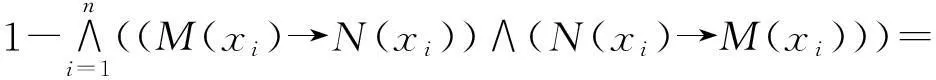
(N(xi)→M(xi))),
得H(M,N)≤n·d*(M,N),∀M、N∈F(X)。
故(F(X),H)中的任意开集均为(F(X),d*)中的开集。
注2由定理2知(F(X),H)与(F(X),d*)的拓扑结构相同,但对于具体的模糊集A与B而言,H(A,B)不一定等于d*(A,B)。例如,A(x1)=0.1,A(x2)=0.2,B(x1)=0.9,B(x2)=0.1,蕴涵算子取作Lukasiewicz蕴涵,得H(A,B)=0.2,d*(A,B)=0.55。H(A,B)使用取小去聚合(A(x1)→B(x1))∧(B(x1)→A(x1)与(A(x2)→B(x2))∧(B(x2)→A(x2),而d*(A,B)使用取平均值的方法去聚合。二者的侧重点不同。
用度量dG*、dR0*、dπ*、dL*作为模糊推理的扰动参数去讨论鲁棒性时,自然要求输入模糊集的微小扰动是存在的,即希望在度量空间(F(X),d*)中输入的模糊集是凝聚点。若(F(X),d*)中的孤立点太多,则参数d*不利于讨论推理系统的鲁棒性。文献[7]分析4种度量空间中孤立点的分布情况,并做了比较。借助定理2,易得以下命题。
命题4设X={x1,x2,…,xn},A∈F(X)。若→是[0,1]上的Gödel蕴涵,则A是(F(X),HG)的凝聚点当且仅当A是X上的正规模糊集;若→是[0,1]上的R0蕴涵,则A是(F(X),HR0)的凝聚点当且仅当A或A′是X上的正规模糊集,这里A′=1-A;若→是[0,1]上的Gougen蕴涵,则A是(F(X),Hπ)的凝聚点当且仅当A≡0;若→是[0,1]上的Lukasiewicz蕴涵,则(F(X),HL)中没有孤立点。
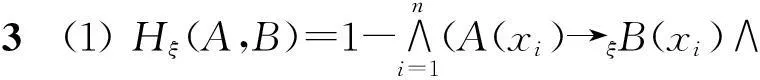
(2) 满足定理1中条件(∀a、b∈[0,1],a+a→b≤1+b)的正则蕴涵,不局限于Gödel、R0、Gougen、Lukasiewicz蕴涵算子。
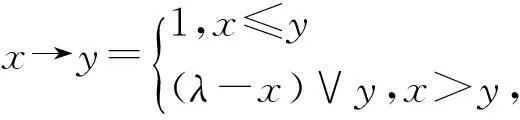

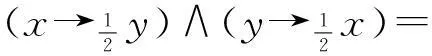

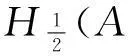

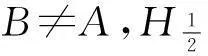

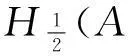

即在A的任意ε-邻域中都有异于A的点,因此A是凝聚点。

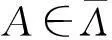

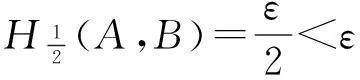


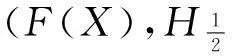
2格值推理的扰动参数
文献[15-16]以剩余格为赋值域,讨论格值推理的若干问题。下面把命题2中的[0,1]区间推广到格上,构造格值推理中的相关扰动参数。
定理3设L是有界格,0是其最小元,1是其最大元。设L-{0}是下定向的。→是其上的模糊蕴涵算子,′是X上的逆序对合对应。∀a、ε∈L,设
B(a,ε)={x∈X|a↔x>ε′},
τ={A⊆L|∀a∈A,∃ε>0,使B(a,ε)⊆A},
则τ是L上的拓扑。
证明(1) 显然,∅∈τ。∀a∈L,B(a,1)⊆L,故L∈τ。
(2) 设A1、A2∈τ,∀a∈A1∩A2,∃ε1∈X且ε1>0,使得B(a,ε1)⊆A1。∃ε2∈X且ε2>0,使得B(a,ε2)⊆A2。因为L-{0}是下定向的,所以∃ε>0使得ε≤ε1,ε≤ε2,由′是逆序的可得ε′≥ε1′,ε≥ε2′。进而B(a,ε)={x∈L|a↔x>ε′}⊆B(a,ε1)∩B(a,ε2)={x∈L|a↔x>ε1′且a↔x>ε2′}。综上,若A1、A2∈τ,则∀a∈A1∩A2,∃B(a,ε)⊆B(a,ε1)∩B(a,ε2)⊆A1∩A2。从而A1∩A2∈τ。

综上所述,τ是L上的拓扑。
如果L是有界全序集,则可保证L-{0}是下定向的。例1中的4种剩余格均满足[0,1]-{0}是下定向的条件。命题2中的度量空间所诱导的拓扑空间恰为定理3中所述的拓扑空间。可把命题2看作定理3的特例。但是,定理3中拓扑空间的建立不仅局限于建立在[0,1]上。如果L是有界格,且L有且仅有一个原子,则L-{0}也是下定向的。

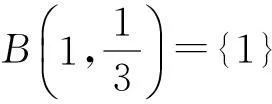
易见,所有单点集都是开集,最终可得τ=φ(L)。即(L,τ)为离散空间。
例3设L={0,θ1,a,b,θ2,1},格序结构与补运算′和例3相同。蕴涵算子为Kleen蕴涵,即x→y=x′∨y,∀x、y∈L。按照定理3中的定义不难得出:
B(0,θ1)={0},B(0,a)=B(0,b)=B(0,θ2)=
{0,θ1),B(0,1)={0,θ1,a,b,θ2};
B(θ1,θ1)=∅,B(θ1,a)=B(θ1,b)=
B(θ1,θ2)={0,θ1},B(θ1,1)=L;
B(a,θ1)=∅,B(a,a)=B(a,b)=B(a,θ2)=
{a},B(a,1)=L;
B(b,θ1)=∅,B(b,a)=B(b,b)=B(b,θ2)=
{b},B(b,1)=L;
B(θ2,θ1)=∅,B(θ2,a)=B(θ2,b)={θ2,1},
B(θ2,θ2)={a,b,θ2,1},B(θ2,1)=L;
B(1,θ1)={1},B(1,a)=B(1,b)=B(1,b)=
{θ2,1},B(1,θ2)={a,b,θ2,1};
B(1,1)={a,b,θ1,θ2,1}。
可以按照定理6中τ的结构做出拓扑,但这个拓扑空间不是离散空间,因为{θ1}、{θ2}∉τ。
下面把定义4中的模糊集换成格值模糊集,在FL(X)上建立两个模糊集之间的似度以及距离的概念。
定义5设X是一个非空集合,L是一个完备格。→是L上的蕴涵算子,∀A、B∈FL(X),令

(B(x)→A(x))。

定理4设X是一个非空集合,L是有界全序格,0是其最小元,1是其最大元,L-{0}是下定向的。→是其上的模糊蕴涵算子,′是L上的逆序对合对应。设A∈FL(X),ε∈L,ε>0。若令B(A,ε)={B∈FL(X)|S(A,B)>ε′},τ={R⊆FL(X)|∀A∈R,∃ε∈L且ε>0,使得B(A,ε)⊆R},则τ是FL(X)上的拓扑。
证明(1) 显然{∅}∈τ,∀A∈FL(X),B(A,1)⊆FL(X),故FL(X)∈τ。
(2) 任取R1、R2∈τ,∀A∈R1∩R2,因为A∈R1故∃ε1>0使得B(A,ε1)⊆R1。因为A∈R2故∃ε2>0,使得B(A,ε2)⊆R2。因为L-{0}是下定向的,故∃ε>0,使得ε≤ε1,ε≤ε2,由′是逆序的,所以ε1′≤ε′,ε2′≤ε′,从而
B(A,ε)={C∈FL(X)|d(A,C)<ε}=



B(A,ε1)∩B(A,ε2)⊆R1∩R2
由τ的定义知,R1∩R2⊆τ。
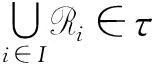
至此,在格值模糊集之集FL(X)上构造了拓扑,下面,针对不同的蕴涵算子,讨论不同拓扑空间的结构,并作以分析。
定理5设X={x1,x2,…,xn},(L,→,′,∨)是全序的R0代数,0是其最小元,1是其最大元。A∈FL(X)。若A是拓扑空间(FL(X),τ)的凝聚点,那么A或A′是正规模糊集。这里A′(x)=(A(x))′。


定理6设X={x1,x2,…,xn}。(L,→,′,∨)是全序的Gödel代数。0是其最小元,1是其最大元。若A是拓扑空间(FL(X),τ)的凝聚点,那么A是正规模糊集。
假设A不是正规模糊集,则∀xi∈X,0≤A(xi)<1。又若B≠A,则∃xk∈X,使B(xk)≠A(xk)=αk,0≤αk<1。从而(A(xk)→B(xk))∧(B(xk)→A(xk))≤A(xk)=αk。故S(A,B)≤αk<1,H(A,B)≥αk′>0。对任意的B≠A,取δ=α1′∧…∧αn′,有H(A,B)≥δ>0。又因为B(A,δ)={C∈FL(X)|H(A,C)<δ}={A},故B(A,δ)∈τ,从而B(A,δ)是A的开邻域,但是B(A,δ)∩(X-{A})=∅,故A不是凝聚点。


因此,在上述两个拓扑空间(FL(X),τ)中A均不是凝聚点。
由上述定理及例子可知,在上述两个拓扑空间(FL(X),τ)中,若A或A′是正规模糊集,则A才有可能是凝聚点。FL(X)中的模糊集有很多,正规模糊集或者正规模糊集的补集只是很少一部分。并且,由上述例子看到, 即便A是正规模糊集也不能保证A在这两个拓扑空间中是凝聚点。
4结论

[1] ZADEH L A. Outline of a new approach to the analysis of complex systems and decision processes[J]. IEEE Transactions Systems, Man and Cybernetics. 1973, 1: 28-44.
[2] 王国俊.模糊推理的全蕴涵三I算法[J].中国科学(E辑),1999,29(1):43-53.
[3] CAI K Y. Robustness of fuzzy reasoning and δ-equalities of fuzzy sets[J].IEEE Transactions on Fuzzy Systems, 2001, 9(5): 750-783.
[4] LI Y M, LI D C, WITOLD P, et al. An approach of measure the robustness of fuzzy reasoning[J]. International Journal of Intelligent Systems, 2005, 20: 393-413.
[5] 金检华,李永明,李春泉.模糊推理系统的鲁棒性[J]. 模糊系统与数学, 2008, 22(5): 80-91.
[6] JIN J H, LI Y M, LI C Q. Robustness of fuzzy reasoning via logically Equivalence measure[J].Information Sciences, 2007, 177: 5103-5117.
[7] 王国俊,段景瑶.适宜于展开模糊推理的两类模糊度量空间[J].中国科学:信息科学,2014, 44:623-632.
[8] WANG G J, DUAN J Y. On robustness of the full implication triple I inference method with respect to finer measurements[J]. International Journal of Approximate Reasoning, 2014, 55: 787-796.
[9] 王国俊.非经典数理逻辑与近似推理[M].2版.北京:科学出版社,2008.
[10] KLEMENT E P,MESIAR R,PAP E.Triangular norms[M]. Dordrecht: Kluwer Academic Publishers, 2000.
[11] 王国俊.数理逻辑引论与归结原理[M].2版. 北京:科学出版社, 2009.
[12] DAI S S, PEI D W, DUO D H. Robustness analysis of full implication inference method[J]. International Journal of Approximate Reasoning. 2013, 54: 653-666.
[13] 任芳. 正则蕴涵算子与新型模糊逻辑系统的研究[D]. 西安: 陕西师范大学数学与信息科学学院, 2005.
[14] 熊金城. 点集拓扑[M].3版. 北京:科学出版社, 2003.
[15] PAN H Y, LI Y M, CAO Y Z. Lattice-valued simulations for quantitative transition systems[J]. International Journal of Approximate Reasoning, 2015, 56: 28-42.
[16] PAN H Y, CAO Y Z, ZHANG M, et al. Simulation for lattice-valued doubly labeled transition systems[J].International Journal of Approximate Reasoning, 2014, 55: 797-811.
〔责任编辑宋轶文〕
第一作者: 崔东,男,硕士,研究方向为金属材料的超声检测。E-mai:18192507400@189.cn
第一作者: 康云,女,硕士研究生,研究方向为分形几何理论。E-mail:976979936@qq.com
Similarity degree via logic equivalence of fuzzy sets
DUAN Jingyao1,2, LI Yongming1
(1 School of Mathematics and Information Science, Shaanxi Normal University,
Xi′an 710119, Shaanxi, China;
2 Department of Mathematics, Baoji University of Arts and Sciences, Baoji 721013, Shaanxi, China)
Abstract:The equivalence of two metrics on the family of fuzzy subsets of the universe X is verified. The distributions of isolated points of the above metric spaces are discussed, and these investigations were extended to the set that consist of lattice-valued fuzzy subsets. Different metrics or topologies which generated by different implication operators are compared from the view point of robustness analysis of fuzzy reasoning system.
Keywords:regular implication operators; similarity degree; logic metric spaces; lattice-valued similarity degree; robustness
通信作者:* 贺西平,男,教授,博士生导师。E-mail:Hexiping@snnu.edu.cn * 冯志刚,男,教授。E-mail:zgfeng0511@gmail.com
基金项目:国家自然科学基金(11374201) 国家自然科学基金(51079064)
收稿日期:2015-09-10 2015-03-05
doi:10.15983/j.cnki.jsnu.2016.01.211 10.15983/j.cnki.jsnu.2016.01.113
文章编号:1672-4291(2016)01-0024-05 1672-4291(2016)01-0014-05
中图分类号:O159;O189.1
文献标志码:A
