基于因素分解的个人所得税再分配效应分析

◆黄桂兰

基于因素分解的个人所得税再分配效应分析

◆黄桂兰

文章对Kakwani（1977）税收再分配效应进行分解发现，税收是否具有累进性是个人所得税实现收入公平功能的决定因素。税收在具有累进性的前提下，改变平均税率或税收累进性是改变税收再分配效应的两个重要途径。但是现有研究过多的关注累进性及其分解而忽视平均税率及其分解，鲜少研究平均税率对再分配效应的贡献程度，也难分解因素的贡献排名。将Hossian（2011）洛伦茨拟合方程引入基尼系数的测算，运用VAR模型和方差分解，发现税收规模、平均税率和税收累进性对个人所得税再分配效应的贡献程度不同，税收规模和平均税率的变动对再分配效应的影响远大于累进性，提高税收规模或平均税率比提高累进性带来更显著的调节效果。在现阶段累进性较高的前提下，扩大税收规模或者挖掘税收规模潜力，能够为改善个人所得税再分配效应和推进个人所得税改革提供有力的技术支持。

个人所得税；再分配效应；洛伦茨拟合曲线；税收规模

一、引言

2016年10月10日，国务院发布的《关于激发重点群体活力带动城乡居民增收的实施意见》指出“逐步建立综合和分类相结合的个人所得税制度，进一步减轻中等以下收入者税收负担，发挥税收调节功能”，使得个人所得税改革以及发挥个人所得税的实际再分配效应再次成为舆论关注的焦点。从1980年个人所得税法颁布到2011年的第五次修订，我国个人所得税的实际角色为“累进性突出，公平性不足”，即税制累进性较高，再分配功能却基本丧失。国内研究将个人所得税再分配效应不足的原因归结为税收规模不足以达到有效的调节效果，但是缺乏可靠且有力的证据。

Kakwani（1977）将个人所得税收入再分配效应分解为平均税率和累进性。由于税收累进性对税收政策的导向性更为直接，使得税收累进性成为税收再分配效应研究中最核心的概念。Musgrave et al.（1948）在Pigou（1928）的基础上，沿用和扩展了古典累进性方法论。Kakwani（1977）、Suit（1977）以不同的税收集中度曲线为基础提出了以K指数和S指数为代表的现代累进性方法论。伴随着税收累进性方法论的研究，利用累进性指标对税收体系及税种累进性贡献因子的挖掘也紧随其后。Oberhofer（1975）、Kakwani（1984）、Pfahler（1990）、Aronson 和 Lanmber（1994）、Lambert et al.（1997）等分别在前人研究的基础上完善了单一税种累进性的分解，将累进性分解为税制因素——排除项目（非应税所得）、免征额、税率结构、费用扣除。彭海燕（2010）在Loizide（1980）和Pfahler（1990）在单一税种已有累进性分解的基础上，加入了新的“偷逃税”因素，将应纳税额的累进性分解为税率、扣除额、税收抵免、逃税效应四个因素，丰富了税种累进性的分解。岳希明等（2012）在税前收入排序的基础上，对K指数进行了适用性简化分解，将K指数分解为税率结构和费用扣除两个部分。在各分解因素中，税率结构是决定税收累进性的决定因素（Wagstaff et al，2001；Urban，2005）。Verbist（2004）发现个人所得税的平均税率与税制的累进程度K之间存在显著的负相关关系，平均税率高的国家偏好累进程度低的税制结构，反之，平均税率低的国家偏好累进性高的税制结构。

但是再高的税收累进性都会因较小的平均税率损害税收的调节功能，也就是说平均税率的高低是个人所得税再分配效应的决定因素，累进性是次要因素（岳希明，2011；石子印，2014），那么对平均税率及其分解的研究就显得尤其重要。然而，现有研究过多的关注累进性及其分解而忽视平均税率及其分解，鲜少研究平均税率对再分配效应的贡献程度，也难有对再分配效应分解因素的贡献排名。

二、理论分析与模型构建

根据Kakwani（1977）对税收再分配效应的分解，税收再分配效应与平均税率和累进性存在如下关系，

其中，RE为税收再分配效应， Ginib为税前基尼系数， Ginia为税收基尼系数，t为平均税率，K为税收累进性指数。

RE是(t,K)的函数，分别对t和K求偏导：

由(2)、(3)式可知，税收是累进的（K＞0），是税收再分配效应的必要条件。在税收是累进的前提下，改变平均税率或税收累进性是改变税收再分配效应的两个重要途径。如果税收政策的目的在于更好地实现个人所得税的再分配功能，那么可以在既定累进性水平下，提高平均税率；也可以在既定平均税率条件下，提高现有累进性水平（降低低税率，提高高税率），而且提高平均税率有可能比提高累进性带来更大的调节效果；当然也可以既提高平均税率又提高累进性；但是，当累进性指数K＜0时，再高的平均税率也只是进一步扩大收入差距，公平性的税收政策不仅徒劳而且会损害社会公平。因此，K＜0（(3)式）不在本研究的范围之内。

由(2)式可以看出平均税率不仅影响税收再分配效应，同时也影响累进性指数K对税收再分配效应的贡献程度。

平均税率t是个人所得税T和税前收入Y的函数。

由以上分析可以看出，在税收是累进性的前提下，再分配效应与平均税率和税收规模严格正相关，税收规模和平均税率与税收累进性的关系不明确。除此之外，各因素对税收再分配效应的贡献程度也不明确。李林木等（2013）使用Person相关系数仅考察了各因素与税收再分配效应的符号关系，没有明确的数量程度，①这是因为Person相关系数仅考察变量之间是否具有显著的相关关系，而不具有明确数量关系。为了确定各因素对收入再分配效应的贡献，本文引入结构向量自回归模型VAR和方差分解。

P阶4变量的结构向量自回归模型VAR（P）的向量表达式为：

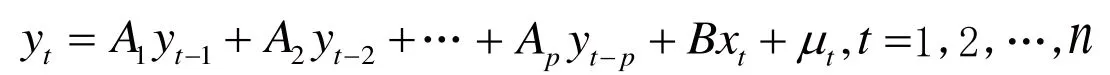
其中，

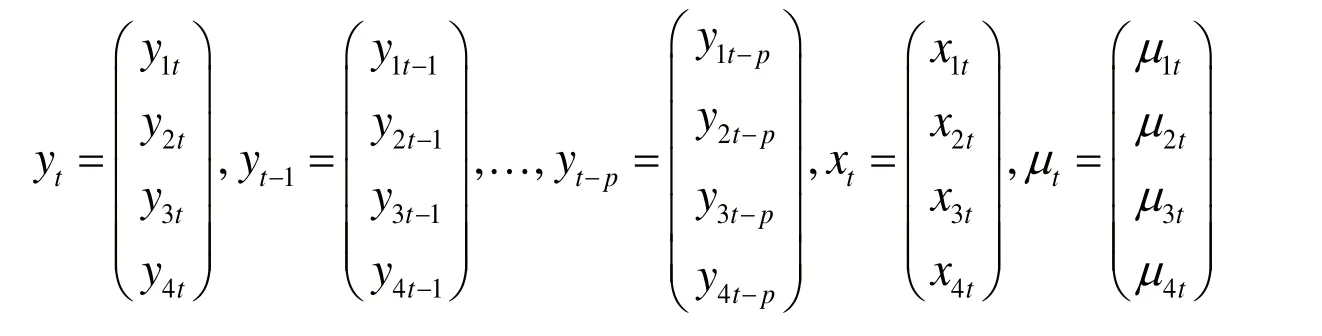
三、变量定义与基础数据选取

（一）变量定义和测算方程

REt、rt、Kt、Tt分别代表税收再分配效应、个人所得税平均税率、个人所得税税收累进性、个人所得税税收规模。全部变量个数为4，μ1t、μ2t、 μ3t、μ4t分别作用于REt、rt、kt、Tt的结构式冲击。

1.洛伦茨曲线拟合方程的选择

由于我国收入分组数据较少，为了提高基尼系数的精确度，选用洛伦茨曲线拟合法对居民收入不平等的离散数据进行拟合。选用Hossain（2011）拟合函数，因为该函数满足洛伦茨曲线的所有特性，针对分组数据的拟合度R2优于其他模型（如Kakwani et al.，1976；Rasche et al.，1980；Ortega et al.，1991）。

Hossain（2011）洛伦茨曲线拟合函数为：

其中，x为人口累计百分比， f( x)为收入累计百分比，α、β、θ为参数，且 a＞0,β ＞0,0 ＜θ≤1。

2.基尼系数测算方程的选择

基尼系数测算方法有上梯形面积法、下梯形面积法、直接法等。在洛伦茨曲线已知的条件下，下梯形面积法是最为实用的方法（王亚芬等，2007；古建芹等，2011），故选择使用下梯形面积法为基尼系数的测算方法。

变量定义及具体测算方程如表1。

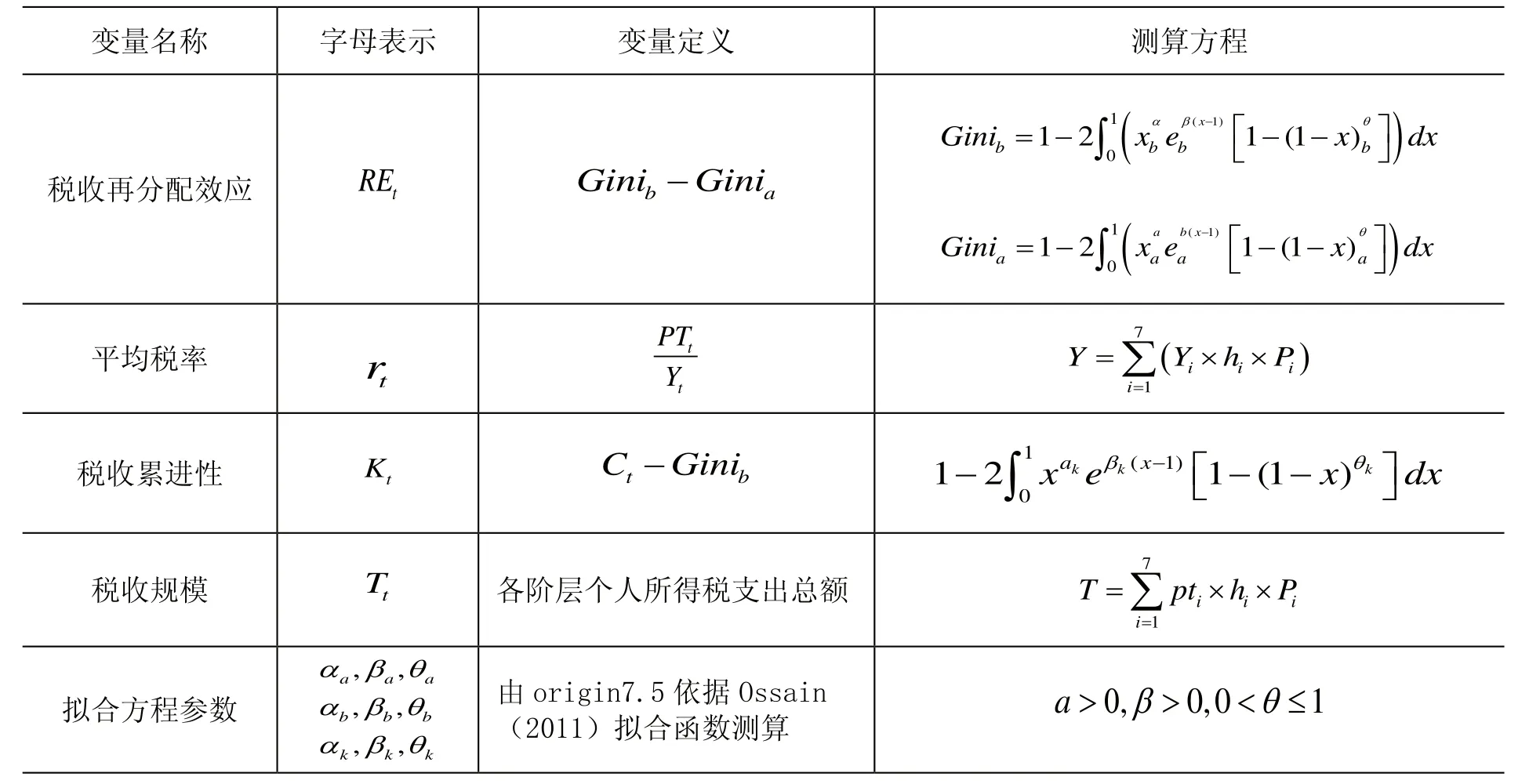
表1 变量定义和测算方程

（二）基础数据的来源和处理

各时间序列（变量）中的 REt、 Kt的基础数据来源于《中国城市（镇）生活与价格年鉴》和《中国住户调查年鉴》； rt、 Tt的基础数据来源于《中国统计年鉴》和《中国税务年鉴》。基于数据的可得性和连续性，选取的时间跨度为1995—2011年。由于各因素与再分配效应存在非线性关系，使用对数化处理；基础数据水平值均在剔除1995年物价指数的基础上进行对数处理，以便在同一基准上进行比较。利用origin7.5测算洛伦茨曲线参数和各变量，使用eviews7.0估计VAR模型的系数和方差分解。

四、实证检验与结果分析

（一）各变量测算值

由各变量测算值可以看出，税收累进性整体呈下降趋势；平均税率与个人所得税再分配效应都呈现相同的向上趋势，税收累进性下降，个人所得税再分配效应由平均税率决定。1995—2005年，税收累进性快速下降，但是平均税率快速上升，带动着个人所得税再分配效应迅速上升，2006—2011年，平均税率的增长速度有所下降，个人所得税再分配效应的增长速度明显下降，然而这一阶段累进性先上升后缓慢下降。两个阶段个人所得税再分配效应的增长速度都不及平均税率，说明累进性的下降在一定程度上抵消了平均税率对个人所得税再分配效应的贡献。在整个区间内平均税率与累进性的变动趋势相反，说明两者存在明显的负相关关系，这与Wagstaff（1999）、Verbist（2004）的研究结论相一致。

表2 个人所得税再分配效应分解

图1 RE与r和K指数的关系

（二）VAR模型的预估计

由于“伪回归”存在，在进行模型回归分析前必须对各变量进行平稳性检验。并且，结构向量自回归模型本身要求具有稳定性。为此按照要求对变量和模型进行检验，并以此为基础进行脉冲响应和方差分解。

1.变量的平稳性检验

使用ADF对变量的平稳性进行检验，检验类型（C，T，L）中的截距项C、趋势项T由各变量时间序列的时序图确定，滞后阶数L根据eviews7.0中的AIC自动确定最优值。

表3 变量及差分序列平稳性的ADF检验结果

注：d代表时间序列的一阶差分形式；**表示5%显著性水平下拒绝一阶差分序列有单位根的假设。

在5%显著性水平上，各变量均接受了有单位根的原假设，表明各变量是不平稳的。经过一阶差分后的时间序列均拒绝有单位根的原假设，表明各变量的一阶差分序列是平稳的，即各变量是一阶单整的，说明各时间序列明显存在均衡关系，可以建立VAR模型。

2.模型估计

对模型进行OLS回归得到再分配效应因素分解的VAR模型，并写成如下向量式：

（三）VAR模型的稳定性检验

建好VAR模型后，需要检验被估计的VAR模型是否恰当，对VAR模型进行滞后结构检验。在确定合理的滞后阶数P后，还需进行AR根检验和Granger格兰杰因果检验。

1.最优滞后阶数的确定

经过滞后排除检验，绝大部分的滞后阶数处在2阶，而且用于模型估计的AIC和SC准则都处在滞后2阶，可以确定因素分解VAR模型的最优滞后阶数为2阶。

表4 最优滞后阶数的确定

2.模型的稳定性检验

由于最优阶数和模型估计时所使用的阶数相同，所以VAR（2）模型OLS估计是有效的。各估计系数可以解释变量之间的相关关系，可以进行模型的稳定性检验。

VAR模型所有根的倒数都落在了单位圆内，所建立的因素分解模型是稳定的，因而可以进行脉冲响应分析和方差分解。

图2 VAR模型稳定性判定

3.Granger因果检验

进行格兰杰因果检验的目的是确定各变量之间是否具有因果关系。只有通过格兰杰因果检验才可以判定出一个变量y在多大程度上被另一个变量x的过去值所解释，即加入变量x的滞后期后是否提高了解释力度。

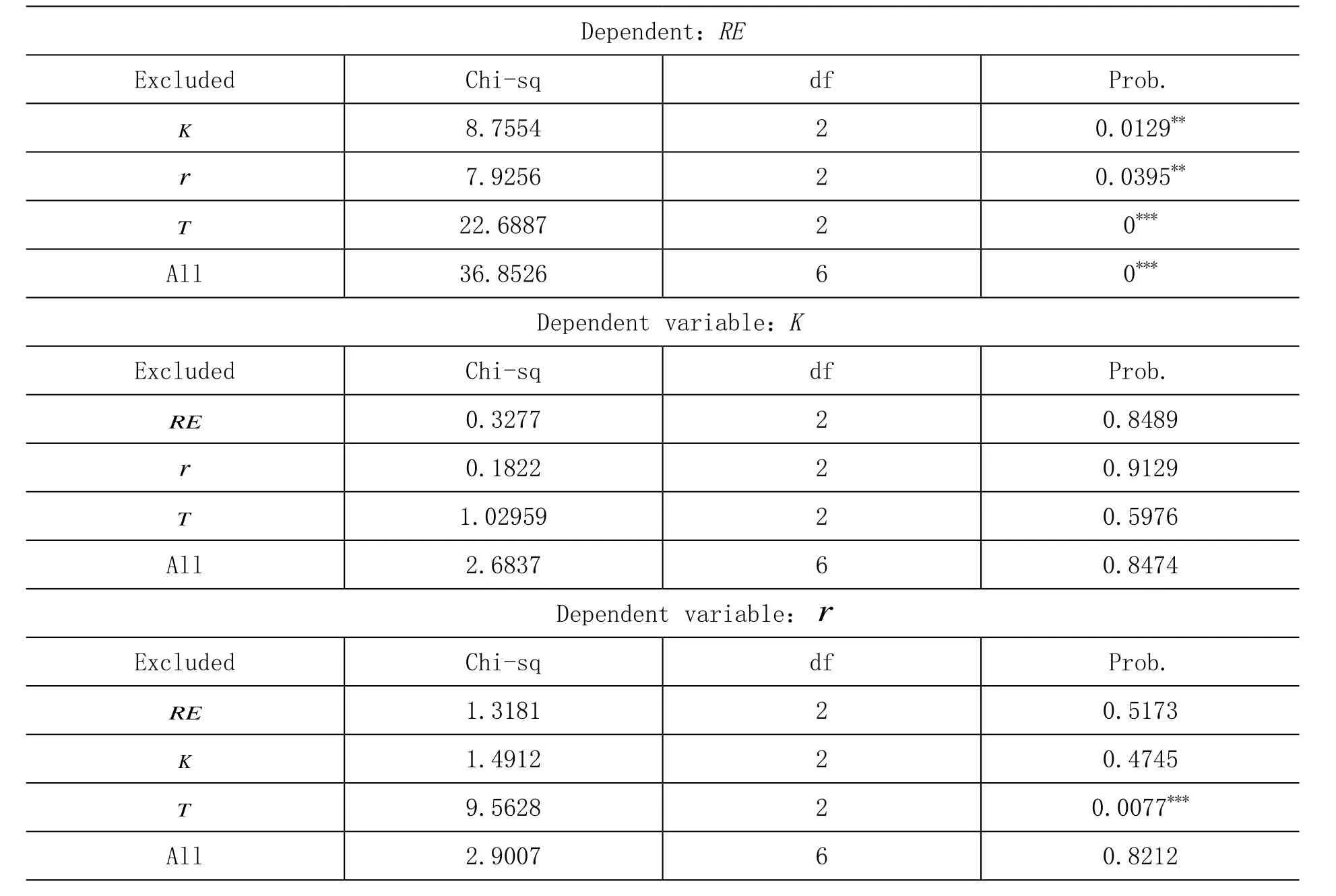
表5 格兰杰因果检验

注：***和**分别表示1%和5%显著性水平下拒绝“不存在因果关系”的假设。

在对格兰杰因果检验结果进行分析前，必须明确一点，稳定的VAR模型与变量之间进行因果检验是有显著区别的，变量之间进行的因果检验是考察变量间的因果关系是否显著。在稳定的VAR模型基础上进行因果检验，首先，对VAR模型中的某个因变量或内生变量是否具有成为自变量或者外生变量的可能性进行检验，是“单个变量”当期和滞后期的联合检验；其次，每个方程右边所有内生变量对目标变量是否可以成为外生变量，是“所有”内生变量当期和滞后期的联合检验。从这个意义上说，RE作为自变量的因果检验拒绝了其他变量不能Granger引起RE的备择假设，也就是说RE作为自变量不仅通过了单个变量同期的联合检验，也通过了所有变量同期的联合检验，这也与上文的理论分析相一致。其他变量的因果检验都接受了不存在因果关系的结论，这同税收再分配效应与平均税率和累进性以及平均税率和税收规模的关系较为一致。

（四）脉冲响应分析

在VAR模型中，脉冲响应函数可以用来描述一个内生变量对误差项所带来的冲击反应，即在随机误差项上施加一个标准大小的冲击后，对内生变量的当期值和未来值产生的影响程度，这是因为冲击会通过滞后结构传递给其他变量，以冲击的方式描绘变量间的动态路径。

因素分解的脉冲响应函数选择滞后长度为5期，为了分析税收累进性、平均税率和税收规模对个人所得税再分配效应的长短期影响的差异，采用Monte Carlo模拟100次来研究冲击的动态响应。①陈灯塔：《应用经济计量学》，北京：北京大学出版社，2012年版，第520页。

对于稳定的VAR模型，信息的脉冲响应趋于0，累计响应趋于非0常数，个人所得税再分配效应对税收累进性的响应是正向的，短期内有所波动，第一期到第四期先下降后上升，冲击的反应较小，在第4期后冲击反应为零，这说明税收累进性对个人所得税的冲击影响是正的短期效应，也就是说增加税收累进性有利于个人所得税再分配效应的提高。从累计响应看，税收的再分配效应并非严格等于零，对累进性的冲击较为不敏感，甚至有可能降低再分配效应，我国个人所得税的累进性均值为0.38，表现出来的个人所得税的公平性较高，但是平均税率较低，使得个人所得税的调节效果并没有达到高累进性应达到的调节效果，当累进性达到一定程度时，反而会使得再分配效应下降（Verbist，2004）。由平均税率和税收规模对个人所得税再分配效应的冲击图可以看出，平均税率和税收规模的冲击具有一致性，两个因素对个人所得税再分配效应长期影响是正向的，在短期内是负向的，而且负向的响应时间较短，只维持了2期，随后开始2期的正向短期效应，这与我国统计区间内的个人所得税占GDP的比重有关。1994—1999年，个人所得税宏观平均税率从0.15%上升至0.46%，随后增长至1%；2002—2012年，出现停滞状态，维持在1%～1.25%之间，较小的平均税率使得个人所得税再分配效应较小，不足以显现其效果。但是，税收规模对税收再分配效应的冲击是明显的，在冲击中税制改革的反应也是微弱的，而且会迅速地回归到原有的趋势。除此之外，个人所得税的扭曲程度（个人所得税增长率超GDP增长率）也影响了个人所得税再分配效应的程度；税收规模的累计响应大于平均税率，这与税收规模与平均税率的正相关完全符合。无论短期还是长期各因素的增加都有利于个人所得税再分配效应的增加。

图3 税收累进性、平均税率和税收规模对RE信息的响应

图3和图4为税收累进性、平均税率和税收规模对个人所得税再分配效应的各期响应和累计响应，其中，横轴表示时间，纵轴表示冲击的响应程度。

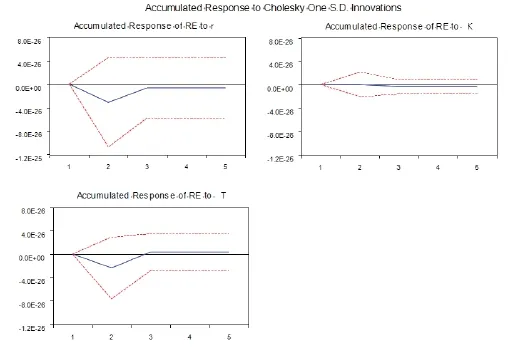
图4 税收累进性、平均税率、税收规模对RE信息的累计响应

（五）因素贡献分解

在脉冲响应函数分析的基础上，可以使用方差分解求得各因素对个人所得税再分配效应的贡献程度。

方差分解模型为：

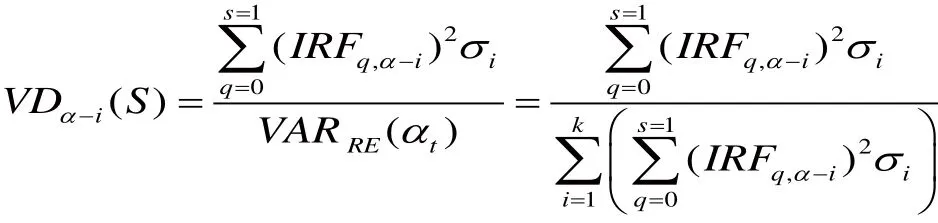
其中，i=1，2，3，4分别表示个人所得税再分配效应RE、个人所得税累进性K、个人所得税平均税率r、个人所得税税收规模T，V Dα-i(S )为个人所得税再分配效应的方差贡献率， VARRE(αt)为个人所得税再分配效应RE的方差，S为滞后区间， IRFq,α-i是个人所得税再分配效应对第i个变量冲击的脉冲响应函数， σi为第i个变量的标准差。方差分解的判定方法为： VDα-i(S )较大时，第i个变量对个人所得税再分配效应的贡献率大，反之，贡献率小。

为了考察各要素对税收再分配效应贡献的长期趋势预测，选择预测期为10期。

表6 个人所得税再分配效应的方差分解

图5 税收累进性、平均税率、税收规模对RE的贡献率

税收规模的冲击引起的个人所得税再分配效应的作用一直大于平均税率和税收累进性，而且对个人所得税的贡献率经历了先升后降再升的趋势，表明税收规模对个人所得税再分配的贡献率在强化，从第10期开始，个人所得税再分配效应的预测方差的20.34%由税收规模的变动来解释，9.06%由平均税率的变动来解释，4.79%由累进性的变动来解释。税收累进性对个人所得税的贡献率经历了先上升后下降的倒U型趋势，说明未来如果想通过提高累进性而增加再分配效应的预测方差，其结果是不理想的，只会降低税收累进性的贡献率。个人所得税再分配效应对自身的方差分解有较大的贡献，反映出个人所得税再分配效用对自身的一个标准差信息也会有较大的正向响应，但是这个贡献率在迅速下降，自身贡献率的下降迅速地被税收规模所代替。因此，在税制累进性已经较高的前提下，扩大税收规模或挖掘税收规模的潜力是提高再分配效应的唯一途径。

（六）VAR模型的优化

对个人所得税再分配效应进行的方差分解足以说明税收累进性、平均税率、税收规模对个人所得税的贡献程度，但是由于我国个人所得税再分配效应较小，平均税率较低，VAR模型的各变量滞后期对方程左边变量的回归系数影响较小，格兰杰因果检验又否定了外生变量（税收累进性、平均税率和税收规模）之间的因果关系，所以本文最后对所构造的VAR模型进行优化，剔除系数较小，因果关系不明的当期变量或滞后变量。

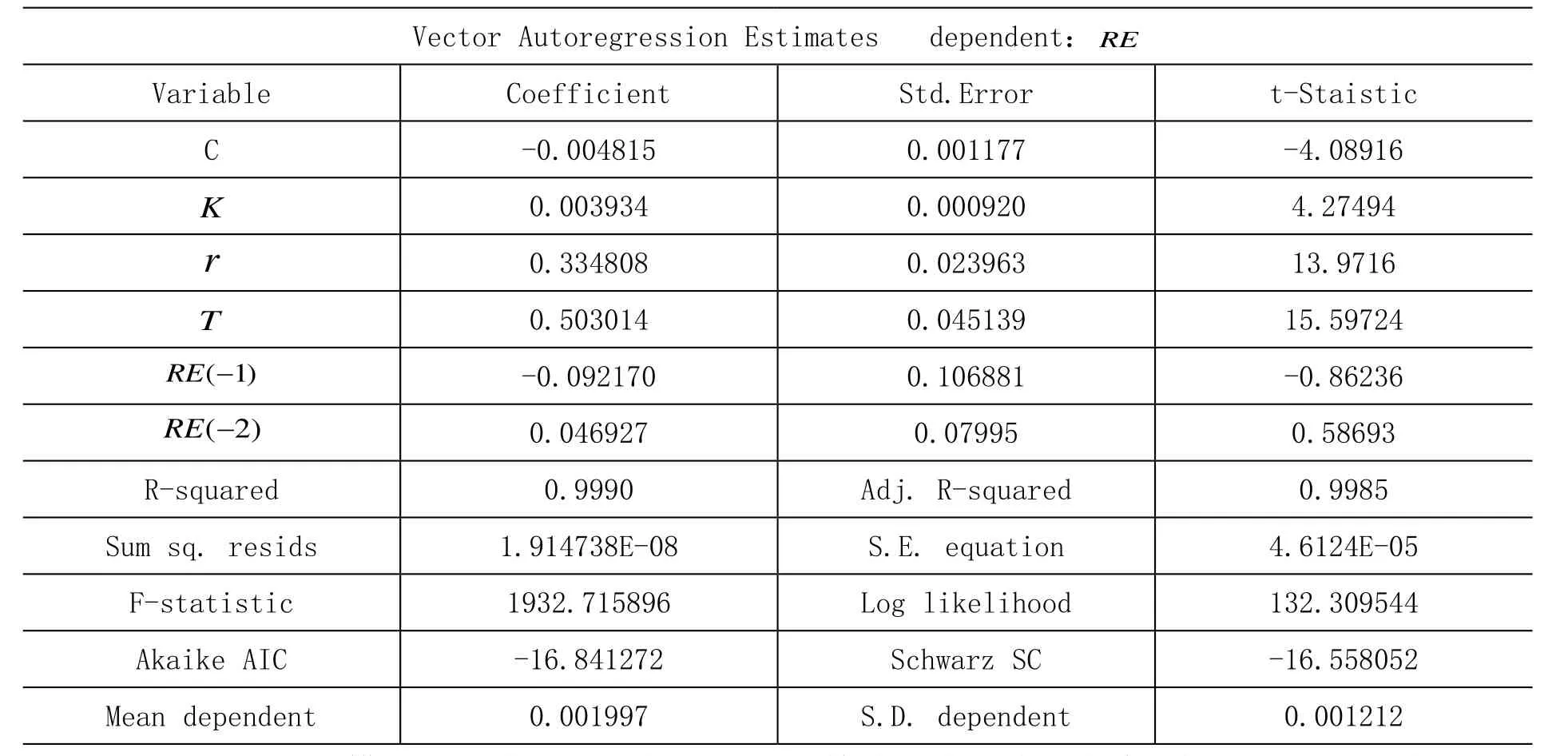
表7 优化的VAR模型估计结果

对于优化的VAR模型，经过滞后期确定和AR根检验，确定其具有稳定性。由预测方差可知要素对税收再分配效应未来的贡献率，而对现有税收再分配效应的分析更加具有实际意义。从优化的VAR估计结果可以看出，在税收是累进的前提下，税收规模对税收再分配效应的贡献最大，税收规模变动1%，个人所得税再分配效应增长0.503%；平均税率变动1%，个人所得税再分配效应增长0.335%；累进性增长1%，个人所得税再分配效应增长0.0039%；同时验证了提高平均税率和税收规模比提高累进性能带来更有效的调节效果。

五、结论

从个人所得税再分配效应分解理论和VAR模型分析可以得出以下结论：

第一，在税收是累进性的前提下，平均税率、税收规模和累进性与个人所得税收入再分配效应存在着严格的正相关关系，税收累进性是个人所得税是否具有收入公平功能的决定因素，而税收规模是个人所得税分配效应大小的决定因素。

第二，1995—2011年，税收累进性整体呈下降趋势；平均税率与个人所得税再分配效应都呈现向上趋势，但个人所得税再分配效应的增长速度不及平均税率，说明累进性的下降在一定程度上损害了再分配效应；在整个区间内平均税率与累进性的变动趋势相反，说明两者存在明显的负相关关系。

第三，由方差分解可知税收规模对个人所得税再分配效应的贡献率在三因素中是最大的，在10期内经历了先升后降再升的趋势，表明税收规模对个人所得税再分配效应的贡献率在强化，再分配效应预测方差的20.34%由税收规模的变动来解释，9.06%由平均税率的变动来解释，4.79%由累进性的变动来解释。而税收累进性对个人所得税的贡献率经历了先上升后下降的“倒U型”趋势，说明未来如果想通过提高累进性而增加再分配效应，其结果是不理想的，只会降低税收累进性的贡献率。

第四，在税收是累进的前提下，税收规模变动1%，个人所得税再分配效应增长0.503%；平均税率变动1%，个人所得税再分配效应增长0.335%；累进性增长1%，个人所得税再分配效应增长0.0039%；这也验证了提高平均税率和税收规模比提高累进性能带来更显著的调节效果。

总之，个人所得税是累进的是实现税收再分配效应的必要条件，税收规模是决定税收再分配效应大小的决定性因素，在其他条件不变下，提高税收规模或平均税率比提高累进性能带来更大的再分配效应。

[1]Oberhofer.The Redistributional Effect of the Federal Income[J].National Tax Journal，1975,28(1)：127-33.

[2]Kakwani，N.On the Measurement of Tax Progressivity and Redistribution Effect of Taxes with Applications to Horizontal and Vertical Equality[J].Advances in Econometrics，1985，42(2)：149-168.

[3]Pfähler，W.Redistributive Effect of Income Taxation：Decomposing Tax Base and Tax Rates Effects[J].Bulletin of Economic Research，1990，42(2)：3307-3378.

[4]Aronson，J.R，Lambert P.J. Decomposing the Gini Coefficient to Reveal the Vertica，Horizontal and Reranking Effects of Income Taxation [J]. National Tax Journal，1994,47(2)：273-294.

[5]岳希明，徐 静，刘 谦，丁 胜，董丽娟.2011年个人所得税改革的收入再分配效应[J].经济研究，2012,(9).

[6]Sharif Hossain，Chikayoshi Saeki.A New Functional Form for Estimating Lorenz Curves[J]. Journal of Business and Economics Research，2011，1(1)：43-58.

[7]Kakwani N.，Podder，N.Efficient Estimation of Lorenz Curve and Associated Inequality Measures from Grouped Observations[J].Econometrics，1976，14(2)：278-291.

[8]Rasche，R. H.,Gaffney. J. Koo，A. Y.，and Obst，N. Functional Forms for Estimating the Lorenz Curve[J].Econometrics，1980，48(4)：1061-1062.

[9]Ortega p.，G. Martin，A.Fernandz，M.Ladoux，A.Garcia. A New Functional Form for Estimating Lorenz Curves[J].Review of Income and Wealth，1991，37(4)：447-452.

（责任编辑：盛桢）

F812.422

A

2095-1280(2016)06-0060-12

黄桂兰，女，南京晓庄学院商学院教师，经济学博士。