“大问题”背景下的主体学习
2016-01-31赵红婷
赵红婷
[摘 要]学生对圆形物体并不陌生,对圆的特征亦有初步感知。基于学生经验,设计有关车轮的备学问题,激活学生有关于圆的经验,并促使学生进行深度思考。“车轮为什么要做成圆形的?”这一朴素问题,直抵圆的本质属性。将圆的学习放在一个大问题背景之下,通过交流展示、质疑研讨,剖析车轮是圆形的原因和优势,从而有效突出圆“一中同长”的特质。
[关键词]准备先行 经验分享 问题研讨 反省总结 拓展延伸
[中图分类号] G623.5 [文献标识码] A [文章编号] 1007-9068(2016)01-006
【教学内容】苏教版五年级下册第85~97页的例1、例2和随后的“练一练”及练习十三的部分习题。
【教学目标】
1.使学生在观察、画图、操作等活动中感受并发现圆的有关特征,知道什么是圆的圆心、半径和直径;能借助工具画圆,能用圆规画指定大小的圆;会用圆的知识解释一些日常生活现象。
2.通过准备性活动,激活学生有关圆的经验,并让学生在活动中进一步积累认识圆的学习经验,增强空间观念。
3.使学生进一步体验图形与生活的联系,感受平面图形的学习价值,提高学生数学学习的兴趣和学好数学的自信心。
【教学重点】理解和掌握圆的特征,学会用圆规画圆的方法。
【教学难点】理解圆的有关概念,归纳圆的特征。
【教学过程】
一、备学先行——激活圆的各类经验
课前设计三个备学引导题:
1.观察车轮,试着用不同方法画出车轮外围的圆形,并说说怎样画圆更准确。
2.如果将车轮做成三角形、正方形、椭圆形等形状,会出现什么情况?请从数学的角度来分析。
3.提出三个有关圆的问题。
让学生课前独立完成备学作业,教师浏览学生的作业情况后进行教学的二度设计。
【设计意图:在生活中,圆随处可见,学生熟悉圆形物体,并对圆有初步的感知。以车轮问题作为切入点,激活了学生关于圆的经验,同时也促使学生进行深入思考。“车轮为什么要做成圆形的?”这一朴素的问题,直抵圆的本质属性。这样的备学,为学生的后续学习奠定了坚实的基础。】
二、经验分享——探索圆的主要特征
1.引出话题
师:说起圆,大家一定都不陌生,昨天我们还画了圆、剪了圆。生活中,圆随处可见,你能举两个例子吗?
生:碗、硬币、闹钟、旺仔牛奶罐……
师:生活中,人们经常把圆的东西说成是圆,区分得不太严格。比如,球、滚圆的苹果,人们常会说它们是圆的。但是,在数学上,“圆”特指平面图形。譬如,在纸上画的圆。
师(出示碗、硬币、闹钟、旺仔牛奶罐):请你找出这些物体表面的圆。此时,我们只能说这些物体的某一个面是圆。
2.备学讨论
师:最近,楠楠家买了一辆新车。有一天,他突然问我:“为什么车轮是圆形的?”我当时就愣住了,车轮当然是圆形的,这还用问吗?要说理由,还真不太好说!但这确实是一个值得研究的问题,今天我们就重点来研究这个问题。关于汽车车轮的特点,我们前几天已经进行了的备学。现在,请四人为一组讨论备学作业,每个同学都要倾听其他同学的想法,并试着解决他们的问题。组长要分好工,召集大家提炼出典型的问题!
(学生分组讨论,试着提炼出主要的发现和问题)
3.交流展示
(1)分享画车轮外形的方法
师:请一个小组代表介绍画车轮的方法。
生1:可以沿着实物的边画,也可以徒手画,或者用圆规画。
师:怎样画更准确?
生1:用圆规画更准确。
师:怎样用圆规画圆呢?
生1:捏住圆规的柄,针尖定在纸上,两脚叉开一定距离,另一只脚旋转一周,就能画出一个圆。
师(示范画圆,假装不小心失败):用圆规也不能成功画圆,问题可能出在哪里?
生1:圆规的两脚距离发生了变化或针尖移动了位置。
(学生演示用圆规画圆)
师:在画车轮外形的过程中,你能感受到车轮做成圆形的原因吗?
(2)指出圆的本质
师:如果车轮是三角形、正方形、椭圆形的,又会怎样呢?
(课件演示四种轮子的汽车行进的场景,让学生再次感悟)
生1:圆没有角,正方形、三角形有角。椭圆形虽然没有角,但一面长,一面短,不便于滚动。
生2:如果车轮做成正方形、三角形或椭圆形,车子在行进的过程中会高低不平、忽上忽下,而且前进的阻力会很大。如果车轮是圆形的,车子的轴都经过圆的中心,而圆心到圆周上的任意一点的距离都是相等的,所以在行进的过程中,车轴到地面的距离都是相等的,车子自然就能走得很平稳。
生3:由于圆上的各点到中心点(圆心)的距离相等,所以圆在滚动时,圆心在一条直线上运动,这样坐在车上的人就会觉得很平稳。由于正方形、椭圆形等边上各点到中心点的距离不一样,使得在运动过程中,中心点运动的路线不是一条直线,人坐在这样的车上就会感觉到颠簸。
(课件出示三角形、正方形、椭圆形、圆形等车轮形状图,引导学生观察这些图形,展示点到边的一些线段,让学生判断中心到边的距离是否都相等。通过对比,使学生理解圆的中心到边上任何一点的距离都相等。)
师(揭示圆心、半径的概念及字母表达式。让学生在圆中标出圆心,用字母O表示;画出一条半径,用字母r表示):可以画多少条半径?它们的长度怎样呢?为什么?
生4:可以画无数条半径,它们的长度都相等。
生5:画圆时,圆规两脚间的距离不变,所以半径都相等。
师(揭示直径的概念,并用字母d表示直径):直径可以画多少条?它们的长度怎样呢?为什么?
生6:直径有无数条,长度都相等。
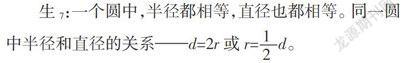
师:请从数学角度说说为什么车轮是圆的。
生8:因为从圆心到圆上任意一点的距离都相等。
生9:因为半径都相等。
师: 两千年前,伟大的思想家墨子说过:“圆,一中同长也。”请读一读这句话,说一说“一中”指的是什么,“同长”指的是什么。
生10:“一中”指的是圆心,“同长”指的是从圆心到圆上各点的距离一样长。
师:“一中同长”高度概括了圆的特征。
(3)与以前学习过的平面图形进行对比
师(出示图形,引导学生比较):圆跟我们以前学过的图形有怎样的联系?
生1:以前学过的图形都是直线图形,而圆是曲线图形,但它们都是平面图形。
【设计意图:介绍车轮画法以及由此引出的画圆过程,使学生初步感受到圆的特征。画圆时,圆规的针尖需要固定(即为定点),两脚间距离不变(即为定长)。借助车轮是三角形、正方形、椭圆形的假说,反向揭示了圆的特征。学生充分发表见解后,教师通过课件演示不同形状的车轮,让学生明白了车轮做成圆形的道理。最后,将各种车轮抽象成几何图形,对比各种图形中心到各边的距离,巧妙突出了圆“一中同长”的特征。】
三、问题研讨——凸显圆的本质属性
呈现学生备学中产生的主要问题。
问题1:怎样找到圆的直径呢?
学生动手操作,并汇报演示。
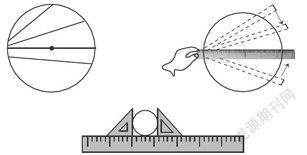
问题2:怎样找到圆的中心呢?
学生动手操作,并汇报交流。
生1:如果是圆纸片,只要对折两次就能找到圆心。
生2:如果不能对折,画两条直径,就能确定圆心,或者画一条直径,找到中点即为圆心。
师(随着学生回答,课件出示更多共性问题,如:圆的面积怎么计算?圆的周长怎么计算?圆周率是什么?……):这些问题留给大家课后思考。
【设计意图:学习总是从产生疑问开始的。小组交流过程中,一些简单问题已解决;全班研讨时,一些共性的重要问题也基本解决。这时,教师要鼓励学生将心中的疑问提出来,针对典型的问题进行研讨。随着怎样确定圆的直径、圆心等问题的解决,学生对圆的特征会有更深层次的理解。】
四、反省总结——完善圆的知识结构
师:学习了圆,你有什么收获?
生1:我知道圆有无数条半径和直径,同一个圆的半径长度都相等,直径是半径的2倍。
师:“圆,一中同长也。”这句话反过来说是“一中同长,圆也”,对吗?
师(课件出示球体):如果不限于平面内,球是不是也“一中同长”?在一个平面内,“一中同长”的就是圆,在立体空间里,“球”也是“一中同长”。数学就是这样严谨而又奇特!
【设计意图:总结能回顾所学知识,并促使知识形成体系。此处的反思,跳离了圆之本身,并随着对“一中同长,圆也”的辨析,将视野从平面的圆向立体的球延展。】
五、拓展延伸——开阔圆的知识视野
师(出示正方形车轮的自行车):车轮一定要做成圆形吗?带有正方形车轮的自行车看上去有些不切实际,但实际上它仍可以驾驶,只是它在平坦的道路上有些“大材小用”了,它更适合在像齿轮状的非平坦道路上行驶。
师(出示太极图,如下图):你见过这样的图吗?

师(出示大圆套小圆的图,图略):小圆半径是3厘米,大圆半径是几厘米?直径呢?请大家课后思考。
【设计意图:课的结束并不意味着研究的终止。教师继续追问:“车轮一定要做成圆形吗?”这一问题变换了一种思路,为学生打开了新的视野。让学生课后继续研究数学名题,带着问题走出教室,课的张力可见一斑。】
【教后反思】
这是我第二次执教“圆的认识”,跟第一次相比,思路有了很大变化。第一次执教“圆的认识”时,我紧扣“一中同长”,突出了圆的本质特征。而这次,我将学习放在了一个“大问题”背景之下,通过分析车轮是圆形的优势,突出了圆“一中同长”的特质。
源于事实的剖析。从熟悉的车轮入手,让学生在画车轮、研究车轮的过程中掌握圆的特征,真正做到了“让数学源于生活”。画车轮时,因为车轮是实物,学生想出了不同的方法,师生重点研究用圆规画圆。画圆时,定点和定长的把握,正好与圆心和半径的特点吻合。为什么车轮是圆形的?对这一司空见惯现象的追问,打开了学生思维的闸门。随着其他形状车轮的假设和演示,学生在对比中再次认识到,长方形、三角形车轮都会使汽车在行进过程中产生颠簸,从而深刻领悟到圆形车轮的优势。
基于直观的抽象。将不同形状的车轮抽象成相应图形后追问:“为什么其他形状的车轮会产生颠簸?”能够引导学生从数学的角度去思考这一问题。学生在相互启发下发现,其他图形中心到边的距离并不完全相同,而圆的中心到边的距离都相等,这是圆形车轮行驶平稳的原因,也是圆的重要特征。从直观的车轮中抽象出数学问题,通过不断追问和对比,学生成功探索了圆的特征,建构了圆的模型。数学模型的建立,基于直观又超越了直观,这样的抽象是有根基的,这样的教学也是有深度的。
高于现象的追问。“一中同长”是圆的本质特征,也是本课的灵魂,但教者并未满足于此。总结后,教师继续追问:“‘圆,一中同长也。’这句话反过来说是‘一中同长,圆也’,对吗”?学生的视角立刻从平面走向了立体。整节课虽然一直在研究圆形车轮,课尾却突然剑走回锋——出示正方形车轮的自行车。“车轮一定要做成圆形吗?”这个问题打破了学生的思维定式,使他们认识到,在某种特定情况下,正方形车轮也能平稳行走。世间并无绝对之事,新奇的问题,打开了学生思维的另一扇窗。
(责编 金 铃)
