基于RBF神经网络的机器人的路径跟踪控制

杨兴明,　李文静,　朱　建

(合肥工业大学 计算机与信息学院,安徽 合肥　230009)



基于RBF神经网络的机器人的路径跟踪控制

杨兴明,李文静,朱建

(合肥工业大学 计算机与信息学院,安徽 合肥230009)

摘要:文章针对双轮移动机器人的路径跟踪问题,提出了基于反演法的运动学控制和滑模动力学控制相结合的控制算法,运动学控制器解决位姿和跟踪速度之间的控制关系,动力学控制器解决机器人的姿态和控制电压之间的控制关系;为了减小传统运动学控制器的跟踪误差、提高路径跟踪控制的特性,采用RBF神经网络对控制器的不确定参数进行在线自适应学习。仿真结果表明,文中提出的基于RBF神经网络自适应算法比传统控制算法具有更优越的跟踪效果。

关键词:移动机器人;神经网络;滑模控制;动力学模型;姿态平衡

非完整性约束系统的路径跟踪控制具有广泛的应用价值,因而受到许多学者的高度关注。轮式机器人作为一种典型的、具有非完整性约束的机器人,其路径跟踪问题成为研究的焦点。为了实现机器人的高精度路径跟踪,许多复杂的控制方法被提出[1-10], 根据研究的模型不同分为运动学模型和动力学模型2种方式。基于运动学模型的研究主要以速度作为控制量使真实轨迹和参考轨迹之间的误差收敛到0,研究的是速度和参考轨迹之间的关系;基于动力学模型的控制器的设计反映控制电压和速度之间的关系,更适用于移动机器人的实际情况。

双轮移动机器人比三轮或四轮机器人具有更好的机动性和灵活性,体积更小,尤其是在拥挤的空间,更能体现其灵活性。然而,双轮移动机器人自身具有不稳定性,需要在路径跟踪的同时实现自身的姿态平衡,因此,本文设计了基于运动学模型的反演控制器和基于动力学模型的滑模控制器相结合的算法,并通过RBF神经网络在线自适应学习,对运动学控制器的增益进行实时修正,从而使双轮机器人在保持自身姿态平衡的同时能精确地实现路径跟踪。

1双轮移动机器人模型的建立

1.1　双轮移动机器人的运动学模型

在机器人移动的区域内建立笛卡尔坐标系(O,X,Y),选择移动机器人两驱动轮轴线的中点坐标(x,y)作为参考点,则机器人的位姿可以描述为q=[x,y,θ]T,其中θ为机器人的方向角。假设机器人运动满足纯滚动、无滑动的约束条件,则得到系统的运动学方程

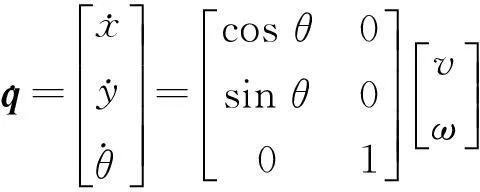
(1)

其中,v、ω分别为小车运动的速度和转弯的角速度。

1.2　双轮移动机器人的动力学模型

双轮平衡机器人的简化模型如图1所示。模型参数如下：x1、v为车底盘中心的位移和速度;δ为摆杆与竖直方向的夹角;θ、ω为机器人的方向角和角速度;Mp、mtr分别为车体质量和小轮的质量;Jtr、Jp和Jθ分别为小轮绕轴的转动惯量、车体绕电机轴的转动惯量和车体绕摆杆的转动惯量;R为车轮半径;r为车体重心到电机轴线之间的距离;D为两轮之间的距离;Km、Ke为电机的力矩系数和电机的反电动势系数;K为常系数；Ul、Ur为左、右控制电压;cr、cl为左、右电机的输出转矩。

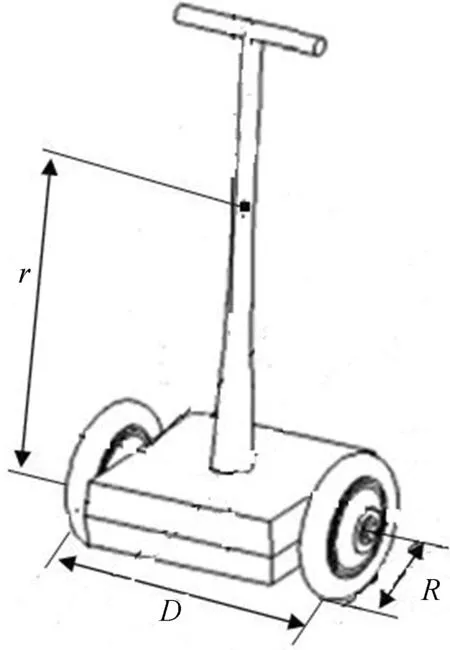
图1　双轮移动机器人的简化模型

参考文献[11],利用牛顿力学对系统建模,得到与系统状态相关的方程组为: λspan、λspan、λspan、λ的选择决定了滑模面的性能特征,本文[12]采用零极点配置的方法选取λspan=1.520,λspan=3.975 3,λspan=0.862 3,λ=1.744。其他参数如下:kspan=6,μ=10,kspan=15,

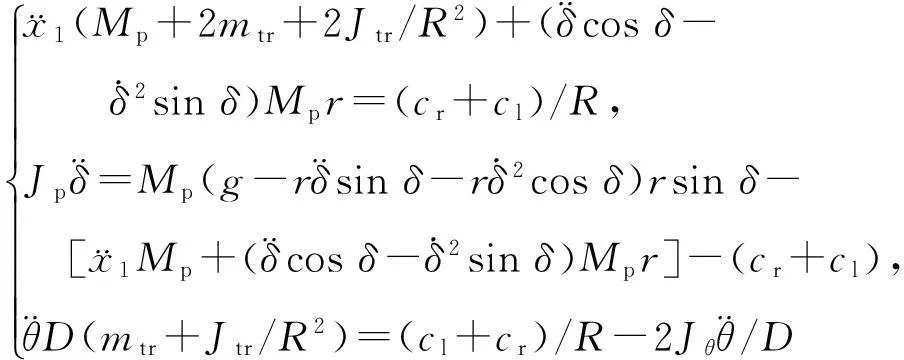
(2)

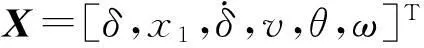
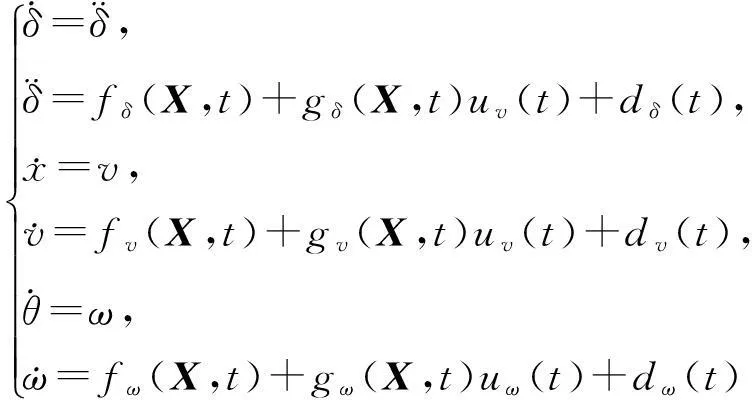
(3)

其中，uv(t)、uω(t)为控制输入;fv(X,t)、fδ(X,t)、fω(X,t)不确定部分分别为Δfv(X,t)、Δfδ(X,t)、Δfω(X,t),假设系统不确定部分上界已知,且满足|Δfv(X,t)|≤ΔFv,|Δfδ(X,t)|≤ΔFδ,|Δfω(X,t)|≤ΔFω;dv(t)、dδ(t)、dω(t)为外界干扰且满足条件|dv(t)|≤Dv,|dδ(t)|≤Dδ,|dω(t)|≤Dω。

各参数计算公式如下

2传统路径跟踪控制器的设计

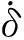
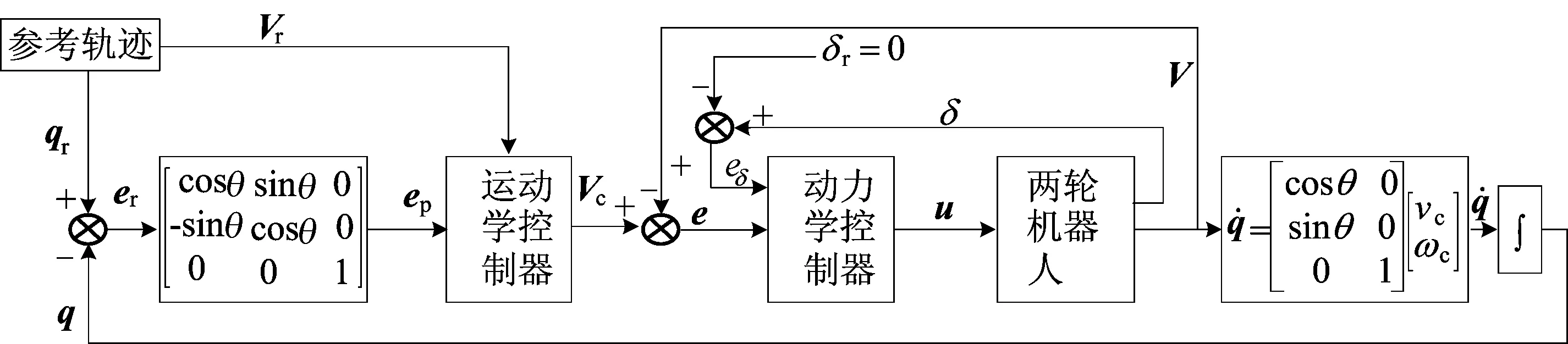
图2　双轮移动机器人的系统结构

2.1　运动学控制器的设计

基于运动学模型的反演控制器可以稳定地对移动机器人进行路径跟踪控制[10],其控制结构图参见图2。定义控制器的输入误差为:

=Teer

(4)

移动机器人跟踪速度和角速度的控制率设

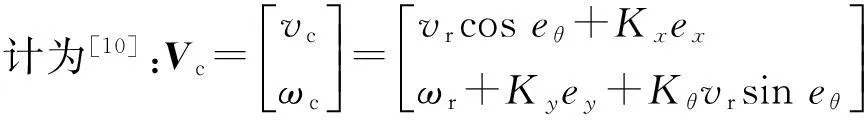
(5)

2.2　动力学控制器的设计

双轮移动机器人的动力学系统可被分为3个子系统,即平衡控制系统、速度控制系统和转弯角速度控制系统。由于平衡控制子系统和速度控制子系统由同一个控制电压uv来控制,所以具有欠驱动的特点,为了避免复杂的解耦过程,本文采用分层滑模控制器控制机器人的平衡角度和运动速度,采用传统的滑模控制器控制机器人的转弯角速度。

定义ev=vc-v,eω=ω-ωc,eδ=-δ,设计第1层滑模面为:

(6)

其中,sδ为平衡角度δ的第1层滑模面；sv为速度的第1层滑模面；sω为转弯角速度的第1层滑模面；λδ、λv、λω分别为滑模面系数。对(6)式求导,并结合(3)式可以得到:

(7)

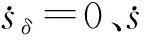
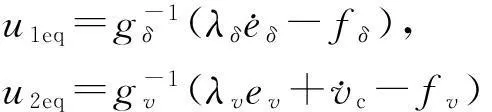
(8)

为了使得平衡角度δ和运动速度v跟踪误差都为0,根据第1层滑模面(6)式定义第2层滑模面为:

s=λsv+sδ

(9)

其中,λ为正常数。取趋近率为:

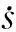
(10)

结合(7)式和(8)式可设计系统的控制律为:

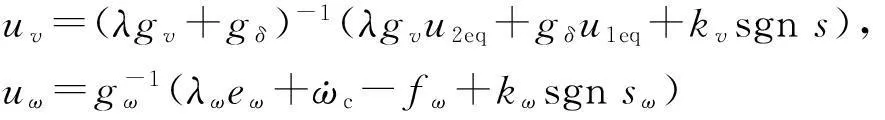
(11)

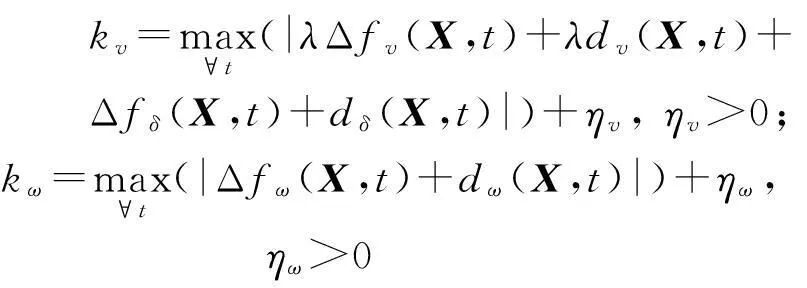
(12)

其中,kv、kω为切换项增益,是正常数。

为了证明系统的稳定性,在系统的可控范围内,构造Lyapunov函数为:

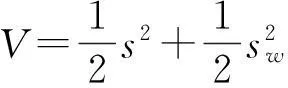
(13)

对V求导,然后结合(7)式、(8)式和(11)式可得:

s[-λΔfv(X,t)-λdv(t)-Δfδ(X,t)-dδ(t)-

ηvsgns)+sω(-Δfω(X,t)-dω(t)-ηωsgnsω]≤

s[|λΔfv(X,t)+λdv(t)+Δfδ(X,t)+dδ(t)|-

ηvsgns)+sω[|Δfω(X,t)+dω(t)|-ηωsgnsω]≤

[|λΔfv(X,t)+λdv(t)+Δfδ(X,t)+dδ(t)|-

ηv]|s|+[|Δfω(X,t)+dω(t)|-ηω)|sω|

(14)

为了抑制传统滑模控制器由于控制率的不连续性导致的抖振问题,在滑模面附近引入边界层,用脉冲函数取代不连续的符号函数。此时控制律为:

uv=(λgv+gδ)-1[λgvu2eq+gδu1eq+kvsat(s)],

(15)

脉冲函数sat(·)被定义为:

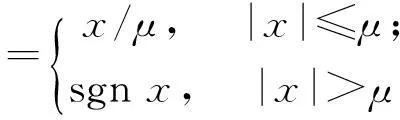
(16)

其中,μ为边界层宽度。

3自适应路径跟踪控制器的设计

基于运动学模型的反演控制器的增益Kx、Ky、Kθ的选取决定了系统的跟踪性能,为了克服传统运动学控制器中控制增益不易选择的缺点,本文采取RBF神经网络对控制器的增益进行自适应修正。

基于RBF神经网络自适应控制系统结构如图3所示。

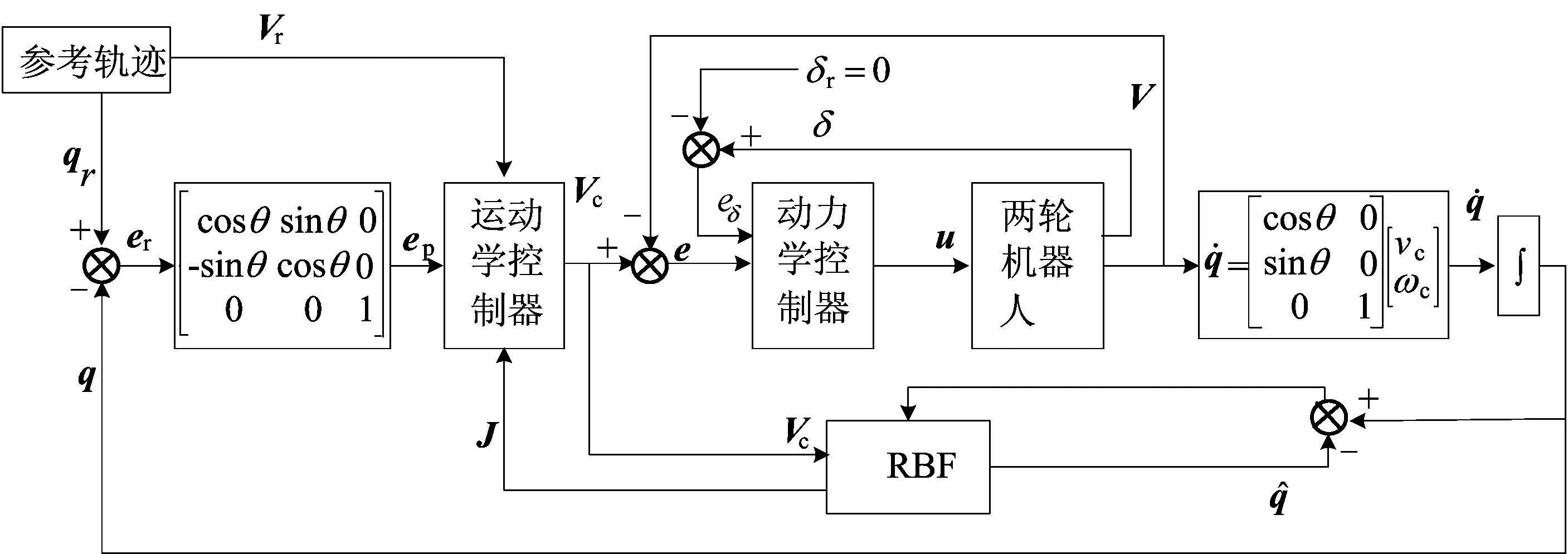
图3　基于RBF神经网络的自适应系统结构

设运动学控制器的性能函数为:

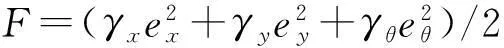
(17)

本文采用梯度下降法修正基于运动学模型的反演控制器的增益Kx、Ky、Kθ。用α=[Kx,Ky,Kθ]表示运动学控制器的增益,将(17)式的性能函数对α求导,可得:

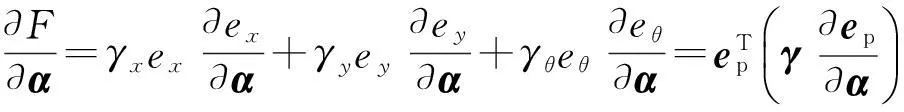
(18)

其中,γ=diag(γx,γy,γθ)。

将(4)式代入(18)式可得:

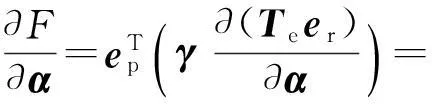
(19)

其中,∂q/∂α可改写成:

(20)

其中,∂q/∂Vc为系统的输出位姿q和输入速度Vc相关的Jacobian矩阵,定义为:

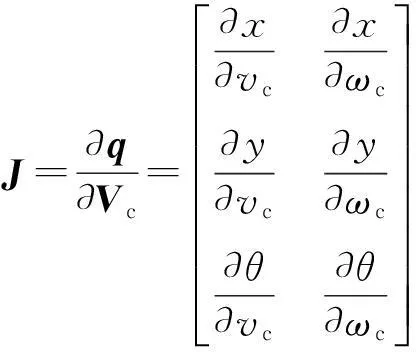
(21)

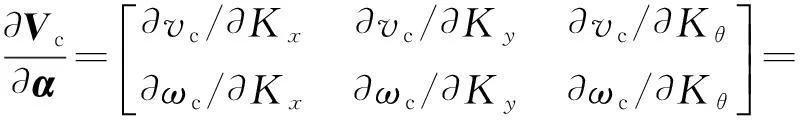
(22)

将(21)式、(22)式代入(20)式可得:

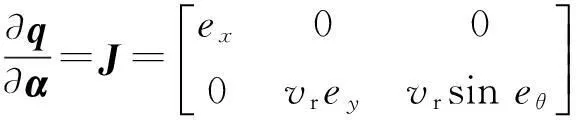
(23)

将(23)式代入(19)式可以求出∂F/∂α为:

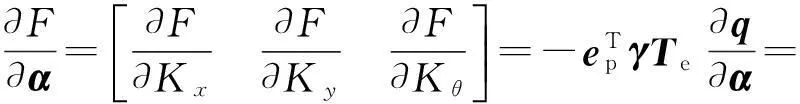
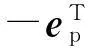
(24)

采用梯度下降法修正动力学控制器增益α的规则如下:

(25)

观察(24)式、(25)式可知,只要计算出Jacobian矩阵J的值即可计算Kx、Ky、Kθ的值,而J的值可以利用系统的精确模型求出或者利用神经网络辨识得到。由于前者需要对系统的模型参数进行精确的分析,并且要求系统参数是确定的,不适用于实际的机器人控制,所以本文采用RBF神经网络辨识计算Jacobian矩阵J的值。

RBF神经网络结构如图4所示。

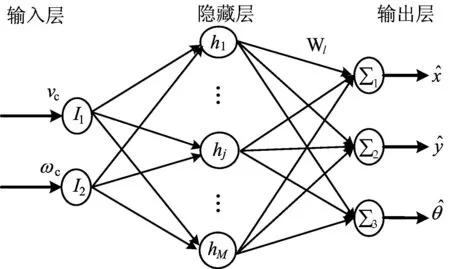
图4　RBF神经网络结构

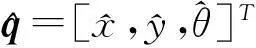
(26)

网络的第j个节点的中心矢量Clj=[clj1,clj2]T;网络的基宽向量Bl=[bl1,bl2,…,blM]T,其中blj为第l层输出对应的节点j的基宽度参数;网络的第l层输出对应的权值为:

Wl=[wl1,wl1,…,wlM]T

(27)

辨识网络的输出为:

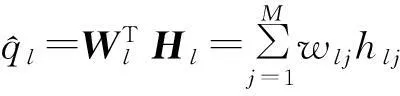
(28)

设辨识器的性能指标函数为:

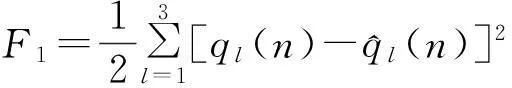
(29)

根据梯度下降法,由(29)式可以求得输出权、节点中心及节点基宽参数如下:

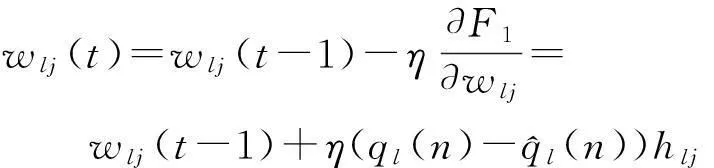
(30)

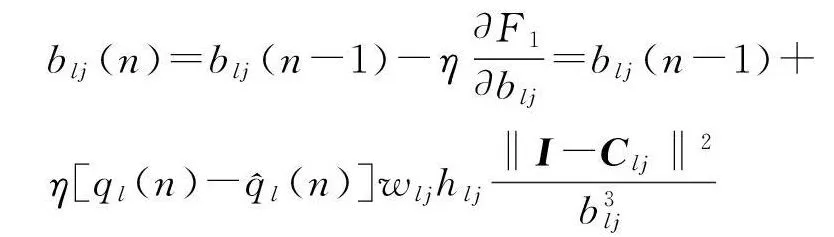
(31)

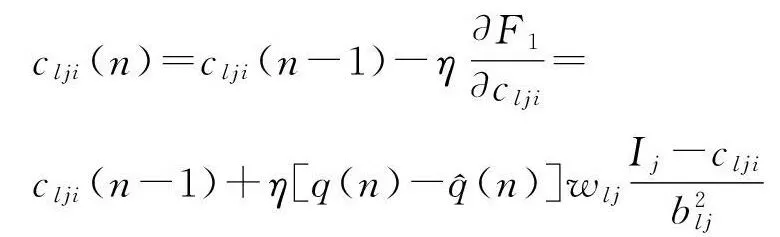
(32)

其中,η为学习因子。

对(28)式求导可得:

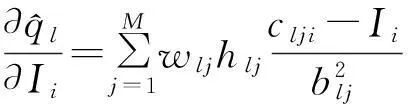
(33)

因此Jacobian矩阵J的值可以通过神经网络辨识得到，即

(34)

4仿真结果

4.1　仿真参数的选取

实际模型参数为:

Mp=16.33 kg,mtr=1.13 kg,R=0.105 m,

r=0.087 m,D=0.41 m,Km=0.050 8 N·m/V,

Ke=0.573 2 V·s/rad,Jp=0.804 kg·m2,

Jtr=0.006 23 kg·m2,Jθ=0.190 06 kg·m2。

γx=1,γy=30,γθ=10,

ηx=ηy=ηθ=0.2,η=0.25。

4.2　仿真结果及分析

(1) 圆轨迹的跟踪。假设给定的参考轨迹的圆方程为x2+y2=1,起始点为(1,0),机器人的初始位姿为(0.8,0,0)。在0～70 s的时间内,对参考曲线以0.1 m/s的速度进行跟踪仿真,结果如图5所示。

(2) 直线轨迹的跟踪。假设给定的参考轨迹是一条起始点为(0,0)、斜率为π/4的直线,机器人的初始位姿为(0.2,0,0)。在0～70 s的时间内,对参考曲线以0.1 m/s的速度进行跟踪仿真,结果如图5所示。

图5　机器人圆周运动与直线运动时的跟踪仿真结果

图5a和图5b分别为移动机器人圆和直线的跟踪曲线,可以直观地看出改进后的算法比传统算法具有更快速的跟踪参考轨迹;图5c和图5d分别为移动机器人对圆和直线跟踪误差的比较曲线,改进后的算法相对于传统算法跟踪误差更小;图5e和图6f分别为移动机器人对圆和直线跟踪时自身的平衡角度曲线,从图中可以看出,移动机器人改进后的算法能更加快速地保持自身的平衡。

上述结果表明，改进后的基于RBF神经网络的自适应算法比传统算法有更好的跟踪特性。

5结束语

本文针对双轮机器人的路径跟踪问题,把系统的控制分为运动学控制和动力学控制2个部分。其中,动力学控制采用分层滑模控制器实现对跟踪速度和姿态平衡的控制,运动学控制采用RBF神经网络对控制器的增益进行在线自适应学习。在加入系统不确定性干扰的条件下,分别用传统算法和RBF自适应算法对机器人直线轨迹和圆轨迹进行跟踪仿真,结果表明改进后的控制算法比传统的控制算法具有更好的跟踪特性。

[1]Pathak K,Franch J,Agrawal S K.Velocity and position control of a wheeled inverted pendulum by partial feedback linearization[J].IEEE Transactions on Robotics,2005,21(3):505-513.

[2]Dong W,Kuhnert K D.Robust adaptive control of nonholonomic mobile robot with parameter and nonparameter uncertainties[J].IEEE Transactions on Robotics,2005,21(2):261-266.

[3]Shen J,Sanyal A K,Chaturvedi N A,et al.Dynamics and control of a 3D pendulum[C]//43rd IEEE Conference on Decision and Control,Vol 1.IEEE,2004:323-328.

[4]Chuwa D.Sliding-mode tracking control of nonholonomic wheeled mobile robots in polar coordinates[J].IEEE Transactions on Control Systems Technology,2004,12(4):637-644.

[5]Buccieri D,Perritaz D,Mullhaupt P,et al.Velocity-scheduling control for a unicycle mobile robot:theory and experiments[J].IEEE Transactions on Robotics,2009,25(2):451-458.

[6]杨芳,王朝立.不确定非完整移动机器人的轨迹跟踪控制[J].控制工程,2012,19 (2):258-261.

[7]秦勇,闫继宏,王晓宇.两轮自平衡机器人运动控制研究[J].哈尔滨工业大学学报,2008,40(5):721-726.

[8]Yue Liyong,Xie Wei.An Adaptive Tracking Method for Non-holonomic Wheeled Mobile Robots[C]//Proceedings of the 26th Chinese Control Conference,Zhangjiajie,Hunan,China,2007:801-805.

[9]Martins N A,Bertol D,Lombardi W,et al.Trajectory tracking of a nonholonomic mobile robot with parametric and nonparametric uncertainties:a proposed neural control[C]//Proceedings of the 16th Mediterranean Conference on Control and Automation.IEEE,2008:315-320.

[10]Kanayama Y,Kimura Y,Miyazaki F,et al.A stable tracking control method for an autonomous mobile robot[C]//Proceedings of the IEEE Conference on Robotics Automation.IEEE,1990:384—389.

[11]陈星,魏衡华,张玉斌.二轮行走倒立摆系统的建模与鲁棒方差控制[J].计算机仿真,2006,23(3):263-266.

[12]Utkin V.Sliding mode control design based on Ackermann’s formula[J].IEEE Transactions on Automatic Control,1998,43(2):234-237.

(责任编辑胡亚敏)

韩江洪(1954-),男,安徽泾县人,合肥工业大学教授,博士生导师.

Path tracking control of mobile robot via RBF neural network

YANG Xing-ming,LI Wen-jing, ZHU Jian

(School of Computer and Information, Hefei University of Technology, Hefei 230009, China)

Abstract:This paper presents an algorithm combining the kinematics controller designed by backstepping method and the dynamics controller designed by the sliding mode control for two wheeled mobile robot path tracking. The kinematics controller is used to solve the control relationship between the posture and tracking speed, and the dynamics controller is used to solve the control relationship between the attitude and the control voltage of the robot. In order to reduce the tracking error of the traditional kinematics controller and improve the characteristics of path tracking control, the RBF neural network adaptive online learning is used for uncertain parameters of the controller. The simulation results show that the proposed adaptive algorithm based on RBF neural network has better tracking performance than the traditional control algorithm.

Key words:mobile robot; neural network; sliding mode control; dynamics model; posture balance

doi:10.3969/j.issn.1003-5060.2015.11.009

作者简介：彭浩(1984-),男,安徽合肥人,合肥工业大学博士生;

基金项目：国家自然科学基金资助项目(61370088;61202096)和安徽省自然科学基金资助项目(1208085QF118)

收稿日期：2014-11-13；修回日期：2014-12-15

中图分类号:TP273

文献标识码：A

文章编号：1003-5060(2015)11-1477-07