模态跳跃现象对振动分析的影响研究

张　淼,　于　澜,　鞠　伟

(1.长春工程学院 理学院,吉林 长春　130012; 2.中国第一汽车股份有限公司 技术中心,吉林 长春　130011)



模态跳跃现象对振动分析的影响研究

张淼1,于澜1,鞠伟2

(1.长春工程学院 理学院,吉林 长春130012; 2.中国第一汽车股份有限公司 技术中心,吉林 长春130011)

摘要:文章揭示了模态的跳跃现象对振动分析的影响,并给出了一种新的结构优化设计的方法。首先通过特征分析获得了频率密集程度不同的3种密频状态系统,并给出了接近密频与接近重频系统的概念,同时指出密、重频系统存在模态跳跃现象;其次对设计参数取不同值时所对应的多个密、重频系统,利用频响函数矩阵计算结构在简谐激励下的动力响应;最后通过响应曲线的对比分析,得出有关模态跳跃现象对振动分析影响的结论。

关键词:振动分析;密集频率;模态跳跃;动力响应;结构优化

在实际工程中,很多结构由于自身原因或外界因素的影响,当结构参数发生微小的变化时,就可能引起结构的部分模态信息出现急剧变化,即产生模态跳跃现象,这种现象最早是美国国家航天局(NASA)的专家在弹性薄板构件的瞬态屈曲试验过程中发现的,随后一些学者做了后续的研究[1-2]。近年来,这种现象在力学、土木工程和航空航天等领域逐渐得到关注,而研究对象也由柔性板等简单构件逐渐向更复杂结构转变[3-4],同时在密、重频系统的研究过程中[5-6],很多研究人员发现频率密集极可能会引起模态跳跃现象的发生[7-8],但这种现象会对结构产生何种影响，目前相关研究较少。

为了使用模态分析法来求解结构的精确响应,必须获得其固有频率及模态信息,这样解耦的模态方程才可以很容易地进行积分。模态分析法非常适用于结构动力学问题的求解,例如在地震载荷的作用下,只需要利用结构的几个低阶模态,就可以近似得到具有较好精度的结构动力响应结果,况且由于高阶模态通常对系统的实际响应影响有限,同时有限元法得到的高阶模态又与实际相差很大,因此,从这个意义上讲,求解高阶模态的意义不大,但低阶模态是必需的。从上述分析可以看出模态是计算响应的基础,模态跳跃现象会对结构的动力响应产生影响。

随着静力条件下的结构优化设计理论的日益成熟及工程设计要求的逐步提高,结构动力学优化设计受到越来越多的关注,结构动力学优化包括结构动力学特性优化和动态响应优化2类,相比而言,由于结构动力响应的控制属于多目标、多约束优化的数学模型,因而更为复杂、难度更大[9-10]。本文结合一个二自由度阻尼系统的算例,分析模态的跳跃现象对振动响应的影响,并提出一种新的结构优化设计的方法。即首先分析固有频率随设计参数变化而产生变化的规律,然后研究当固有频率为密集或重复状态时,相应系统的模态随之发生跳跃变化的规律,最后利用稳态响应来对比和分析这些系统的振动特性,从而揭示模态发生跳跃时系统响应的变化规律。这样就可以实现通过讨论结构动力响应与设计参数之间的关系,来确定在某种动力响应要求下的设计参数的最优值,从而获得最优的设计方案。

1模态跳跃现象及其原因

N自由度的线性离散振动系统的自由振动方程为:

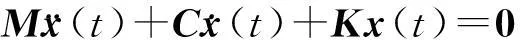
(1)

其中,M、C、K分别为系统的质量、阻尼和刚度矩阵。其相应的强迫振动方程为:

(2)

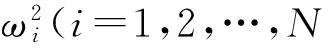
(3)

设每个实模态的规范化常数为ai,即

(4)

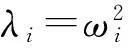
(K-λiM)φi=0

(5)

实际上特征方程(5)式是关于矩阵M和K的广义特征问题。λi称为固有频率,与之对应的规范化后的无阻尼模态φi又可称为振型或实模态。

当结构参数发生变化时,研究系统的固有频率和模态随之发生变化的规律,既可以使用特征灵敏度作为参考指标,也可以通过直接研究特征曲线来完成,数据处理技术在这2种方法的应用过程中的有效性及可靠性参见文献[11-12]。本文将使用该方法来实现结构的固有频率分析及实模态分析。

1.1　固有频率分析

考虑一个二自由度的阻尼系统,如图1所示。

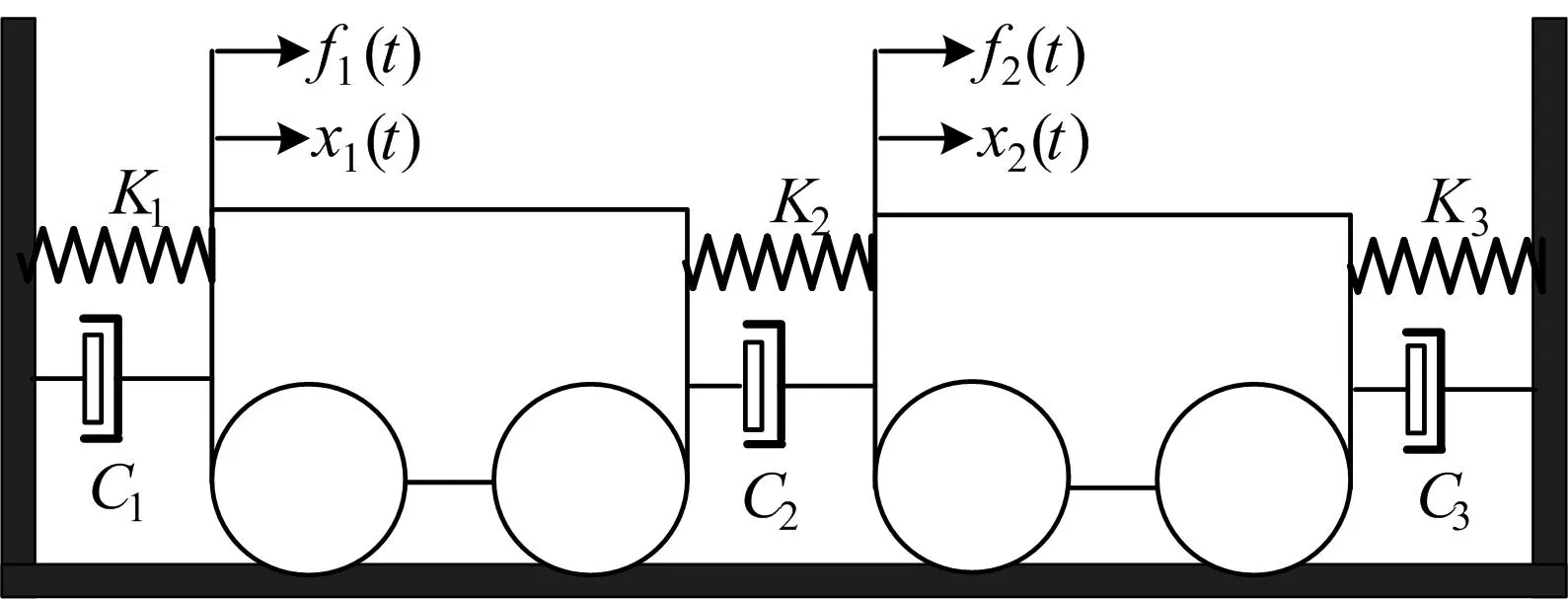
图1　二自由度阻尼振动系统

其中,质量、刚度和阻尼矩阵分别为:

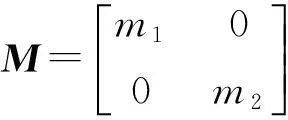
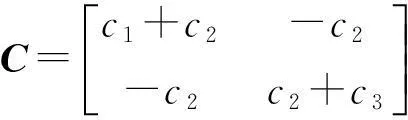
(5)式为其无阻尼特征方程,λi(i=1,2)为此系统的特征值,φi(i=1,2)为此系统的特征向量。解得其特征值为:

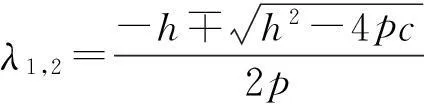
(6)

其中,p=m1m2;h=-(k1+k2)m2-(k3+k2)m1;c=k1k2+k1k3+k3k2。

令m1=m2=1,k3=1,而取设计参数为k1,其变化区间取为0.6～1.4,分别在k2=0.05,k2=0.005和k2=0.000 5 这3种情况下,利用(6)式得到λ1和λ2关于设计参数k1的关系图,并获得了3个频率密集程度不同的密频状态系统,如图2所示。

由图2可知,对于k2取不同值的3种情况下,系统均在k1=1处发生2个特征值λ1与λ2接近的现象,此时相应的系统称为密频系统,而其余情况下的对应系统视为接近密频系统(或单频系统)。由图2c可知,第3种密频状态中,当k2=0.000 5时,系统在k1=1处出现了重频现象,即2个特征值相等,此时相应的系统称为重频系统,其余情况下所对应的系统视为接近重频系统 (或单频系统)。

图2　特征值关于设计参数k1的关系曲线

由图2可知,k2取值越小,在k1=1处所生成的系统密频程度越高,甚至出现了重频现象。

1.2　实模态分析

相应地,按(4)式规范化后的特征向量为:

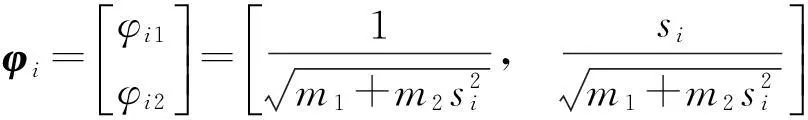
i=1,2

(7)

与固有频率分析的过程类似,令m1=m2=1,k3=1,而取设计参数为k1,其变化区间取为0.6～1.4,分别研究在k2=0.05,k2=0.005和k2=0.000 5时由(7)式得到的φ1和φ2与设计参数k1的关系后发现,当k2从0.05向0.000 5变化时,φ1和φ2均在k1=1处两侧发生了急转和跳跃,且其变化程度越来越剧烈,其中最为剧烈的情形如图3所示。这说明φ1与φ2的不稳定性均发生在密频点k1=1处两侧,系统的密频程度越高,系统模态的跳跃性越强,换言之,密频的发生与模态跳跃现象呈现出高度的相关性。

图3　k2=0.000 5时,φ1、φ2与k1的关系

为了进一步说明这种现象,绘制出φ1和φ2的第1维分量关于设计参数k1的一阶导数图(或称为一阶灵敏度图),如图4所示。事实上,它们的第2维分量关于设计参数k1的一阶导数也大体相同,只是符号相反。

由图4可知,φ1与φ2在k1∈[0.6,0.9]∪[1.1,1.4]时的变化率几乎为0,说明此时模态随设计参数的变化不大,较为稳定,但在k1∈[0.9,1.1]时,特别是在k1=1附近,φ1与φ2变化率发生了较大的波动,并且k2的值越小,变化率的变化幅度越大,这显示出模态在这个范围内发生了一定程度的跳跃,说明密、重频对灵敏度分析的影响较大,模态的跳跃现象确实是存在的,而用灵敏度来展示模态的跳跃性较为直观有效。

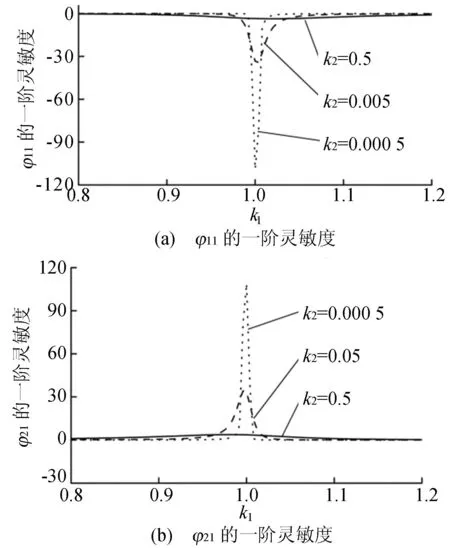
图4　k2取不同值时,φ11与φ21关于设计参数k1的一阶灵敏度

2模态跳跃对动响应分析的影响

根据上述分析可知,由于设计参数变化所产生的密频系统,其密频程度越高,模态的跳跃性就越强,下面研究和比较模态的跳跃性对这些系统的动力响应分析的影响。

2.1　第1种密频状态下的系统响应

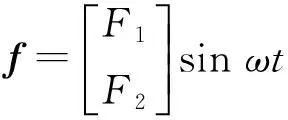
对于设计参数k2=0.05,k1分别取0.6、0.8、1.2、1.4时所形成的几种接近密频的系统,同样使用上述方法便可获得与图5相同的简谐激励下的稳态响应曲线。但是为了便于比较,只是给出时间在0～2.5 s内的响应曲线,如图6所示,其他部分的曲线与图5a的情况类似都是呈周期性变化的,下文与此情况类似的部分不再赘述。

由图4可知,当k2=0.05时,只有设计参数k1在密频点处时,相应的密频系统的实模态灵敏度最大,即模态的跳跃性最强,但由图5、图6对比可知,密频系统的响应幅度较其他接近密频系统的响应而言却最小,这说明密频系统相对稳定。

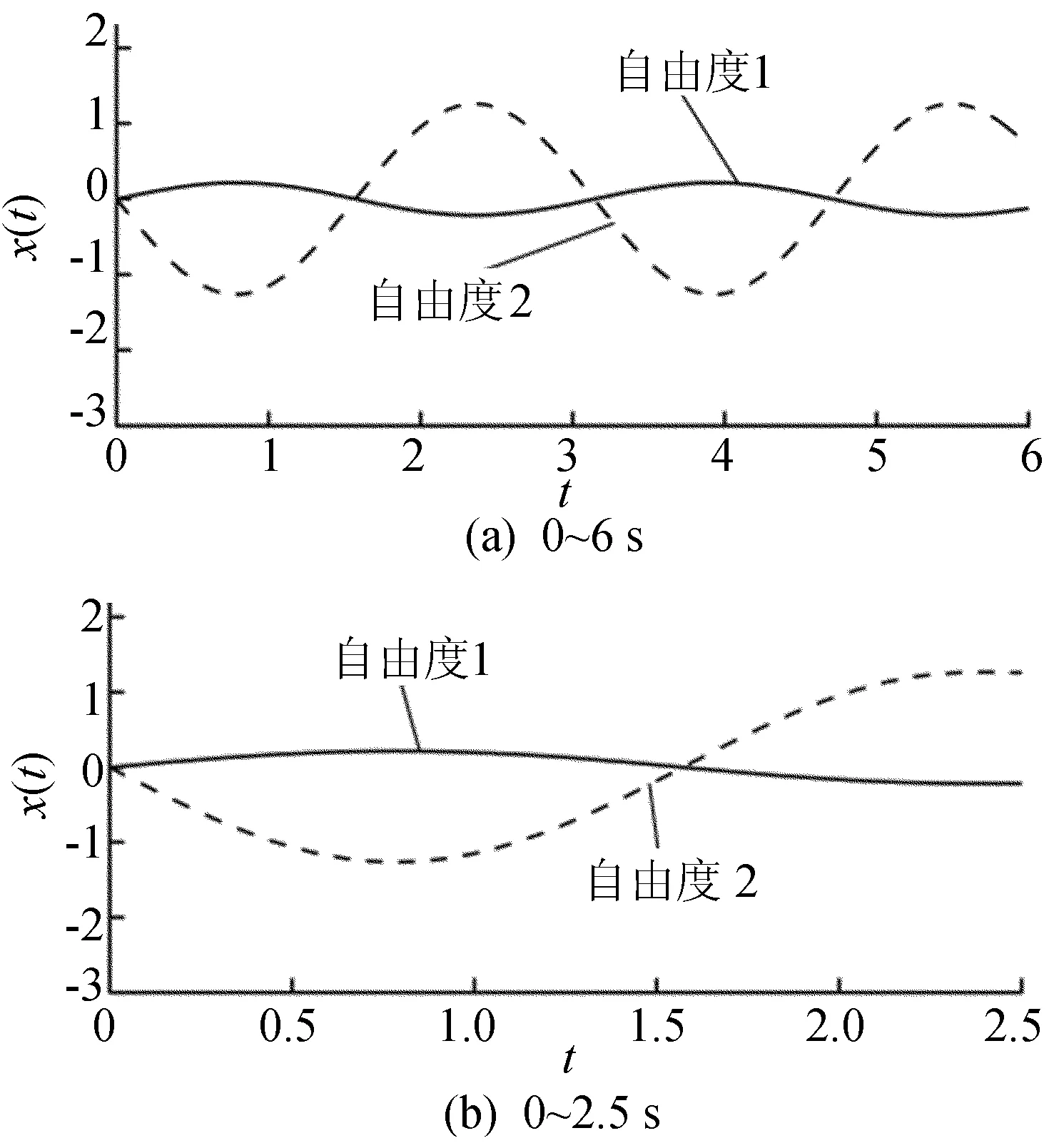
图5　k1=1，k2=0.05时的密频系统响应曲线

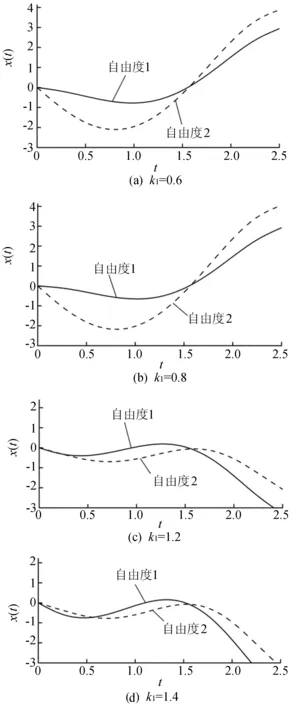
图6　k2=0.05,k1 取不同值时接近密频的系统响应曲线

2.2　第2种密频状态下的系统响应

图7　k1=1,k2=0.005时的密频系统响应曲线

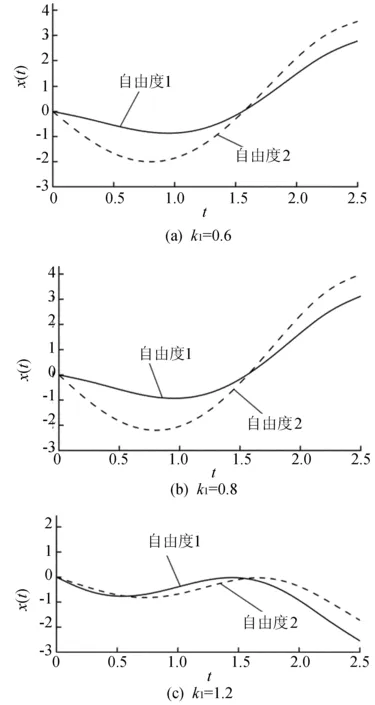
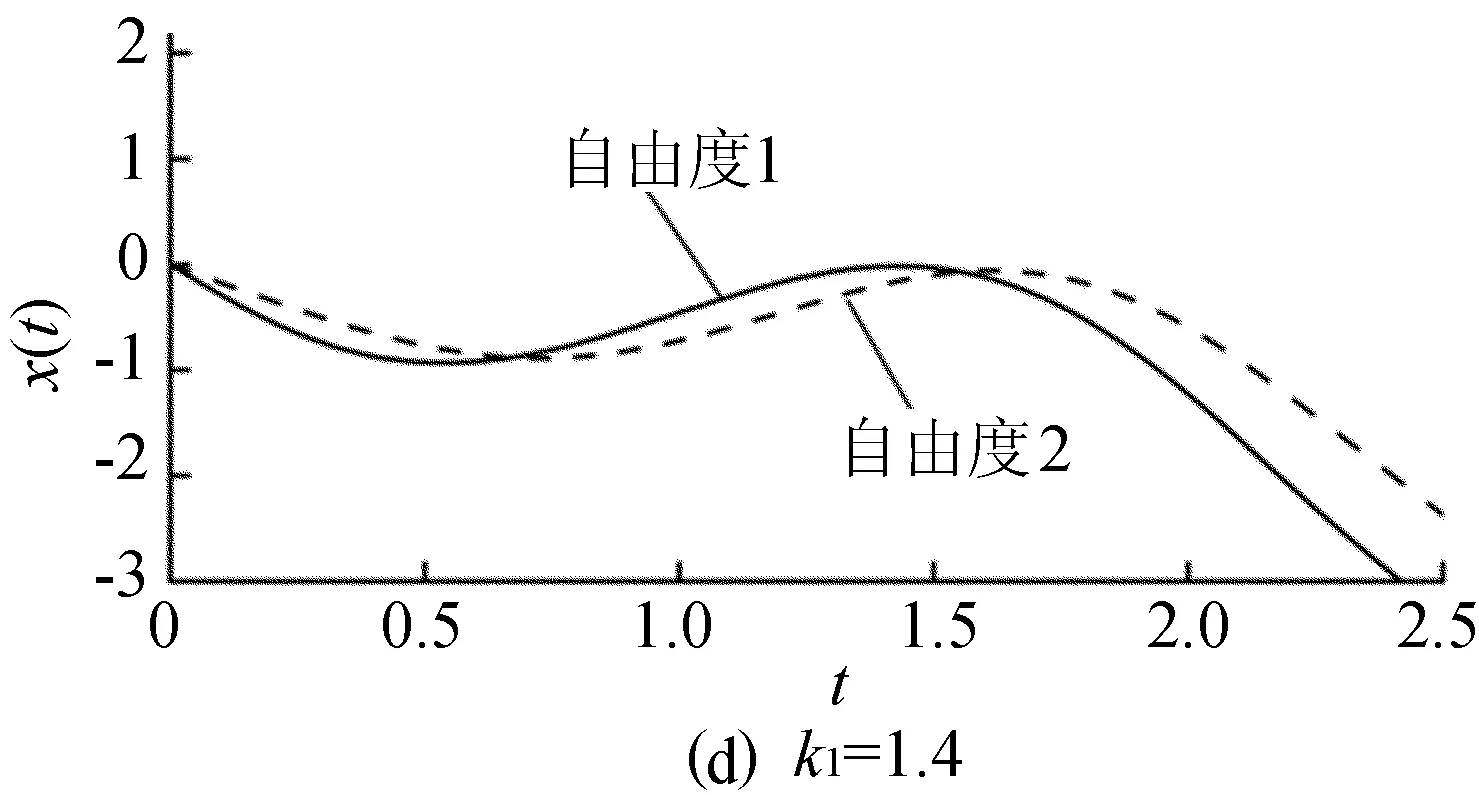
图8　k2=0.005,k1 取不同值时接近密频的系统响应曲线

由图4可知,当k2=0.005时,只有设计参数k1在密频点处时,相应的密频系统的实模态灵敏度最大,即模态的跳跃性最强,但通过图7、图8的对比,并结合固有频率图2b可知,密频系统的响应幅度最小,这也说明密频系统相对稳定。

2.3　第3种密频状态下的系统响应

由于图2c中呈现出了重频状态,其响应问题最值得关注。采用与2.1及2.2中同样的处理方法得到重频状态及接近重频状态的结构动力响应曲线,如图9、图10所示。

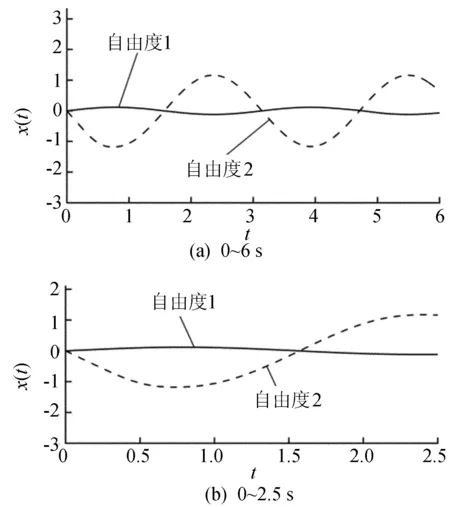
图9　k1=1,k2=0.000 5时的重频系统响应曲线

图10　k2=0.000 5,k1 取不同值时接近重频的系统响应曲线

由实模态分析图4可知,当k2=0.000 5,只有当设计参数k1在重频点处,相应的重频系统的模态跳跃性最强,再通过图9和图10对比,并结合固有频率图2c分析可知,此时的重频系统的响应幅度却最小,说明重频系统最稳定。

图6、图8、图10分别对应于图2a、图2b、 图2c中设计参数分别取不同值时多个接近密频的系统响应曲线,通过横向比较可知,振动状态区别不是很大。而图5、图7、图9所对应的系统分别对应于图2a、图2b、 图2c中设计参数k1取最密频点时,而k2分别取为0.05、0.005及0.000 5所形成的3个系统,其密频程度随k2减少而增强,再由图4可知,其模态的跳跃程度也随之增强,因此同时比较这3个系统响应显得尤其必要。从图5、图7、图9中难以发现细微差别,因此采用响应数据来进行说明,见表1、表2所列。

表1　k1=1时系统的第1自由度的响应值x1(t)

表2　k1=1时系统的第2自由度的响应值x2(t)

由表1、表2可知,在各时间点处,频率越密集的系统,其2个自由度的响应幅度越小,而重频系统的响应幅度最小,这说明重频系统更为稳定。

从以上研究中可以得出结构优化设计中的一个重要的结果,即一个设计参数k2取所需的值0.05、0.005、0.000 5时,另一个设计参数k1只有取1时,系统的响应幅度最小,这就是以动力响应为优化目标的最优设计方案。

将上述的研究过程推广到一般情况,便得到了一种新的结构优化设计方法。即在结构设计的初始阶段,对于某个重要的设计参数,可以在与其相关度较大的某个设计参数取某些特殊值的前提下,在其可行域内计算结构的固有频率及实模态的灵敏度,进而分析它们随设计参数变化而变化的特点。然后通过计算相应结构的响应,分析其稳定性。最后确定满足某种动力响应要求的该设计参数的最优值，从而获得最优的设计方案。

3结论

本文针对由设计参数变化所产生的密频及重频、接近密频及接近重频等多个系统,施加相同的简谐激励后,对其产生的稳态响应进行分析,可得到如下结论:密频或重频现象的发生，对灵敏度分

析所带来的影响是巨大的，但对结构动力响应分析的影响并不大；密频程度越高时，模态的跳跃性越强，而系统响应的幅度却越小；重频系统是所有振动系统中最稳定的。

同时,本文给出了一种基于动力响应的结构设计的新的优化方案。

[参考文献]

[1]Eduard R,Charle C R,Francis A B.On the solution of mode jumping phenomena in thin-walled shell structures [J].Computer Methods in Applied Mechanics and Engineering,1996,136:59-92.

[2]Everall P R,Hunt G W.Mode jumping in the buckling of structs and plates:a comparatives study [J].International Journal of Non-Linear Mechanics,2000,35:1067-1079.

[3]于岩磊,高维成,刘伟,等.密集模态结构模态跃迁分析的简化摄动法[J].工程力学,2012,29(3):33-39.

[4]蒋友宝,冯健,孟少平.结构损伤识别中模态跃迁的研究[J].工程力学,2006,23(6):35-40,76.

[5]张淼,于澜,鞠伟.基于松驰技术的重频密频结构模态灵敏度分析[J].合肥工业大学学报:自然科学版,2012,35(12):1605-1609.

[6]张淼,于澜,鞠伟.重频系统的频率灵敏度分析算法研究[J].华南师范大学学报:自然科学版,2014,46(3):39-43.

[7]刘潇翔,胡军.包含密集模态的空间结构的模糊主动振动控制[J].空间控制技术与应用,2010,36(4):18-24.

[8]刘利军,樊江玲,张志谊,等.密频系统模态参数辩识及其振动控制的研究进展[J].振动与冲击,2007,26(4):109-115.

[9]谭平,卜国雄,刘红军,等.带TMD结构的随机地震响应分析的新方法[J].北京理工大学学报,2010,30(4):390-394.

[10]陈臻林.大型结构动力响应的状态方程的Krylov精细时程积分法[J].力学与实践,2010,32(2):76-81.

[11]张淼.数值技术在结构特征值分析中的应用研究[J].长春理工大学学报:自然科学版,2014,37(2):124-127.

[12]张淼.讨论密频结构实模态参数的特征曲线法[J].长春师范学院学报:自然科学版,2014,33(2):1-4.

[13]张淼,于澜,鞠伟.基于频响函数矩阵计算阻尼系统动力响应的新方法[J].振动与冲击,2014,33(4):161-166.

(责任编辑张镅)

Research on the effect of modal jumping phenomenon on vibration analysis

ZHANG Miao1,YU Lan1,JU Wei2

(1.School of Science, Changchun Institute of Technology, Changchun 130012, China; 2.R&D Center, China FAW Group Corporation, Changchun 130011, China)

Abstract:The effect of modal jumping phenomenon on vibration analysis was discussed, and a new method of structural optimization design was proposed. Firstly, three kinds of closed-frequency systems with different closed extents were obtained by eigenproblem analysis, and the concepts of quasi-closed-frequency system and quasi-multiple-frequency system were defined. It was stated that the modal jumping phenomena exist exactly in closed-frequency and multiple-frequency systems. Secondly, in terms of several closed-frequency and multiple-frequency systems corresponding to different values of design parameters, the dynamic responses of them under simple harmonic excitation were computed based on frequency response matrix. Finally, some conclusions about the effect of modal jumping phenomenon on vibration analysis were drawn through contrasting different response curves obtained.

Key words:vibration analysis; closed frequency; modal jumping; dynamic response; structural optimization

doi:10.3969/j.issn.1003-5060.2015.11.024 10.3969/j.issn.1003-5060.2015.11.018

作者简介：曾伟(1980-),女,四川德阳人,合肥工业大学副教授. 汪莲(1959-),安徽宣城人,合肥工业大学副教授,硕士生导师.

基金项目：国家自然科学青年基金资助项目(71201044)；安徽省级优秀青年人才基金重点资助项目(2013SQRW003ZD)和中央高校基本科研业务费专项资金资助项目(J2014HGXJ0069；2015HGZX0021) 安徽省交通科技进步计划资助项目(2014-35)

收稿日期：2014-11-13；修回日期：2015-01-05 2014-11-13；修回日期：2014-12-24

中图分类号:O321

文献标识码：A

文章编号：1003-5060(2015)11-1524-07